2. 船舶数据技术与支撑软件湖北省工程研究中心,湖北 武汉 430074;
3. 高新船舶与深海开发装备协同创新中心,上海 200240;
4. 沪东中华造船(集团)有限公司开发研究所,上海 200129;
5. 九江职业技术学院 船舶与海洋工程技术研究所,江西 九江 332000;
6. 武汉第二船舶设计研究所 湖北 武汉 430064
2. Hubei Engineering Research Center of Ship Data Technology and Support Software, Wuhan 430074, China;
3. Collaborative Innovation Center for High-tech Ships and Deep-sea Development Equipment, Shanghai 200240, China;
4. Development Research Institute in Hudong Zhonghua Shipbuilding (Group) Co. Ltd., Shanghai 200240, China;
5. Institute of Ship and Marine Engineering Technology in Jiujiang Polytechnic, Jiujiang 332000, China;
6. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
螺旋桨作为常规船舶的动力源泉,其性能研究是船舶水动力研究中的重要部分。随着科学技术的发展螺旋桨性能研究的方法也越来越多样化,其中CFD数值仿真是继理论分析和模型试验后最为重要的手段之一。螺旋桨水动力研究方面,何惠明等[1]在波浪条件进行船舶的自航模拟试验,获得了该船在不同波浪下的自航因子。Carrica P M等[2]使用CFDShip-lowa v4对KVLCC1,DTMB5613和KCS三艘船进行自航数值模拟,采用了DES湍流模型和动网格技术,模拟结果与试验结果吻合较好。Alejandro M.Castro等[3]对KCS船进行实尺度敞水试验,根据试验结果并结合阻力、自航的数值模拟数据,最终得到了船舶的自航因子。郭春雨等[4]以某75 000 t 散货船为研究对象,研究CFD 仿真模拟自航试验及数据处理方法,该方法针对傅汝德数小于0.2的船舶可实现准确预报。沈兴荣等[5]使用CFD数值仿真方法对4 000 TEU标准集装箱船进行分析,进一步说明数值计算在集装箱船的自航计算上具备可行性和准确性。
采用RANS方法,以KCS船和KP505桨为对象,进行船舶自航数值仿真。在验证数值仿真可靠性的基础上更改螺旋桨盘面比,发现不同盘面比螺旋桨作用下船体阻力变化不显著,推力减额变化不显著,总推进效率随着桨盘面比增大减小显著。
1 数值计算原理船舶外流场求解实质是对连续性方程和N-S方程[6]进行求解,包含质量守恒和动量守恒。其中流体的连续性方程和N-S方程分别如下:
| $ \nabla \cdot \mathit{u}=0 \text{,}$ | (1) |
| $ \frac{\partial {u}_{i}}{\partial t}+\frac{\partial \left({u}_{i}{u}_{j}\right)}{\partial {x}_{j}}=-\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+\nu \frac{\partial }{\partial {x}_{j}}\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right) \text{。}$ | (2) |
式中:
湍流中速度变化无规律,基于统计学原理,将速度分解为时均速度和脉动速度,其表达式如下:
| $ 22{u}_{i}=\overline{{u}_{i}}+{u}_{i}\mathrm{\text{′}} \text{,}$ | (3) |
式中,
| $ \frac{\partial {u}_{i}}{\partial t}+\frac{\partial \left({u}_{i}{u}_{j}\right)}{\partial {x}_{j}}=-\frac{1}{\rho }\frac{\partial \rho }{\partial {x}_{i}}+\nu \frac{\partial }{\partial {x}_{j}}\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right)+\frac{1}{\rho }\frac{\partial }{\partial {x}_{j}}(-\overline{{u}_{i}\mathrm{\text{′}}{u}_{j}\mathrm{\text{′}}}) \text{。}$ | (4) |
以KCS船模和KP505桨为对象,采用CFD软件STAR-CCM+进行数值仿真研究,由文献[7]可知相关试验结果数据。船舶主要参数如表1所示,三维模型如图1和图2所示。
|
|
表 1 KCS集装箱船主要参数 Tab.1 Main parameters of KCS container ship |

|
图 1 KCS集装箱船模型 Fig. 1 KCS container ship model |

|
图 2 KP505桨模型 Fig. 2 KP505 propeller model |
参考文献[8-9],计算域大小为4L×4L×3L,其中L为船长,具体域的范围及条件设定为:来流方向距船首1L,去流边界距离船尾2L,侧面和底部距离船舶中心2L,底部距离船舶中心1L。在螺旋桨周围设置旋转域,其大小为1.25倍桨径。
网格基础尺寸一般取船长的1/20到1/50,依照本模型尺度基础尺寸取0.14 m。网格模型选择表面重构对网格曲率和兼容性进行优化,采用切割体网格单元生成器控制不同方向的网格增长率。根据文献[10-11],生成边界层网格时控制

|
图 3 自航计算旋转域网格 Fig. 3 Self-propelled computing rotation domain grid |
在物理模型的选择上,选用K-Epsilon湍流、VOF波、三维、两层全y+壁面处理、欧拉多相、流体域体积(VOF)、重力和隐式不定常。各计算的入口均设置为速度入口并给定速度,两侧的计算域则定义为对称平面,出口设置为压力出口,其中船体和螺旋桨定义为不可滑移表面。
3 结果分析 3.1 KP505桨计算结果根据KCS的大量模型试验数据在数值模拟开始前对其自航点进行预估,确定计算3个转速分别为9.3 r/s、9.5 r/s和9.7 r/s,按照上述转速计算模型阻力RT、螺旋桨推力T和扭矩Q,结果如表2所示。
|
|
表 2 不同转速船桨受力结果 Tab.2 Force results of propellers at different speeds |
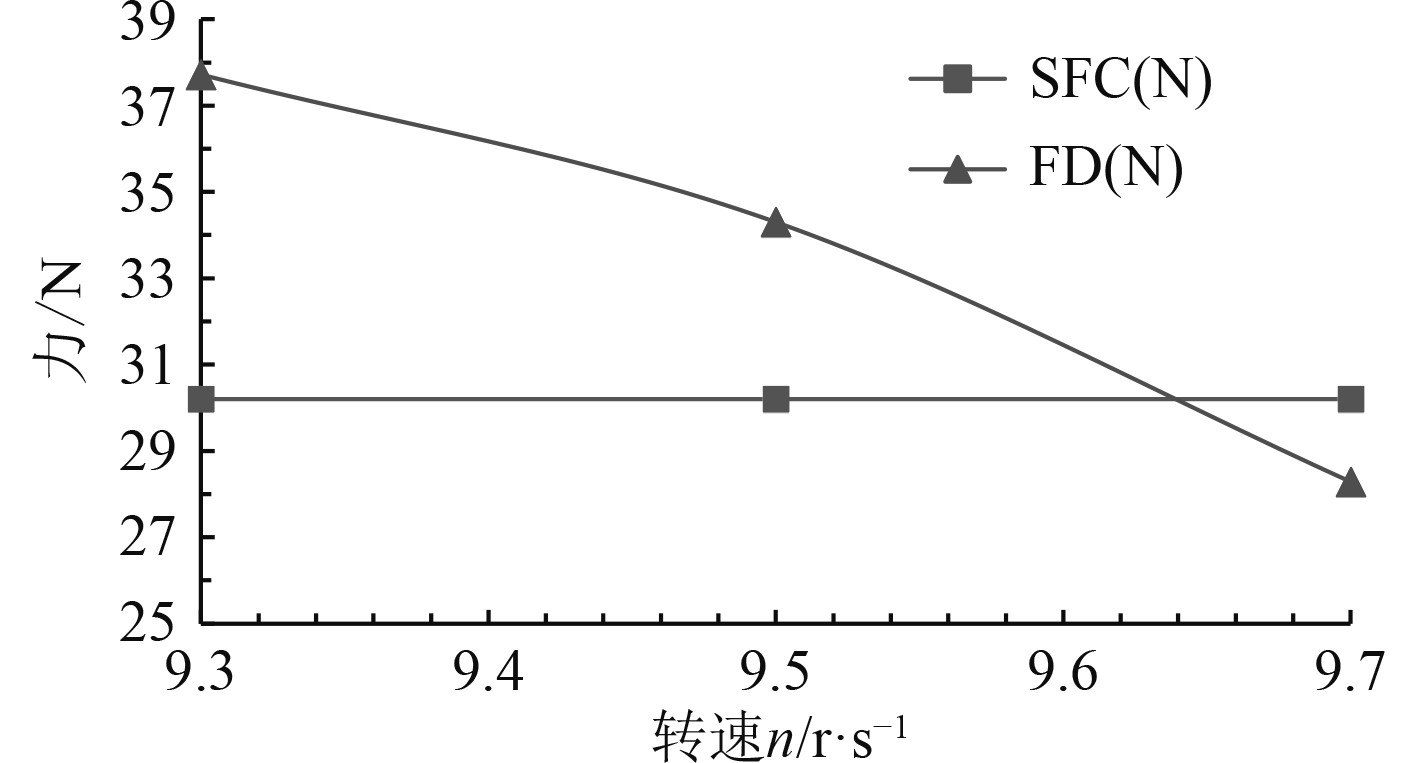
以转速为横坐标强制力FD为纵坐标绘制曲线,如图4所示。对强制力进行插值得自航点转速n = 9.64 r/s,其中
|
|
表 3 自航模拟与实验结果对比1 Tab.3 Comparison of self-propelled simulation and experimental results 1 |
|
图 4 自航曲线 Fig. 4 Self-propelled curve |
|
|
表 4 自航模拟与实验结果对比2 Tab.4 Comparison of self-propelled simulation and experimental results 2 |
分析结果可知,计算值与已有试验结果相比误差较小,其中自航状态船体总阻力误差不到1%,自航因子误差均控制在5%以内,可在工程上满足需求。
3.2 不同盘面比桨计算结果按照上述设置方案,将原桨型盘面比AD/A0更改为0.6和1.1,按照同样处理方法得到不同盘面比桨计算结果如表5与表6 所示。
|
|
表 5 装配不同桨自航模拟结果1 Tab.5 Self-propelled simulation results with different propellers 1 |
|
|
表 6 装配不同桨自航模拟结果2 Tab.6 Self-propulsion simulation results with different propellers 2 |
3种盘面比螺旋桨自航计算船尾动压力云图如图5所示,x/L = 0.99处盘面轴向速度分布对比如图6所示。

|
图 5 不同盘面比下船尾表面动压力云图 Fig. 5 The dynamic pressure on the stern surface under different disk surface ratios |

|
图 6 不同盘面比轴向速度分布对比 Fig. 6 Comparison of axial velocity distribution of different disk surface ratios |
分析计算结果可知,随着盘面比增大,自航推力减额变化不大,伴流分数呈减小趋势,船舶的总推进效率呈下降趋势。分析云图可知,不同盘面比螺旋桨下船体压力云图无明显差别,x/L = 0.99处盘面轴向速度分布也基本一致,即船体总阻力变化不大,推力减额也无明显变化。
4 结 语1)以本文方案进行船舶阻力和自航数值仿真,自航船体阻力误差在1%以内,自航因子误差在5%以内,可知结果可信度较高,能满足工程应用需求。
2)不同盘面比下船体阻力变化不显著,推力减额变化不显著,但总推进效率随着桨盘面比增大呈减小趋势,主要原因是随着盘面比增大螺旋桨自身效率降低,同时伴流减小造成船身效率减小。
| [1] |
何惠明. 船艇波浪中自航试验研究[J]. 上海船舶运输科学研究所学报, 2005(1): 3-10. DOI:10.3969/j.issn.1674-5949.2005.01.001 |
| [2] |
CARRICA P M, CASTRO A M, STERN F. Self-propulsion computations using a speed controller and a discretized propeller with dynamic overset grids[J]. Journal of Marine Science and Technology, 2010, 15(4): 316-330. DOI:10.1007/s00773-010-0098-6 |
| [3] |
CASTRO A M, CARRICA P M, STERN F. Full scale self-propulsion computations using discretized propeller for the KRISO container ship KCS[J]. Computers & Fluids, 2011, 51(1): 35-47. |
| [4] |
郭春雨, 赵庆新, 赵大刚. 基于CFD仿真模拟的船模自航试验数据处理[J]. 船海工程, 2013, (3): 17−20.
|
| [5] |
沈兴荣. 船模自航试验数值模拟研究[C]// 第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会, 2012: 1082−1090.
|
| [6] |
胡俊明, 李铁骊, 林焰, 等. 基于RANS法螺旋桨毂帽鳍水动力性能数值研究[J]. 船海工程, 2015(1): 52-55. DOI:10.3963/j.issn.1671-7953.2015.01.013 |
| [7] |
TAHARA Y, WILSON R V, CARRICA P M, et al. RANS simulation of a container ship using a single-phase level-set method with overset grids and the prognosis for extension to a self-propulsion simulator[J]. Journal of Marine Science and Technology, 2006, 11(4): 209-228. DOI:10.1007/s00773-006-0231-8 |
| [8] |
张志荣, 李百齐, 赵峰. 船舶粘性流动计算中湍流模式应用的比较[J]. 水动力学研究与进展(A辑), 2004(5): 637-642. |
| [9] |
RAVEN H C, VAN DER PLOEG A, STARKE A R, et al. Towards a CFD-based prediction of ship performance-progress in predicting full-scale resistance and scale effects[J]. International Journal of Maritime Engineering, 2008, 150: A4. |
| [10] |
黄少锋, 张志荣, 赵峰, 等. 带自由面肥大船粘性绕流场的数值模拟[J]. 船舶力学, 2008(1): 46-53. DOI:10.3969/j.issn.1007-7294.2008.01.007 |
| [11] |
BHUSHAN S, XING T, CARRICA P, et al. Model-and full-scale URANS simulations of Athena resistance, powering, seakeeping, and 5415 maneuvering[J]. Journal of Ship Research, 2009, 53(4): 179-198. DOI:10.5957/jsr.2009.53.4.179 |
 2022, Vol. 44
2022, Vol. 44

