2. 中国人民解放军91697部队,山东 青岛 266000
2. No.91697 Unit of PLA, Qingdao 266000, China
船舶动力定位系统作为深海作业船舶的重要定位装置,通过侧推提供推力对抗环境作用力保持船舶位置不变和航向稳定。
随着计算机运算能力的提高,计算流体力学也得到了快速的发展,多种商用CFD 软件被用于船舶侧推的设计和研究中。Muller[1]使用CFX软件研究了侧推器槽道形状及长度、格栅形状和安装位置对侧推器性能的影响。姚志崇等[2]采用周期性边界条件,对水下机器人横向槽道桨模型的性能进行模拟,得到槽道桨不同方向运动的水动力性能,分析了桨盘面不同位置对侧推性能的影响。严周广[3]和姚震球[4]对四叶可调距 Kaplan 侧推桨进行了 CFD计算,并研究了0航速下螺距比、盘面比、管道长度、管道壁面倾斜度对侧推性能的影响。沈海云[5]使用Fluent软件对侧推器进行了定常水动力性能数值计算,并分析了侧推器在设计工况和过度工况下的流场特性,实现了侧推器水动力性能预报分析。Lu等[6]以一艘典型北海油轮为研究对象,采用STAR-CCM+对由2个主螺旋桨、2个舵和2个首槽道侧推组成的动力定位系统中槽道侧推的水动力性能进行研究。郁程[7]研究了槽道CFD计算中定常与非定常结果的精度,并根据转子叶片负荷计算结果,建立了基于体积力的船身推力模拟方法。
常见槽道侧推是在船身上开一个横向贯穿的圆柱形槽道,通过直角传动轴将动力传输到桨轴带动螺旋桨转动。本文以无轴侧推器为研究对象,可看作将无轴推进器置于槽道内。和普通槽道侧推器相比,无轴侧推没有叶梢与槽道壁之间的间隙,消除了主要噪声源,也不存在桨毂和齿轮箱带来的附加阻力和流动干扰,但国内对这种形式的侧推器研究较少。
本文使用商用CFD软件STAR-CCM+对无轴槽道侧推进行水动力数值模拟,建立一个船舶槽道侧推简化模型,确定了不同边界条件和外域大小对计算结果的影响,并在此基础上研究不同槽道入口对侧推推力的影响。
1 数值计算方法研究 1.1 研究对象无轴推进器将电机转子和推进器桨叶集成,利用电机定转子之间的电磁场作用驱动螺旋桨转动。无轴推进器结构复杂,由桨叶、电机定转子线圈、导管等组成[8]。无轴侧推器将无轴推进器整合到船舶槽道内,用船舶槽道代替无轴推进器导管,将电机定子线圈布置在槽道壁上,电机转子线圈安装在带圆环螺旋桨的外圆上。
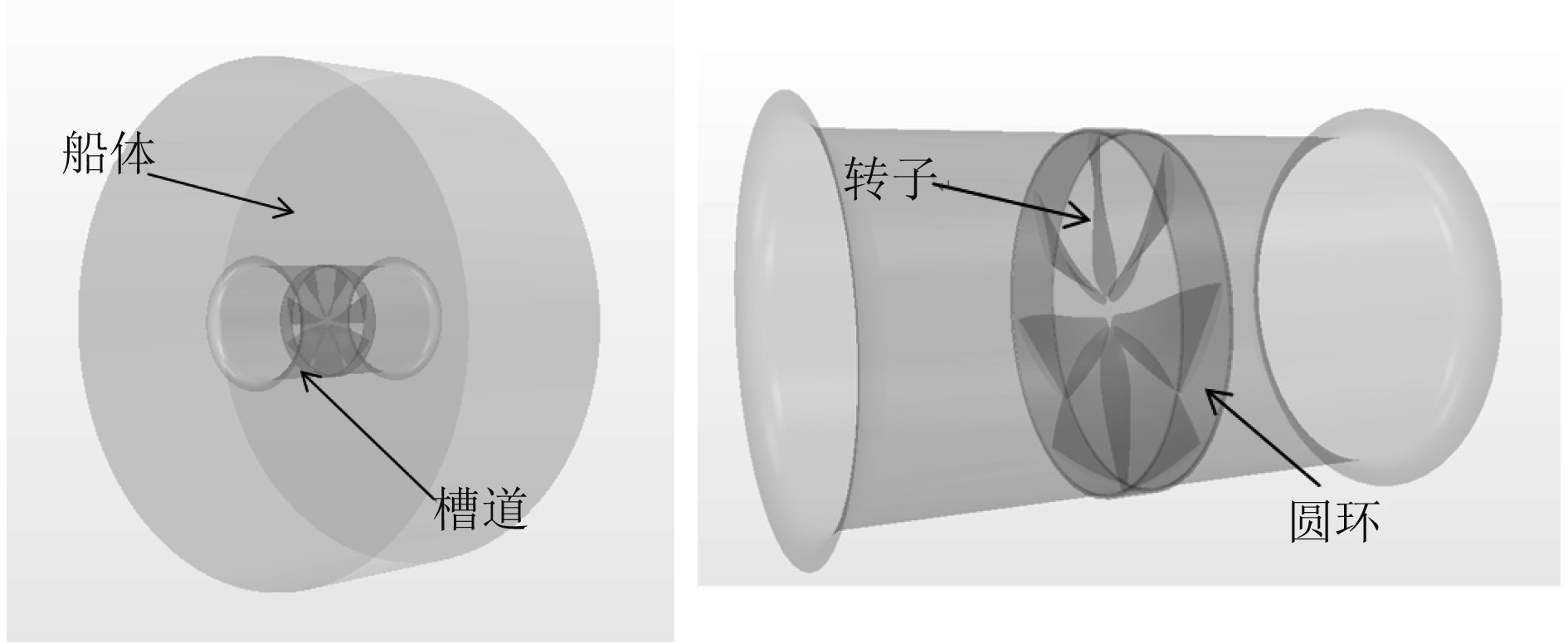
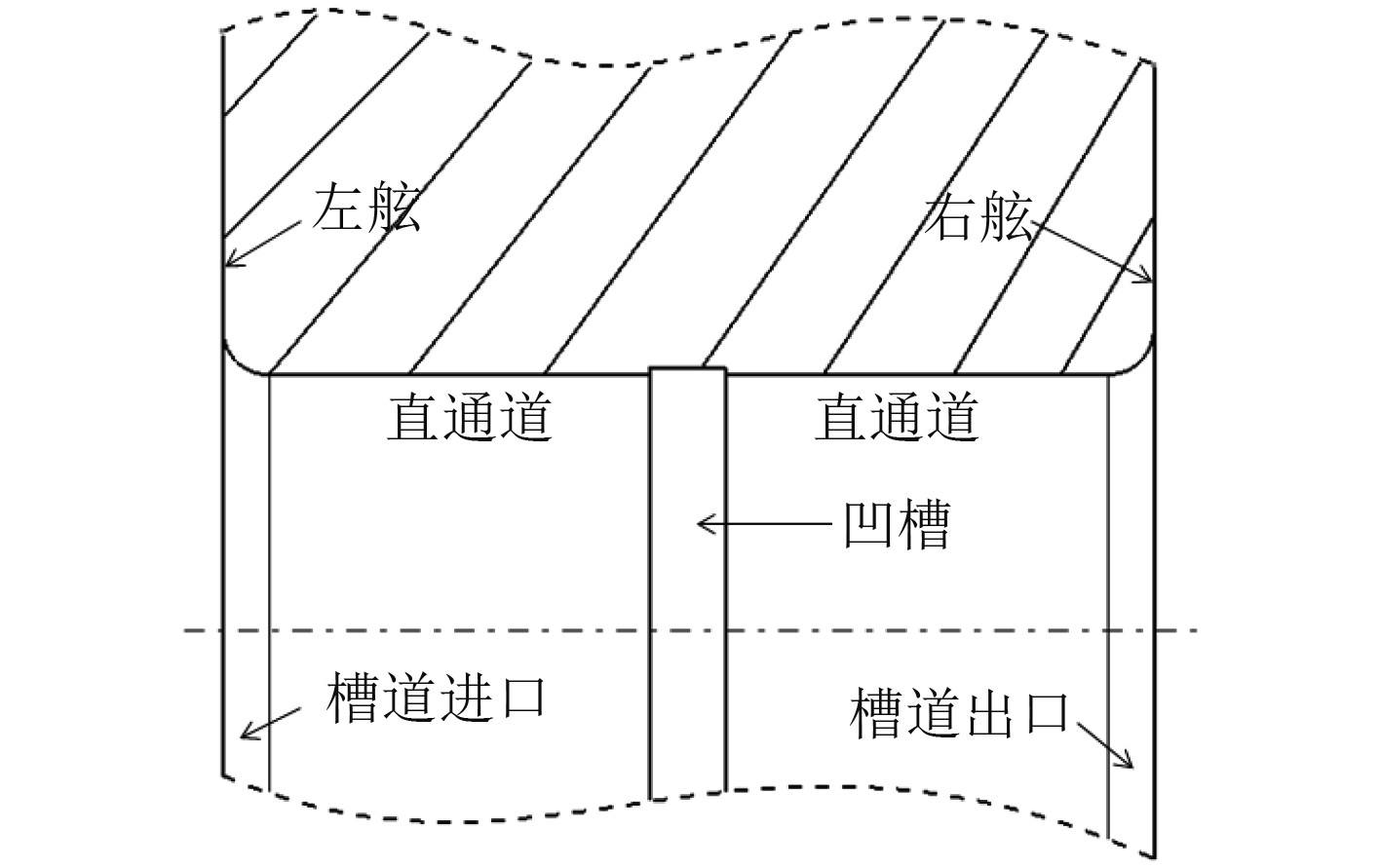
为了便于计算,根据实际槽道侧推器结构进行计算模型简化,以一个圆柱体近似代替船体,在其中心开一个贯穿底面的同心圆柱作为槽道,带圆环的转子置于槽道中央,圆环嵌入槽道凹槽内。槽道长L为2 m,直径D为1.1 m,槽道进口和出口处采用半径0.1 m的圆弧过渡,减小进口处流动分离;转子采用7叶对称桨叶,保证转子正转反转推力相同,转子直径1.1 m,叶梢与圆环固连,转子圆环宽0.15 m,厚0.01 m;圆环与凹槽间隙为6 mm。几何模型如图1所示,图2为船体部分剖视图。
|
图 1 几何模型 Fig. 1 Geometric model |
|
图 2 船体部分剖视图 Fig. 2 A section view of the hull |
参考螺旋桨水动力性能使用推力系数
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}},$ | (1) |
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}},$ | (2) |
| $ {C_F} = \frac{F}{{\rho {n^2}{D^4}}},$ | (3) |
| $ \eta = \frac{{{{[({K_T} + {C_F})/\text{π} ]}^{3/2}}}}{{{K_Q}}}。$ | (4) |
其中:T为带圆环桨叶和凹槽推力之和;Q为带圆环桨叶扭矩;F为船身推力,是螺旋桨抽吸引起的作用在船身上的轴向力,由船体左右舷、槽道进出口、槽道直通管3部分的轴向力组成,方向与T一致(即F为推力)时为正;
在不可压缩流体的条件下,流场的连续性方程和动量方程分别为:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (5) |
| $ \rho \frac{{\partial ({u_i}{u_j})}}{{\partial {x_j}}} = \frac{{\partial p}}{{\partial {x_i}}} + \rho {g_i} + \rho \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right) - \overline {u_i^\prime u_j^\prime } } \right]。$ | (6) |
式中:
方程中出现了新的未知量雷诺应力没有对应的方程求解,所以为使方程封闭就要对雷诺应力项进行某种假定,即建立应力的表达式或者引入新的湍流模型,将其中的脉动值和时均值联系起来。为了实现控制方程组的封闭,本文选择的湍流模型为可实现的
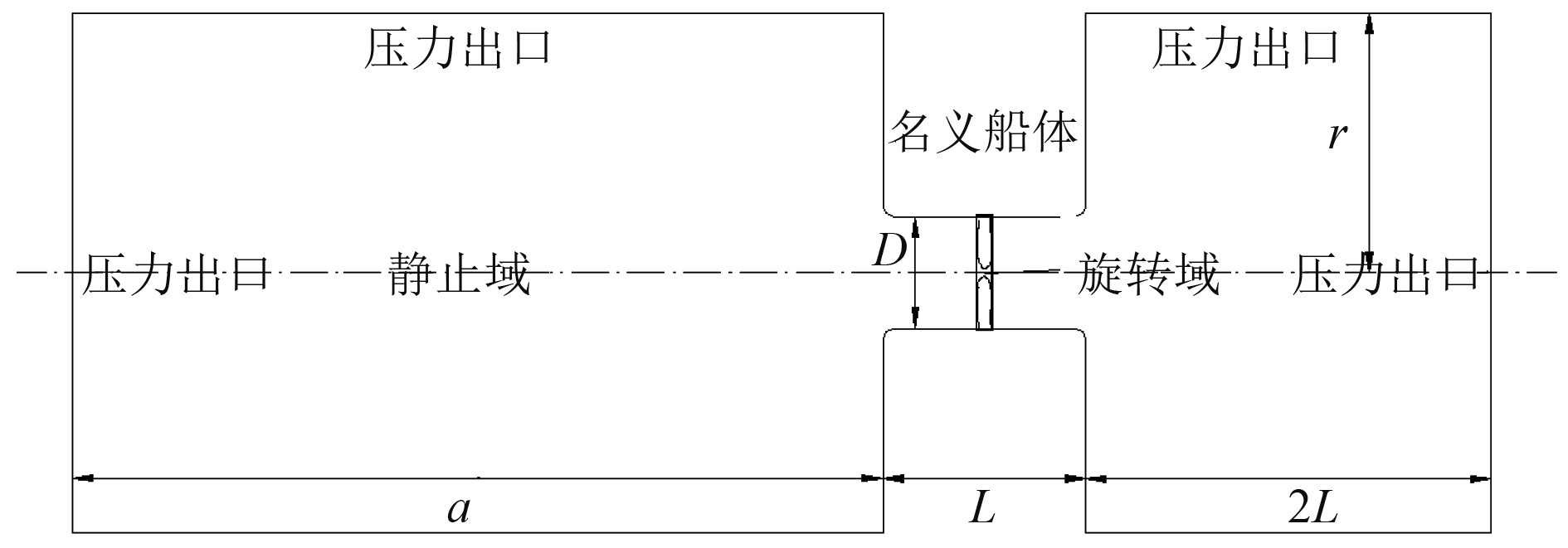
一般认为螺旋桨浸深高于0.625D时可认为螺旋桨不受自由液面的影响,故设置外域为一个长
|
图 3 计算域和边界条件设置 Fig. 3 Calculation domain and boundary condition setting |
网格划分采用非结构网格,由于槽道抽吸作用明显,槽道内流场速度变化剧烈,为捕捉槽道内真实流场,对旋转域、槽道内及槽道进出口附近区域都做了网格加密。采用网格尺度偏小的网格进行计算,减小网格尺度对计算结果的影响。网格如图4所示。

|
图 4 计算域网格划分 Fig. 4 Grid division in computational domain |
对不同外域入口位置和外域半径进行计算,得到不同入口位置和外域半径对槽道侧推水动力的影响。入口位置到槽道入口的距离a选择1L,2L,3L,4L,5L,6L,7L,L为槽道长度。侧面半径r选择为2D,3D,5D,6D,D为转子直径。不同侧面位置对计算结果的影响如表1所示,不同入口位置对计算结果的影响如表2所示。
|
|
表 1 不同计算域大小对推力扭矩的影响 Tab.1 Influence of different computational domain size on thrust torque |
|
|
表 2 不同入口位置对推力扭矩的影响 Tab.2 The influence of different inlet positions on thrust torque |
可以看出不同进口位置、外域半径下
当外域半径大于5D时,
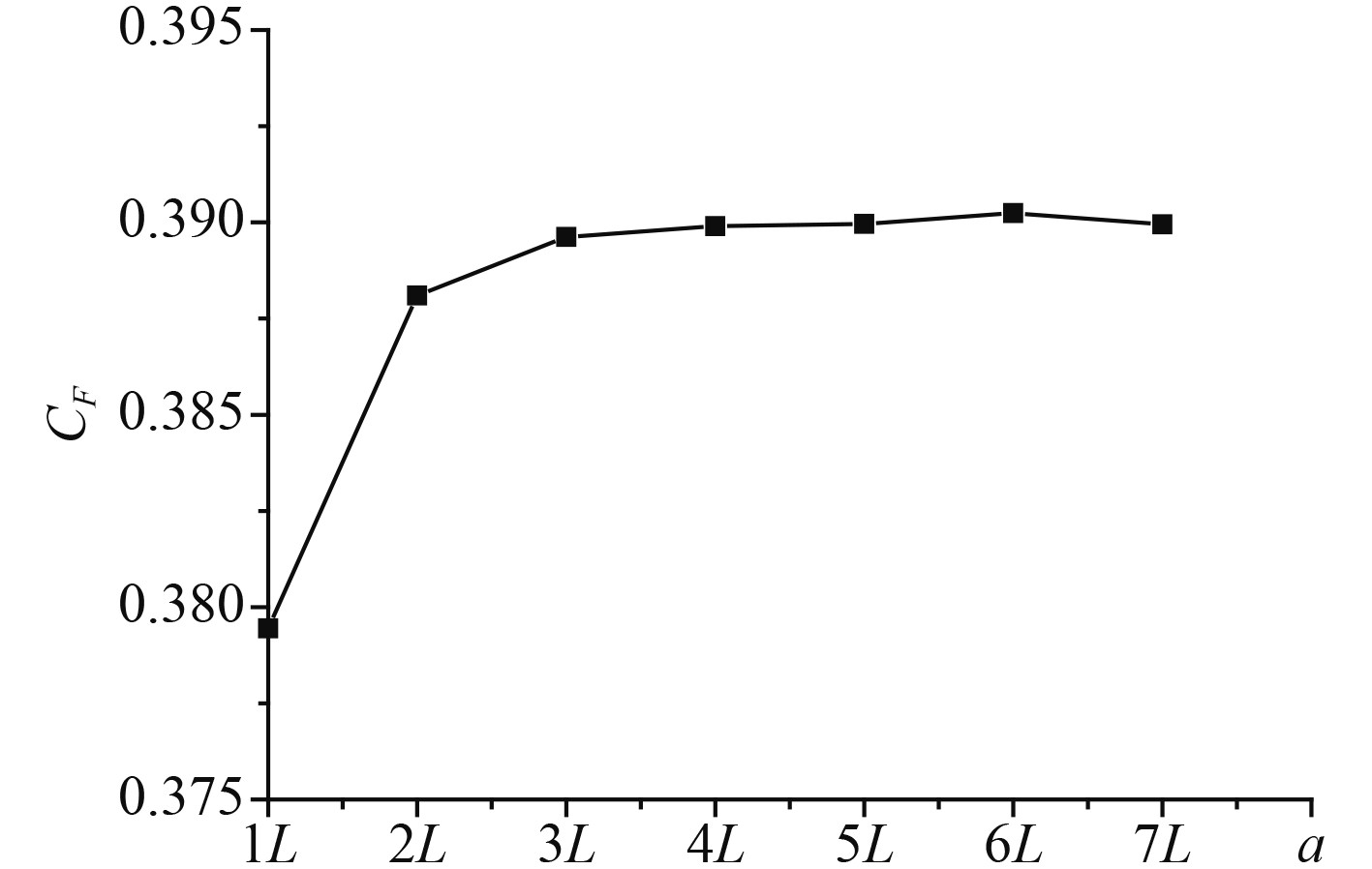
设置外域半径5D,计算得到不同进口位置时
|
图 5 不同进口位置船身推力曲线 Fig. 5 Thrust curves of ship body at different import positions |
由于无轴侧推转子圆环与槽道凹槽之间的间隙较小,间隙中流体速度梯度较大,对网格要求程度高,故在进行网格无关性检验时,保持间隙网格和转子边界层不变,基础尺寸以
|
|
表 3 不同网格模型对槽道侧推水动力性能的影响 Tab.3 Influence of different grid models on hydrodynamic performance of side thrust channel |
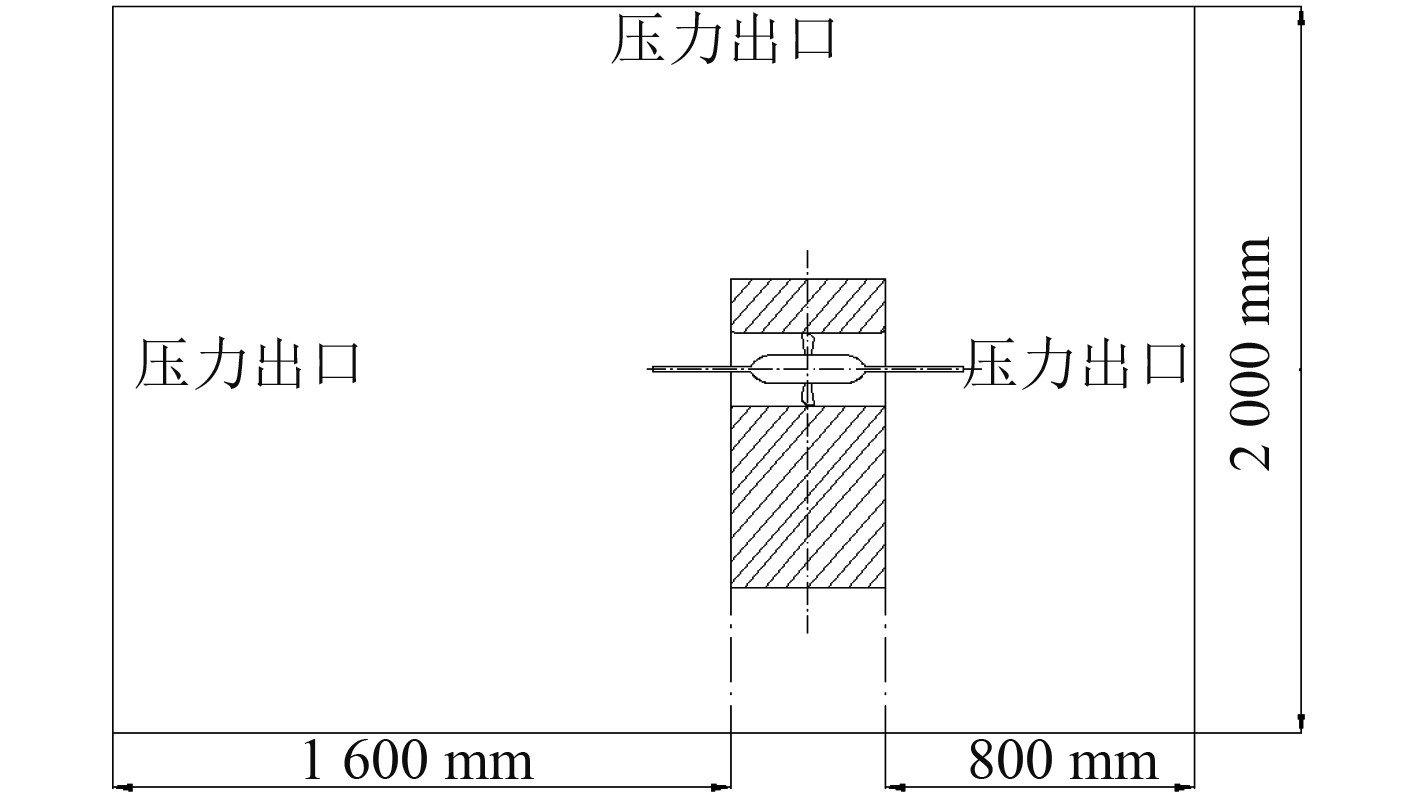
为研究计算方法的可靠性,使用CFD方法对Taniguchi[9]所做侧推器试验进行数值模拟。计算模型按照试验尺寸1∶1建模,模型如图6所示。螺旋桨选择No.1308桨,盘面比0.45,毂径比0.4,直径200 mm。计算域大小和边界条件按照上述CFD方法进行设置,如图7所示。网格尺寸仅以模型比例缩小基础尺寸,保证网格划分与上述方法相同,网格大小如图8所示。

|
图 6 试验模型 Fig. 6 Test model |
|
图 7 边界条件设置 Fig. 7 Boundary condition setting |

|
图 8 计算域网格设置 Fig. 8 Computing domain grid settings |
对试验进行模拟,得到不同螺距比下转子的推力、扭矩,并与试验数据进行比较,如表4所示。可以看出计算结果和试验数据相差不大,当螺距比为1时KT的误差最大值为2.67%。说明CFD方法可以用来计算槽道侧推水动力性能。
|
|
表 4 计算数据与试验数据对比 Tab.4 Comparison of computational and eperimental data |
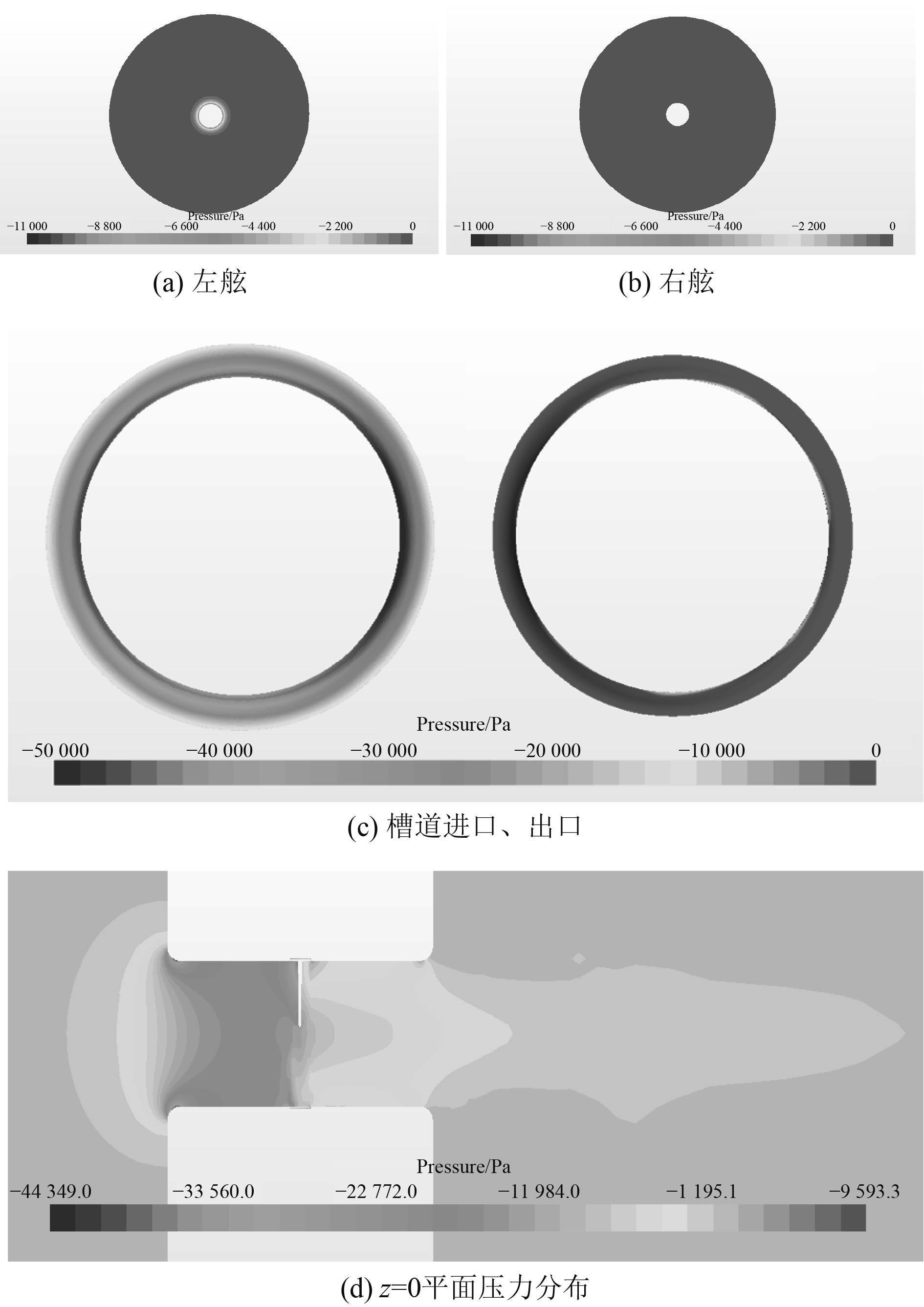
通过对槽道侧推器零航速状态进行数值模拟,发现船身可提供较大推力,为研究其产生原理,将船身分为左舷右舷、槽道入口、槽道出口、直通道和凹槽5部分,如图9所示。对各部分压力进行单独计算,得到各部分压力云图,如图10所示。

|
图 9 船身示意图 Fig. 9 Ship body diagram |
|
图 10 压力分布云图 Fig. 10 Pressure con-tours |
可以看出,船体左舷靠近槽道入口处压力梯度变化明显,右舷压力基本没有变化,槽道进口附近有明显的低压区,但出口处压力近乎为0,所以船身推力主要由于槽道出入口附近压力差而产生轴向推力。这主要因为槽道内螺旋桨抽吸作用,当船体附近流体流过槽道入口时,横截面积突然变小,流速加快,而近壁面速度为0,速度梯度过大,产生流动分离,在槽道进口附近形成低压区,槽道出口处流体高速喷出,对出口处压力影响较小,故在船体槽道出入口附近形成压力差,从而形成与螺旋桨推力同方向的力。
进一步对槽道侧推器各组成部分的推力进行监测,得到各部分产生推力大小,用
|
|
表 5 槽道侧推器推力组成 Tab.5 Thrust composition of channel side thruster |
从表5可知,

|
图 11 船体区域离散化 Fig. 11 Discretization of hull area |
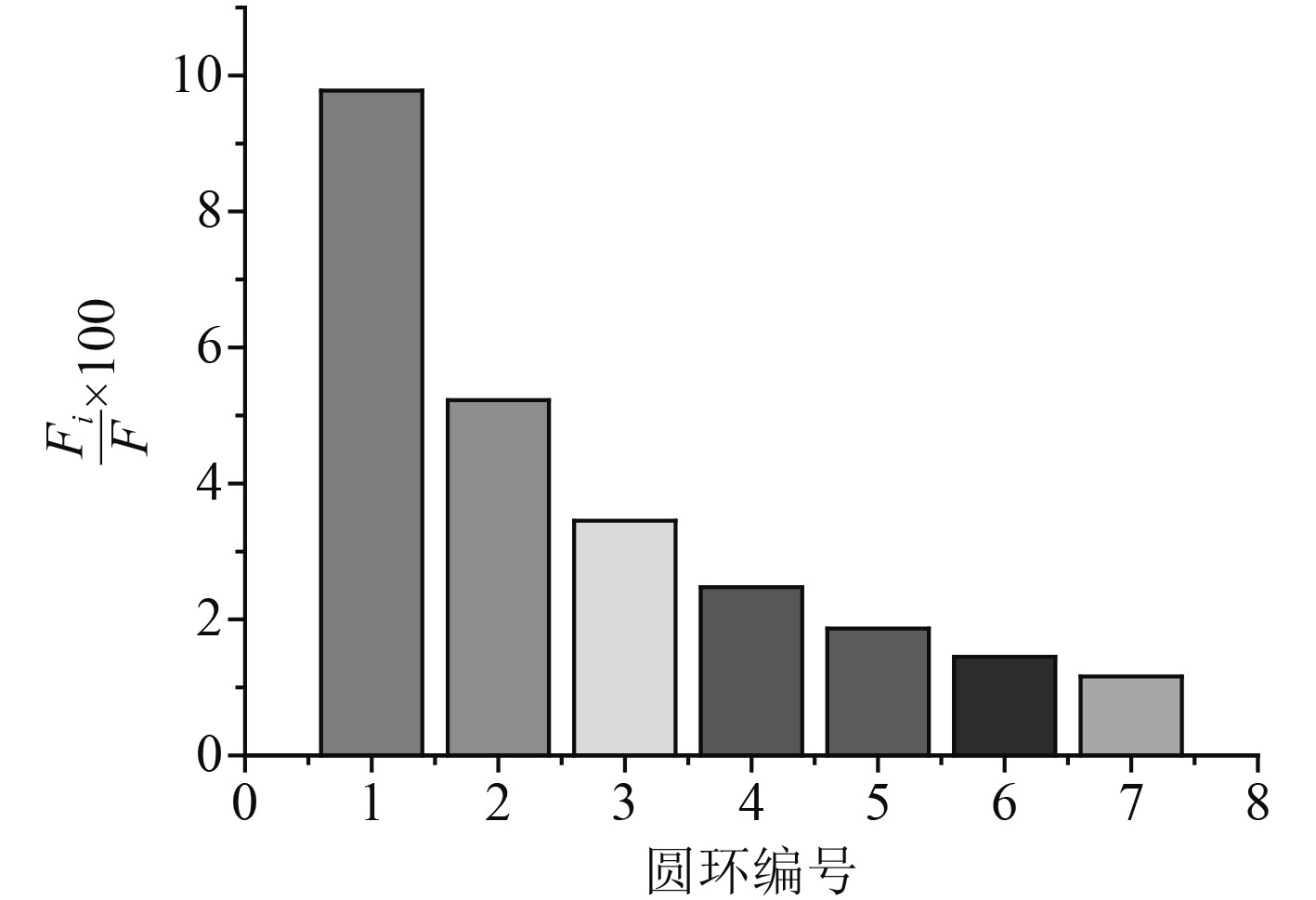
|
图 12 不同圆环推力占比 Fig. 12 The thrust ratio of different rings |
在计算过程中发现,由于槽道侧推器螺旋桨抽吸作用明显,在槽道入口处会出现严重的分离涡,影响槽道内部流场稳定,图13为槽道入口为直角形式时Z=0平面上的速度矢量分布图,图中槽道进口处发生了明显的流动分离,产生的涡向后发展到桨叶附近,故需对槽道入口形状进行优化。采用1/4圆弧作为船体侧舷和槽道壁的过渡,圆弧半径从10 ~100 mm,对不同入口形状建模进行数值计算,不同进口形状Z=0平面上的速度标量分布如图14所示。图15~图17为不同槽道进口形状、转子上游距转子盘面不同距离截面处轴向速度分布图。为进一步分析不同进口形状对槽道侧推水动力性能的影响,通过对水动力进行无因次化得到不同进口形状下水动力曲线如图18所示。

|
图 13 Z=0平面速度矢量图 Fig. 13 Z= 0 plane velocity vector diagram |

|
图 14 不同进口形状Z=0平面速度标量图 Fig. 14 Plane velocity scalar graphs with different inlet shapes Z=0 |

|
图 15 不同进口形状转子盘面前0.1D处沿x轴方向速度分布图 Fig. 15 Velocity distribution along x-axis at 0.1D in front of rotor disks with different inlet shapes |

|
图 16 不同进口形状转子盘面前0.2D处沿x轴方向速度分布图 Fig. 16 Velocity distribution along x-axis at 0.2D in front of rotor disks with different inlet shapes |

|
图 17 不同进口形状转子盘面前0.3D处沿x轴方向速度分布图 Fig. 17 Velocity distribution along x-axis at 0.3D in front of rotor disks with different inlet shapes |
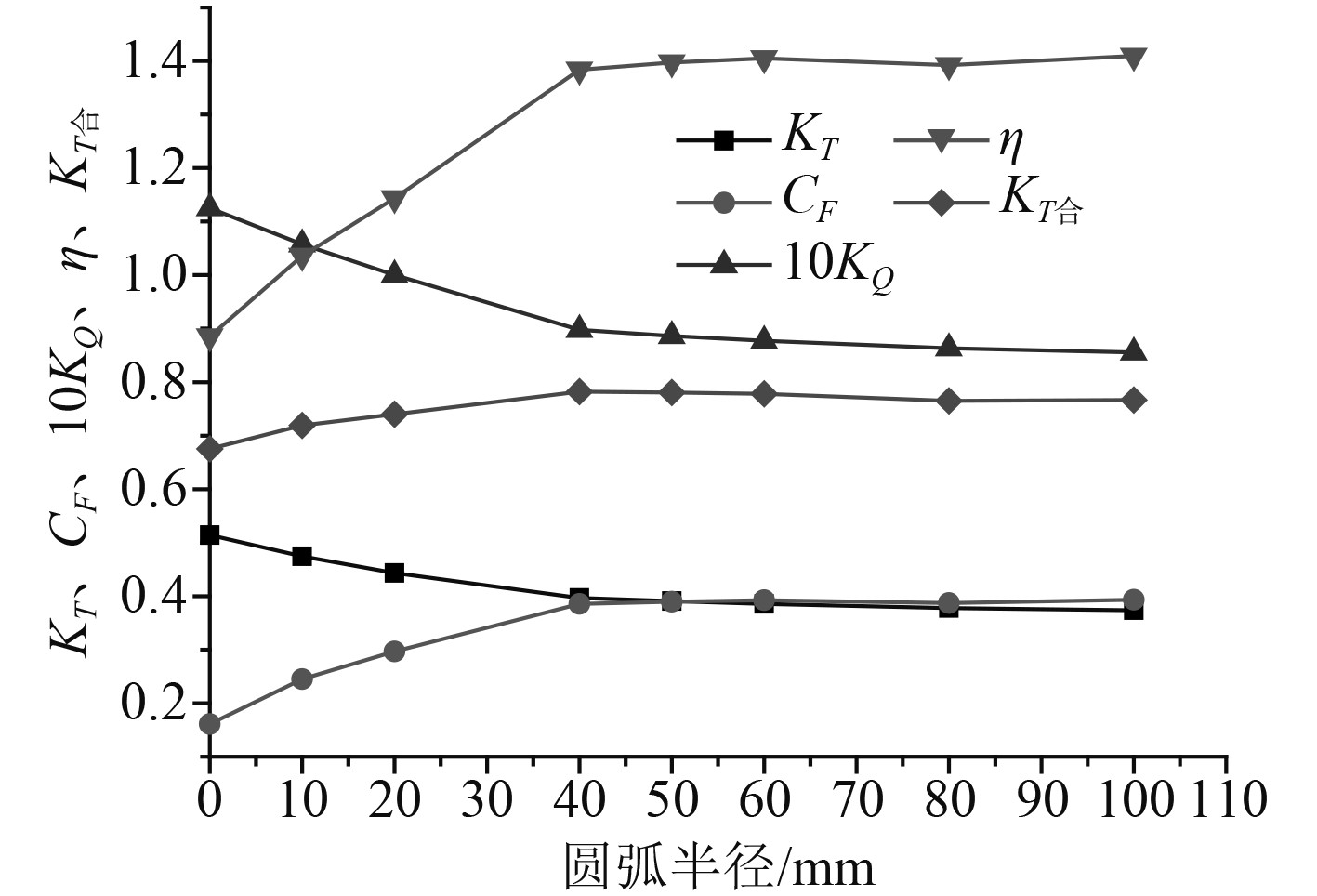
|
图 18 不同槽道进口形式水动力曲线图 Fig. 18 Hydrodynamic curves of different channel inlet forms |
从图14可以看出,随着圆弧半径的增加槽道入口处流动分离减弱,当圆弧半径为50 mm时槽道进口基本不发生流动分离。并且从图15~图17可以看出转子盘面前不同位置处流体轴向速度,当圆弧半径大于50 mm时沿径向分布梯度减小,来流变均匀。
图18中随着槽道进口圆弧半径的增加,螺旋桨推力和扭矩先减小后趋于稳定,船身推力和静态效率参数先增大后趋于平稳。分析其原因转子绕轴旋转,转子叶片越靠近叶梢旋转半径越大,线速度也越大,加之本研究所用转子翼型剖面弦长随着转子半径的增大而增大,导致转子外半径产生推力扭矩占总推力扭矩比例较大。而槽道入口圆弧半径较小时,会在进口处形成流动分离,使靠近槽道内壁一定范围内的流速减小,分离涡下泄在转子盘面前形成回旋流,导致槽道内转子外半径处进速较低,转子外半径产生推力扭矩较大,所以转子推力扭矩较大。
从图18可看出,当圆弧半径达到50 mm时各参数随半径增大变化很小,考虑到槽道的存在破坏了船体表面的完整性,增加了船舶的附体阻力,而过大的圆弧可能会进一步增加船舶附体阻力,因此综合考虑选择槽道侧推进出口圆弧半径为50 mm为宜。
3 结 语本文将无轴推进器与槽道推进结合,对无轴侧推水动力进行数值计算。使用商用软件STAR-CCM+对槽道流场进行模拟,提出一套适合无轴推进器水动力性能研究的数值计算方法,并用该方法对Taniguchi所做侧推器试验进行数值仿真。计算结果和试验数据吻合较好,证明了该方法的可行性。分析了船身推力产生原因主要由于螺旋桨抽吸作用引起槽道进出口附近较大压力差,产生轴向推力。对槽道入口形状进行研究,当圆弧半径达到50 mm时,槽道入口处流动分离基本消除。
| [1] |
MÜLLER S B, ABDEL M M. Numerical investigation of transverse thrusters[J]. Proceedings, STG-Sprechtag–CFD in Ship Design, TUHH, Hamburg. 2007.
|
| [2] |
姚志崇, 曹庆明. 槽道桨水动力性能数值分析[C]//2008年船舶水动力学学术会议暨中国船舶学术界进入ITTC30周年纪念会论文集, 2008.
|
| [3] |
严周广. 基于CFD的船用侧推器水动力性能研究[D]. 镇江: 江苏科技大学, 2012.
|
| [4] |
YAO Z Q, YAN Z G. Hydrodynamic performance analysis and verification of transverse thrusters[J]. Journal of Ship Mechanics, 2012, 16(3): 236-245.
|
| [5] |
沈海云. 可调侧推器设计与水动力性能仿真研究[D]. 杭州: 浙江大学, 2012.
|
| [6] |
LU P, WANG S. CFD simulation of propeller and tunnel thruster performance[C]//ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2014.
|
| [7] |
郁程. 侧推器水动力性能与设计方法研究[D]. 上海: 上海交通大学, 2017.
|
| [8] |
曹庆明, 洪方文, 胡芳琳. 梢部驱动推进器的研究与进展[C]//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集, 2009.
|
| [9] |
TANIGUCHI K, WATANABE K, KASAI H, et al. Investigation into the fundamental characteristics and operating performances of side thruster[R]. Tokyo, Japan: Japan Ship Technology Research Association, 1964.
|
 2022, Vol. 44
2022, Vol. 44

