2. 中国商用飞机有限责任公司北京民用飞机研究中心,北京 102211;
3. 北方车辆集团有限公司车辆研究院,北京 100072
2. Beijing Aircraft Technology Research Institute of COMAC, Beijing 102211, China;
3. China North Vehicle Research Institute, Beijing 100072, China
复合材料具有高强度、高模量、轻量化、良好的可设计性等优点,其中层合板结构被广泛应用于船舶舰体结构设计中,对层合板开展相关优化研究具有重要的工程价值[1]。复合材料的铺层优化设计引起了国内外学者的广泛关注,Tran-Ngoc等[2]借用人工神经网络技术(ANN)对复合材料层合板结构损伤进行预测和优化。白国栋等[3]将深度学习方法运用到复合材料铺层优化设计中。An等[4-5]基于一种二阶近似的离散-连续变量混合算法,实现了复合材料加筋壁板和夹芯板复合材料的多目标优化。而对层合板进行铺层优化设计,需要对复合材料连续变量进行离散,引入铺层角度、铺层厚度、铺层层数等离散设计变量,转化为整数规划问题,变量种类繁多。传统的连续变量优化算法不再适用,需要进行离散组合优化设计。
工程上常用的离散组合优化方法[6]有遗传算法(genetic algorithm, GA)、模拟退火算法(simulated annealing, SA)、差分进化方法(differential evolution, DE),粒子群方法(particle swarm, PS)等。目前对于层合板优化设计相关的研究多为对上述优化算法的改进。孙士平等[7]基于改进的退火算法,以层数和铺层角度为设计变量,对复合材料层合板的最大基础频率和频率带隙问题进行优化。马森等[8]提出一种改进的自适应差分进化算法,并分析了层数对层合板质量最小化优化设计的影响规律。王佩艳等[9]通过改进遗传算法中的变异算子和交叉算子等参数,引入自适应算子,提高了优化效率和稳定性。王轩等[10]考虑层合板间就位效应,应用自适应遗传算法对复合材料结构强度进行预测和优化。Moradi等[11]提出一种混合粒子群-遗传算法(PSO-GA),对层合板所承受最大屈曲载荷进行优化。然而,上述对复合材料连续变量的离散多为区间统计方法,离散效率低,难以对大规模连续变量进行离散求解。因此,本文基于Heaviside函数,提出一种新型阶梯插值模型,建立连续变量与离散物理量的映射关系,从而将离散组合优化问题松弛为连续变量优化问题,最终运用连续变量优化算法求解以实现离散组合优化设计,进一步结合粒子群算法进行求解。
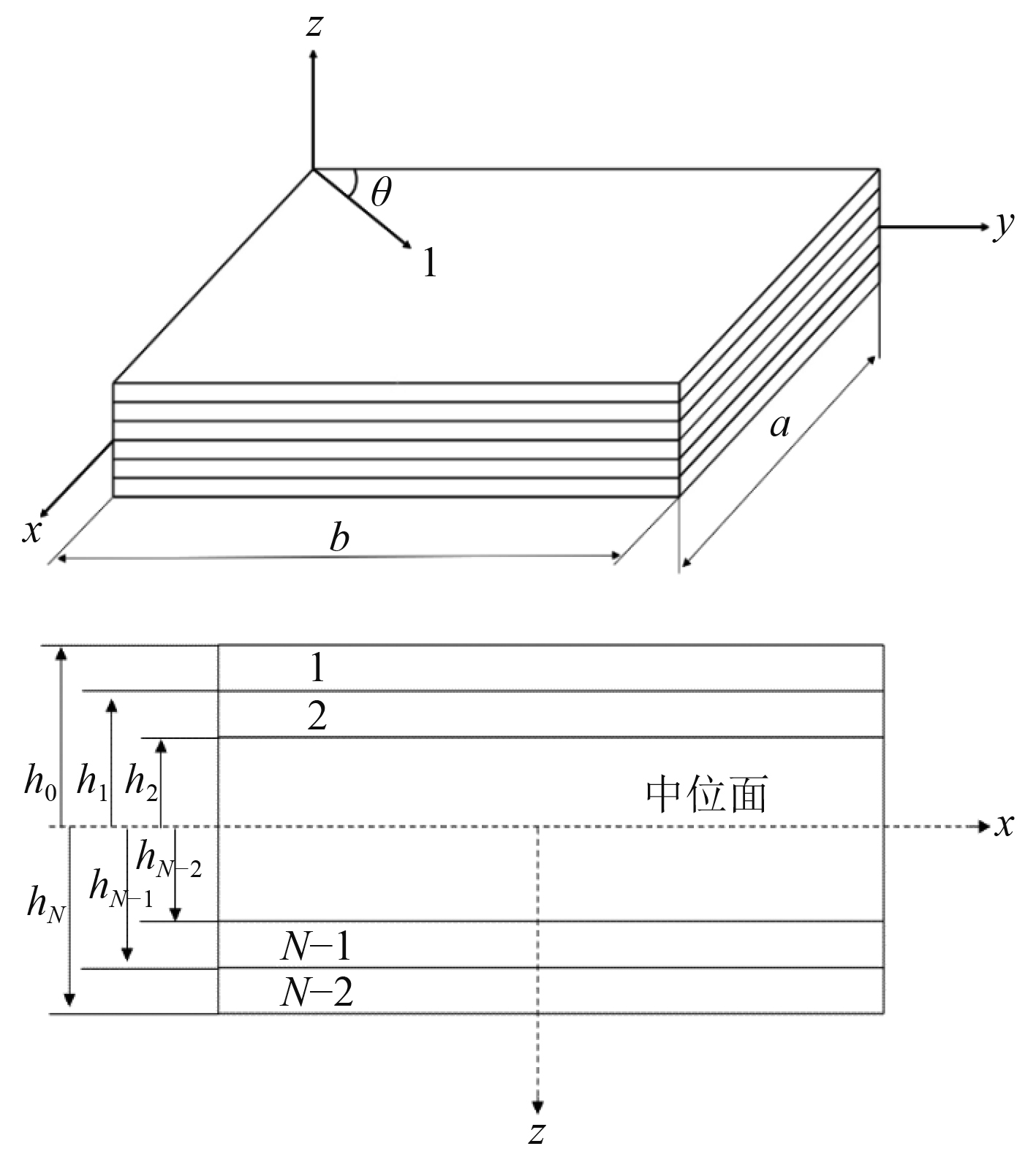
1 层合板基础频率分析以文献[12]中复合材料层合板为例,考虑四边简支约束对称层合板,其几何结构如图1所示。其中,几何参数设定为宽度b为0.25m,总厚度h为0.002 m保持不变,长度a与总层数N为变量用于调整结构长宽比与单层厚度。纤维材料满足均匀化假设(其力学参数见表1),沿Z轴方向堆叠,图中1方向与Y轴正向夹角
|
图 1 复合材料层合板 Fig. 1 The structure of composite laminates |
|
|
表 1 纤维材料属性 Tab.1 Properties of the fiber materials |
通过对经典层合板理论进行推导可得,对称层合板的自由振动控制方程为:
| $ \begin{split}{D_{11}}\frac{{{\partial ^4}w}}{{\partial {x^4}}} +& 4{D_{16}}\frac{{{\partial ^4}w}}{{\partial {x^3}\partial y}} + 2\left( {{D_{12}} + 2{D_{66}}} \right)\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + \\ &4{D_{26}}\frac{{{\partial ^4}w}}{{\partial x\partial {y^3}}} + {D_{22}}\frac{{{\partial ^4}w}}{{\partial {y^4}}} = \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} 。\end{split}$ | (1) |
其中:w为Z方向上的挠度,m;
| $ \omega _1^2 = \frac{{{\text{π} ^4}}}{{\rho h}}\left[ {{D_{11}}{{\left( {\frac{1}{a}} \right)}^4} + 2\left( {{D_{12}} + 2{D_{66}}} \right)\left( {\frac{1}{a}} \right){{\left( {\frac{1}{b}} \right)}^2} + {D_{22}}{{\left( {\frac{1}{b}} \right)}^4}} \right],$ | (2) |
式中,
| $ {D_{ij}} = \sum\limits_{k = 1}^N {\int_{{Z_k}}^{{Z_{k + 1}}} {\overline Q _{ij}^{\left( k \right)}{z^2}{\rm{d}}z\quad i,j = 1,2,6} } 。$ | (3) |
其中:N代表总层数;k代表当前层序;
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_{11}} = \dfrac{{{E_1}}}{{1 - {v_{12}}{v_{21}}}},{Q_{22}} = \dfrac{{{E_2}}}{{1 - {v_{12}}{v_{21}}}}} ,\\ {{Q_{12}} = \dfrac{{{v_{21}}{E_2}}}{{1 - {v_{12}}{v_{21}}}} = \dfrac{{{v_{12}}{E_1}}}{{1 - {v_{12}}{v_{21}}}},{Q_{66}} = {G_{12}}} ,\end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\overline Q }_{11}} = {Q_{11}}{{\cos }^4}\theta + 2\left( {{Q_{12}} + 2{Q_{66}}} \right){{\sin }^2}\theta {{\cos }^2}\theta + {Q_{22}}{{\sin }^4}\theta } ,\\ {{\overline Q }_{12}} = \left( {{Q_{11}} + {Q_{22}} - 4{Q_{66}}} \right){{\sin }^2}\theta {{\cos }^2}\theta + \\ \qquad\quad {Q_{12}}\left( {{{\sin }^4}\theta + {{\cos }^4}\theta } \right) ,\\ {{{\overline Q }_{22}} = {Q_{11}}{{\sin }^4}\theta + 2\left( {{Q_{12}} + 2{Q_{66}}} \right){{\sin }^2}\theta {{\cos }^2}\theta + {Q_{22}}{{\cos }^4}\theta },\\ {{\overline Q }_{16}} = \left( {{Q_{11}} - {Q_{12}} - 2{Q_{66}}} \right)\sin \theta {{\cos }^3}\theta +\\ \qquad \quad\left( {{Q_{12}} - {Q_{22}} + 2{Q_{66}}} \right){{\sin }^3}\theta \cos \theta ,\\ {{\overline Q }_{26}} = \left( {{Q_{11}} - {Q_{12}} - 2{Q_{66}}} \right){{\sin }^3}\theta \cos \theta + \\ \qquad\quad \left( {{Q_{12}} - {Q_{22}} + 2{Q_{66}}} \right)\sin \theta {{\cos }^3}\theta ,\\ {{\overline Q }_{66}} = \left( {{Q_{11}} + {Q_{22}} - 2{Q_{12}} - 2{Q_{66}}} \right){{\sin }^2}\theta {{\cos }^2}\theta + \\ \qquad\quad {Q_{66}}\left( {{{\sin }^4}\theta + {{\cos }^4}\theta } \right)。\end{array}} \right. $ | (5) |
根据式(2)~式(5),即可求解对称层合板基础频率大小
采用插值模型,可以将连续变量优化问题转化为离散组合优化问题进行求解。假设离散组合优化问题可选的离散取值集合为
| $ E(x|\xi ) = {E_0}{\text{ + }}\sum\limits_{i = 1}^N {{{\left\{ {H\left[ {f(x|\xi ) - u(i)} \right]} \right\}}^m}\left( {{E_i} - {E_{i - 1}}} \right)},$ | (6) |
| $ D(x|\xi ) = {D_0}{\text{ + }}\sum\limits_{i = 1}^N {{{\left\{ {H\left[ {f(x|\xi ) - u(i)} \right]} \right\}}^m}\left( {{D_i} - {D_{i - 1}}} \right)}。$ | (7) |
其中:m为拓扑优化罚方法的惩罚因子,一般默认取3;
| $ H(\Delta ) = \left\{ {\begin{array}{*{20}{c}} {1,\vartriangle \geqslant 0} ,\\ {0,\vartriangle < 0} 。\end{array}} \right. $ | (8) |
在实际计算时,Heaviside函数
| $ H\left( \Delta \right) = \frac{1}{{{\text{1 + }}{{\text{e}}^{ - \beta \cdot \Delta }}}}。$ | (9) |
其中
值得说明的是,在材料选择离散组合优化问题中,如果用E0表示孔洞材料,其值理论上为E0=0,但为避免数值奇异问题,工程上用一个小常数表示孔洞材料的物理量。
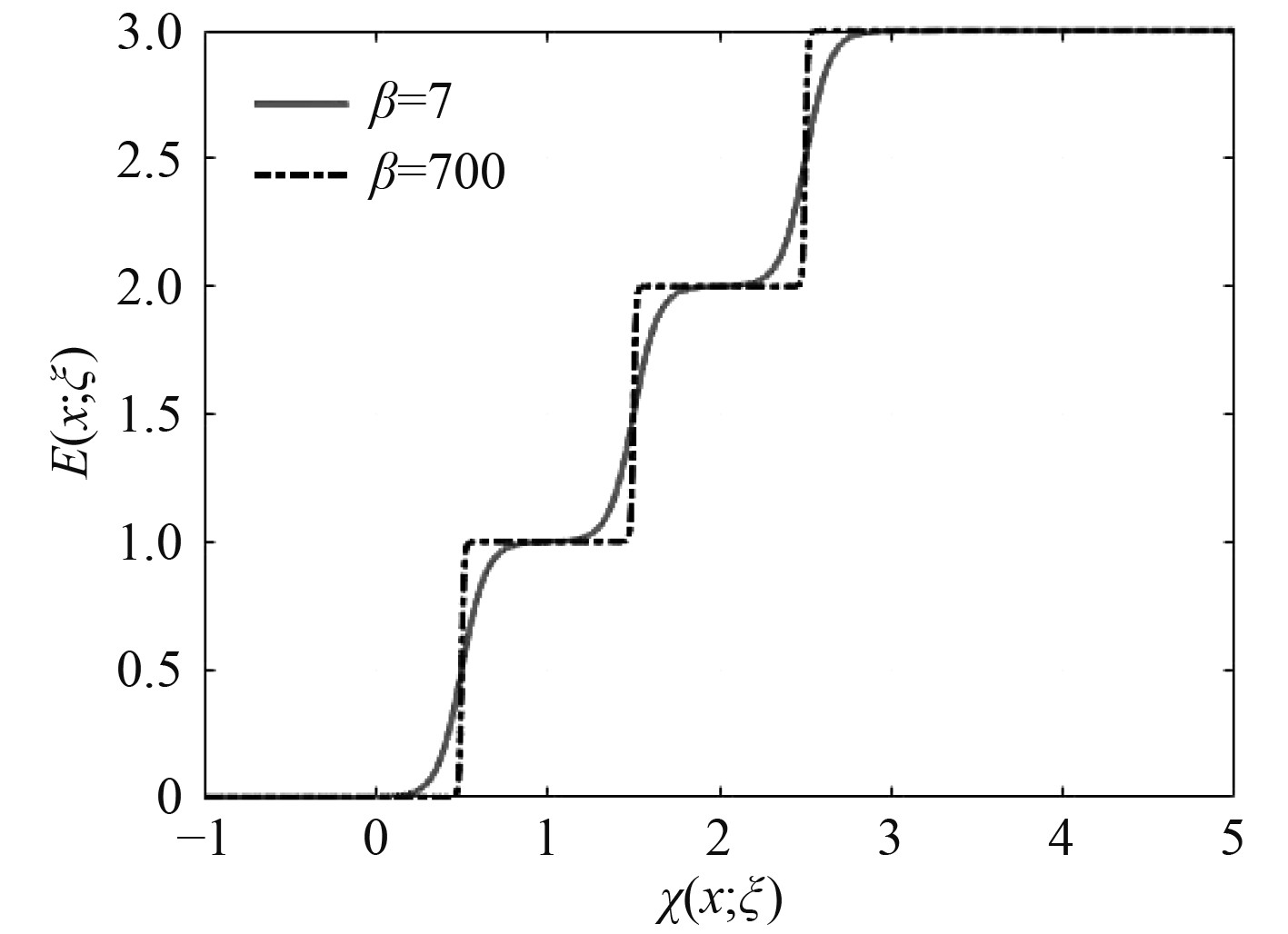
构造的插值模型如图2所示,提出插值模型的目的是将复合函数
|
图 2 阶梯形插值模型函数关系 Fig. 2 The function relationship of stepped interpolation model |
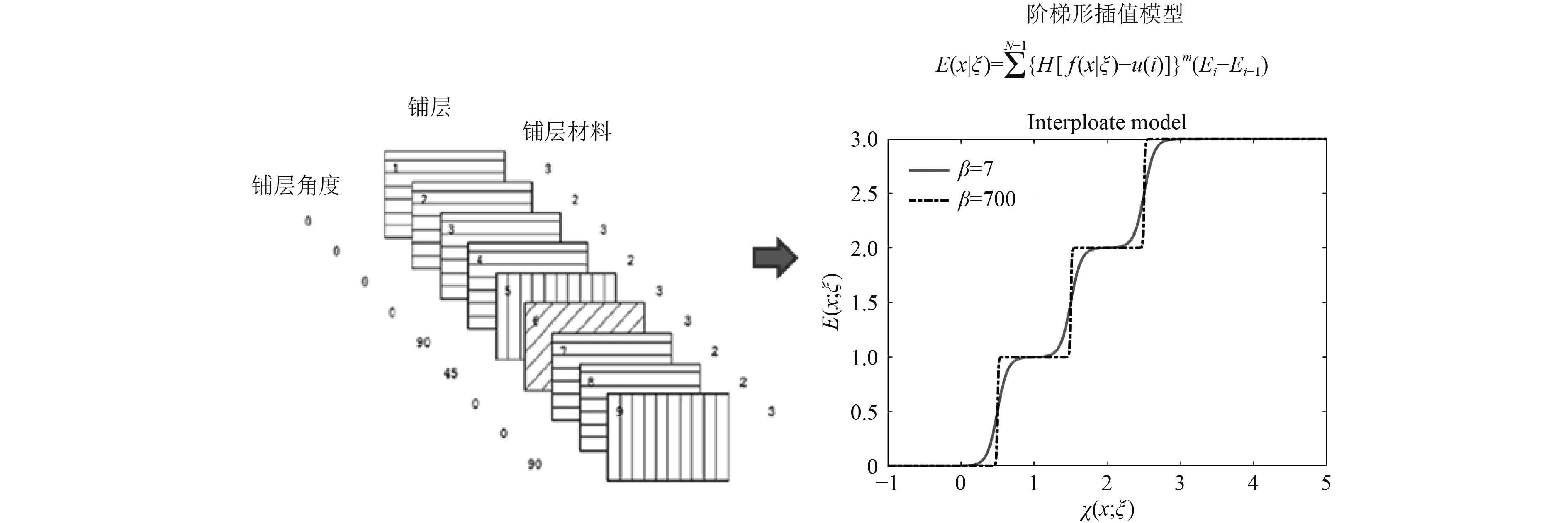
为形象地说明提出的铺层力学设计方法,下面考虑具有100层的复合材料层合板铺层优化问题。假定层合板结构每一铺层可选的材料为N类(如碳纤维、硼纤维等),为简化问题,假设每一个铺层不考虑细观层次的优化设计,即每一个铺层的材料属性(如弹性模量Ei)可采用细观力学方法得到,首先位置向量
|
图 3 复合材料结构阶梯形插值模型铺层力学设计研究方案 Fig. 3 The framwork of mechanical design for lamination of composite structure with stepped interpolation model |
综上所述,提出的铺层设计方案是一种广义普适方案,能够对铺层优化设计过程中的大规模连续变量进行离散,提出的方案将离散组合优化问题转换为连续优化问题,并可利用现有成熟的连续变量优化方法求解,研究复合材料结构的铺层离散组合优化设计问题。
2.2 粒子群优化算法本文选取粒子群优化算法[1](Particle Swarm Optimization,PSO)结合阶梯函数插值模型开展离散组合优化设计工作。粒子群优化算法是基于群体的演化算法, 其思想来源于人工生命和演化计算理论,模拟的是鸟类的觅食行为,将求解问题的空间比作鸟类飞行的时间,每只鸟抽象成没有体积和质量的粒子,来表征一个问题的可行解。粒子运动的快慢和方向分别用粒子速度和粒子位置表示。粒子在每轮迭代过程中会产生最优个体极值,全局最优解是通过搜寻全局范围内的最优个体极值获得的。通过动态改变粒子速度和位置,最终反复迭代得到满足收敛条件的最优解。
每一轮迭代过程中,每个粒子在解空间中的位置和速度通过跟踪2个极值获得更新,更新规则如下:
假设D维空间中共有N个粒子,即每个粒子为一个D维向量,每个粒子表示为:
| $ {X_i} = \left( {{x_{i1}},{x_{i2}}, \cdot \cdot \cdot ,{x_{iD}}} \right),i = 1,2, \cdots N ,$ | (10) |
每个粒子的速度为:
| $ {V_i} = \left( {{v_{i1}},{v_{i2}}, \cdots {v_{iD}}} \right),i = 1,2, \cdots N ,$ | (11) |
第i个粒子目前搜索的最优位置(个体极值)为:
| $ {P_{besti}} = \left( {{p_{i1}},{p_{i2}}, \cdots {p_{iD}}} \right),i = 1,2, \cdots N,$ | (12) |
粒子群目前搜索到的最优位置(全局极值)为:
| $ {g_{best}} = \left( {{g_1},{g_2}, \cdots {g_D}} \right),$ | (13) |
速度的更新公式为:
| $ {V_{i + 1}} = \omega {V_i} + {c_1}{r_1}\left( {{p_{besti}} - {x_i}} \right) + {c_2}{r_2}\left( {{g_{besti}} - {x_i}} \right)。$ | (14) |
其中:r1,r2为[0,1]随机数;
| $ {\omega ^{\left( i \right)}} = \left( {{\omega _{ini}} - {\omega _{end}}} \right)\left( {{G_k} - g} \right)/{G_k} + {\omega _{end}}。$ | (15) |
式中:
首先建立优化问题的目标函数。考虑层合板每个铺层角
| $\begin{split} &\min {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {w_1}(\theta ) \\ & {\text{s.t.}} - {\kern 1pt} \;{90^ \circ } \leqslant {\theta _i} \leqslant {90^ \circ },\;\;i = 1,2, \cdots ,n ,\\ & \theta = {[{\theta _1}\;{\theta _2}\; \cdots {\theta _{i - 1}}\;{\theta _i}\;{\theta _{i + 1}}\; \cdots {\theta _n}]^{\text{T}}}。\end{split} $ | (16) |
针对下述3个问题,以结构基频最大化为目标,分别对不同长宽比的复合材料层合板进行铺层角度离散优化。
1)材料选取玻璃纤维/环氧树脂,总层数n为16,纤维铺层角度在[−90,90]内,以45°为增量进行选择。
2)材料选取亚麻纤维/环氧树脂,总层数n为16,纤维铺层角度在[−90,90]内,以45°为增量进行选择。
3)材料选取碳纤维/环氧树脂,总层n为8,纤维铺层角度在[−90,90]内,以15°为增量进行选择。
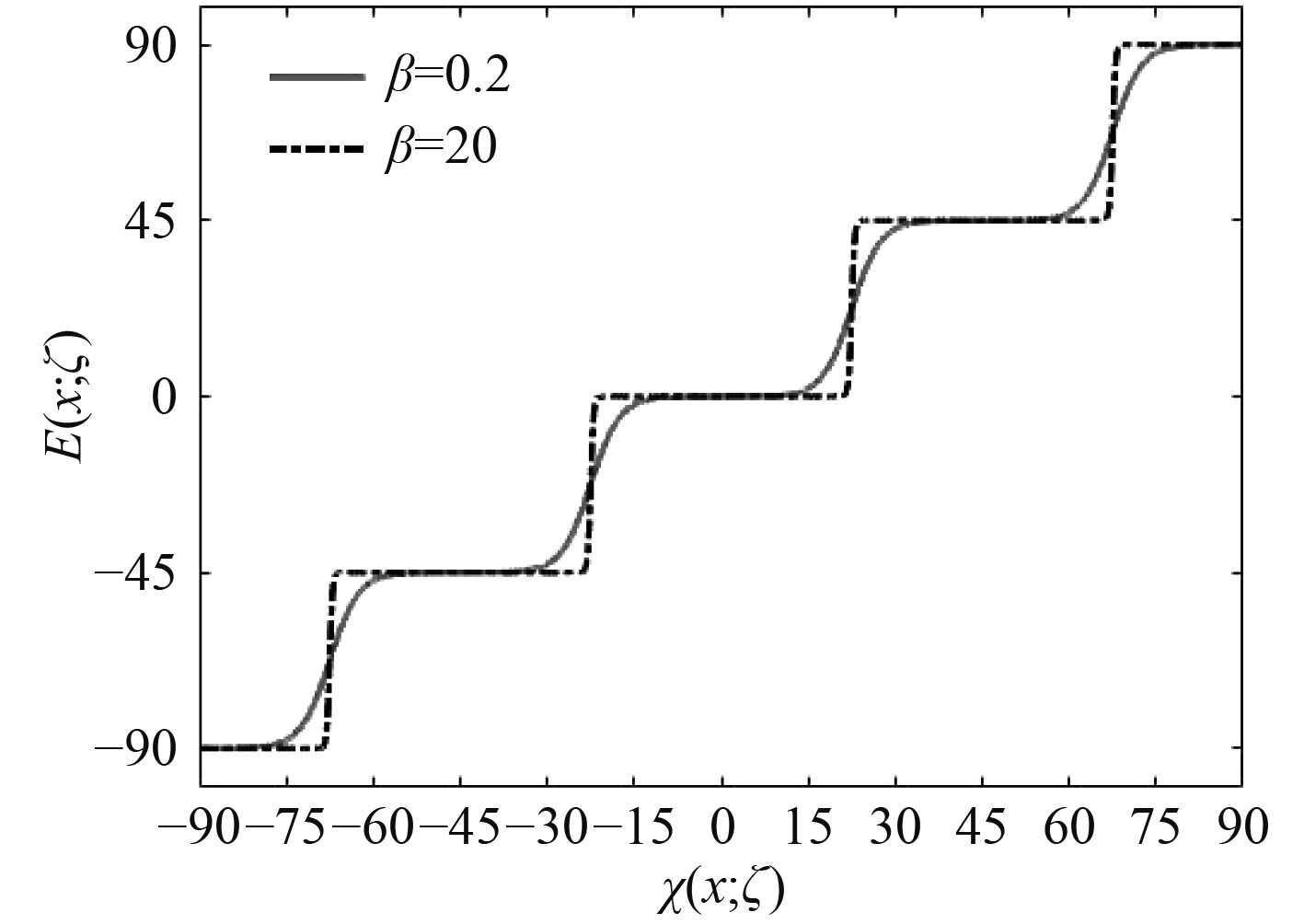
接着根据不同问题的离散特征,建立不同问题的阶梯函数插值模型。由设计变量的特定离散值可知,问题1和问题2的阶梯插值模型函数相同,其中i=4,
|
图 4 问题1和问题2阶梯插值模型 Fig. 4 Interpolation model of problem1 and problem2 |
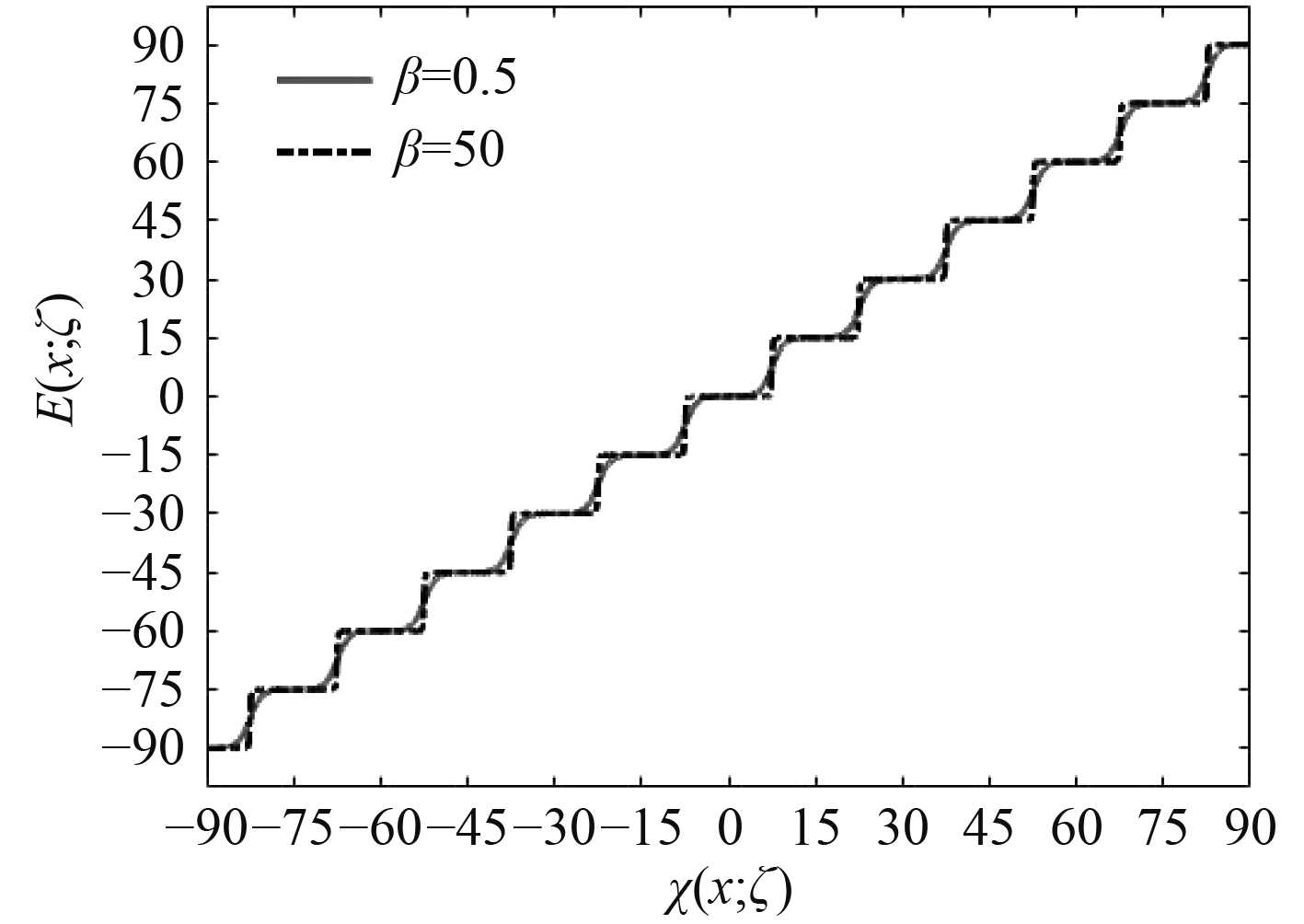
|
图 5 问题3阶梯插值模型 Fig. 5 Interpolation model of problem3 |
应用阶梯函数插值模型,将铺层角度连续变量映射为规定离散值,再结合粒子群优化程序,对式(16)描述的层合板顺序优化问题进行求解。将得到的结果与文献中应用差分进化算法(differential evolution algorithm,DE)、模拟退火算法(simulated annealing algorithm,SA)所得到的结果进行对比,如表2~表4所示。
|
|
表 2 问题1最大基频优化结果 Tab.2 Maximum optimized base frequency of problem 1 |
|
|
表 3 问题2最大基频优化结果 Tab.3 Maximum optimized basic frequency of problem 2 |
|
|
表 4 问题3最大基频优化结果 Tab.4 Maximum optimized basic frequency of problem 3 |
可以看出,3种优化方法在不同长宽比下得到的铺层方案有所差异,但最大基频优化结果完全一致,充分证明了本文所提出的阶梯函数插值模型结合粒子群算法的离散组合优化设计方法在复合材料结构离散优化设计上的有效性。
5 结 语1)提出了阶梯插值模型,可以将复合材料连续变量转化为离散物理量,进一步嵌入到优化算法中求解。
2)以铺层角度为设计变量,基于提出的插值模型和粒子群搜索算法建立了对称复合材料层合板频率特性优化的离散组合设计方法,实现了层合板频率优化问题的铺层设计,与文献[12]结果比较说明,基于阶梯插值模型的粒子群优化算法具有更好的全局搜索能力和计算稳定性,适合求解复合材料层合板的铺层优化问题。
| [1] |
NIKBAKT S, KAMARIAN S, SHAKERI M. A review on optimization of composite structures Part I: Laminated composites[J]. Composite Structures, 2018, 195: 158-185. DOI:10.1016/j.compstruct.2018.03.063 |
| [2] |
TRAN-NGOC H, KHATIR S, HO-KHAC H, et al. Efficient Artificial neural networks based on a hybrid metaheuristic optimization algorithm for damage detection in laminated composite structures[J]. Composite Structures, 2021, 262: 113339. DOI:10.1016/j.compstruct.2020.113339 |
| [3] |
白国栋, 童小燕, 姚磊江. 基于深度学习的复合材料铺层优化方法[J]. 复合材料科学与工程, 2020(7): 68. DOI:10.3969/j.issn.1003-0999.2020.07.010 |
| [4] |
AN H, CHEN S, HUANG H. Multi-objective optimization of a composite stiffened panel for hybrid design of stiffener layout and laminate stacking sequence[J]. Structural and Multidisciplinary Optimization, 2018, 57(4): 1411-1426. DOI:10.1007/s00158-018-1918-2 |
| [5] |
AN H, CHEN S, HUANG H. Multi-objective optimal design of hybrid composite laminates for minimum cost and maximum fundamental frequency and frequency gaps[J]. Composite Structures, 2019, 209: 268-276. DOI:10.1016/j.compstruct.2018.10.075 |
| [6] |
XU Y , ZHU J , WU Z , et al. A review on the design of laminated composite structures: constant and variable stiffness design and topology optimization[J]. Advanced Composites & Hybrid Materials, 2018.
|
| [7] |
孙士平, 张卫红. 基于改进模拟退火算法的复合材料层合板频率优化[J]. 复合材料学报, 2015, 32(3): 902-910. |
| [8] |
马森, 赵启林. 基于差分进化算法的复合材料层合板优化设计[J]. 复合材料科学与工程, 2018(10): 70. DOI:10.3969/j.issn.1003-0999.2018.10.011 |
| [9] |
王佩艳, 赵晨, 耿小亮, 等. 基于改进自适应遗传算法的层合板铺层顺序优化方法[J]. 科学技术与工程, 2018, 6. DOI:10.3969/j.issn.1671-1815.2018.15.002 |
| [10] |
王轩, 许诺, 周春苹, 等. 考虑就位效应的复合材料层合板自适应遗传算法铺层优化[J]. 复合材料科学与工程, 2020, 323(12): 17-22. |
| [11] |
MORADI S, VOSOUGHI A R, ANJABIN N. Maximum buckling load of stiffened laminated composite panel by an improved hybrid PSO-GA optimization technique[J]. Thin-Walled Structures, 2021, 160: 107382. DOI:10.1016/j.tws.2020.107382 |
| [12] |
MELIH S, LEVENT A. Stochastic optimization of graphite-flax/epoxy hybrid laminated composite for maximum fundamental frequency and minimum cost[J]. Engineering Structures, 2018, 174: 675-687. DOI:10.1016/j.engstruct.2018.07.043 |
 2022, Vol. 44
2022, Vol. 44

