2. 中国人民解放军92196部队,山东 青岛 266000
2. No.92196 Unit of PLA, Qingdao 266000, China
潜艇航行期间,处于复杂的水下环境,一旦受到碰撞、搁浅等偶然性载荷作用,或者舷间液舱出现超压破坏,都可能引起耐压艇体外肋骨的侧倾。肋骨的侧倾损伤将直接影响耐压艇体的承载能力,即潜艇的下潜深度。潜艇肋骨侧倾损伤后,为恢复其技术状态,应及时进坞修理。但由于作战需求,或者其他原因无法及时修理,必须带着结构的局部损伤执行任务,此时就需要对损伤后潜艇的剩余强度进行计算与评估,指导潜艇在一定时间内降低性能使用。
近年来,针对水面船舶典型结构的破损剩余强度,国内外学者做过一些理论和试验研究工作。Surko[1]曾对遭受内部爆炸后舰体结构剩余强度进行分析,讨论了板构件剩余强度的计算问题。Paik[2]等基于完整船体极限强度的解析方法,加以改进后提出破损剩余的解析方法。Niessen[3]从保证舰船生命力的角度探讨了受损舰体结构的强度计算问题,提出改进舰体结构设计的一些具体建议。Notaro[4]等釆用Abaqus软件对碰撞和搁浅引起的船体破损剩余强度进行计算,讨论了模型范围、初始缺陷及破损形式的影响。高本国[5]探讨评估破损船体剩余强度的技术背景,研究剩余强度的评估准则和方法,重点讨论碰撞和搁浅2种事故下破损的位置和范围,并釆用非线性有限元方法对一艘集装箱船进行了破损剩余强度算例分析。李晨鹏[6]利用有限元方法,以舱段结构为研究对象,提出了在弯曲、扭转荷载分别作用下,考虑厚度影响、含裂纹损伤下的舱段结构剩余极限强度评估公式,为具有缺陷舰船舱段结构剩余极限强度评估提供依据。目前对潜艇典型结构受损后的剩余强度研究仍然较少,白雪飞[7]提出了受损伤环肋圆柱壳的“剩余强度”概念,并以“涡形凹陷”作为损伤变形的典型形状,考察了环肋圆柱壳在静水外压作用下的应力分布和失稳临界压力,并与相应完好状态的环肋圆柱壳进行比较。梅志远[8]以单/双壳体潜艇典型结构为研究对象,分别设计初始深水静压强度相当的典型单/双耐压环肋圆柱壳体结构模型,通过有限元数值方法,对撞击后典型单/双结构耐压壳体结构的剩余强度特性进行比较分析。马晓龙等[9]以受点蚀损伤的环肋圆柱壳为研究对象,用Ansys有限元软件对点蚀深度、直径、分布位置及密度等参数变化对极限强度的影响进行仿真计算,得到一般规律。吕岩松[10]以局部损伤潜艇耐压壳体为研究对象,对局部损伤后的强度进行数值计算,并提出加强方案。上述关于潜艇损伤剩余强度的研究,都是以耐压壳体的变形、腐蚀损伤为研究对象。袁伯伟[11]对潜艇肋骨损伤后,肋骨根部壳板内表面纵向应力进行了理论分析。潜艇肋骨侧倾损伤后,为确定剩余极限下潜深度,需要对耐压艇体的应力、稳定性和极限强度进行全面计算和综合分析。
本文以环肋圆柱壳舱段结构为研究对象,以肋骨侧倾为损伤形式,对其在静水外压作用下的应力分布、稳定性和极限承载能力进行计算,分析肋骨侧倾损伤对耐压艇体力学特性的影响规律,从而为确定损伤后潜艇的极限下潜深度提供技术支撑。
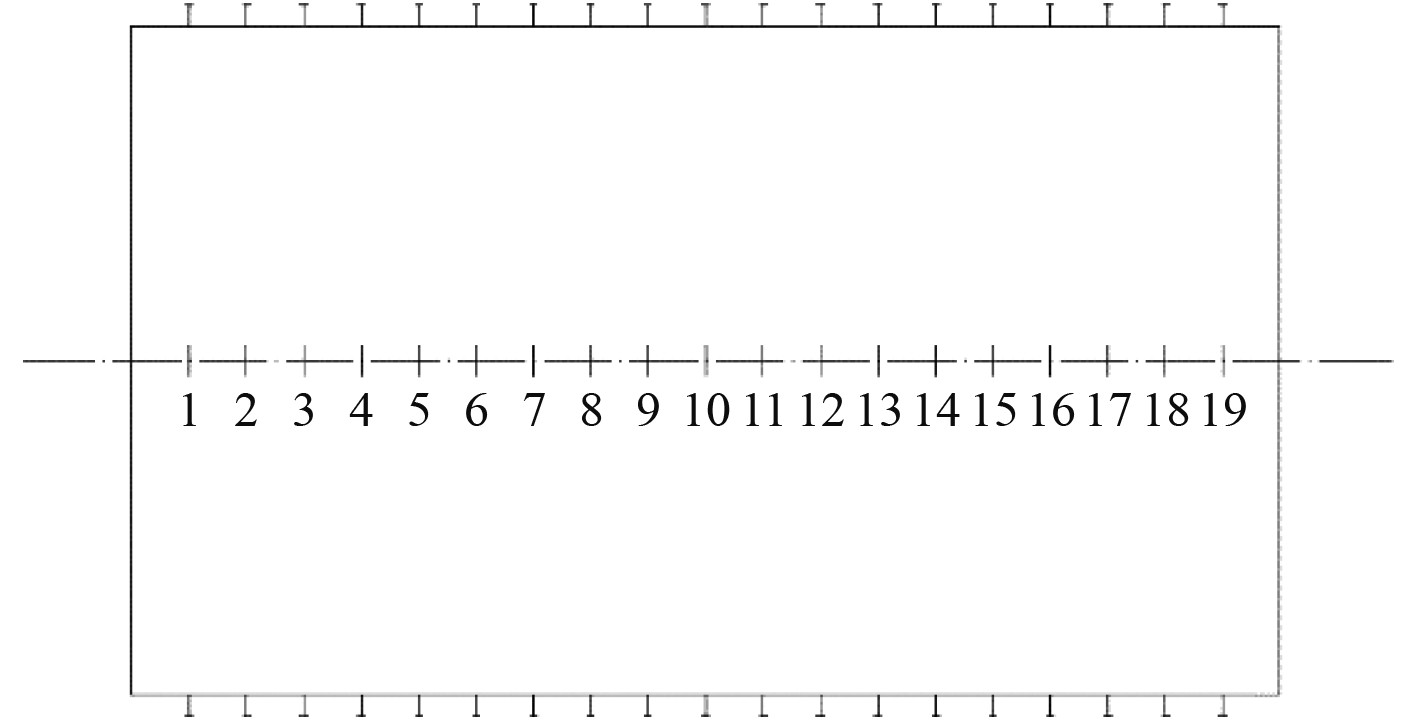
1 肋骨侧倾损伤的环肋圆柱壳计算模型 1.1 计算模型的建立以典型潜艇耐压艇体环肋圆柱壳舱段结构为研究对象,如图1所示。耐压圆柱壳直径D为7 000 mm,长度L为12 000 mm,肋骨间距l为600 mm,壳板厚度为28 mm,T型肋骨尺寸为:⊥
|
图 1 环肋圆柱壳舱段结构图 Fig. 1 Ring-stiffened cylindrical shell |
为分析不同损伤形式下环肋圆柱壳的力学特性,分别改变肋骨侧倾角度、侧倾的肋骨数目,建立系列有限元模型,分析计算模型的强度、稳定性和极限承载能力。图2为3根肋骨侧倾损伤、变形角度为30°的示意图。
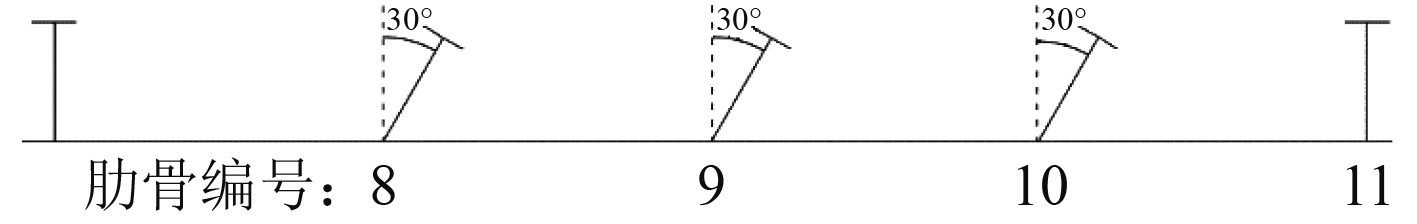
|
图 2 3根肋骨向右侧倾30° Fig. 2 Three ribs deformed 30 degrees to the right |
采用Ansys有限元软件建立有限元模型,壳体、肋骨均采用shell181单元,单元尺度为50 mm,材料弹性模量E=2.1×105 MPa,泊松比µ=0.3,屈服极限σs=590 MPa,有限元模型如图3和图4所示。

|
图 3 损伤前有限元模型 Fig. 3 Finite element model before damage |

|
图 4 损伤后有限元模型(8,9,10,11号肋骨损伤) Fig. 4 Finite element model after damage (No.8,No.9,No.10,No.11 rib were damaged) |
环肋圆柱壳计算模型受静水压力P=4.41 MPa,模型左侧边界为固支,右侧边界仅放松轴向约束,同时以
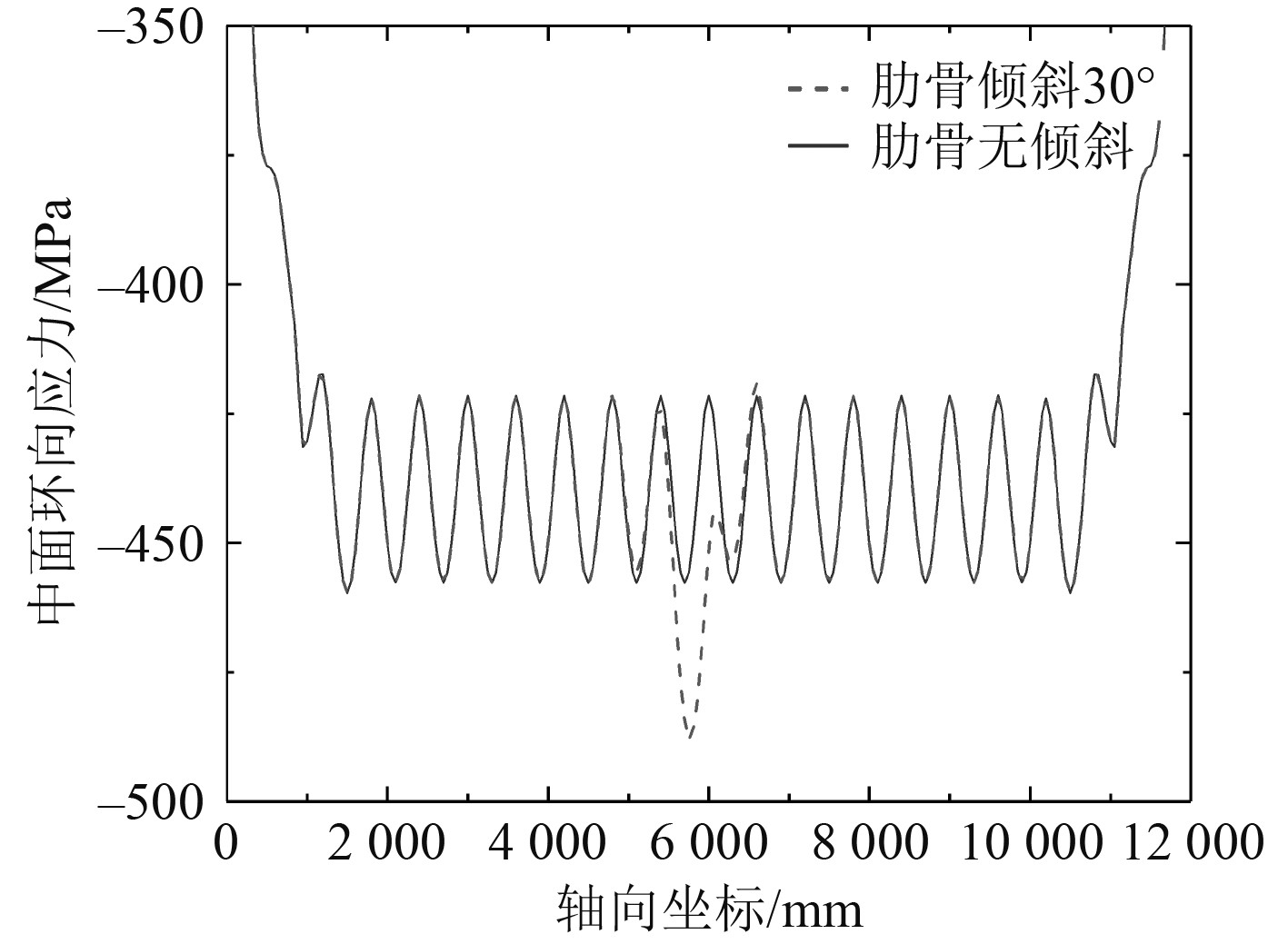
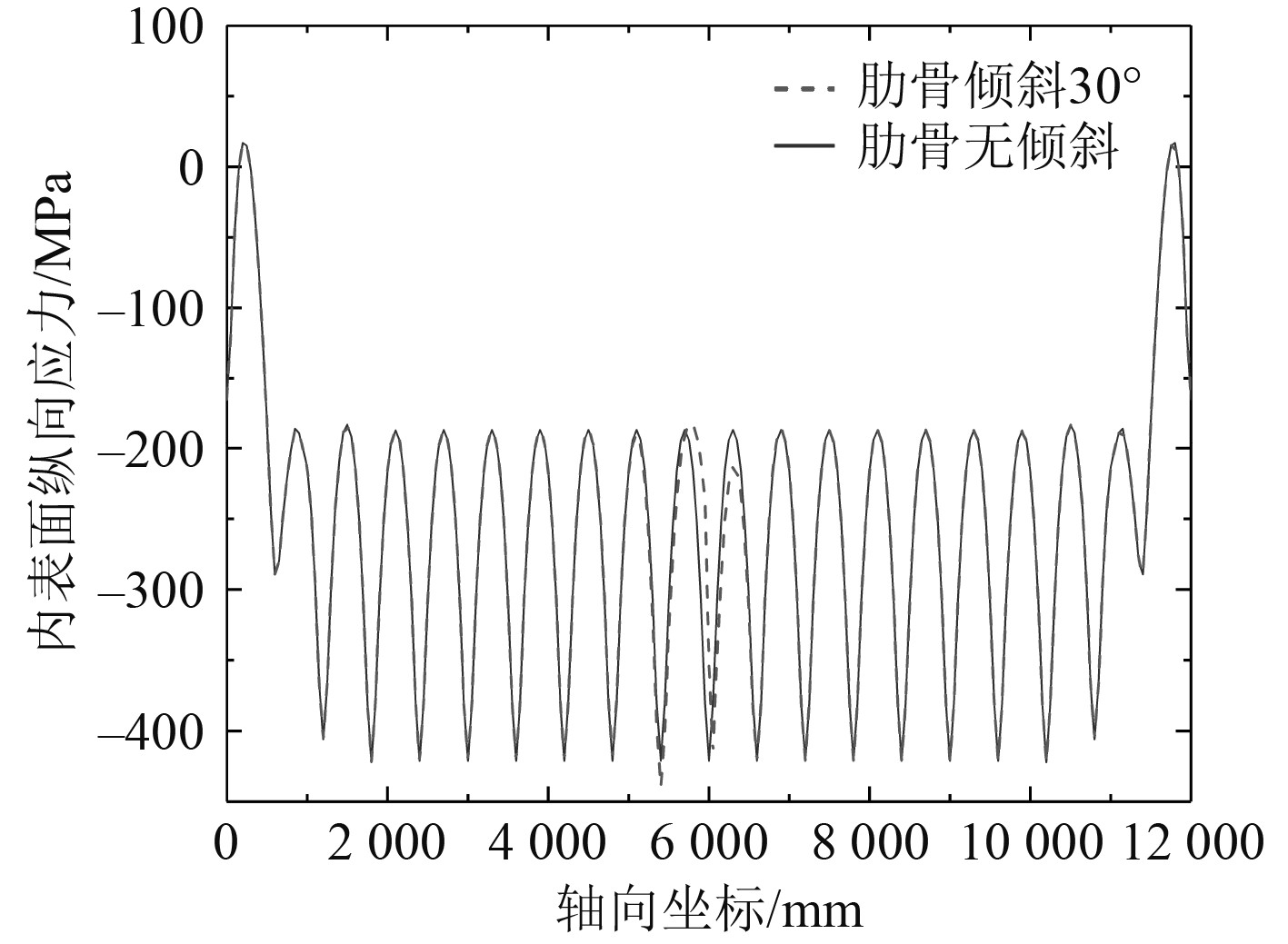
假设计算模型10号肋骨发生向右30°侧倾损伤,图5和图6列出了计算模型壳板内表面纵向应力和中面环向应力分布曲线。可知,10号肋骨向右侧倾后,在10号肋骨和9号肋骨之间的壳板跨中,中面环向应力有较明显提高,损伤肋骨根部壳板的内表面纵向应力较损伤前略有降低。
|
图 5 中面环向应力分布曲线 Fig. 5 Distribution curve of circumferential stress of middle surface |
|
图 6 内表面纵向应力分布曲线 Fig. 6 Distribution curve of internal longitudinal stress |
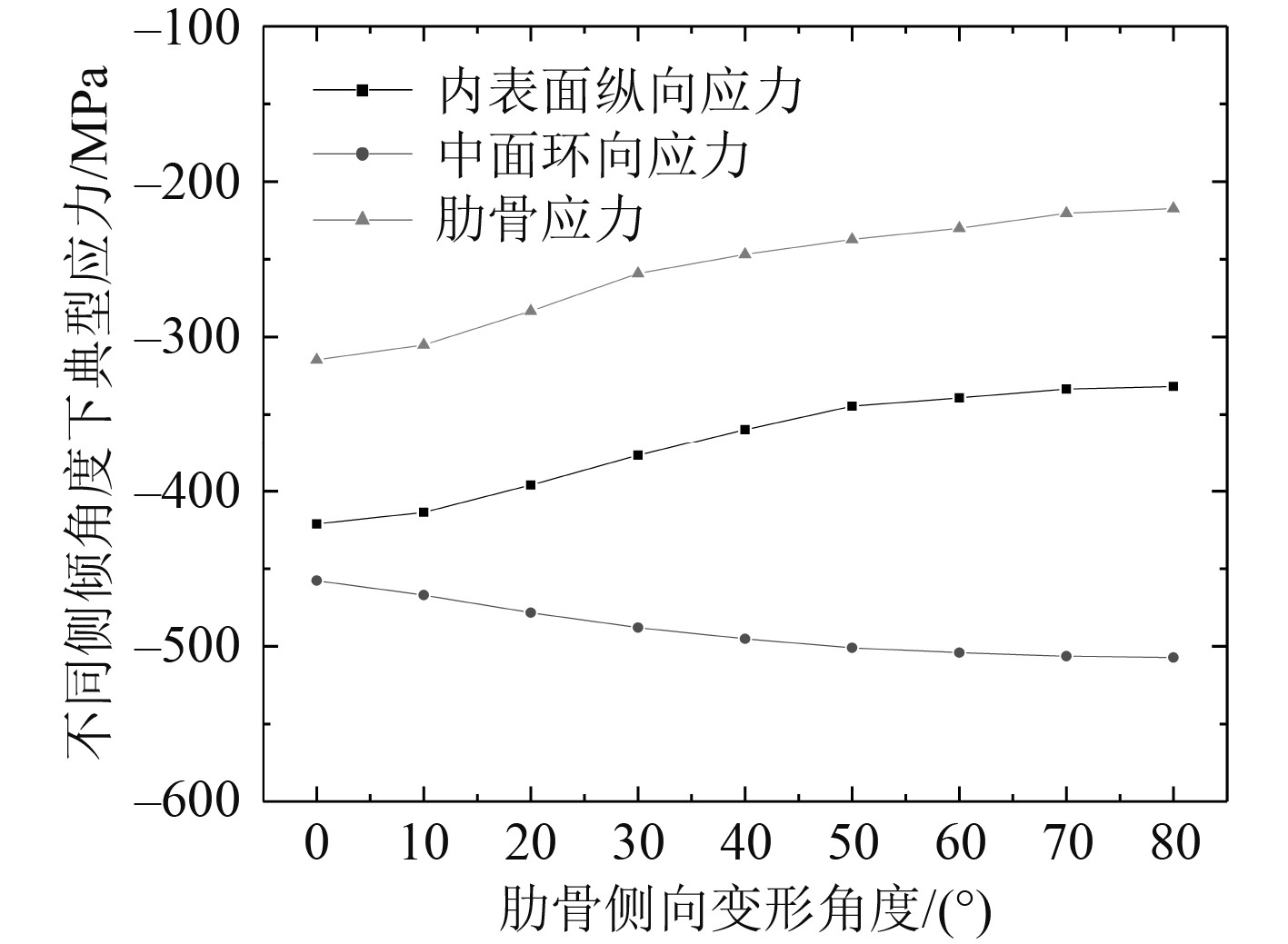
改变10号肋骨向右侧倾角度,分析耐压壳体应力分布规律。表1列出了不同变形角度时,10号肋骨根部内表面纵向应力、10号和9号肋骨跨中壳板中面环向应力和10号肋骨应力计算结果,应力变化曲线见图7。
|
|
表 1 不同肋骨侧倾角度下典型应力计算结果 Tab.1 Calculation results of stress at different inclination angle of rib |
|
图 7 不同倾斜角度时应力变化曲线 Fig. 7 Stress at different inclination angle of rib |
由表1和图7可知,随着侧倾角度的增加,10号肋骨根部壳板内表面纵向应力逐渐降低,10号~9号肋骨跨中壳板中面环向应力逐渐提高,肋骨应力逐渐降低。分析其原因,肋骨侧倾损伤变形后,其径向刚度降低,在静水压力作用下,肋骨对耐压圆柱壳的支撑作用降低,从而造成损伤肋骨附近壳板跨中中面环向应力提高。同时由于损伤肋骨的径向刚度降低,肋骨根部壳板内表面纵向应力和肋骨应力有不同程度的降低。因此,当肋骨侧倾损伤后,在分析潜艇的剩余强度时,应主要关注损伤肋骨附近跨中壳板的中面环向应力。
2.2 肋骨侧倾数目对应力的影响表2列出了多根肋骨向右侧倾30°时,损伤肋骨根部内表面纵向应力。可见,损伤变形肋骨根部壳板内表面纵向应力较变形前均有所降低,且最右侧一根变形肋骨根部的壳板内表面纵向应力最低,其余变形肋骨根部内表面纵向应力基本相当。
|
|
表 2 不同损伤肋骨数目时壳板内表面纵向应力计算结果 Tab.2 Calculation results of longitudinal stress on inner surface of shell with different numbers of ribs damaged |
表3列出了多根肋骨侧倾30°时,变形肋骨附近跨中壳板中面环向应力峰值。可见,变形肋骨附近跨中壳板中面环向应力较肋骨变形前提高,随着变形肋骨数目的增多,应力峰值基本相当。
|
|
表 3 不同损伤肋骨数目时壳板中面环向应力计算结果 Tab.3 Calculation results of circumferential stress of middle surface of shell with different numbers of damaged ribs |
肋骨侧倾损伤变形后,其径向刚度降低,从而环肋圆柱壳稳定性降低。表4列出了10号肋骨不同角度变形损伤时,舱段总体失稳临界压力和肋骨间壳板失稳临界压力计算结果。图8和图9为计算模型失稳后的变形云图,图10和图11为失稳临界压力变化曲线。
|
|
表 4 不同肋骨侧倾角度下失稳临界压力汇总 Tab.4 Summary of critical bucking pressures at different inclination angle of rib |

|
图 8 肋间壳板失稳变形 Fig. 8 Deformation of instability of shell between ribs |

|
图 9 总体失稳变形 Fig. 9 Deformation of overall instability |
|
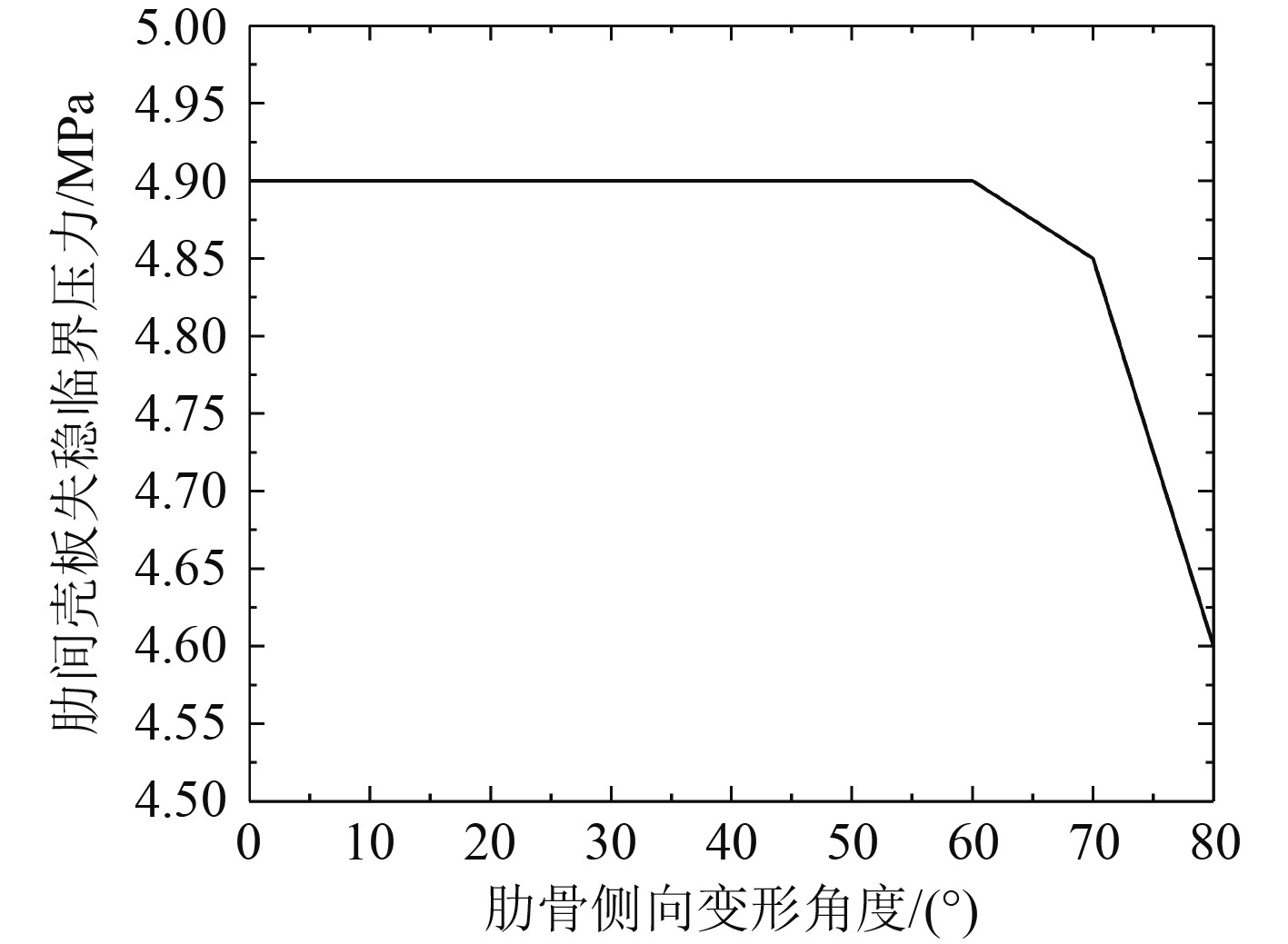
图 10 肋间壳板失稳临界压力变化曲线 Fig. 10 Critical Pressure of instability of shell between ribs |
|
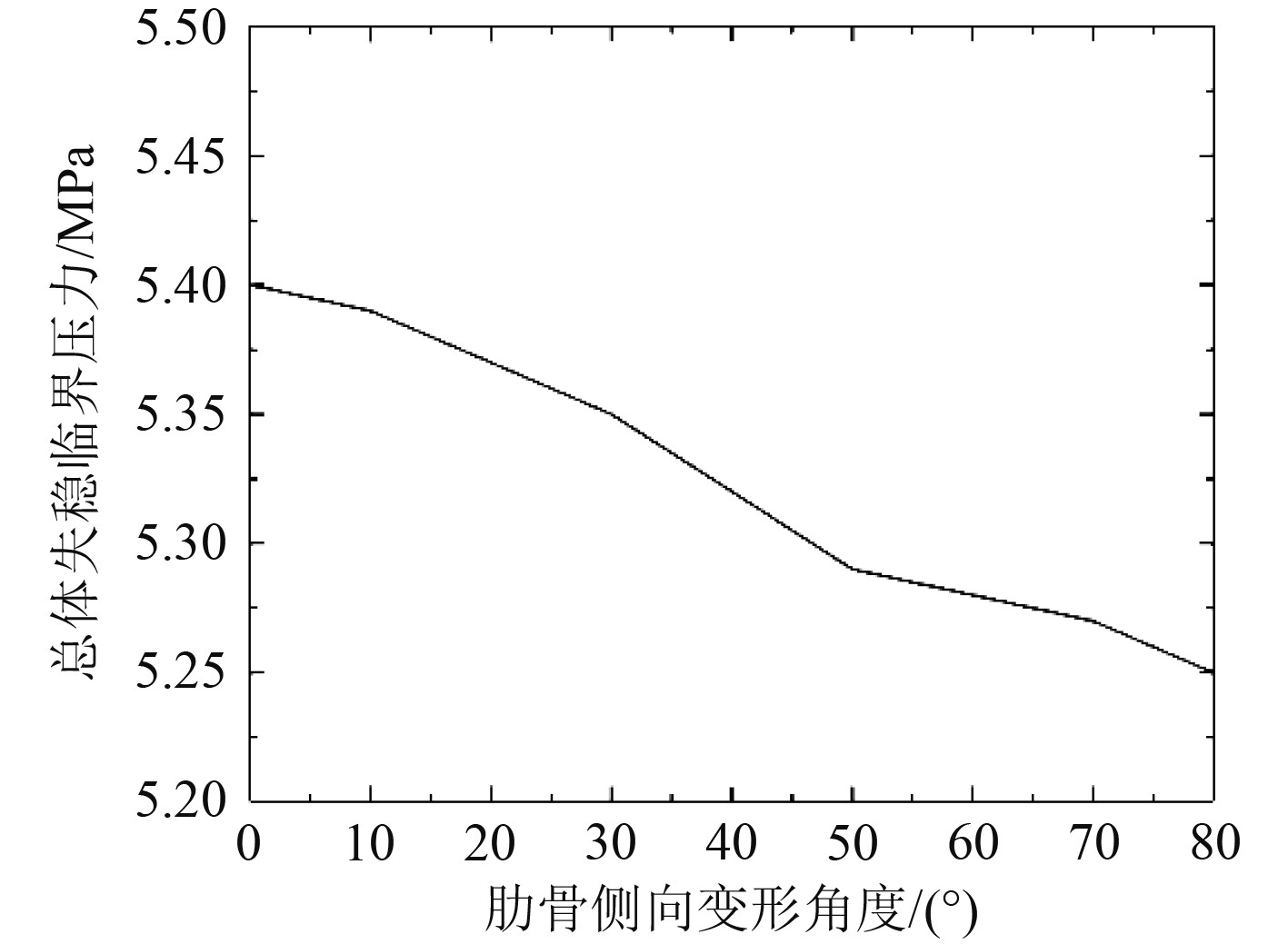
图 11 总体失稳临界压力变化曲线 Fig. 11 Critical Pressure of overall instability |
由表4可知,随着10号肋骨侧倾角度的增加,肋骨间壳板稳定性和舱段总体稳定性均降低。由图10和图11可知,随着肋骨侧倾角度的增加,肋骨间壳板失稳临界压力缓慢下降;舱段总体稳定性的变化分2个阶段:当肋骨损伤变形小于60°时,总体失稳临界压力变化较小;当变形角度超过60°后,总体失稳临界压力迅速下降。
3.2 损伤变形肋骨数目对稳定性的影响固定侧倾角度,变化侧倾肋骨数目,对计算模型的稳定性进行计算,表5为计算结果。
|
|
表 5 不同侧倾肋骨数目时失稳临界压力计算结果 Tab.5 Calculation results of critical bucking pressures of instability with different numbers of ribs damaged |
由表5可知,当侧倾角度较小时,随着侧倾肋骨数目的增加,肋骨间壳板稳定性的计算值保持不变,这是因为在进行肋骨间壳板稳定性计算时,将肋骨视作刚性约束,侧倾肋骨的增加并不会改变肋骨间壳板稳定性;当侧倾角度较大时,由于肋骨径向刚度降低严重,侧倾肋骨数目增加时,肋骨间壳板失稳的模态并未出现,此时舱段总体稳定性低于肋骨间壳板稳定性。随着侧倾肋骨数目的增加,舱段总体稳定性逐渐降低,且侧倾角度越大,侧倾肋骨数目对总体稳定性的降低就越严重。由此可见,肋骨侧倾损伤后,对舱段总体稳定性影响较大。
4 肋骨侧倾损伤后耐压艇体极限承载能力分析 4.1 损伤肋骨侧倾角度对极限承载能力的影响研究表明[12],整体特征值屈曲形态在几种主要的初挠度形式中,对结构强度的影响最不利,故本文将特征值屈曲的第一阶总体失稳模态变形作为结构初始缺陷,用弧长法得到结构的极限载荷。变化10号肋骨侧倾角度,计算舱段模型的塑性极限载荷,表6列出了一根肋骨侧向损伤、不同变形角度时,舱段模型极限载荷的计算结果,图12为极限载荷的变化曲线。
|
|
表 6 肋骨侧倾不同角度时极限强度 Tab.6 Ultimate strength with different inclination angle of rib |

|
图 12 不同肋骨侧倾变形角度下模型的极限强度 Fig. 12 Ultimate strength of the model at different inclination angle of rib |
由表6可知,随着肋骨侧倾角度的增加,舱段模型的极限承载能力逐渐降低,当侧倾角度达到30°时,耐压壳体极限承载能力降低1.7%;当侧倾角度达到60°时,耐压壳体极限承载能力降低5.4%;当侧倾角度达到80°时,耐压壳体极限承载能力降低38%。由图12可知,一根肋骨发生侧倾损伤,角度在0°~60°,极限强度随变形角度增大而逐渐减小,但下降幅度较小;角度大于60°时,肋骨起到的支撑作用越来越弱,极限强度随着侧倾变形角度的增加而急剧下降。图13和图14分别为一根肋骨侧向倾斜30°和倾斜70°时,舱段模型达到极限状态时的变形形式。当变形角度为30°时,舱段模型的破坏模式为总体失稳,总体失稳波形的范围为整个模型;当变形角度增加到70°时,舱段模型的破坏模式依然为总体失稳,此时不仅极限强度降低,极限状态时总体失稳波形仅限制在损伤变形肋骨附近。可见,大角度的肋骨变形损伤,不仅降低了结构的极限强度,还改变了结构的破坏形态。

|
图 13 肋骨侧倾30°舱段极限状态时的变形形态 Fig. 13 Deformation pattern of cabin at limit state with 30° inclination of rib |

|
图 14 肋骨侧倾70°舱段极限状态时的变形形态 Fig. 14 Deformation pattern of cabin at limit state with 70° inclination of rib |
一根肋骨出现大角度侧倾损伤,潜艇剩余强度严重降低,所以当肋骨出现大角度侧倾损伤后,潜艇应及时拖回修理,避免水下航行。现对小角度侧倾变形情况下,侧倾肋骨数目对耐压壳体极限强度的影响进行计算和分析。假设肋骨侧倾30°,改变侧倾肋骨数目,分析计算舱段模型极限承载能力,结果如表7所示。可知,随着侧倾损伤肋骨数目的增加,舱段极限强度逐渐降低,变化趋势接近线性。
|
|
表 7 不同侧倾肋骨数目舱段模型的极限强度 Tab.7 Ultimate strength of cabin with different numbers of ribs damaged |
潜艇耐压艇体肋骨出现侧倾损伤后,其强度、稳定性和极限强度都有所降低,可以依据下式确定潜艇的极限下潜深度:
| $ {H_{sy}} = \min \left( {{H_{sy - 1}},{H_{sy - 2}},{H_{sy - 3}},{H_{sy - 4}}} \right),$ |
| $\begin{split} &{H_{sy - 1}} = \frac{{\sigma _2^0}}{{\sigma _{2{\text{ - s}}}^0}}{H_{jx}}\text{,}{H_{sy - 2}} = \frac{{{P_{cr - s}}}}{{{P_{cr}}}}{H_{jx}}\text{,}\\ &{H_{sy - 3}} = \frac{{P_{_{cr - s}}'}}{{P_{cr}'}}{H_{jx}}\text{,}{H_{sy - 4}} = \frac{{{P_{jx - s}}}}{{{P_{jx}}}}{H_{jx}} 。\end{split}$ |
其中:Hjx为潜艇的设计极限下潜深度;
以10号肋骨侧倾变形为例,损伤后计算模型的剩余下潜深度系数如表8所示。
|
|
表 8 一根肋骨侧倾损伤后计算模型的剩余极限下潜深度系数 Tab.8 Residual limiting depth coefficient of model with one rib damaged |
针对潜艇耐压艇体肋骨侧倾损伤,采用控制变量的方法,通过改变损伤肋骨侧倾角度、侧倾肋骨数目,分析比较了结构的应力、稳定性和极限承载能力,得到结论如下:
1)随着肋骨侧倾角度的增大,损伤肋骨附近跨中壳板中面环向应力逐渐增大,损伤肋骨根部壳板内表面纵向应力和肋骨应力逐渐减小。跨中壳板中面环向应力是控制潜艇剩余下潜深度的应力指标。
2)肋骨损伤变形后,舱段总体稳定性显著降低,肋骨间壳板稳定性变化较小。舱段总体稳定性是控制潜艇剩余下潜深度的稳定性指标。
3)肋骨侧向损伤变形角度和变形肋骨数目增加,均降低结构的极限强度,但侧倾角度会带来更为严重的强度不足。
4)通过对损伤后耐压艇体的应力、稳定性和极限强度的计算,可以反推潜艇的剩余极限下潜深度,从而为潜艇损伤后短时的使用提供技术支持。
| [1] |
SURKO S W. Crushing strength of box columns with partially-damaged plating[J]. Pergamon, 1991, 33(12): 1017−1028.
|
| [2] |
PAIK JK, THAYAMBALLIA K, YANG SH. Residual strength assessment of ships after collision and grounding[J]. Marine Technology, 1998, 35(1): 38-54. |
| [3] |
NIESSEN E,. Structural design for enhanced survivability of ship's hulls[J]. Iongitudinal Strength, 1991.
|
| [4] |
NOTARO G, KIPPENES J, AMLASHI H, et al. Residual hull girder strength of ships with collision or grounding damages[C]// 11th Inte. Symp. on Practical Design of ships and Other Floating Structures. Rio, Brazil, 2010.
|
| [5] |
高本国. 船体极限强度与破损剩余强度非线性有限元分析[D]. 武汉: 武汉理工大学, 2012.
|
| [6] |
李晨鹏, 岳亚霖, 李永正, 等. 含裂纹损伤的舱段剩余极限强度研究[J]. 舰船科学技术, 2019, 41(3): 25-30+49. LI Chen-peng, YUE Yalin, LI Yong-zheng, et al. Research on residual ultimate strength of cabin with crack damage[J]. Ship Science and Technology, 2019, 41(3): 25-30+49. |
| [7] |
白雪飞, 郭日修, 赵海江. 受损伤潜艇结构剩余强度评估[J]. 船舶力学, 2012, 16(Z1): 118-126. BAI Xue-fei, GUO Ri-xiu, ZHAO Hai-jiang. Evaluation of residual strength of damaged submarine structure[J]. Journal of Ship Mechanics, 2012, 16(Z1): 118-126. |
| [8] |
梅志远, 李卓, 吕岩松. 单/双壳体潜艇结构耐撞剩余强度特性研究[J]. 中国舰船研究, 2011, 6(5): 7-10. MEI Zhi-yuan, LI Zhuo, LV Yan-song. Research on crashworthiness residual strength characteristics of single/double hull submarine structure[J]. China Ship Research, 2011, 6(5): 7-10. DOI:10.3969/j.issn.1673-3185.2011.05.002 |
| [9] |
马晓龙, 吴梵, 张二. 点蚀损伤对环肋圆柱壳极限强度的影响[J]. 船海工程, 2018, 47(1): 29-32+37. DOI:10.3963/j.issn.1671-7953.2018.01.007 |
| [10] |
吕岩松, 吴龙祥. 局部损伤环肋圆柱壳的强度分析和加强方案[J]. 舰船科学技术, 2013, 35(8): 62-65. DOI:10.3404/j.issn.1672-7649.2013.08.014 |
| [11] |
袁伯伟. 潜艇不垂直肋骨的强度计算[J]. 舰船科学技术, 1984(11): 37-52+84. |
| [12] |
THEODORE, V, KÁRMÁN. The engineer grapples with nonlinear problems[J]. Bulletin of the American Mathematical Society, 1940, 46.
|
 2022, Vol. 44
2022, Vol. 44

