近年来,随着国际海事组织对节能环保要求的提高和船东对于节能的需求,双燃料系统越来越多的运用在船舶运营中。丁惊雷[1]分析了双燃料主机的应用对船舶总体设计的影响,应用双燃料主机能够有效降低EEDI指数,但必须考虑LNG罐在主甲板的布置。本文研究对象为一艘21万吨级的双燃料散货船,因此在线型优化设计中要保证LNG罐的布置要求。
基于计算流体动力学(CFD)的船舶线型优化已成为常用的手段,船舶工程师通常采用母型变换法、经验设计或参数化设计来获得优化线型,结合CFD方法进行快速性能的评估,最终获得优化方案[2-4]。船型变换是船型优化设计的首要环节,意大利INSEAN水池在基于SBD技术的船舶水动力性能优化设计方面开展了大量的研究工作,对船体几何重构技术进行了较为系统的研究[5]。万德成[6]总结了船型变换技术的研究进展,介绍了近年来较为常用的几种船型变换方法:NURBS法、平移法、自由变形法、径向基函数法、正交基函数叠加法。李胜忠[7]基于FFD自由变形技术实现了船体整体与局部的同时变形。赵无忧[8]通过径向基插值技术实现船体自动变形,通过Shipflow软件进行水动力计算,成功优化了隐形球首散货船的兴波阻力。上述文献表明,船型自动变换方法越来越多的应用到船型优化工作中,能够有效提升船型优化效率和质量。
本文基于修正函数法[9]实现了21万吨级散货船的船型变换,结合CFD评估方法,对首部兴波、总阻力和推进性能进行优化,并与模型试验结果进行比对和验证,证明了该船型优化设计方法的有效性和可靠性。
1 优化方法 1.1 船体线型变形方法采用基于修正函数的参数化船型自动变形和重构方法[9],从数学上看,该方法的基本思想是建立一个从待变形几何曲面空间到目标几何曲面空间的三维映射,采用参数化的转换函数,求出的几何变形量并叠加到初始几何曲面上,从而得到新的船型曲面的变形方法。其表达式如下:
| $ {H_{new}}\left( {x,y,z} \right) = {H_{old}}\left( {x,y,z} \right) + \Delta H\left( {x,y,z} \right) 。$ | (1) |
其中,
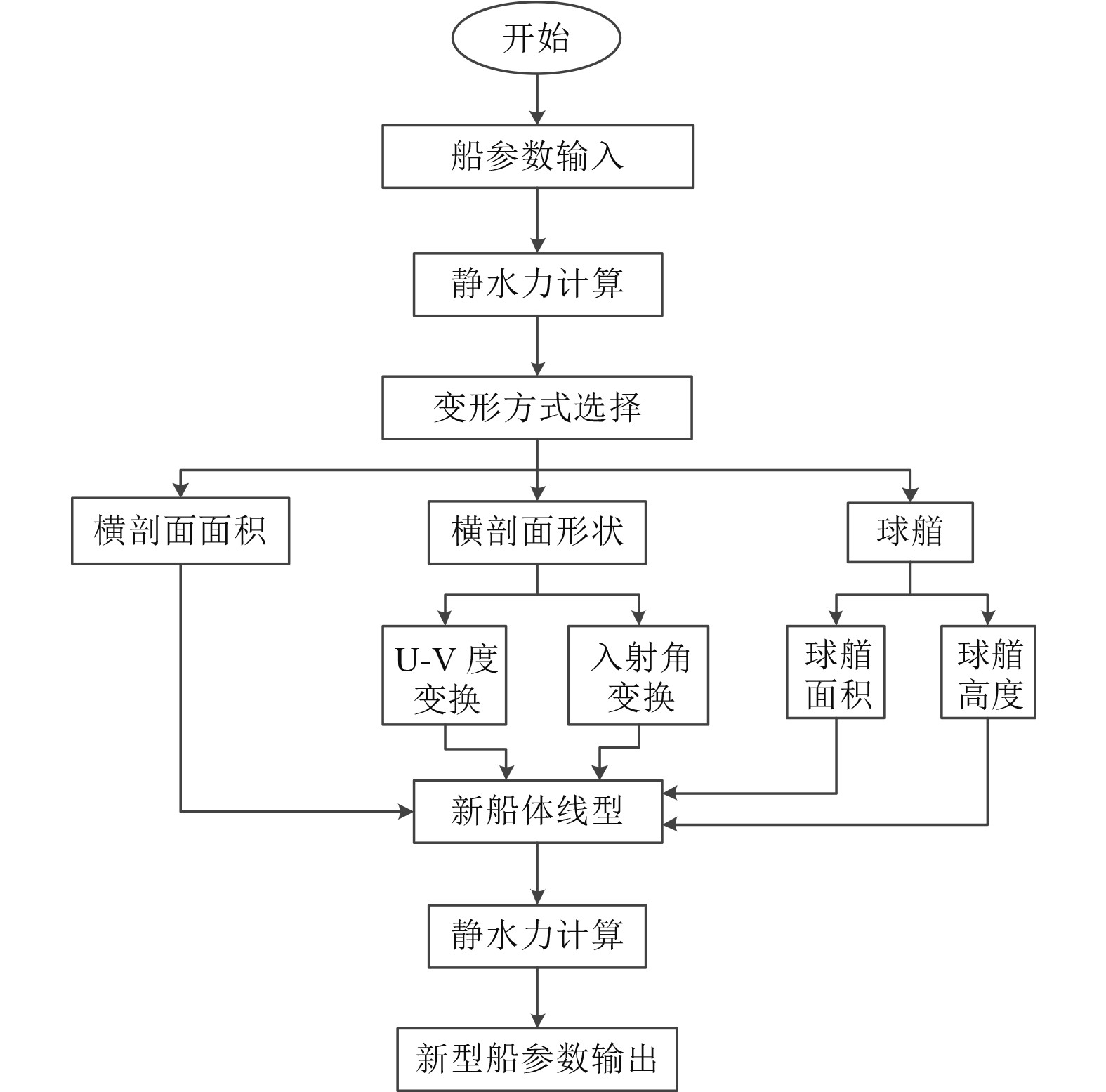
冯君[9]基于该船体线型自动变形方法,开发了船体线型自动变形程序。该程序主要包括:现有船型(母型)参数输入、静水力性能计算、船体线型变形、新船型参数输出。流程如图1所示,可以在排水量和方形系数变化较小的情况下,同时保证船体线型的光顺性,实现船型局部或整体的变形,满足船型优化设计者对船型局部或整体优化变形要求,具有很好的可行性和适应性。同时,大大减少了船体建模的工作量,提高了船型优化的效率。
|
图 1 船体线型自动变形程序流程图 Fig. 1 Flow chart of hull line automatic deformation program |
本文采用快速CFD模拟方法[10]。该方法的基本思路是根据流动特点将船体分为3部分求解:第一部分采用非线性兴波数值计算方法,第二部分求解边界层上的积分方程,第三部分则通过求解RANS方程获得船尾的流场。
1.3 船型优化流程结合船体线型自动变形程序和CFD评估方法,实现21万吨散货船的船型优化。把优化对象的原始线型称作初始线型,优化流程如图2所示。

|
图 2 船型优化流程 Fig. 2 Ship form optimization process |
考虑到兴波阻力、总阻力、推进性能的CFD评估耗时依次增加,为了节省计算时间,提高优化效率,首先进行兴波阻力的优化,获得兴波阻力性能较优的方案。在此基础上,再次进行总阻力和推进效率的优化,最终获得综合性能最优的方案。
2 研究对象本文研究对象为1艘21万吨级双燃料散货船,其主尺度如表1所示。
|
|
表 1 船型主尺度参数表 Tab.1 Parameters of ship |
同时,由于双燃料主机的特殊性,在线型优化时要考虑到LNG罐的布置要求。因此,在优化设计过程中,控制船尾主甲板线型不变,即图3中的所圈区域在线型变换中保持不变。

|
图 3 船体三维示意图 Fig. 3 3D schematic diagram of hull |
分别对首部和尾部进行船型优化。应用船体线型自动变形程序,对船体的首部和尾部线型进行改型,图4为首部和尾部主要变形区域的横剖面示意图。

|
图 4 首部和尾部主要变形区域的示意图 Fig. 4 Schematic diagram of main deformation areas of bow and stern |
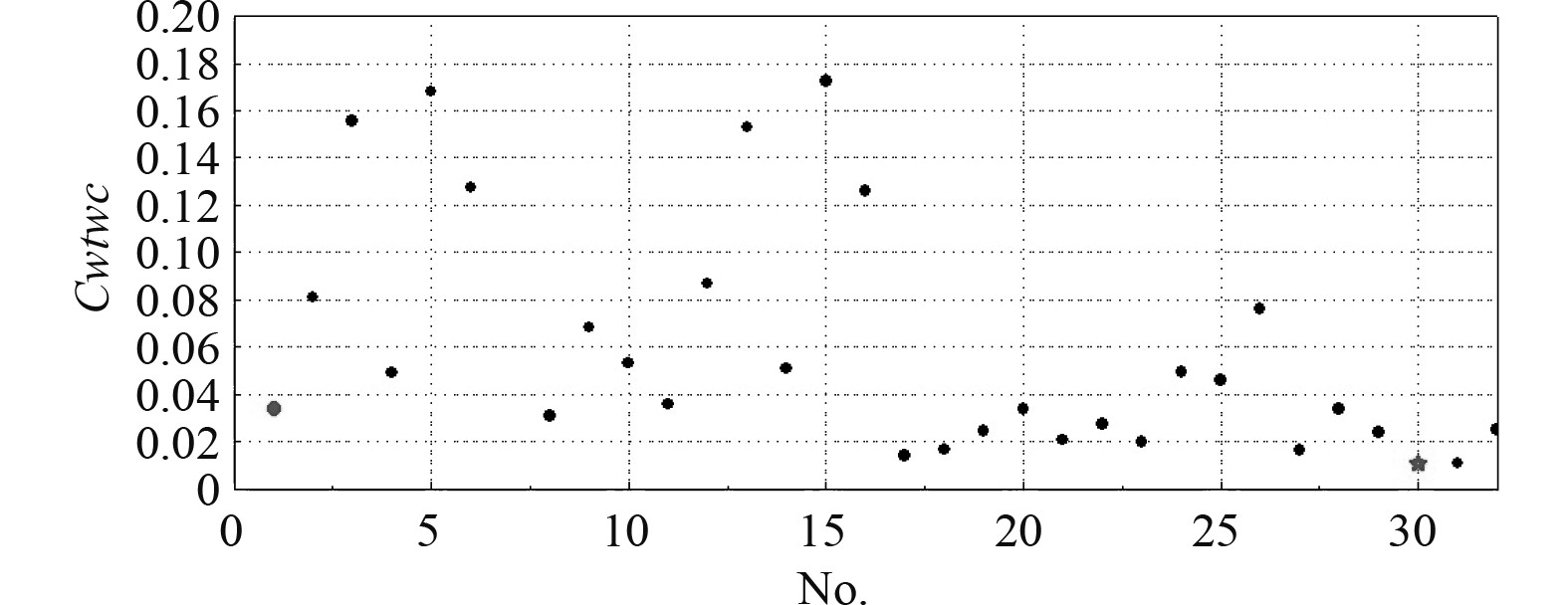
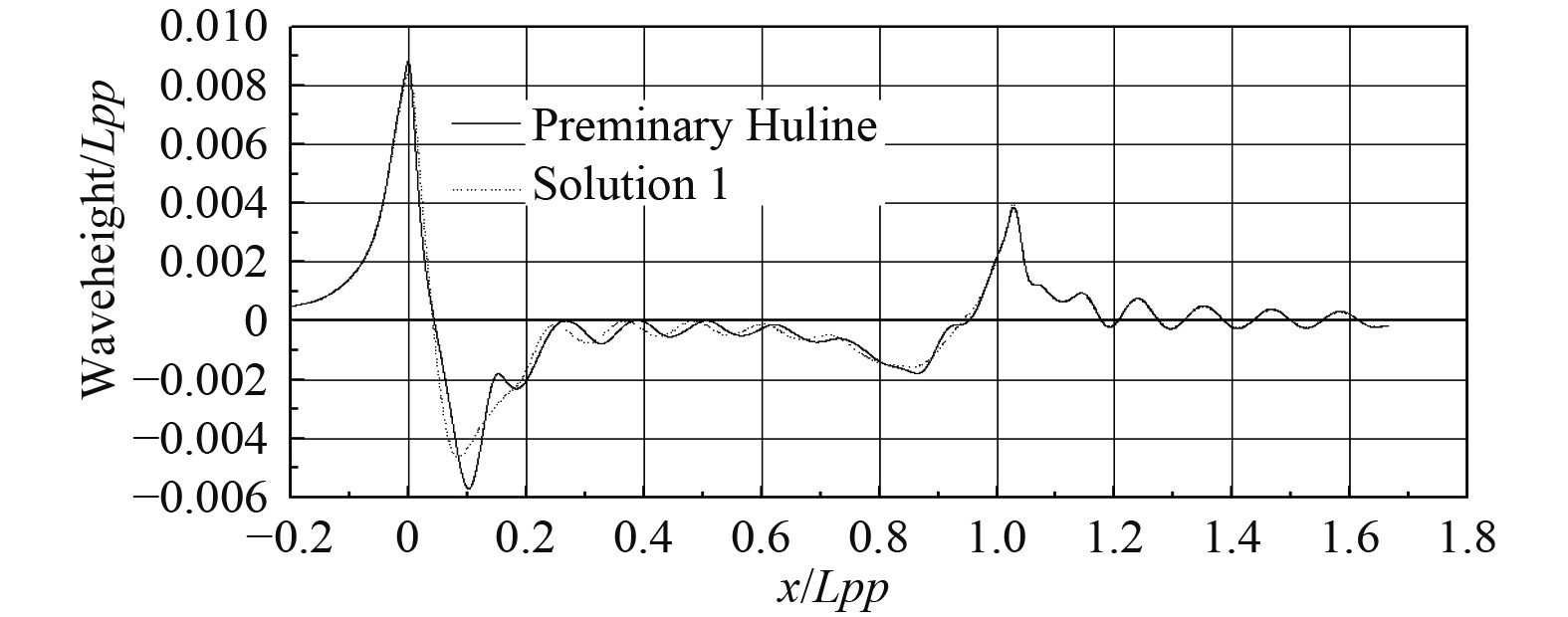
结合专家经验,水线附近的线型对兴波阻力影响较大。在初始线型的基础上,对水线附件线型(图4中的1号区域)进行自动变换,并对兴波阻力进行CFD评估,舷侧兴波积分系数如图5所示。经过挑选,选择舷侧兴波积分系数最优的方案作为方案1。图5中,圆点和五角星分别表示初始线型和方案1的兴波评估结果。初始线型和方案1的舷侧波形如图6所示,方案1的船首波谷较初始线型抬高,波形也更加平缓。
|
图 5 变形方案兴波阻力大小汇总图 Fig. 5 Summary diagram of wave resistance |
|
图 6 初始线型和方案1的舷侧波形对比图 Fig. 6 Comparison diagram of shipboard waveform between initial line type and scheme 1 |
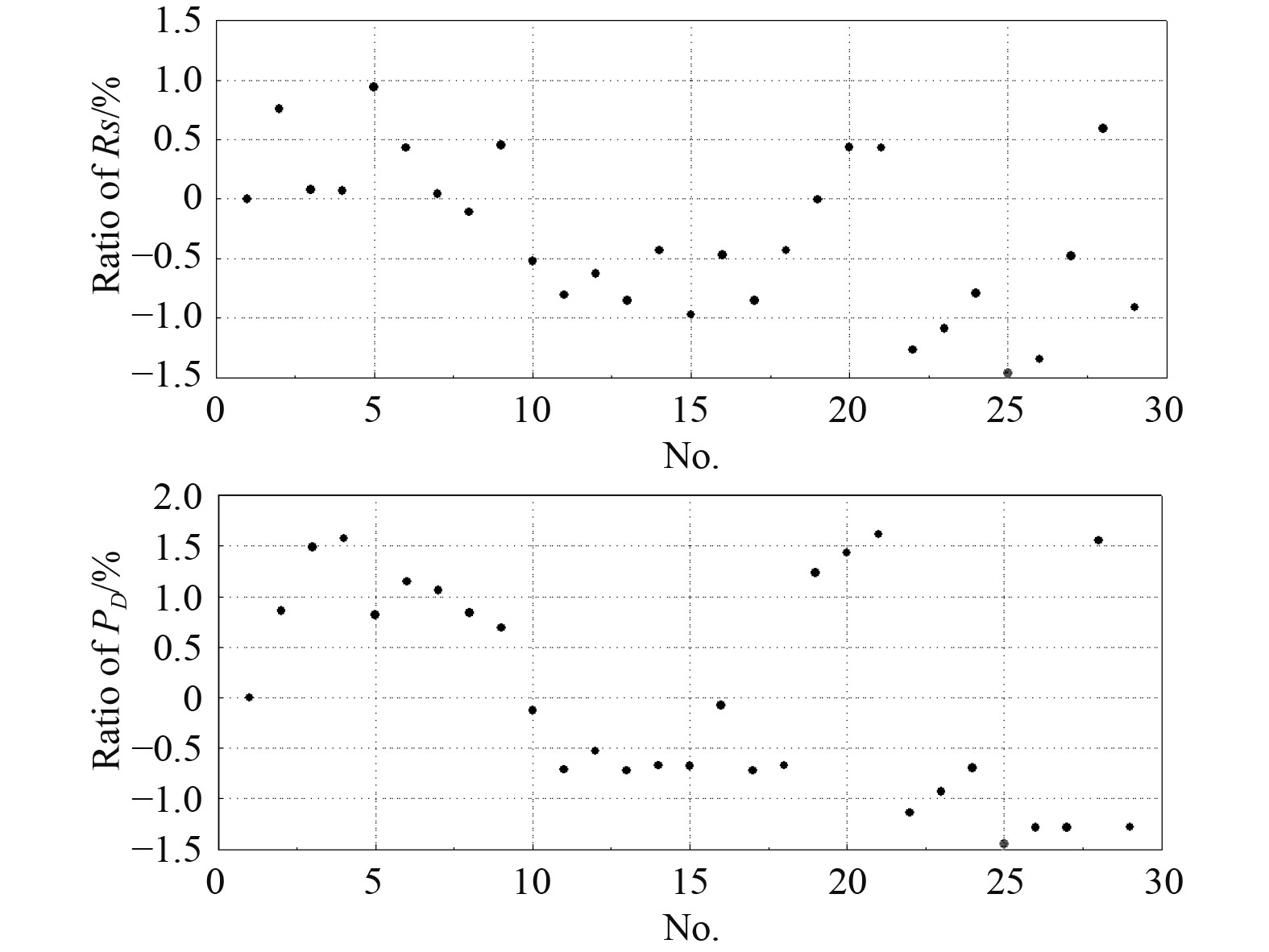
根据杨佑宗[11]的研究,船尾整流穴(图4中3号位置)线型对阻力和推进效率的影响较大,在方案1的基础上,控制船尾主甲板附近线型(图4中2号位置)不变的情况下,对该位置的线型进行自动变换,筛选出满足机舱布置限制要求的方案,对这些方案的阻力和推进性能进行CFD评估。图7为在18.4 m吃水和设计航速(
|
图 7 各方案阻力和推进性能汇总图 Fig. 7 Summary diagram of resistance and propulsion performance of each scheme |
可以看出:多数优化方案的阻力和收到功率相对初始线型方案有所降低;相对于初始线型方案,最终方案在设计航速下的模型阻力减小了1.464%,收到功率下降了1.448%,快速性能收益十分显著。
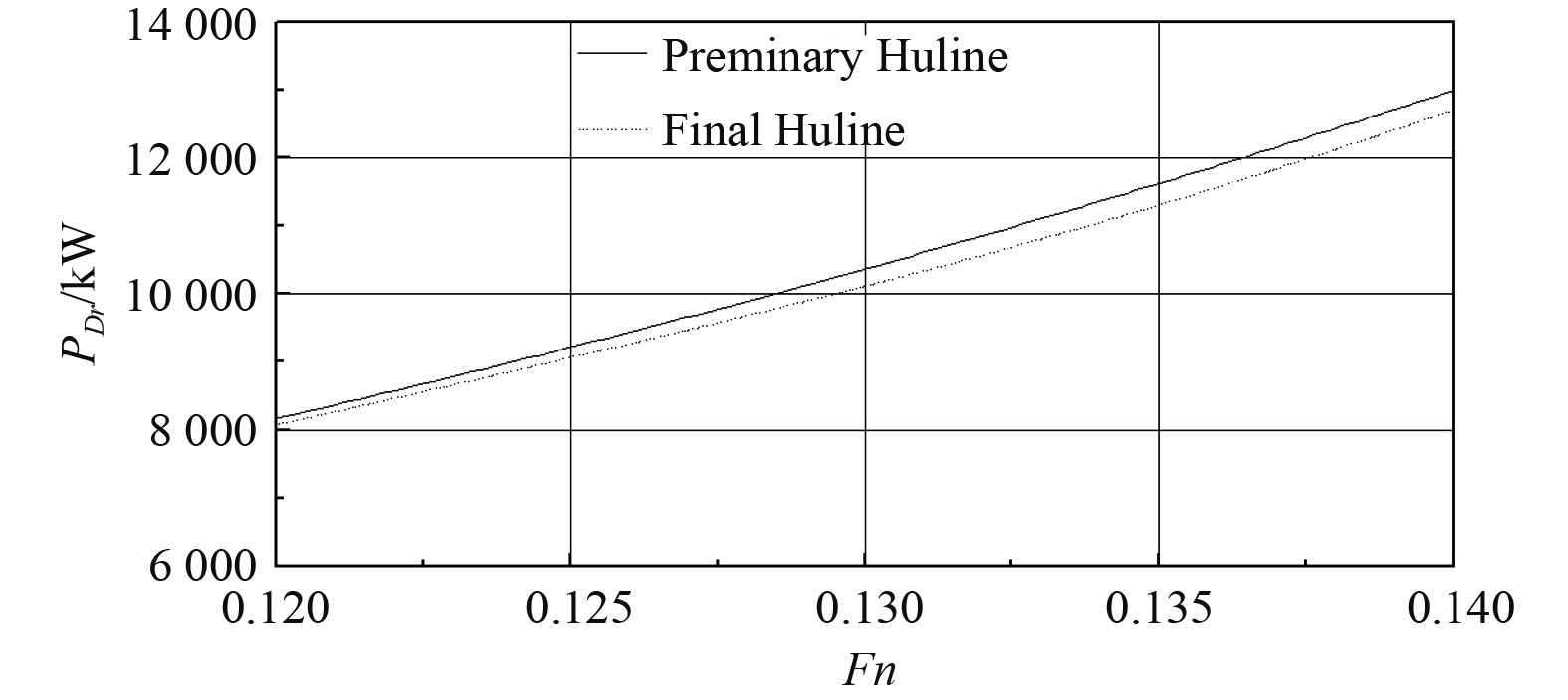
4 模型试验验证为了验证上述优化设计结果的可靠性,在拖曳水池同时开展初始线型和最终方案的快速性模型试验,模型试验结果及其比较如图8所示。
|
图 8 初始线型和最终方案模型试验收到功率对比图 Fig. 8 Comparison diagram of PD (model test) of preliminary and final hull line |
从最终方案和初始线型模型试验阻力和收到功率(均换算到15℃海水条件下)的对比结果可以看出:与初始线型相比,最终方案的收到功率在整个航速段上均有减小;在设计航速Fn=0.133附近,收到功率减小最为显著,较初始线型降低约3%。试验结果充分验证了该21万吨级双燃料散货船船型优化设计的成功,同时说明了该船型优化方法的有效性和可靠性。
5 结 语1)结合基于修正函数的船体线型自动变形技术与 CFD 数值评估技术,建立了高效船型设计方法。该方法成功实现了船体线型的快速变形,与传统的手动修改线型相比,节省大量时间,能获得更多数量的线型方案,提高了船型优化效率的同时达到性能指标要求。
2)以1艘21万吨级双燃料散货船作为设计对象,设计吃水和设计航速工况下的快速性能作为优化目标,采用船型自动变形程序和 CFD 评估方法对其整体线型进行优化设计。结果表明:在满足工程约束条件下,最终方案快速性能收益十分显著,设计航速时模型总阻力降低了1.464%,推进效率提高了1.448%。
3)为了验证优化设计效果,分别开展了初始方案与最终方案快速性模型试验。试验结果表明:在设计吃水下,相对初始方案,最优方案整个航速范围内,收到功率均有降低,在设计航速附近最为显著,收到功率下降了约3%。该结果和数值优化计算结果的变化趋势基本吻合,充分验证了本文船型优化设计方法的有效性和可靠性。
| [1] |
丁惊雷, 吴思莹. 双燃料应用对大型油船总体设计的影响[J]. 船舶工程, 2021, 43(5): 39-43. |
| [2] |
CAMPANA E F, PERI D, TAHARA Y, et al. Numerical optimization methods for ship hydrodynamic design[J]. Transactions-Society of Naval Architects and Marine Engineers, 2010, 118: 1−42.
|
| [3] |
万德成, 缪爱琴, 赵敏. 基于水动力性能优化的船型设计研究进展[J]. 水动力学研究与进展, 2019, 34(6): 693-712. |
| [4] |
陈京普, 朱德祥, 何术龙, 等. 一种快速评估方法在船舶线型优化中的应用研究[J]. 中国造船, 2009, 50(4): 7-12. DOI:10.3969/j.issn.1000-4882.2009.04.002 |
| [5] |
陈京普, 朱德祥, 黄少锋. 基于兴波数值模拟的 RANS 求解器加速方法研究[J]. 船舶力学, 2011, 15(Z1): 25-31. |
| [6] |
CHEN Jing-pu, WEI Jin-fang, JIANG Wu-jie. Optimization of a twin-skeg container vessel by parametric design and CFD simulations[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8(5): 466-474. DOI:10.1016/j.ijnaoe.2016.05.008 |
| [7] |
李胜忠, 徐伟光, 梁川, 等. 船舶规则波中阻力与运动响应多目标优化设计研究[C]//2019年中国造船工程字会优秀学术论文集, 2020: 218−226.
|
| [8] |
赵无忧, 郭啸轩. 基于CFD的散货船船体型线自动优化[J]. 江苏船舶, 2019, 36(4): 8-11. |
| [9] |
冯君, 胡世亮, 魏锦芳. 基于修正函数方法的船体线型变形技术研究[C]//第二十九届全国水动力学研讨会论文集(下册), 2018: 449-456.
|
| [10] |
LARSSON L. CFD in ship design-prospects and limitati-onsl[J]. Ship Technology Research, 1997, 44: 1-30. |
| [11] |
杨佑宗, 杨奕, 陈文炜, 等. 船舶线型设计与研究[J]. 上海造船, 2001(2): 18-23+2. |
 2022, Vol. 44
2022, Vol. 44
