0 引　言

船舶在海上航行过程中，面临复杂多变的海上环境，通信的重要性逐渐显露出来^[1]。现代船舶航行已经无需人工驾驶，只需要专业人员控制数控设备，就能实现船舶的控制航行，航行规划、故障识别、动力控制都可以通过船舶自身的控制系统，经通信传输渠道实现控制，保证船舶的平稳航行^[2-4]。只有合理调度船舶网络，实现整体控制系统的操控，才能确保船舶稳定、正常在海面上安全航行。调度被广泛应用于交通通信的领域之中，调度会结合计算机科学、人工智能技术、生产管理科学等多个领域的技术，实现综合统筹应用^[5]。在船舶控制系统中，通过网络实现整个船舶数据信息的共享与管理，确保船舶的高效运行。

目前已经有众多研究者在船舶网络优化调度方面作出研究，鲍劲松等^[6]提出以遗传算法作为基础，优化调度网络，但是由于容易过早陷入最优解，导致优化调度效果不尽如人意。徐诗鸿等^[7]提出基于模拟退火算法的船舶网络优化调度，但是模拟退火算法的优化效率较差，所以调度效果仍旧需要进一步研究。

本文研究改进遗传算法的船舶网络优化调度方法，通过网络调度实现报文传输抖动最小，并利通过改进遗传算法，提升遗传算法的搜索效率，获得最佳调度结果。

1 改进遗传算法的船舶网络优化调度 1.1 基于高层控制器局域网络协议的船舶网络结构 1.1.1 高层控制器局域网络协议分析

本文所研究的船舶网络是一种高层控制器局域网络（TT controller area network,TTCAN）协议，作为一种高层的协议，TTCAN已经将CAN总线内的全部信息实现通信，同时将全网络的虚拟时钟展现出来^[8-9]。网络中的数据传输需要一个特定的时间窗口，同时管理并预测网络上的信息。以时间作为判断依据TTCAN上有一个主节点，利用计数器实现节点时间副本完整存储，计数器间隔1个单位累加1个点。

TTCAN组成结构包含时间槽与时间窗口，单个信息经时间窗口就能完成在网络中节点的传输^[10]。TTCAN内具有矩阵周期，矩阵周期的起、始分别为同步信息初始发布与第2个信息出现的点。船舶网络的通信调度结构由矩阵周期决定，网络中调度的未来发展由周期性执行矩阵周期确定，帮助优化调度结果适用于船舶网络。

1.1.2 船舶网络拓扑结构

使用模拟退火遗传算法优化TTCAN内的矩阵周期，确保船舶网络内的报文信号具有最低传输抖动。船舶正常运行需要多个控制网络支持，包括数个子控制网络，这些子控制网络共同运作形成一个总的控制网络，实现船舶的航行控制，指令一旦发出，相关设备具有在规定时间之内作出响应，否则影响船舶正常航行，出现重大安全事故^[1]。

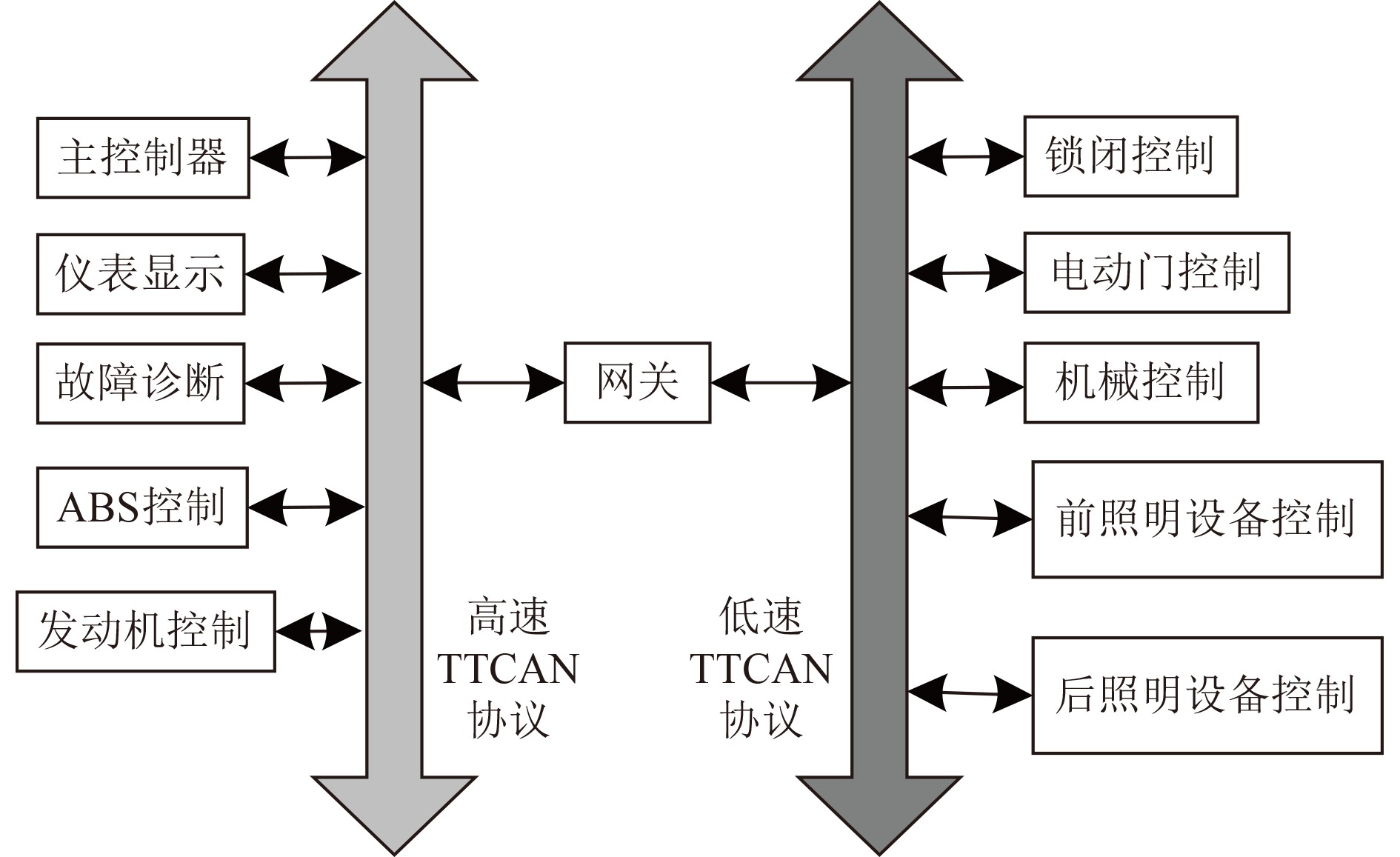
船舶的控制网络中，不同节点对于报文传输时效的要求不同，从这一角度出发，选取高速和低速2种TTCAN协议构建整个船舶控制网络的拓扑结构（见图1）。

1.2 模拟退火遗传算法的船舶网络矩阵优化调度 1.2.1 船舶网络优化调度目标

船舶控制TTCAN网络内的矩阵周期分为节点传输周期与非周期2种不同的报文信息，这2种报文的内部也各自存在差异：周期性报文历次传输过程中，所设定的周期存在差异；传输时间方面，非周期性报文无法确定标准，这种情况造成实例存在差异关系的情况下，即使是相同周期性报文，会出现周期与时间间隔不对等的情况，也就是说，船舶控制网络之中的报文传输实际时刻与预计时刻之间出现显著差值，这种差值在船舶网络优化调度过程中被称为报文传输抖动，通过下式表示：

$ {j_{i,k}} = {t_{ai,k}} - {t_{ei,k}} ，$

(1)

$ {t_{e,i,k}} = k{M_i} + {t_{0i}} 。$

(2)

其中： $ {M_i} $ 代表第 $ i $ 个报文的传输周期， $ i = 1,2,3, \cdots ,n $ ，第0个实例第 $ i $ 个报文的传输时间开端描述为 $ {t_{0i}} $ ， $ {t_{ai,k}} $ 与 $ {t_{ei,k}} $ 分别为第 $ i $ 个报文第 $ k $ 个实例实际与预计开始传输时间。

对式（1）作出分析，矩阵周期的全周期之内，使用式（3）描述船舶控制网络之中的全部报文传输抖动情况：

$ {J_{OS}} = \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^{{M_i}} {{j_{i,k}}} } 。$

(3)

船舶网络优化调度使用一种优化算法，实现报文传输抖动值最低， $ \min {J_{OS}} $ 也是船舶网络优化调度的最终目标。

1.2.2 基于模拟退火遗传算法的调度优化

遗传算法寻优能力极强，寻优过程中考虑全部种群，但是该算法寻优过程中会出现提前进入最优解的情况，出现较差搜索效率。模拟退火局部搜索能力较强，但是搜索效率较差。2种算法各有所长也各有不足，将2种算法结合到一起，模拟退火遗传算法详细步骤如下：

步骤1　给出算法参数，将退火初始温度 $ {T_i} = \inf $ 设定成一个足够大的数，进化代数 $ i $ 设定为0。

步骤2　随机生成初始化种群，设定为 $ {G_i} $ ，该种群也是通过方案部署获得的可行解集合。

步骤3　执行交叉算子和变异算子。初步筛选原始群体，利用交叉概率 $ {p_c} $ 随机选取该群体中的2个个体，交换随机部分染色体，产生2个全新的个体便是执行后的交叉算子。使用预设概率改变染色体基因叫做执行变异算子，假设在父代染色体的随机位置上发生基因变异，生成子代染色体，该染色体会替换父代染色体。执行交叉算子与变异算子的最终目的是抑制早熟收敛，随着适应值的变化，交叉概率 $ {p_c} $ 与变异概率 $ {p_m} $ 都会发生改变，如果陷入局部极值，个体中较大适应值的部分也会出现变异概率和交叉概率的增大，这样就能实现过早收敛的抑制。根据这些分析，使用式（4）和式（5）分别定义交叉概率 $ {p_c} $ 与变异概率 $ {p_m} $ ：

$ {p_c} = \left\{ \begin{gathered} {c_1}*\left[ {\left( {{f_{\max }} - f} \right)/\left( {{f_{\max }} - {f_{\min }}} \right)} \right],f \geqslant \bar f ；\hfill \\ {c_2},f < \bar f ，\hfill \\ \end{gathered} \right. $

(4)

$ {p_m} = \left\{ \begin{gathered} {c_3}*\left[ {\left( {{f_{\max }} - ff} \right)/\left( {{f_{\max }} - {f_{\min }}} \right)} \right],ff \geqslant \bar f ，\hfill \\ {c_4},ff < \bar f 。\hfill \\ \end{gathered} \right. $

(5)

式中： $ {f_{\max }} $ 与 $ {f_{\min }} $ 分别用于描述最大与最小适应值； $ \bar f $ 与 $ f $ 分别代表平均适应值与交叉个体较大适应值； $ {c_1} $ ， $ {c_2} $ ， $ {c_3} $ ， $ {c_4} $ 均属于 $ \left( {0,1} \right) $ ， $ ff $ 用于描述变异适应值，通过 $ {f_{\max }} $ 与 $ {f_{\min }} $ 之间的差值表示种群稳定性，同时也能抑制算法过早收敛，但是却不能实现优良个体保存，该差值会使 $ {p_c} $ 与 $ {p_m} $ 发生变化， $ \left( {{f_{\max }} - f} \right) $ 与 $ \left( {{f_{\max }} - ff} \right) $ 能调整该变化，实现收敛抑制与最优解寻找。

步骤4　计算适应度函数。适应度函数能够衡量寻优程度，所以恰当的适应度函数也是迭代的评估标准，将等待求解的矩阵内各报文实例的目标函数 $ f\left( x \right) $ ，向适应度函数 $ fitness\left( {f\left( x \right)} \right) $ 转化，则有下式：

$ fitness\left(f\left(x\right)\right)=\left\{\begin{array}{l}f\left(x\right)，目标函数最大化问题，\\ -f\left(x\right)，目标函数最小化问题 。\end{array} \right.$

(6)

使用式（6）获得全新种群适应度 $ F\left( {{G_i}^\prime } \right) $ 。

步骤5　使用式（7）计算退火增量：

$ \Delta F = F\left( {{G_i}} \right) - F\left( {{G_i}^\prime } \right)，$

(7)

式中， $ F\left( {{G_i}} \right) $ 表示原始种群适应度函数。假如 $ \Delta F $ 小于0，可以将 $ {G_i}^\prime $ 作为下一代种群，如果 $ \Delta F $ 不小于0，通过概率 $ \exp \left[ { - \left( {\Delta F/{T_i}} \right)} \right] $ 将 $ {G_i}^\prime $ 作为下一代种群。如果 $ {G_i}^\prime $ 不被接受成为下一代种群，跳转至步骤3，重新获得全新种群。

步骤6　退温。模拟退火算法参数见下式：

$ \left\{ \begin{gathered} {T_{i + 1}} = \lambda {T_i},0 < \lambda < 1 ，\hfill \\ {G_i} = {G_i}^\prime ，\hfill \\ i = i + 1 。\hfill \\ \end{gathered} \right. $

(8)

步骤7　对进化结束条件作出判断，如果满足结束条件就可以输出最优个体，结束计算，如果不满足结束条件需要重新跳转至步骤3，设定进化初始种群为 $ {G_i} $ 。

该算法随机生成初始化种群，并随机执行交叉与变异，获得子代个体，该个体与父代个体发生竞争，保留更加优良的个体，避免算法出现早熟情况。迭代进化的推进，温度发生下降，不会再接受劣质解，通过模拟退火算法的爬山特性使得遗传算法具有更加良好的收敛速度。

2 模拟试验

以我国自主建造的大型船舶作为研究对象，该船长度为323.6 m，船身高度为72.2 m，最大吃水量与最大航速分别为8.55 m与22.6 kn/h。收集该船舶控制网络的相关数据参数，设定255 kbit/s是报文传输速率。使用模拟试验平台根据这些数据开展模拟试验，验证本文方法的性能。

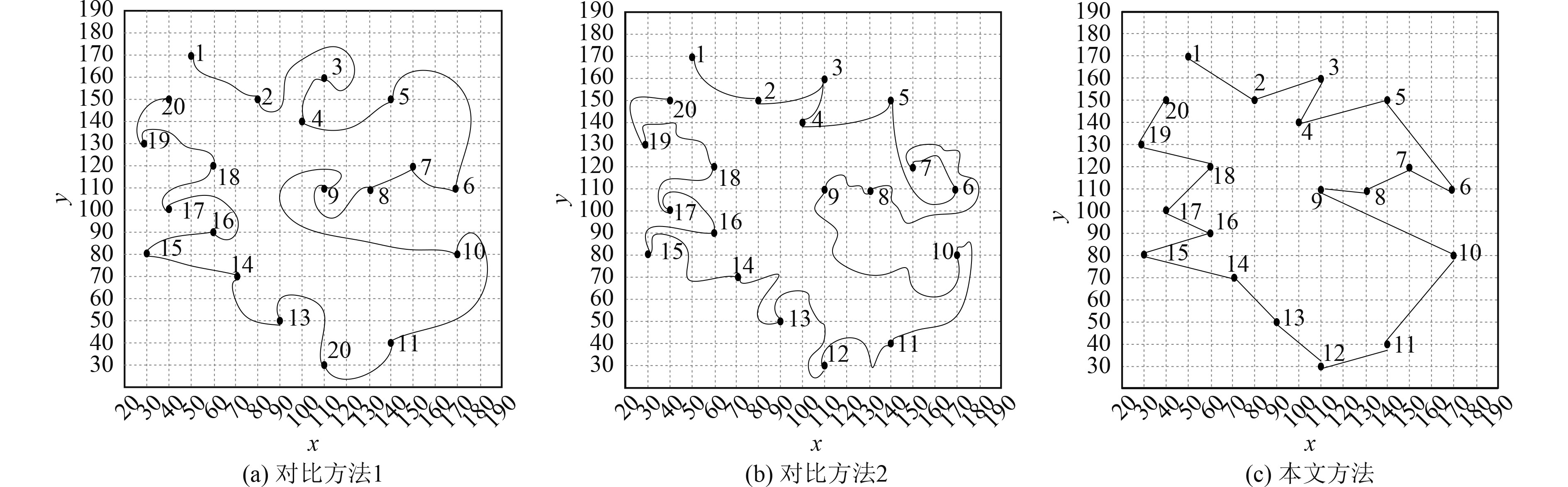
2.1 算法性能验证

假设模拟试验平台中存在20个网络节点，报文信息在各个节点之中传输。本文方法综合遗传算法与模拟退火算法的优点，最终实现船舶网络优化调度，因此试验过程中，同时使用基于遗传算法的调度方法（参考文献[6]，下文简称对比方法1）和基于模拟退火算法的调度方法（来自参考文献[7]，下文简称对比方法2）调度船舶网络，不同算法调度之下，报文信息的传递轨迹如图2所示。图中数字表示网络节点的编号，数字1是报文传输的起始节点，数字20是报文传输的终点节点。能够看出，相比于2种未改进的方法，本文方法在报文传输过程中能够获得最短传输路径，报文传输速度较快，而2种对比方法传输报文时路径较远，容易造成延误报文传输的局面。

2.2 网络优化调度性能测试

在模拟试验平台中模拟船舶在正常天气环境下，无干扰时实际行驶中较为关键的各个子控制网络状态，使用本文方法以及2种对比方法对船舶网络优化调度后，各子网络中报文的传输速率，结果显示，相同子网络、报文长度相同情况下本文方法传输报文的速率更快，说明经过本文方法优化调度之后，船舶网络具有较高报文传输效率，提升各个子网络的工作效率，降低报文传输的时延，具有较为良好的优化调度效果。

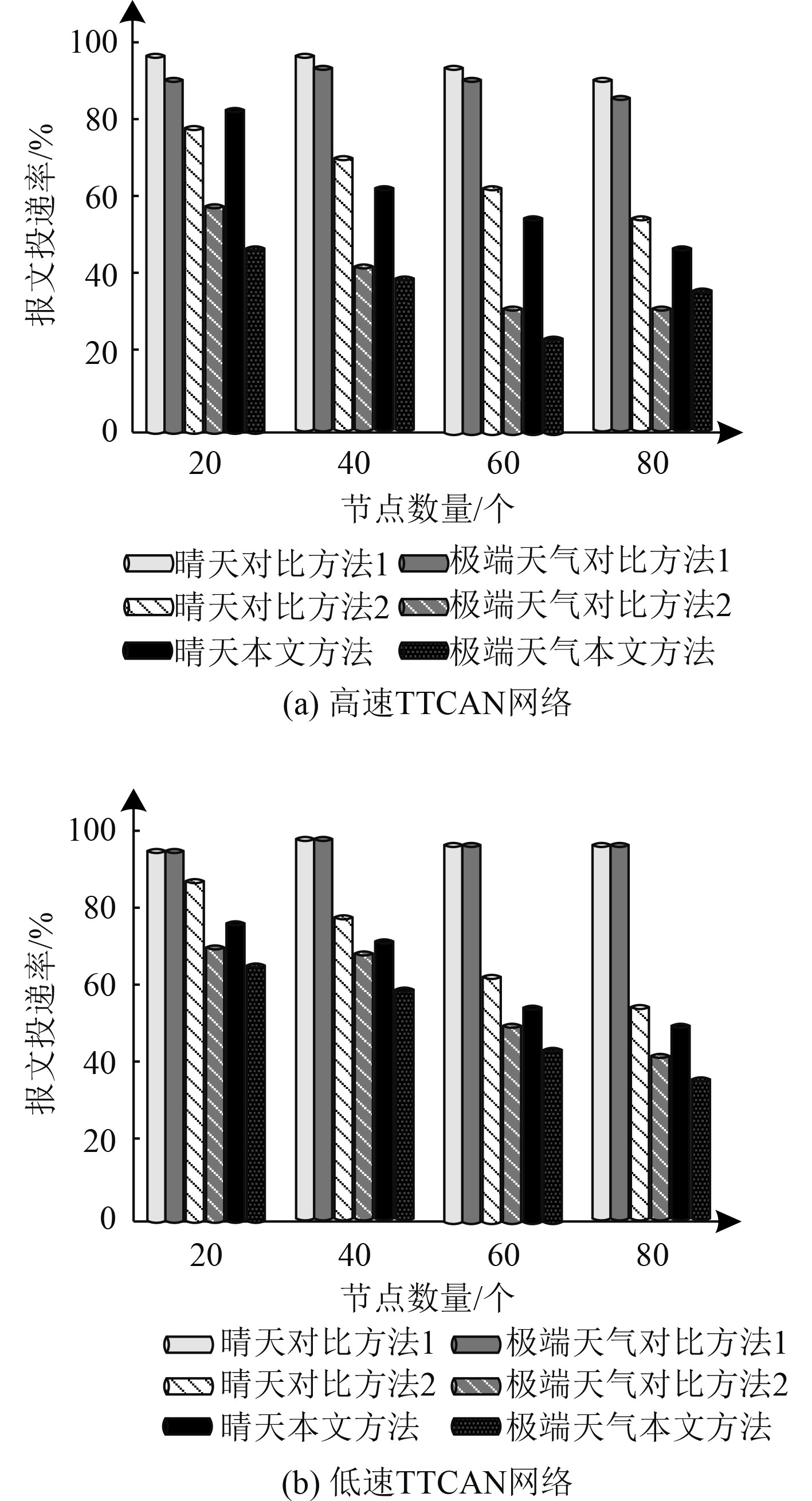
船舶航行过程中会遭遇各种不同天气，晴朗天气环境下，船舶正常运行，控制网络中的各个子网络都按照常规规定运行，报文传输较为规律，但是船舶航行也经常会遭遇极端天气，这种情况下，船舶控制的各个子网络就需要不停改变操作内容，多次更改指令，船舶网络的工作量加大，报文传输的投递率也出现显著变化。对比不同天气状况下，船舶航行时，不同TTCAN网络协议中，经不同方法优化调度后，网络传输报文的投递率，结果见图3。从图3（a）能够看出，高速TTCAN网络之中，对于报文传输的时效性要求较高，但是受到恶劣天气条件影响，船舶控制网络需要频繁更换运行指令，导致本文方法的报文投递率与晴天环境下的报文投递率相比略低，但是整体来看，使用本文方法优化调度后，报文投递率明显高于两种对比方法，证明本文方法的调度效果更优。低速TTCAN网络之中对于报文传输的时效性要求较低，报文传输有一个缓冲时间，所以即使网络节点数量增加，在不同天气环境下，使用本文方法优化调度网络之后，仍然能够保持较高的报文传输投递率。尽管与高速TTCAN网络相比，低速TTCAN网络之中对比方法优化调度之后，随着节点数量增加，报文传输投递率的下降幅度更小，但是与本文方法相比仍然不具备优势。综合来看，使用本文方法优化调度船舶网络之后，无论何种航行条件，仍然能够保证船舶的稳定航行。

3 结　语

船舶航行的环境复杂多变，网络传输的性能决定船舶的航行稳定性，本文研究改进遗传算法的船舶网络优化调度方法，将遗传算法与模拟退火算法相结合，以传输报文抖动最小作为优化调度的目标，同时改进遗传算法，计算得出最优解，获得船舶网络较为良好的优化调度效果。通过模拟试验发现，使用本文方法能够实现网络节点传输路径最短，同时使用本文方法只需要很短的时间就能实现各类船舶子控制系统的报文传输，优化调度效率较高；即使在较为复杂的天气条件之下，使用本文方法仍然能够保证报文在网络中的稳定传输，由此证明，经过本文方法优化调度的船舶网络具有较为良好的性能。