0 引　言

船舶通信系统整体包含3大类别，分别为视觉通信、声波通信以及无线电通信。由于船舶在航行过程中^[1]，海上气候和环境多变、复杂，对于通信存在一定影响，直接影响船舶的航行安全。因此，为了保证船舶内部通信信号的稳定^[2]、可靠传输，同时，避免通信线路铺设烦琐，降低建立成本，船舶载波通信系统成为船舶通信中重点研究的通信方式^[3]。船舶载波通信虽然具备上述优势，但是同时，其也存在一定缺点，例如其信号衰减较快等。因此，需对载波实行调制，保证通信精度的同时，解决信号衰减问题，并提升通信的抗干扰性能。多载波调制技术是用于数个载波的调制技术，其是通过对数据流实行分解，形成数个子数据流^[4]。常用的多载波调制技术有正交多载波调制(OFDM)、编码MCM(Coded MCM)等。

为实现船舶载波通信系统的载波调制，文献[5-6]分别对此展开研究，各自提出基于施密特正交化、基于广义信号索引的多载波调制方法，但是上述方法调制后，海况等级较高时，通信时信道的响应情况仍需进一步验证。因此，本文研究多载波调制技术在船舶载波通信系统中的应用方法，根据船舶载波通信信道特性，自适应确定调制的方式、频带以及比特功率的分配，使宽带的利用率最大化，完成多数据率传输，实现在不同距离、信道环境下通信。

1 船舶载波通信系统的自适应多载波调制 1.1 自适应多制式正交多载波船舶通信

任一OFDM码元之中均存在多个信号，且该信号为调制后子载波合成^[7]，该调制采用正交幅度调制(QAM)技术完成，发送信号的计算公式为：

$ x\left( t \right) = \sum\limits_{n = 0}^{N - 1} {d\left( n \right){e^{j2\pi {f_n}t}}}，\quad t \in \left[ {0,{T_s}} \right]。$

(1)

式中：第 $ n $ 个调制码元用 $ d\left( n \right) $ 表示，该值随着调制方式的改变而不同；时间间隔用 $ {T_s} $ 表示； $ {f_n} $ 表示路径的传播时延。在忽略保护时间的情况下，式(1)可简写为：

$ x\left( t \right) = X\left( t \right) \times \exp \left( {j2\text{π} {f_0}t} \right) $

(2)

式中： $ X\left( t \right) $ 表示船舶通信的基带信号，以速率 $ {f_s} $ 对其实行抽样处理。

$ d\left( n \right) $ 的反傅里叶变换(IDFT)用 $ X\left( k \right) = X\left( {{t_k}} \right) $ 表示，计算公式为：

$ X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {d\left( n \right)\exp \left( {j\frac{{2\pi }}{N}nk} \right)}。$

(3)

式中： $ 0 \leqslant k \leqslant \left( {N - 1} \right) $ 。

原始数据符号恢复时，接收端采用逆变换对 $ X\left( k \right) $ 实行处理，即可得出下述公式：

$ d\left( n \right) = \sum\limits_{k = 0}^{N - 1} {X\left( k \right)\exp \left( { - j\frac{{2\pi }}{N}nk} \right)}，$

(4)

多进制频移键控码元则可看作OFDM的特殊情况， $ d\left( n \right) $ 需满足下式：

$ d\left(n\right)=\left\{\begin{array}{*{20}{l}}1\text{，}&n=j\left(j=0,1,\cdots ,N-1\right)，\\ 0\text{，}&{\rm{others}}。\end{array}\right. $

(5)

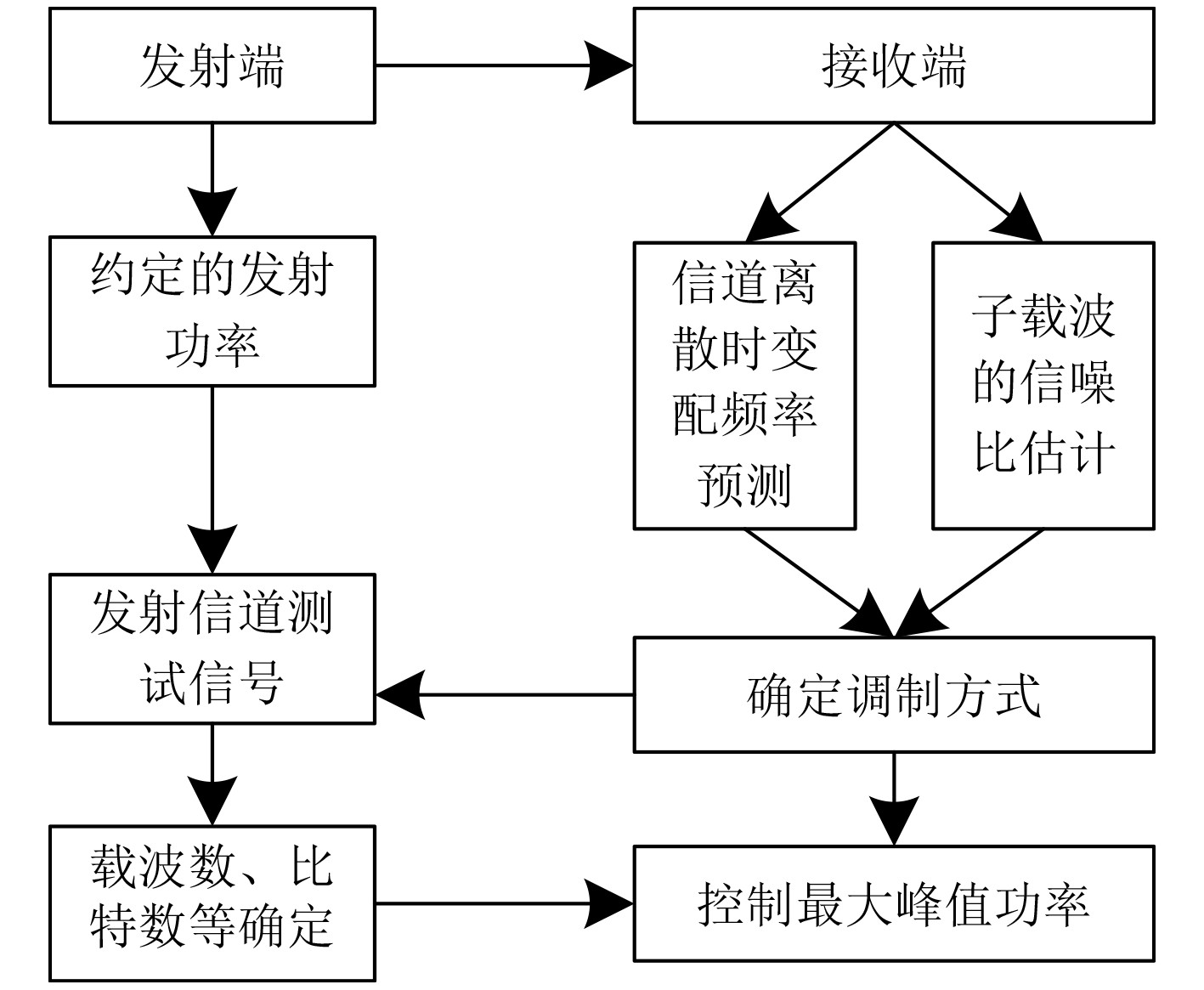
基于上述分析可知，自适应多制式正交多载波(MOMC)技术结合了多进制频移键控(MFSK)和OFDM两种技术组成，结合IDFT和傅里叶变换(DFT)完成船舶通信系统的调制和解调，无需其他操作；同时可以信道的预测结果为依据^[8]，基于奇异值低复杂度MOMC-OFDM系统自适应调制算法，自适应地选择调制方式以及分配对应的发送功率^[9]，完成船舶载波通信系统的多载波调制，整个调制流程用图1描述。整个流程中，以约定的发射功率为依据，由发射端发射信道测试信号，接收端收到该信号后，对当前的信道离散时变配频率结果实行预测，同时完成不同子载波的信噪比估计^[10]，以此确定此次的调制方式和船舶载波通信系统的工作频带。在此基础上，通过基于奇异值低复杂度MOMC-OFDM系统自适应调制算法确定调制方式的载波数、比特数等实行确定。发射、接收两端，依据该确定结果完成调制和解调，通过正交变换模式和调制编码结合方法，控制最大峰值功率，实现通信的稳定传输。

1.2 船舶载波通信系统载波比特、功率分配

基于自适应多制式正交多载波调制过程中，OFDM的子载波数量较多，且收发天线的数量较多，并且每一个收发天线之间的信道均相互独立，且具有相同的多径延迟分布。因此，船舶载波通信系统在通信时，每一帧数据的信道功率和比特分配结果几乎没有明显差距；在不同的信道状态下，信道的增益存在差异性，同时会导致子信道的功率和比特分配结果发生变化。本文采用基于奇异值低复杂度MOMC通信系统自适应调制算法，实现船舶载波通信系统载波比特、功率分配。

在分配过程中，该算法以第一帧数据为基础，依据信道功率增益，将该数据的奇异值子信道实行排列，排列顺序为由大到小，采用划分方式对排列后的子信道进行处理，保证将所有的子信道均划分至频域组内，且为均匀状态；各个频域分组均可通过一个子信道表示，且为等效。各个频域分组内的子信道和等效子信道的比特数和功率分配结果一致。按照上述内容完成分配后，保存并存储分配结果。其他帧的数据均依据该方案完成分配，以此即可完成船舶载波通信的多载波调制。

1.3 船舶载波通信系统的传输方案

完成船舶载波通信系统的多载波调制后，为保证最佳的通信效果，在进行信道分配功率时，需考虑峰值平均功率比对其的影响。因此，需对信道发送功率实行控制，保证信道功率在分配过程中，发射信号的峰值功率均位于射频功放工作范围内。采用正交变换模式和调制编码结合方法，完成最大峰值功率限制，实现船舶载波通信稳定传输，其步骤如下：

步骤1　求解峰均比因素的有效信噪比结果，以第 $ n $ 帧数据为基础，在其子载波信道频率响应计算结果的基础上完成，并属于接收端。

设 $ F $ ， $ I $ 表示2种正交变换模式，船舶载波通信确定的MFSK的 $ p $ 种调制编码方式为 $ {M_{F - p}} $ ，OFDM的 $ q $ 种调制编码方式为 $ {O_{I - p}} $ ，两者得到发射功率退回因子用 $ {\alpha _{F - p}} $ ， $ {\alpha _{I - q}} $ 表示，其公式为：

$ \left\{ {\begin{array}{*{20}{c}} {{\alpha _{F - p}} = {{10}^{\left( {c{m_R} - c{m_{F - p}}} \right)/10}}}，\\ {{\alpha _{I - q}} = {{10}^{\left( {c{m_R} - c{m_{I - q}}} \right)/10}}} 。\end{array}} \right. $

(6)

式中： $ c{m_R} $ 表示三次方度量参考值； $ c{m_{F - p}} $ 和 $ c{m_{I - q}} $ 分别表示三次方度量。

采用枚举方式计算 $ {M_{F - p}} $ 和 $ {O_{I - p}} $ 的信噪比，同时计算两者中的第 $ i $ 个子载波的信噪比，计算公式分别为：

$ \left\{ {\begin{array}{*{20}{c}} {{\varphi _{F - p - i}} = {{{\alpha _{F - p}}{{\left| {{H_i}} \right|}^2}} \mathord{\left/ {\vphantom {{{\alpha _{F - p}}{{\left| {{H_i}} \right|}^2}} {{\sigma ^2}}}} \right. } {{\sigma ^2}}}}，\\ {{\varphi _{I - p - i}} = {{{\alpha _{I - q}}{{\left| {{H_i}} \right|}^2}} \mathord{\left/ {\vphantom {{{\alpha _{I - q}}{{\left| {{H_i}} \right|}^2}} {{\sigma ^2}}}} \right. } {{\sigma ^2}}}} ，\end{array}} \right. $

(7)

$ \left\{ {\begin{array}{*{20}{c}} {\varphi _{I - p - i}^{comb} = \displaystyle\sum\limits_{j = 0}^{{N_{ant}} - 1} {\frac{{{\alpha _{F - p}}{{\left| {{H_{i,j}}} \right|}^2}}}{{{\sigma ^2}}}} }，\\ {\varphi _{I - q - i}^{comb} = \displaystyle\sum\limits_{j = 0}^{{N_{ant}} - 1} {\frac{{{\alpha _{I - q}}{{\left| {{H_{i,j}}} \right|}^2}}}{{{\sigma ^2}}}} } 。\end{array}} \right. $

(8)

式中： $ {H_{i,j}} $ 表示信道频率响应； $ {\sigma ^2} $ 表示噪声功率； $ {N_{ant}} $ 表示子载波数量。

依据式(10)和式(11)的计算结果，即可计算出2种编码方式下，各个子带的有效信干燥比结果 $ {\phi _{F - p}} $ 。

步骤2　依据步骤1计算结果，获取在充分结合最大功率限制的情况下，满足 $ FER < {10^{ - 1}} $ 的调制编码组合方式，获取的调制编码组合方式集合为：

$ {M_F} = \left\{ \begin{gathered} {M_{F - p}}|{\varphi _{FE{R_{F - p}} = 0.1}} < {\phi _{F - p}}, \hfill \\ p \in \left\{ {0,1, \cdots ,{N_{MCS}} - 1} \right\} \hfill \\ \end{gathered} \right\} ，$

(9)

式中： $ {\varphi _{FE{R_{F - p}} = 0.1}} $ 表示信噪比，且误帧率为10⁻¹。

步骤3　调制编码组合在 $ F $ ， $ I $ 两种模式下，有效频谱效率的计算公式分别为：

$ {E_{F - GMC}} = \mathop {\arg \max }\limits_{{M_{F = k}}} \left[ {{\xi _{F - k}} \times \left( {1 - {\varepsilon _{F - k}}} \right)} \right]，$

(10)

$ {E_{I - GMC}} = \frac{1}{\xi } \times \mathop {\arg \max }\limits_{{M_{I = k}}} \sum\limits_{m = 0}^{\xi - 1} {\left[ {{\xi _{I - k - m}} \times \left( {1 - {\varepsilon _{I - k - m}}} \right)} \right]}。$

(11)

式中： $ {M_{F - p}} $ 和 $ {O_{I - p}} $ 均表示保留的调制编码方式集合，前者属于MFSK获取的集合，后者属于OFDM获取的集合； $ {M_{F - k}} $ 和 $ {M_{I - k - m}} $ 均表示承载的信息比特数， $ {\varepsilon _{F - k}} $ 和 $ {\varepsilon _{I - k - m}} $ 均表示误帧率。

通过上述步骤，即可完成船舶载波通信系统的最大峰值功率限制，提高通信系统的功放效率和系统整体频谱效率，保证通信的最优化折中效果。

2 测试分析

将本文方法用于某巡逻船的载波通信系统中，该船需对巡逻海域的整体情况实行监控，获取巡逻范围内，海面状况、其他船只航行状况等，并得到巡逻信号采集结果。

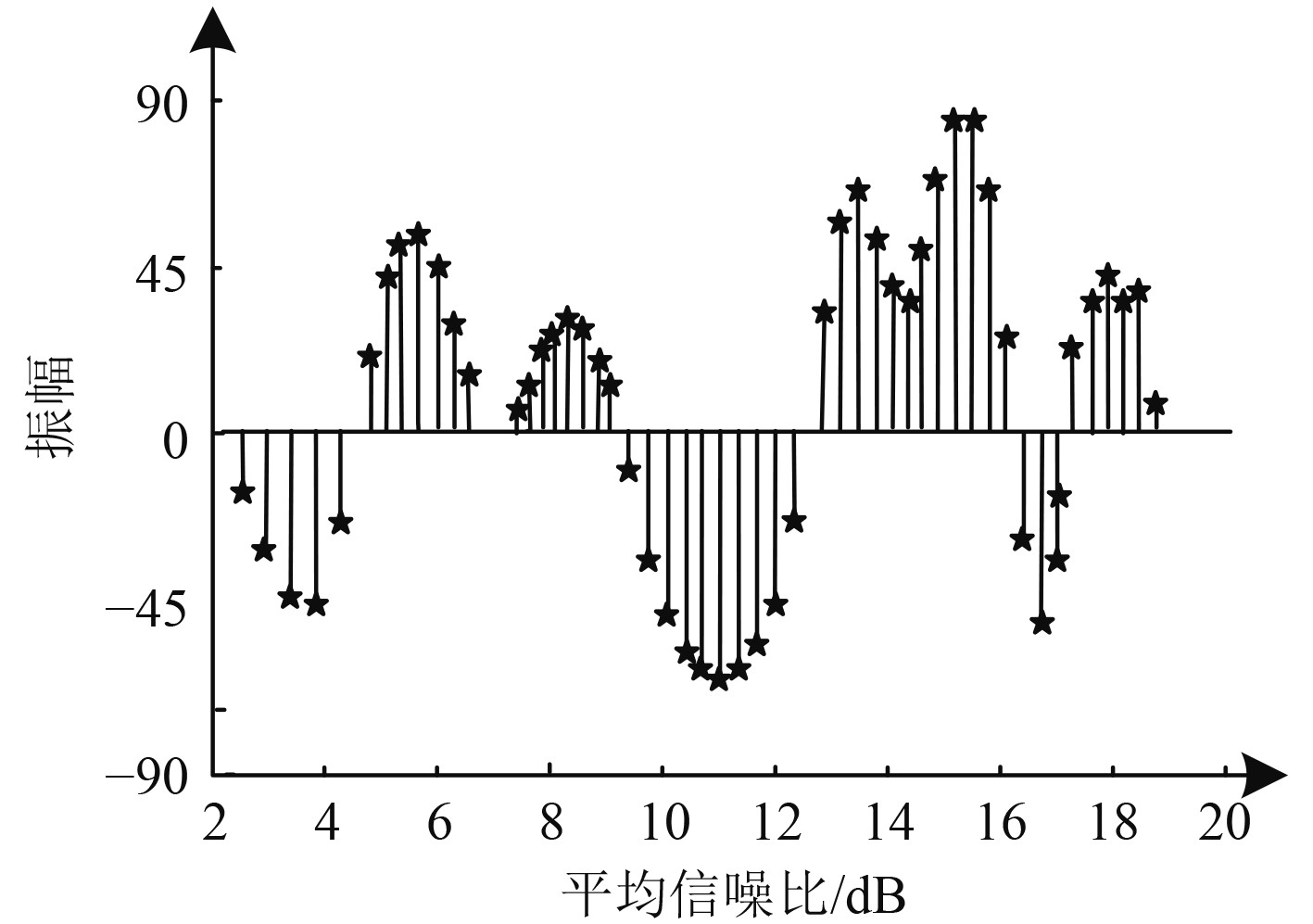
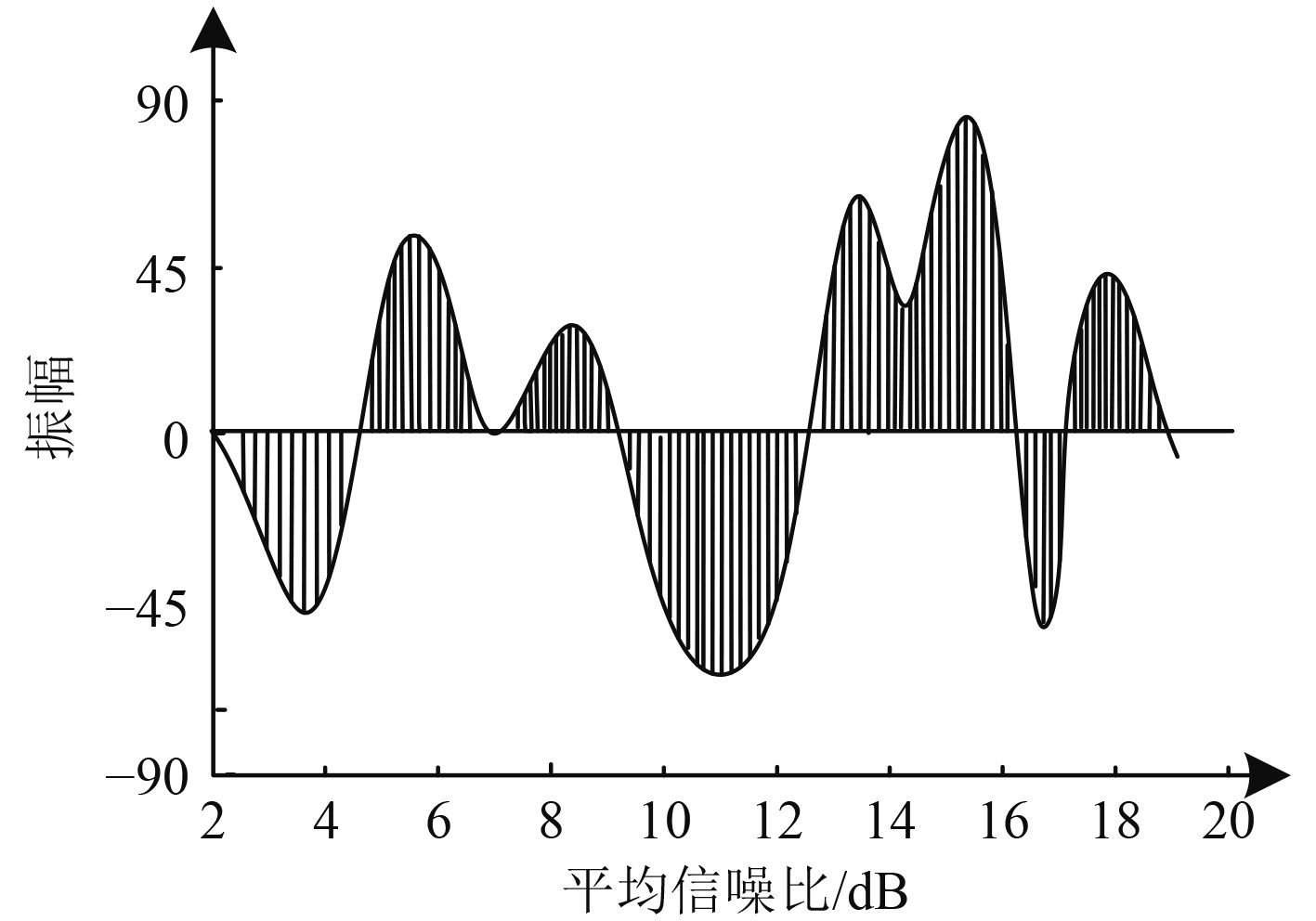
以巡逻采集的水下信号为例，对其实行调制，获取本文方法调制过程中，经过IDFT变换后输出时域信号的正交分量结果，用图2描述。在此基础上，在经过OFDM调制到发送的子载波上，形成待发送信号，发送端将该信号传送至接收端，接收端接收的信号结果用图3描述。对图2和图3测试结果进行分析后得出：本文方法具备良好信号调制性能，能够对信号实行调制，并生成待发送的信号频谱。调制后的信号发送后，接收端接收的同相、正交分量结果的波动与变换后的时域信号正交分量结果波动趋势吻合程度极高。因此，本文方法具备良好的信号调制性能，并且调制后的信号能够被完整、可靠接收。

船舶在巡逻时，会获取多种数据和信号，该测试仅选择最常用的声音、图像和文字等3种数据作为通信数据，进行传输，上述数据均属于低频信号，无法直接通过载波天线发送，需经过调制后进行传输。为测试本文方法的应用效果，以上述3种数据为例，获取本文方法在不同的通信距离下，3种数据在单位时间内多径分配比特率结果，用表1描述。其中比特率越高，表示单位时间内传送的数据量越大，通信性能越佳。对表1的测试结果分析后得出：随着距离的不断增加，3种数据在传输时，单位时间内多径分配比特率结果相对较为稳定，其变化波动范围在2.2～2.7 kbps之间，波动较小；即使距离较远的情况下，依然能够保证良好的比特率结果。这是由于本文方法在进行调制过程中，是以每个频域组为单位，全部子信道特征值序列排序结果为基础完成子信道的比特分配，因此，能够保证在远距离下，也可完成较大数据量的传输。

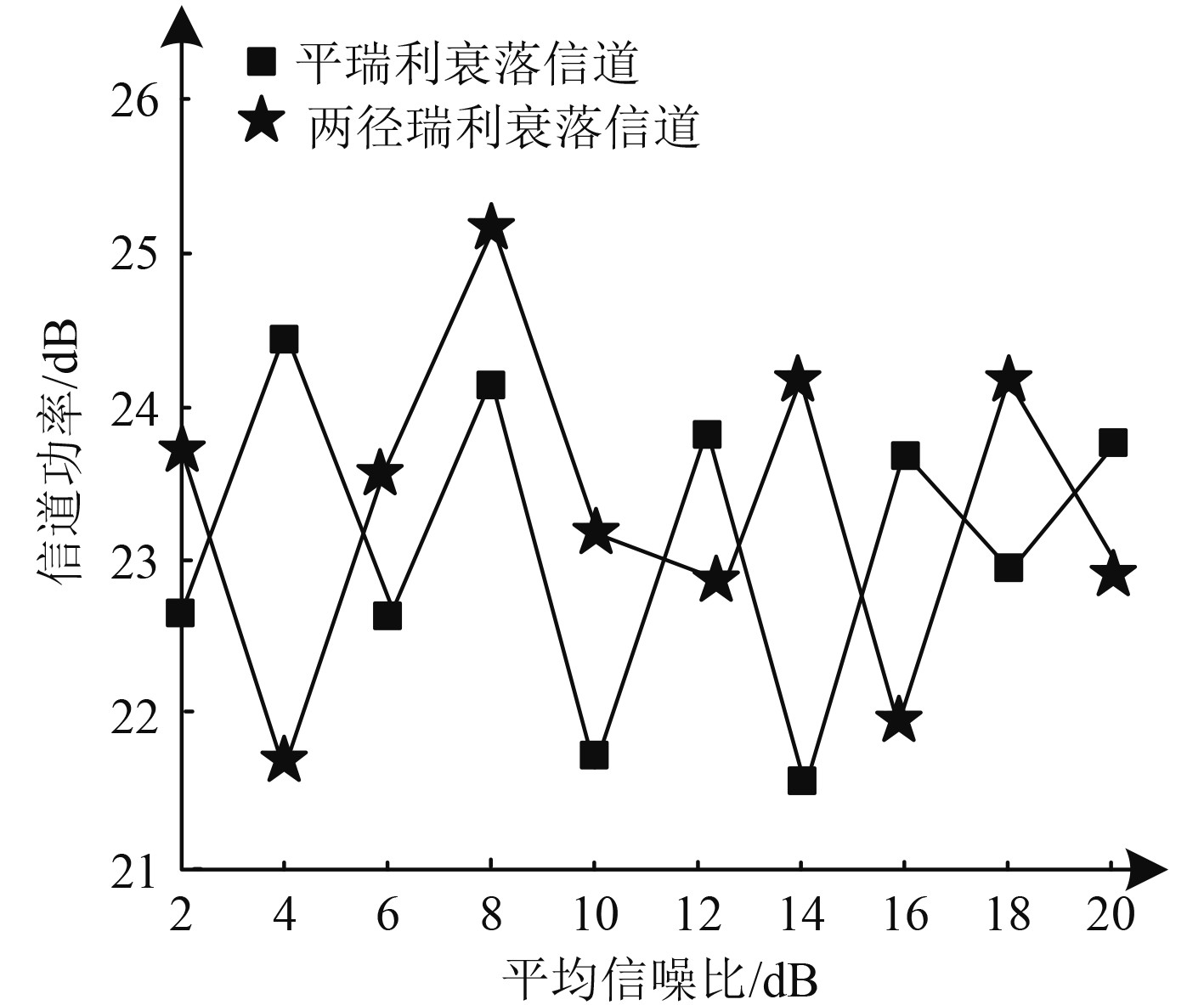
为进一步衡量本文方法的应用效果，以声音信号为例，将其在2种信道状态下进行数据通信，获取本文方法在2种信道状态下信道容量测试结果，用图4描述。对图4的测试结果分析后得出：在平瑞利衰落和两径瑞利衰落2种衰落信道状态下，随着平均信噪比的逐渐增加，本文方法调制后，信道容量结果均在21 bit以上，最高分别达到24.5 bit和25.2 kbps左右，满足应用需求。这是由于本文方法在调制过程中，依据MOMC-OFDM技术完成调制，实现信道功率分配，该技术能够完成衰落信道的转化，保证信道的平坦，提升信道容量。因此，调制后，能够保证良好的船舶载波通信效果。

3 结　语

载波通信系统是船舶之间采用的主要通信方式，该通信方式能够极大程度降低船舰之间的通信成本。但是为了提升该通信系统的信道容量，保证远距离的情况下依然能够较好完成通信，本文采用多载波调制技术对载波通信系统实行调制。测试结果显示，本文方法具备良好的多载波调制性能，调制后的信号不会发生损坏，能够完整进行通信，并且能够保证在远距离下，也可完成较大数据量的传输，通信的稳定性良好，满足应用需求。