2. 大连船舶重工集团有限公司,辽宁 大连 116005
2. Dalian Shipbuilding Industry, Co., Ltd., Dalian 116005, China
以燃气轮机为动力的水面舰船,受进气需求的影响,其船体表面外露了大量的进气格栅,格栅的雷达反射截面(RCS)的大小将影响舰船整体隐身水平。因此,开展船舶进气格栅隐身的设计与优化工作,使之具有良好的隐身性能,对提高水面舰船整体隐身水平十分有意义[1]。由于目标的RCS随几何外形和雷达波参数变化激烈,目前对目标几何外形进行雷达波隐身优化存在着计算时间消耗过大的问题。本文通过利用Kriging代理模型模拟进气格栅RCS与几何变量的变化关系,从而降低电磁散射的计算次数,提高、优化计算效率,实现对目标RCS的快速优化。
目前代理模型在航空气动性能、船舶水动力性能和结构性能等方面的优化计算中得到了广泛应用[2-4]。王刚成等[5]将Kriging代理模型引入船舶水动力性能多目标快速协同优化中,对船舶兴波阻力、垂荡和纵摇运动幅值进行了多目标快速优化,结果表明Kriging代理模型方法可以大幅提高船型优化效率。张晓东等[6]基于径向基神经网络和Kriging代理模型方法分别对水下垂直发射航行体、表面附着空泡闭合区压力预示模型进行了研究,结果表明在有限子样条件下,Kriging代理模型相对RBF方法对于空泡闭合区压力峰值预示精度更高。Qin采用Kriging模型和粒子群优化算法对混凝土连续铁路桥结构进行高阶模态识别,结果表明Kriging模型能较准确地预测分析响应,减少了计算时间[7]。
基于以上研究成果,为提高舰船设备雷达波隐身优化效率,本文以一典型舰船进气格栅为研究对象,利用Kriging代理模型模拟格栅RCS随几何变量的变化关系,并利用自适应遗传算法开展格栅在典型雷达波参数下的隐身性能优化,获得了进气格栅在该雷达参数下最优隐身方案。
1 Kriging代理模型优化方法代理模型的实现过程是利用已知的有限样本点数据构造一个与真实目标函数相近的数学模型。而通过对构造的数学模型进行优化计算,能够有效解决优化迭代过程中计算时长与计算精度之间的矛盾[8-9]。Kriging代理模型可以建立起n维输入
| $ {\hat y_l}\left( x \right) = F\left( {{\beta _{:,l}},x} \right) + {z_l}\left( x \right) \text{,} l = 1,\cdots,q,$ | (1) |
其中,F由p个经过挑选的函数
| $\begin{split} F\left( {{\beta _{:,l}},x} \right) = &{\beta _{1,l}}{f_1}\left( x \right) + \cdots+ {\beta _{p,l}}{f_p}\left( x \right) =\\ &\left[ {{f_1}\left( x \right),\cdots,{f_p}\left( x \right)} \right]{\beta _{:,l}} \triangleq f{\left( x \right)^2}{\beta _{:,l}},\end{split} $ | (2) |
式中,系数
| $ E\left[ {{z_l}\left( w \right){z_l}\left( x \right)} \right] = \sigma _l^2\tilde R\left( {\theta ,w,x} \right) \text{,} l = 1,\cdots ,q 。$ | (3) |
其中:
基于利用Kriging代理模型进行目标电磁散射特性仿真优化计算的框架如图1所示,其基本思路大致为:对每个参数在优化空间内进行试验抽样,调用进气格栅电磁散射特性计算初始样本获得精确的响应值,将响应值作为训练模型的最初样本集,建立初始代理模型;利用自适应遗传算法对代理模型进行最优解求解,获取当前预估得到的基于代理模型的全局最优解x*;计算x*的真实值,判断是否收敛。若x*真实值收敛,程序终止;若不收敛,则以x*为中心进行抽样以获得新样本点,计算新样本点的真实值。同时,将本次迭代生成新样本添加样本群中,构造新的代理模型。当不收敛时,通过自适应遗传算法不断迭代更新样本群和代理模型,直到最优解x*满足收敛条件。

|
图 1 雷达波隐身优化算法框架 Fig. 1 Radar wave stealth optimization algorithm framework |
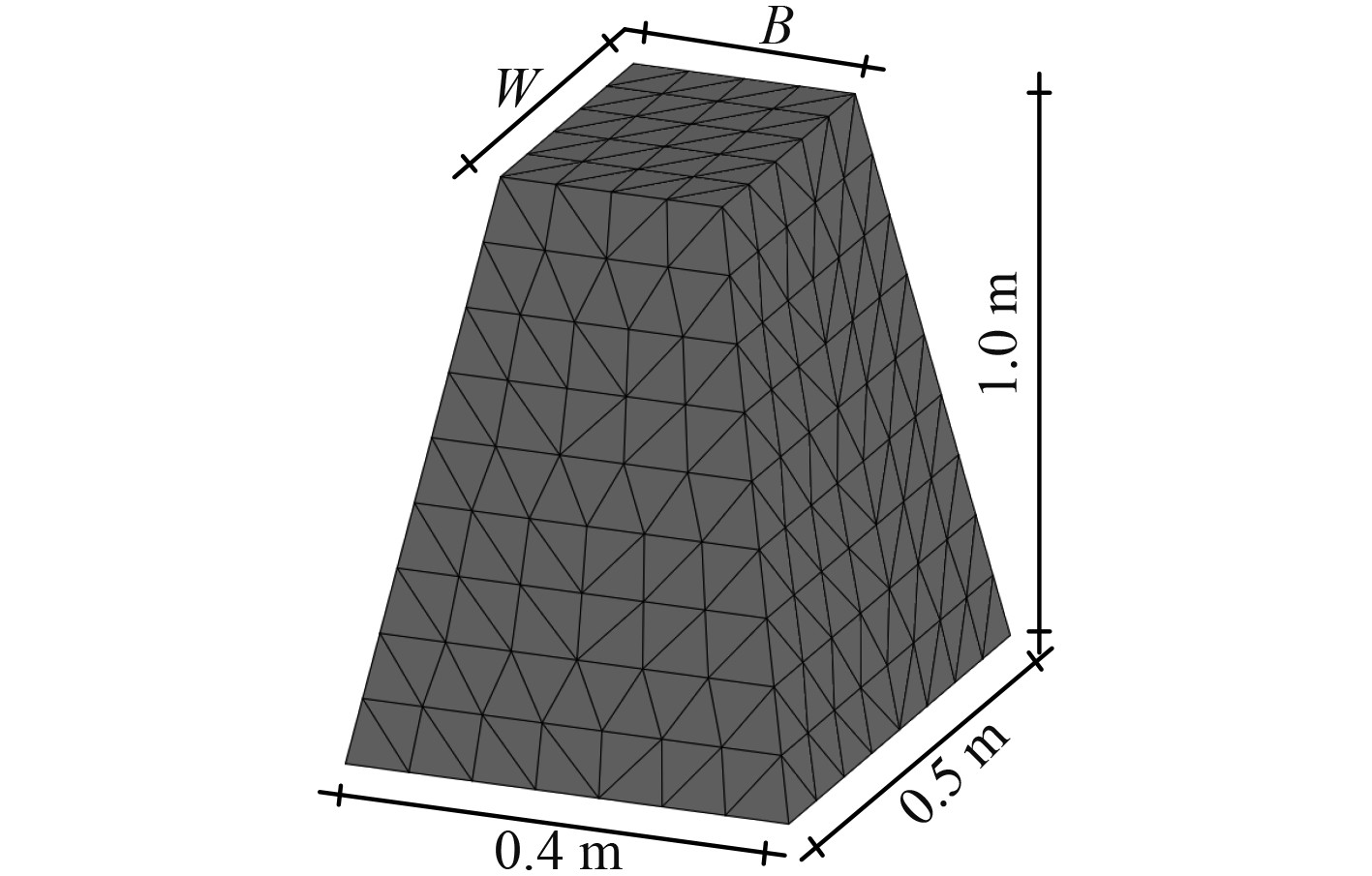
以一金属方台为目标,验证Kriging代理模型能否具备模拟目标几何变量与RCS平均值变化的能力,从而探究模拟目标RCS平均值随结合参数的变化规律。对仿真参数的设定如下:设雷达波入射电磁波波长为1 m,水平极化,角采样间隔为1°。
|
图 2 金属方台电磁散射模型 Fig. 2 Electromagnetic scattering model of metal cube |
通过仿真计算获得方台在水平角域上的RCS平均值随几何外形变量W和B的变化规律,如图3(a)所示。利用拉丁超立方LHS方法在实验域内随机抽样20个样本点,再通过Kriging代理模型方法对整个实验域内的RCS分布曲面进行模拟,最终模拟结果如图3(b)所示,图中散点代表采集的样本点。从图中结果可以看出Kriging模型能够较好地模拟了目标RCS平均值与外形几何变量W和B的变化特征。

|
图 3 RCS模型与拟合模型的比较 Fig. 3 Comparison of RCS function model and surrogate model |
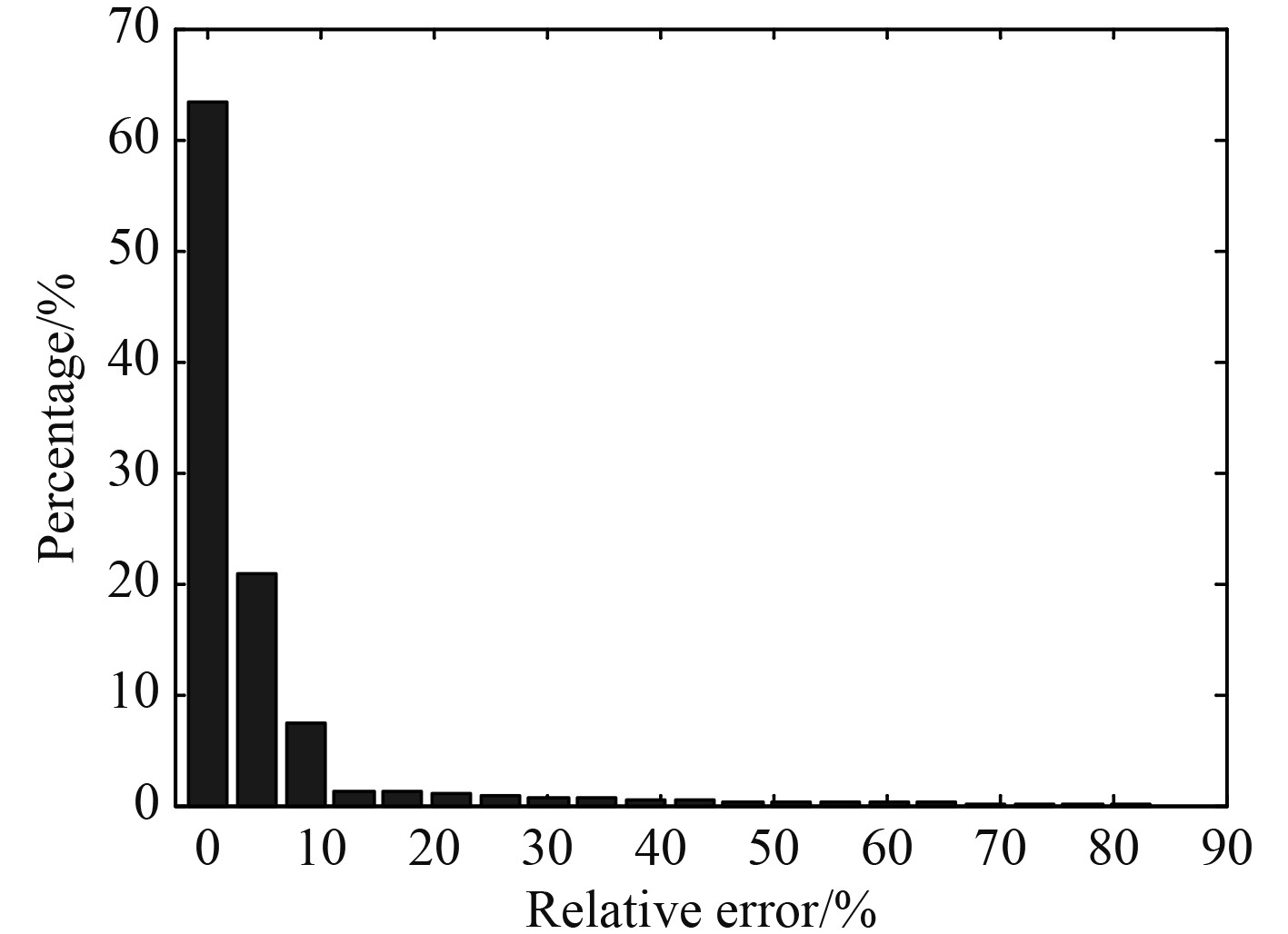
设定随机抽样数量为20,对图3(a)中的RCS分布曲面进行100次Kriging代理模型模拟,并统计计算整个实验域上各采样点的相对误差,结果如图4所示。仿真结果表明,整个试验域内相对误差的均值为4.50%,相对误差主要落在0~6%区间,且分布较为集中,由此可以看出Kriging代理模型在模拟金属方台RCS随几何参数变化规律时具有良好的计算精度。
|
图 4 代理模型相对误差分布 Fig. 4 Relative error distribution of the surrogate model |
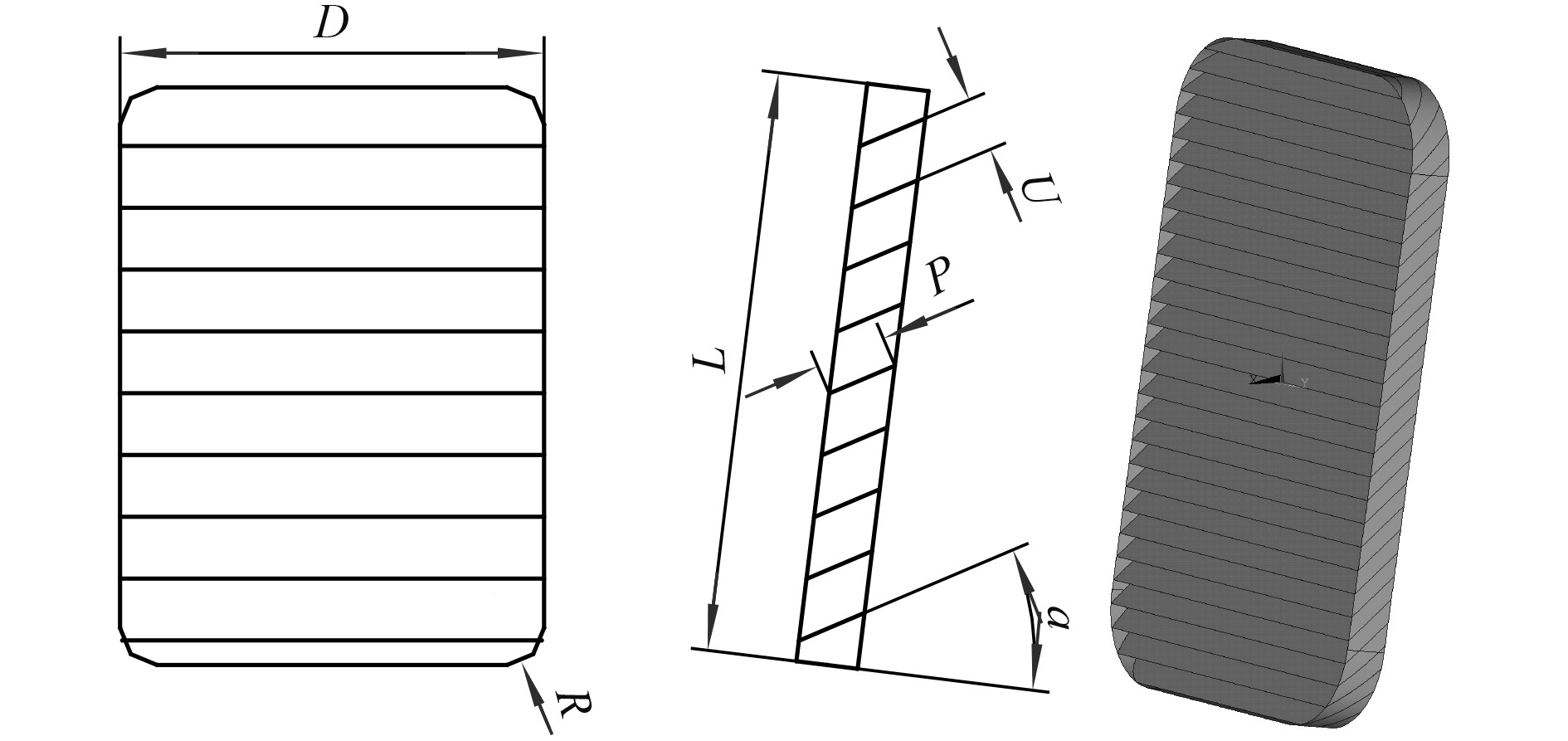
为实现对进气格栅隐身性优化分析,首先对进气格栅进行几何模型建模。对进气格栅的几何基本元素进行了分析和定义,参数具体定义及设定值如表1和图5所示。建模完成后,采用三角面元网格对模型进行划分,网格最大尺寸为1/8入射波长。设定进气格栅安装在斜角度为7°的船体外板,材料为理想金属。
|
|
表 1 进气格栅几何参数及初始值 Tab.1 Geometric parameters and initial values of air-intake grille |
|
图 5 进气格栅几何模型及参数定义 Fig. 5 Geometric model and geometric parameters of air-intake grille |
进行雷达波隐身优化时,仅针对沿水平威胁的雷达波展开,假定敌方入射波为3 GHz垂直极化雷达波,方位角φ的考评范围设定为−70°~70°,角采样间隔为1°。格栅整体尺寸远大于雷达波波长,叶片尺寸又不处于高频光学区,耦合散射和边缘散射不可忽略,故应用快速多极子方法[10]计算进气格栅的RCS。
综合考虑进气格栅装舰适用性和进排气约束,对进气格栅叶片宽度P、叶片间距U 、叶片与结构夹角α 这3个变量进行雷达波隐身优化,叶片宽度P范围设定为0.04 ~0.10 m,叶片间距U优化范围设定为0.015 ~0.06 m,叶片与结构夹角α 优化范围设定为40°~80°,并要求格栅安装后,水平方向的进气道完全被格栅叶片遮挡。格栅雷达波隐身优化目标函数设定为在评估区域内RCS平均值σavg,此时该桅杆雷达隐身外形优化数学模型可表述为:
| $ \left\{\begin{array}{l}{\rm{Find}}:P,U,\alpha ,\\ {\rm{Min}}:{\sigma }_{\text{avg}},\\ {\rm{s.t}}:\text{0.04m}\leqslant P\leqslant \text{0.10m},\\ \text{0.015m}\leqslant U\leqslant \text{0.06m},\\ {\text{40}}^{\text{o}}\leqslant \alpha \leqslant {\text{80}}^{\text{o}},\\ P\mathrm{sin}\alpha \text{cos(}\alpha -{7}^{\text{o}}) > U\mathrm{cos}{7}^{\text{o}}。\end{array}\right. $ | (4) |
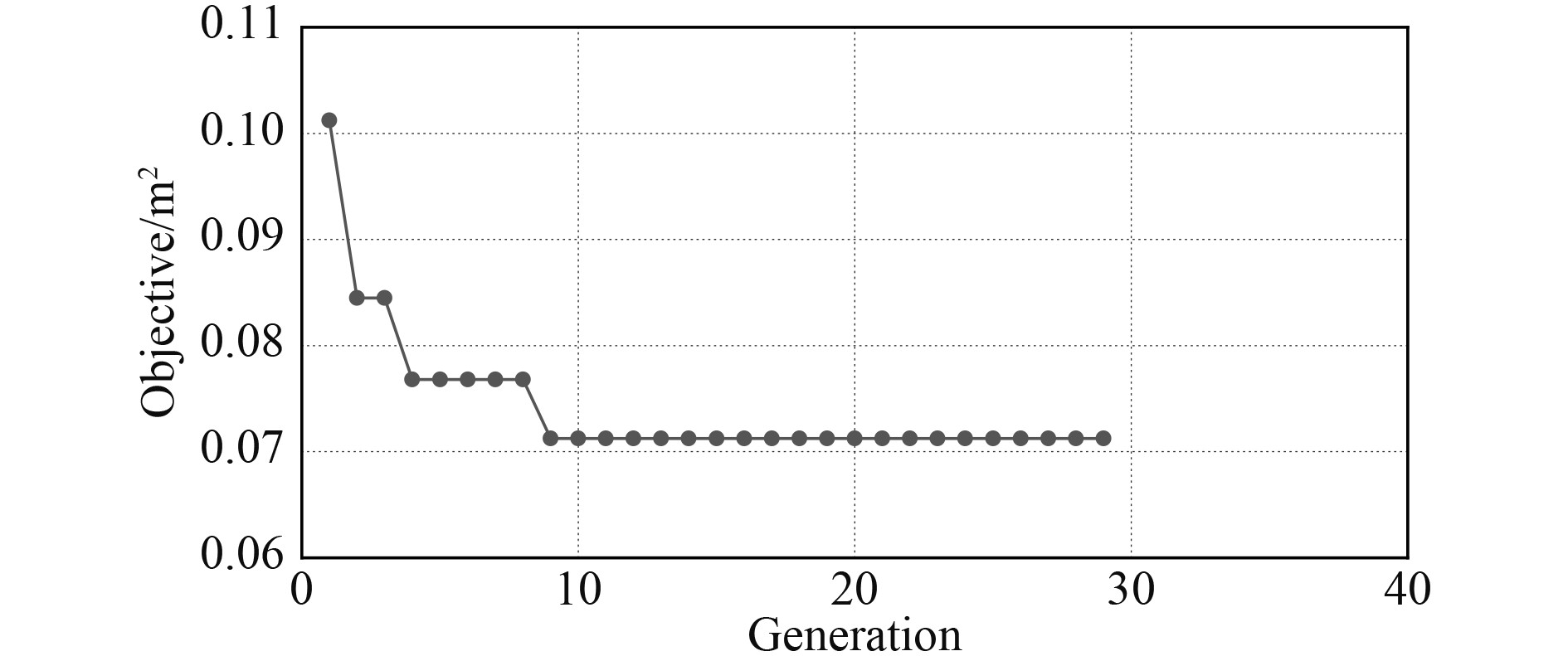
利用Kriging构建的优化算法对进气格栅开展RCS隐身优化计算,设定初始样本数量为30个,收敛条件设定为连续迭代20次最优解不变时终止,各次最优变量和最优结果如表2所示,具体迭代过程如图6所示。
|
|
表 2 雷达波隐身优化结果 Tab.2 Results of stealth optimization |
|
图 6 RCS优化迭代过程 Fig. 6 Iterative process of RCS optimization |
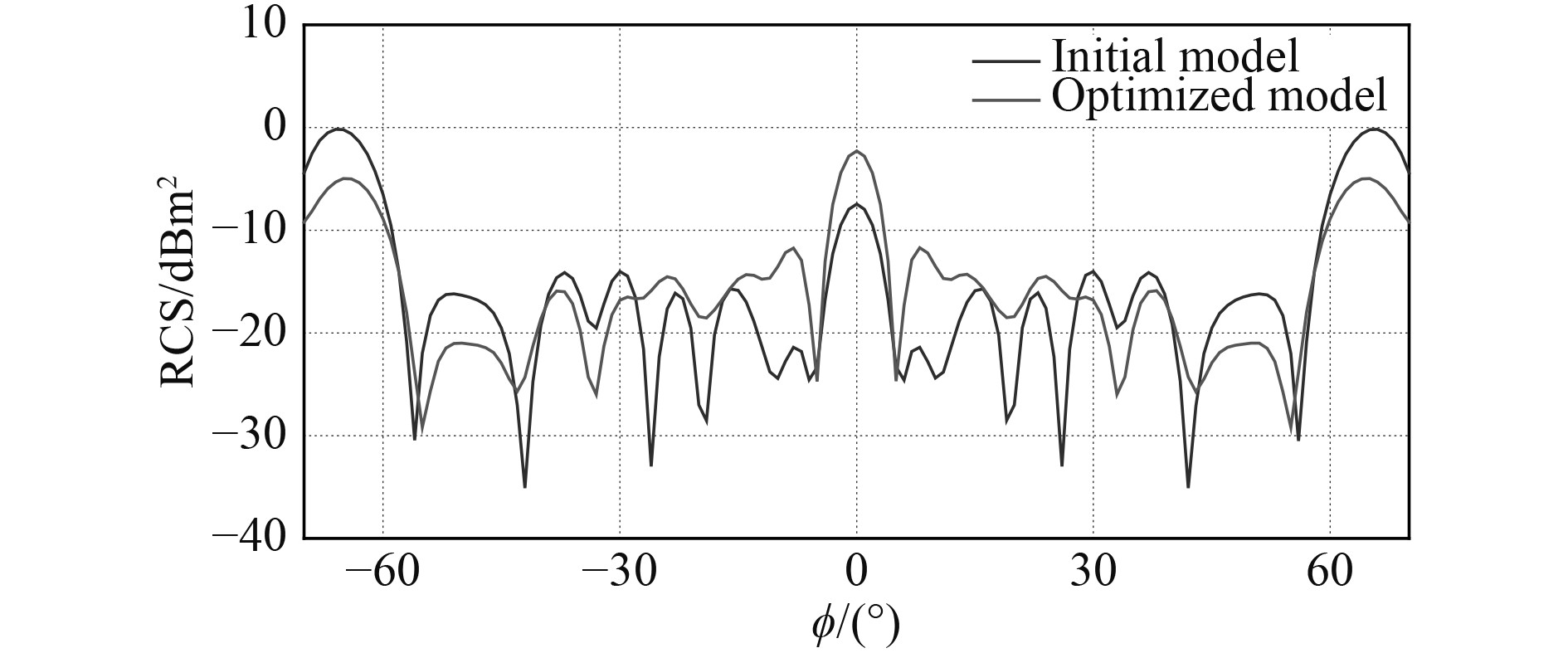
结果表明,经优化后,考评区域的RCS均值由0.123 m2降低至0.071 m2,在原来隐身设计方案的基础上降低约42%。优化前后的RCS分布结果对比如图7所示,优化后进气格栅在±65°处RCS主要峰值降低5.03 dB;除−28°~28°角度范围以外的RCS值绝大部分也有所降低。值得注意的是,优化后−28°~28°区域RCS有所变大,0°方向的RCS劣化5.2 dB,主要原因是σavg更容易受RCS峰值区域的影响,低RCS区域的变化对其的影响较小。
|
图 7 优化前后RCS分布对比 Fig. 7 RCS distribution after optimization |
为解决目标雷达波隐身优化计算消耗大的问题,提高舰船设备雷达波隐身优化效率,本文以典型舰船进气格栅隐身优化方案为研究对象,利用Kriging代理模型并结合自适应遗传算法对典型雷达波参数下格栅的隐身性能进行优化,得到结果如下:1)使用Kriging代理模型可以模拟金属方台目标RCS平均值随外形参数的变化规律,且具有良好的计算精度,整个试验域内相对误差的均值为4.50%;2)利用Kriging代理模型和自适应遗传算法对进气格栅隐身性能设计过程开展优化,获取了在典型雷达参数下进气格栅的最佳雷达隐身外形,其RCS均值在原隐身设计方案的基础上降低42%,隐身性有明显提升。本文使用的方法可以进一步利用在其他典型目标雷达波隐身设计过程中,优化其雷达波隐身计算效率。
| [1] |
杜晓佳, 丁凡. 舰船进气格栅隐身性分析及灵敏度计算[J]. 中国舰船研究, 2019, 14(6): 81-87. DU X j, DING F. Stealth analysis and sensitivity calculation of naval air-intake grille[J]. Chinese Journal of Ship Research, 2019, 14(6): 81-87. |
| [2] |
MUKHOPADHYAY T, CHAJRABORTY S, DEYS. A critical assessment of Kriging model variants for high-fidelity uncertainty quantification in dynamics of composite shells[J]. Archives of Computational Methods in Engineering, 2017, 24(3): 495-518. DOI:10.1007/s11831-016-9178-z |
| [3] |
JEONG S, MURAYAMA M, YAMAMOTO K. Efficient optimization design method using Kriging model[J]. Journal of Aircraft, 2005, 42(2): 413-420. DOI:10.2514/1.6386 |
| [4] |
罗文俊, 王德禹. 基于兴趣子域动态代理模型的船舶结构可靠性优化[J]. 中国舰船研究, 2021, 1-12. LUO W j, WANG D y. Reliability-based optimization of ship structure based on interest subdomain dynamic approximation model[J]. Chinese Journal of Ship Research, 2021, 1-12. |
| [5] |
王刚成, 马宁, 顾解忡. 基于Kriging代理模型的船舶水动力性能多目标快速协同优化[J]. 上海交通大学学报, 2018, 52(6): 666-673. WANG GC, MA N, GU X c. Fast collaborative multi-objective optimization for hydrodynamic based on Kriging surrogate model[J]. Journal of Shanghai Jiaotong University, 2018, 52(6): 666-673. |
| [6] |
张晓东, 权晓波, 王占莹. 代理模型在水下航行体空泡压力预示的应用研究[J]. 船舶力学, 2018, 22(1): 12-21. ZHANG X d, QUAN X b, WANG Z y. Research on the prediction method of unsteady cavity pressure development of underwater vehicle based on surrogate model[J]. Journal of Ship Mechanics, 2018, 22(1): 12-21. DOI:10.3969/j.issn.1007-7294.2018.01.002 |
| [7] |
QIN S, ZHANG Y, ZHOU Y L. Dynamic model updating for bridge structures using the Kriging model and pso algorithm ensemble with higher vibration modes[J]. Sensors, 2018, 18(6): 1879. DOI:10.3390/s18061879 |
| [8] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. |
| [9] |
宋磊, 王建, 杨卓懿. Kriging模型在潜器型线优化设计中的应用研究[J]. 船舶力学, 2013, 17(Z1): 8-13. SONG L, WANG J, YANG Z Y. Research on shape optimization design of submersible based on Kriging model[J]. Journal of Ship Mechanics, 2013, 17(Z1): 8-13. |
| [10] |
SONG J, CHE W W. Fast multipole method solution using parametric geometry[J]. Microw. opt. Technology. Lett, 2010, 7(16): 760-765. |
 2022, Vol. 44
2022, Vol. 44
