卫星助降系统是基于卫星导航的着舰引导系统,目前建成并投入运营的卫星导航系统主要有美国的GPS,俄罗斯的GLONASS,欧洲的Galileo和中国的北斗系统。北斗系统是我国具有完全自主知识产权的卫星导航系统,但其作为一种无线电被动定位系统,系统的服务性能不能保证100%,同时也有自身固有的缺陷,比如达到地面功率极低、易被干扰或者欺骗。在航空器起降等涉及生命财产安全领域,完好性监测是基于北斗的着舰引导系统迫切需要解决的关键问题之一[1]。
为了提高系统的可靠性,舰船中布设多个基准站接收机。多个基准站间观测进行相互比对,排除异常观测。多基准站处理一般基于构造一种观测数据的参考值B值。B值反映检测统计量与均值的差异,在没有卫星和参考接收机故障情况下,B值在一个稳定的范围内变化。一旦存在卫星或接收机故障,将导致B值的异常波动[2]。
应用于民航着陆的GBAS系统,多个卫星导航参考站部署于机场经过精确标定的不同固定位置,经过完好性检测后,播发差分校正消息。机载端接收差分校正信息,在定位模式上,采用伪距差分的方式,因此,GBAS系统主要进行伪距B值监测,B值定义为伪距修正量均值与排除了某个参考站之后的伪距修正量均值之差[3-4]。
着舰系统中,母舰位置上处于运动状态,受海浪影响,姿态上具有六自由度扰动,因此部署在母舰上的参考站不具有固定位置的约束条件,无法计算伪距修正值[5]。甲板跑道相比于机场跑道更为狭小,对于定位精度要求更高,需要采用基于载波差分的相对定位方法。因此,在完好性监测上更多的关注载波相位观测,需要对载波相位进行监测[6-8]。由于多接收机布局于舰船不同位置且在ECEF坐标系中相对位置随时变化,同时由于钟差和载波相位整周模糊度的存在,多基准站接收机产生的载波相位不能直接进行一致性比对[9-10]。为了建立站间载波观测的可比性关系,需要将参考站的载波相位观测虚拟到同一个舰船参考点上,并采取一定措施,消除钟差和整周模糊度的影响。
1 载波相位虚拟算法模型基于载波差分的着舰引导系统舰船上卫导布局参见图1,包括4个参考站,所布设的卫导天线分别为为GNSS天线A、GNSS天线B、GNSS天线C、GNSS天线D,Os为舰船参考点,Ts为理想着舰点。载波相位虚拟的目的是将多站载波相位观测值虚拟到同一个点P,本文中P点与Os点重合。

|
图 1 舰船多GNSS参考站布局示意图 Fig. 1 Multi GNSS station location in ship |
多站卫导接收机获取到编号
| $ \lambda \phi _n^i = r_n^i - I_n^i + T_n^i + c\delta {t_{rn}} - c\delta t_s^i + N_n^i\lambda + {\varepsilon _{{\phi _n}}}。$ |
其中:
B,C,D相对于A的站-星双差观测为:
| $ \lambda \nabla \Delta \phi _{AB}^{ij} = \nabla \Delta r_{AB}^{ij} - I_{AB}^{ij} + T_{AB}^{ij} + \lambda \nabla \Delta N_{AB}^{ij},$ |
| $ \lambda \nabla \Delta \phi _{AC}^{ij} = \nabla \Delta r_{AC}^{ij} - I_{AC}^{ij} + T_{AC}^{ij} + \lambda \nabla \Delta N_{AC}^{ij},$ |
| $ \lambda \nabla \Delta \phi _{AD}^{ij} = \nabla \Delta r_{AD}^{ij} - I_{AD}^{ij} + T_{AD}^{ij} + \lambda \nabla \Delta N_{AD}^{ij}。$ |
在GBAS系统中,基于已精确标定A,B,C,D站址坐标和广播星历,计算星站距离
| $ V_A^B = I_{AB}^{ij} - T_{AB}^{ij} = - \lambda \nabla \Delta \phi _{AB}^{ij} + \nabla \Delta r_{AB}^{ij} + \lambda \nabla \Delta N_{AB}^{ij} ,$ |
| $ V_A^C = I_{AC}^{ij} - T_{AC}^{ij} = - \lambda \nabla \Delta \phi _{AC}^{ij} + \nabla \Delta r_{AC}^{ij} + \lambda \nabla \Delta N_{AC}^{ij},$ |
| $ V_A^D = I_{AD}^{ij} - T_{AD}^{ij} = - \lambda \nabla \Delta \phi _{AD}^{ij} + \nabla \Delta r_{AD}^{ij} + \lambda \nabla \Delta N_{AD}^{ij}。$ |
假设虚拟站点为
| $ \lambda \nabla \Delta \phi _{AP}^{ij} = \nabla \Delta r_{AP}^{ij} - I_{AP}^{ij} + T_{AP}^{ij} + \lambda \nabla \Delta N_{AP}^{ij},$ |
| $ \lambda \left( {\Delta \phi _P^{ij} - \Delta \phi _A^{ij}} \right) = \nabla \Delta r_{AP}^{ij} - V_A^P + \lambda \nabla \Delta N_{AP}^{ij}。$ |
其中:
| $ V_A^P = T_{AP}^{ij} - I_{AP}^{ij} 。$ |
虚拟站点的单差观测为:
| $ \lambda \Delta \phi _P^{ij} = \lambda \Delta \phi _A^{ij} + \nabla \Delta r_{AP}^{ij} - V_A^P + \lambda \nabla \Delta N_{AP}^{ij} 。$ |
其中:
| $ \nabla \Delta r_{AP}^{ij} = \left( {r_A^i - r_A^j} \right) - \left( {r_P^i - r_P^j} \right) 。$ |
根据A点坐标和已测绘的相对位置基线,可以得到虚拟点P点的坐标,结合卫星星历数据,可以求解
| $ \lambda \Delta \phi _P^{ij} = \lambda \Delta \phi _P^i - \lambda \Delta \phi _P^j = \lambda \Delta \phi _A^i - \lambda \Delta \phi _A^j + \nabla \Delta r_{AP}^{ij} - V_A^P。$ |
参考星的电离层-对流层误差假设为0,参考卫星的虚拟非差观测值为:
| $ \lambda \phi _P^i = \lambda \phi _A^i + \Delta r_{AP}^i,$ |
非参考卫星的虚拟非差观测值为:
| $ \lambda \phi _P^j = \lambda \phi _A^j + \Delta r_{AP}^j - V_A^P 。$ |
A,B,C,D等参考站布局同一舰船上,相对之间距离在几百米以内,卫星信号传播到4个参考站经过的传输路径基本一致,因此电离层延迟、对流层延迟基本一致,即
| $ I_a^i = I_b^i = I_c^i = I_d^i\begin{array}{*{20}{c}} ,&{T_a^i = T_b^i = T_c^i = T_d^i} \end{array}。$ |
在超短基线中,可以假设
| $ \lambda \phi _P^i = \lambda \phi _A^i + \Delta r_{AP}^i。$ |
为了保证更好的观测质量和一致性结果,舰船多参考站接收机采用同一型号卫导天线和接收机,并通过公共的外部高精度时钟为接收机提供频率基准,因此,接收机噪声服从同分布,接收机钟差保持一致,即
| $ c\delta {t_{ra}} = c\delta {t_{rb}} = c\delta {t_{rc}} = c\delta {t_{rd}} 。$ |
基于卫星的着舰引导系统中,通过上述方式,将各参考站的测量载波相位从天线位置映射转换到同一个参考点
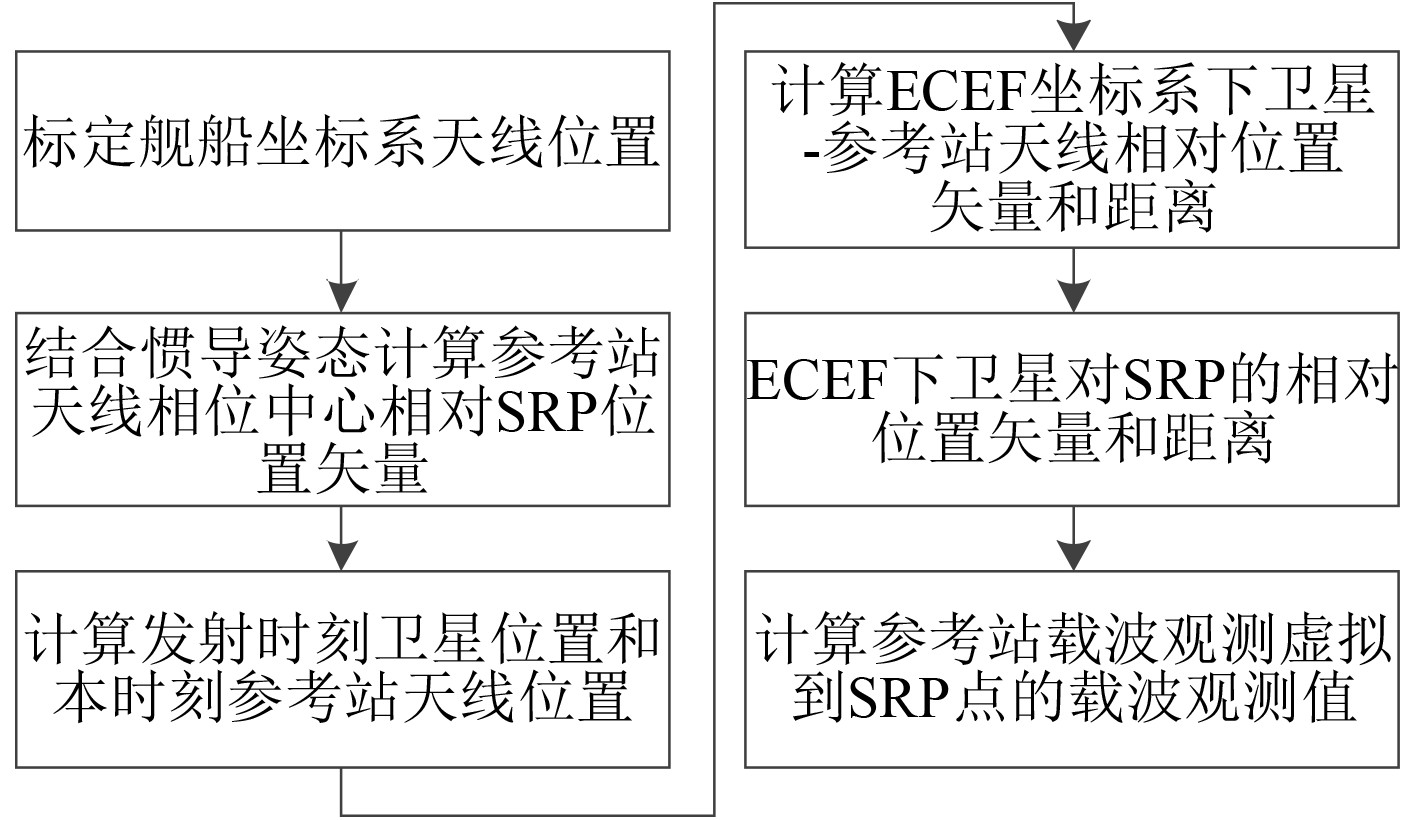
基于载波相位差分的着舰引导系统载波相位虚拟观测生成方法参见图2,其具体步骤如下:
|
图 2 着舰引导虚拟载波相位生成 Fig. 2 Virtual carrier phase generation for shipboard landing |
首先,精确标定在舰船坐标系中参考站天线相位中心相对于舰船参考点SRP的位置矢量
| $ {\vec R_0} = {\boldsymbol{C}}_b^e{\vec R_r}。$ |
其中:
根据广播星历和伪距计算信号发射时刻卫星的位置
| $ \vec R_1^i = \vec P_{}^i - \vec R_j^{} \text{,} d_1^i = \left\| {\vec R_1^i} \right\| 。$ |
计算ECEF坐标系下卫星相对于SRP的位置矢量
| $ \vec R_2^i = \vec P_{}^i - \vec R_j^{} + {\vec R_0} \text{,} d_2^i = \left\| {\vec R_2^i} \right\|。$ |
计算参考站本历元载波相位与卫星到参考距离
| $ {D_e} = {\phi ^i} - d_1^i 。$ |
计算参考站载波相位换算到SRP点处的虚拟载波相位观测值,即
| $ \phi _{vrs}^i = d_2^i + {D_e}。$ |
将第1次多个参考站均接收到编号
同理,伪距可以采用同类的方式获取虚拟伪距观测:
| $ \rho _{vrs}^i = d_2^i + {D_e}。$ |
舰船参考站间的载波和伪距观测虚拟影响因素为单点定位误差、卫星星历误差、测姿误差、参考站位置标定误差、含载体形变、电离层误差和对流层误差。其中,参考站位置标定误差利用高精度光学传感器可以达到毫米级别,载体形变则基于补偿技术限制其影响,电离层和对流层误差由于参考站间基线超短(几百米以内) ,因此可以忽略。讨论单点定位误差、卫星星历误差和惯导姿态误差的影响。
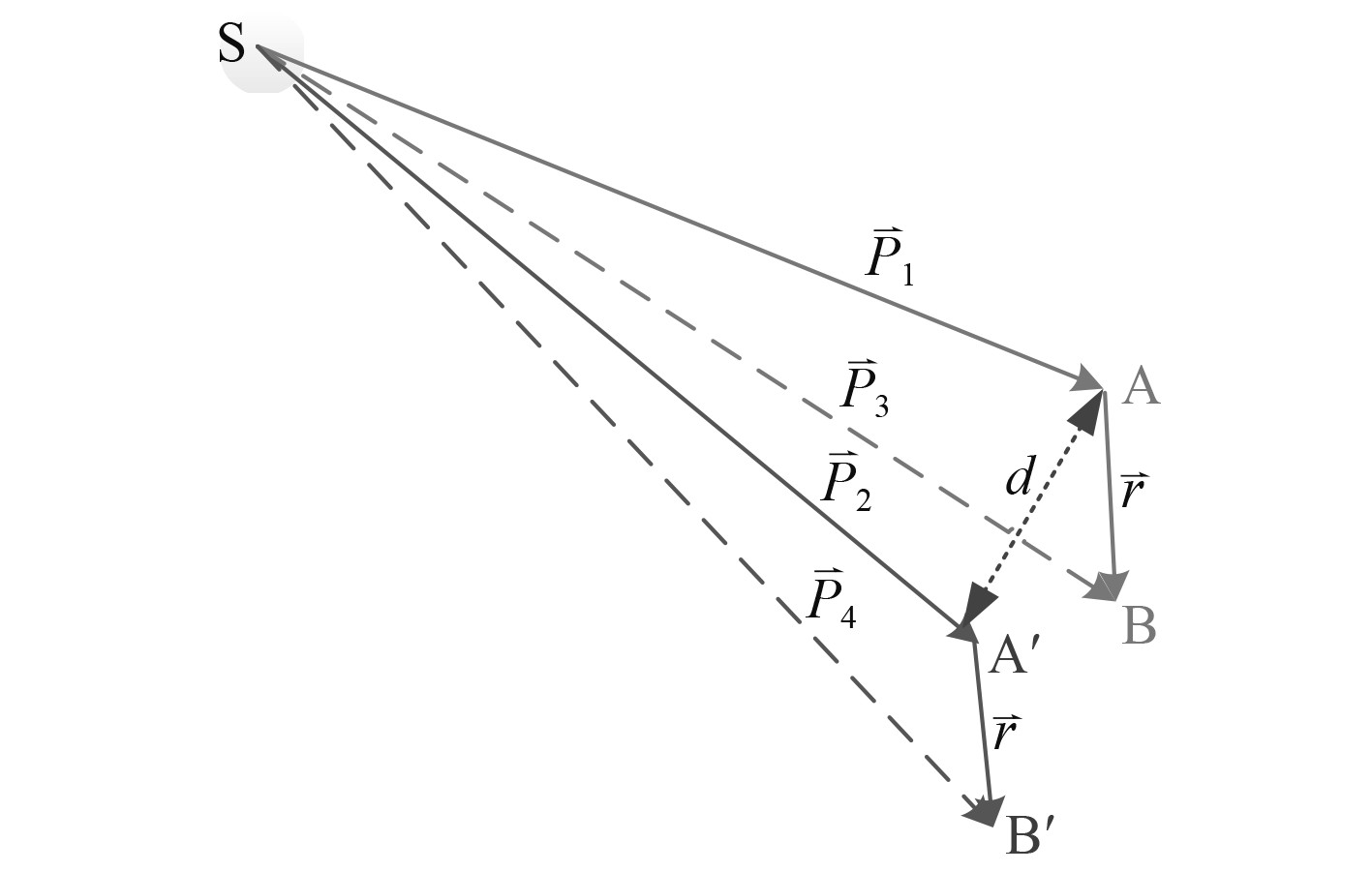
图3为卫星一观测站伪距与几何距离示意图。图中,S为卫星,A为用户实际位置,A'为用户计算自身位置。B为实际位置经过杆臂转换的位置,B'为户计算位置杆臂转换后的位置。
|
图 3 卫星-观测站伪距与几何距离示意图 Fig. 3 Pseudorange and geometry distance of satellite to user |
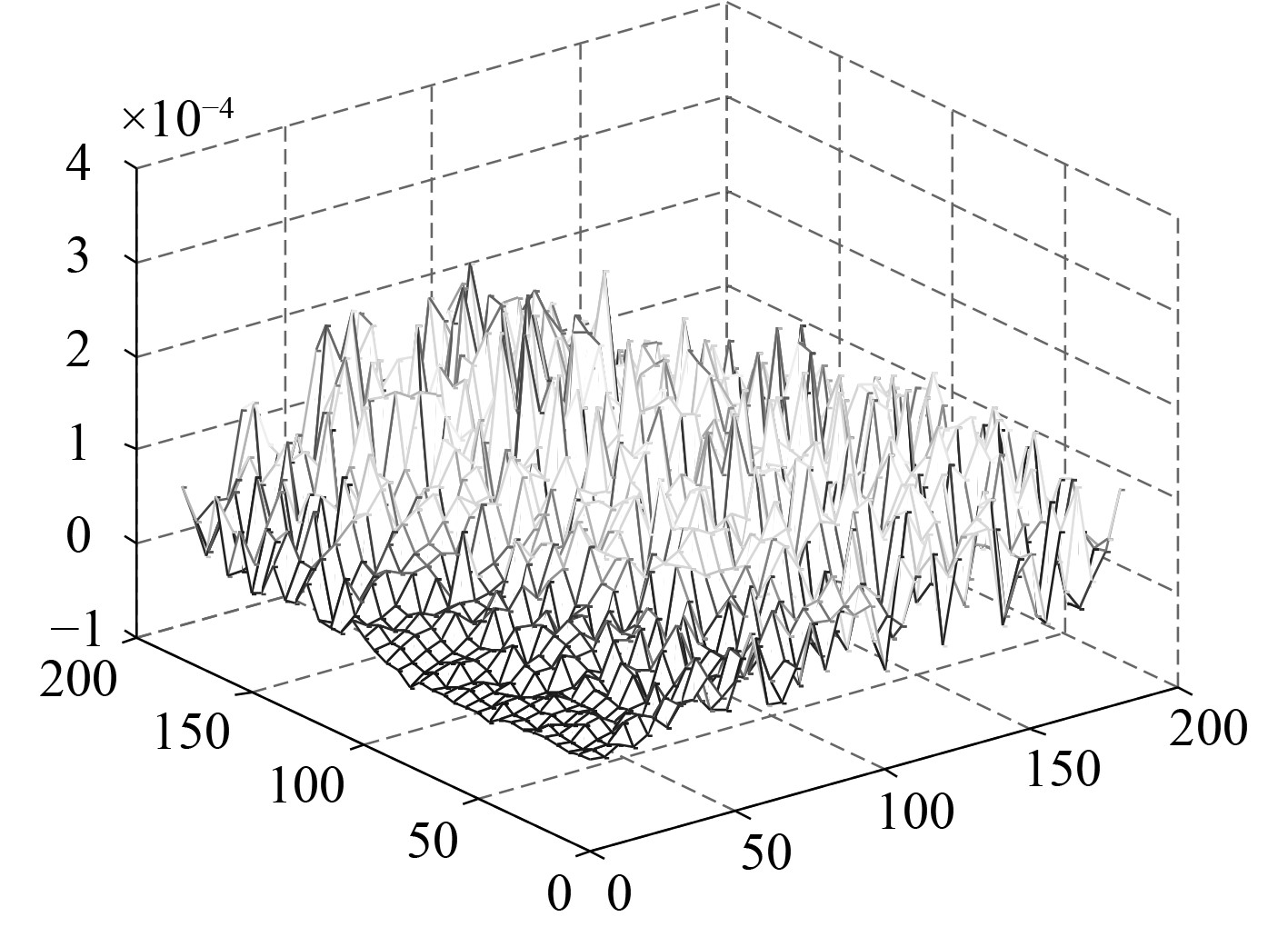
假设单点定位误差30 m,对不同仰角和方位角进行遍历仿真,从图4可以看出,单点定位误造成的距离测量偏差最大不超过0.3 mm。
|
图 4 单点定位对虚拟载波相位影响 Fig. 4 Effect of position precesion on virtual carrier phase |
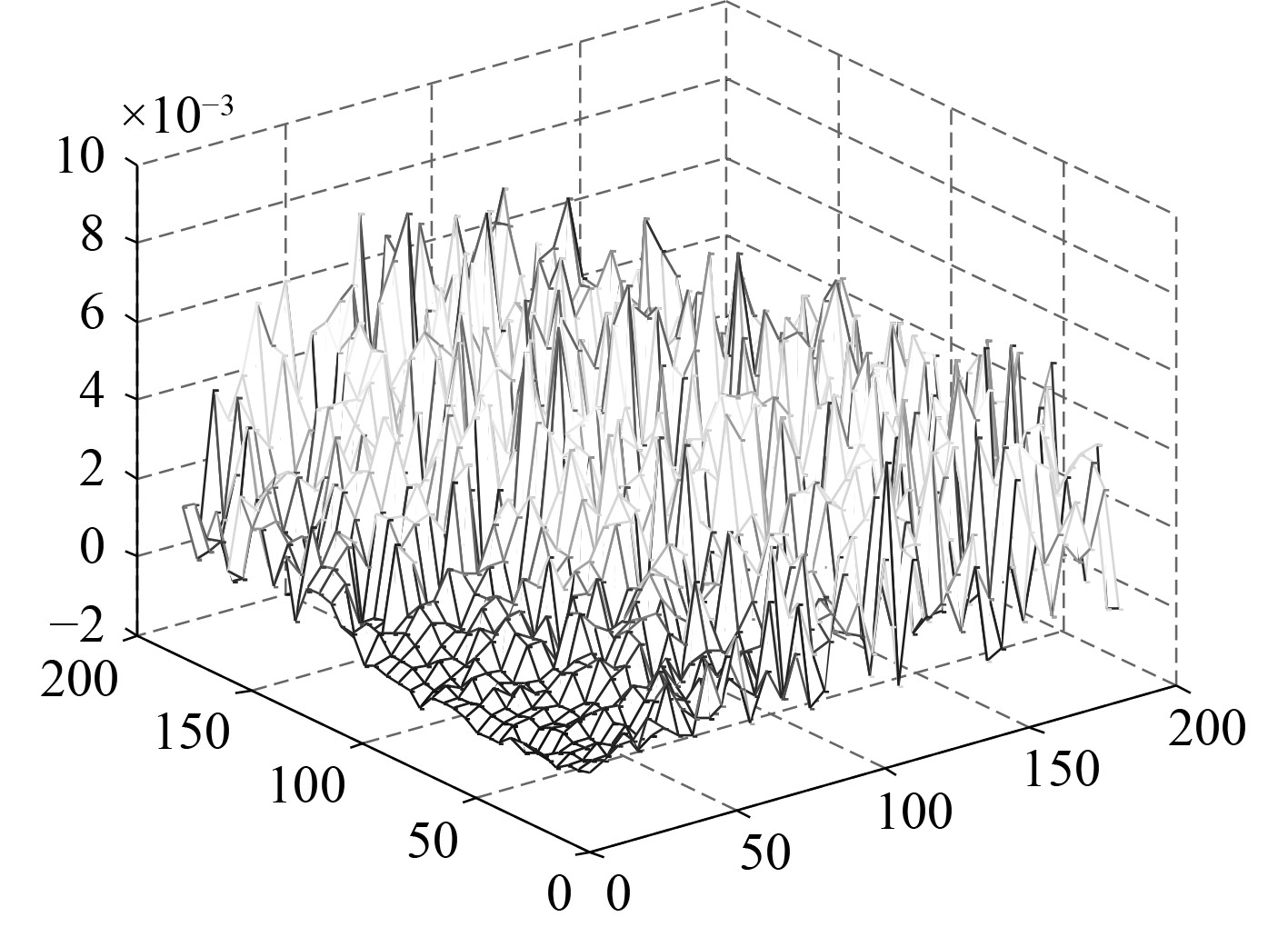
星历误差,整体加到单点定位误差上去,当星历误差为1 000 m时,对于测距影响最大不超过8 mm,同时差分计算时针对同一颗卫星进行了站间差,可以进一步降低星历误差影响(见图5)。
|
图 5 星历误差对虚拟载波相位影响 Fig. 5 Effect of ephemeris error on virtual carrier phase |
假设基于多天线测姿技术手段获取载体姿态,姿态测量误差0.005°,基线长度假设为173 m,造成的距离测量最大误差为28 mm(见图6)。
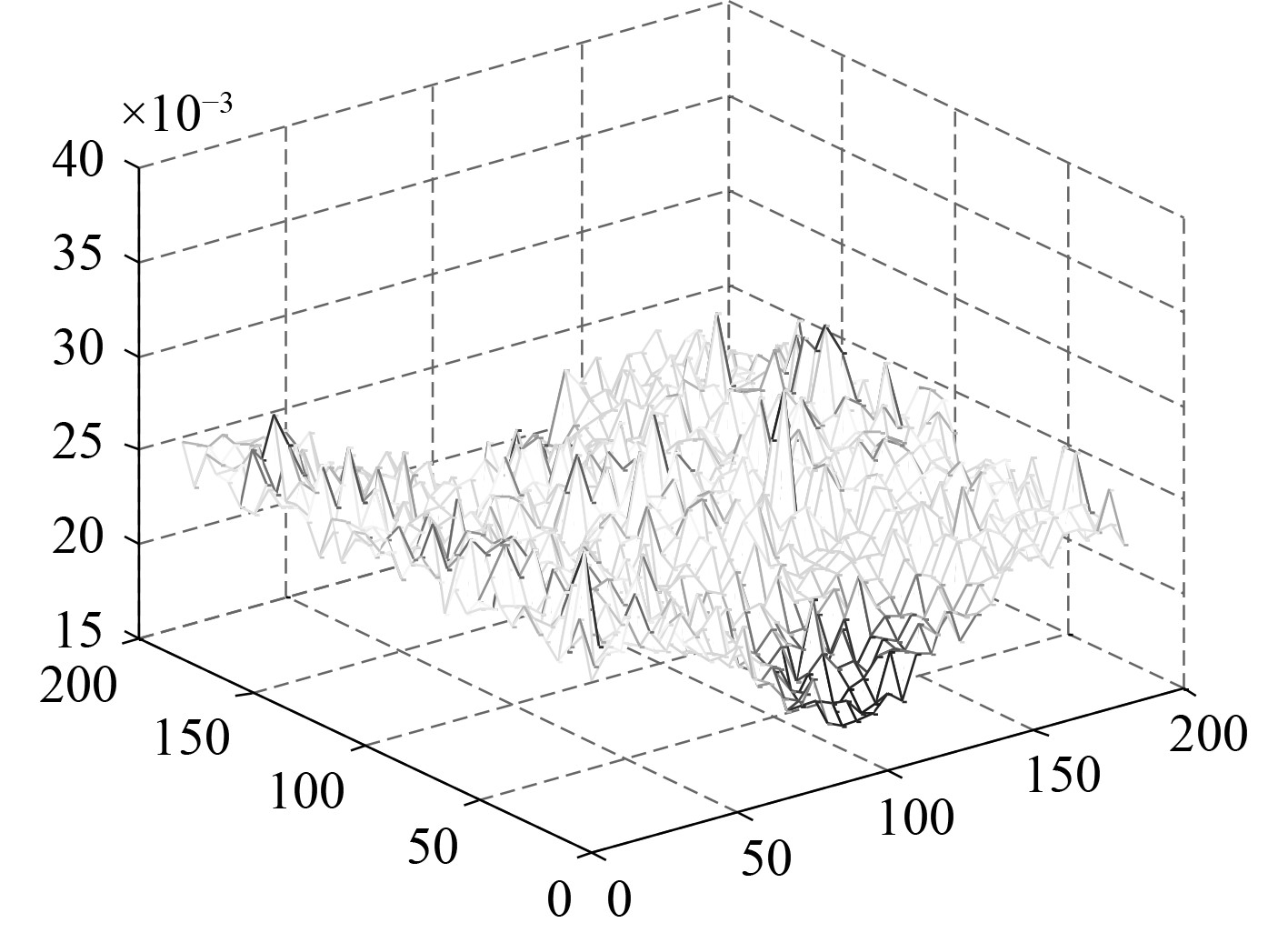
|
图 6 姿态误差引起的虚拟载波相位计算误差 Fig. 6 Effect of attitude error on virtual carrier phase |
实验测试分为2个环境,如图7所示。
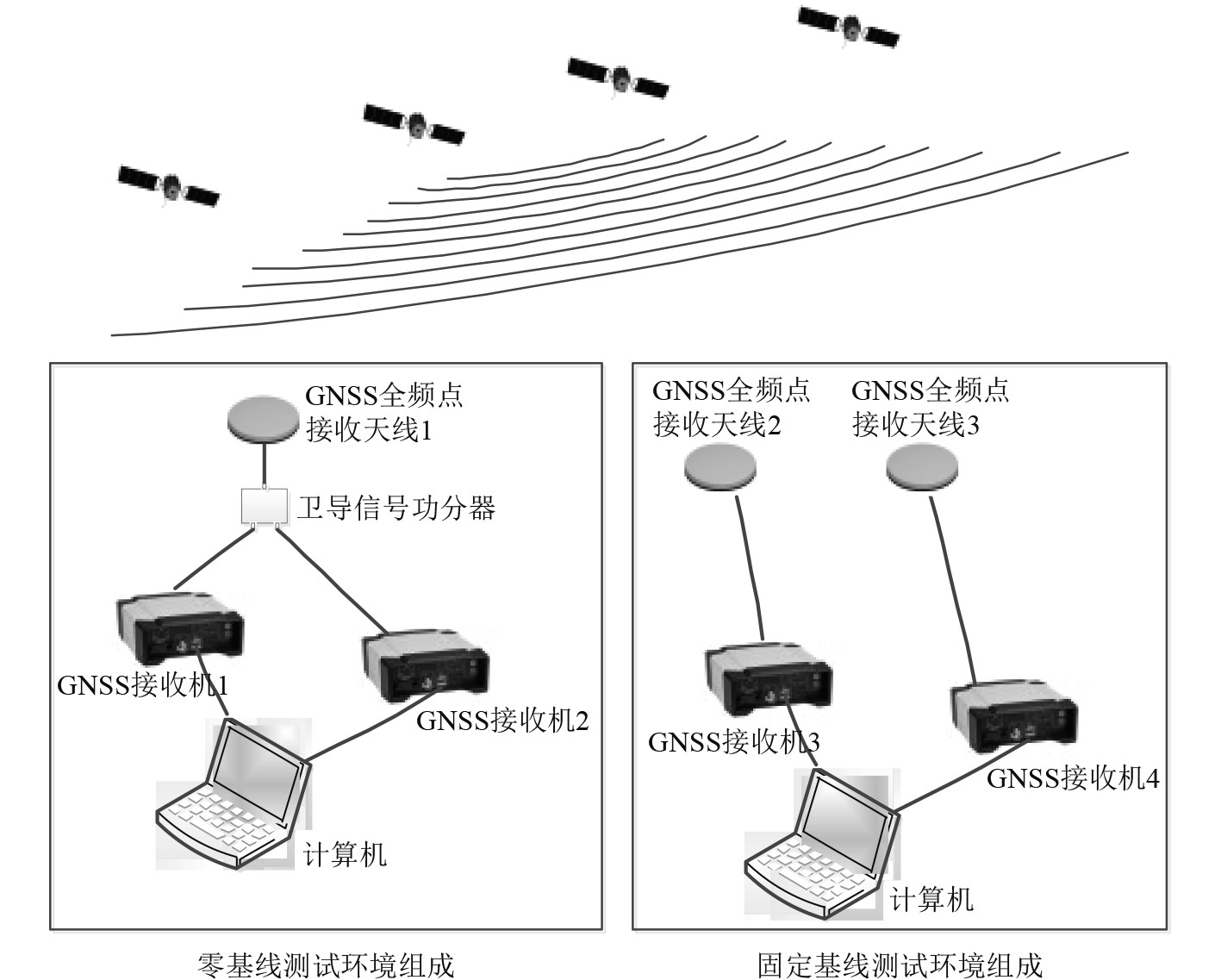
|
图 7 试验系统基本组成 Fig. 7 Basic constent of the experiment |
码载波分离度反映了接收机伪码观测与载波观测的一致性,受电离层影响,一般其值大小反映电离层变化率和多径变化率。在电离层稳定和无多径条件下,其值维持在微小量级,说明载波和伪码具有良好的一致性。因此,在相位和伪码观测虚拟场景中,可以采用码-载波分离度检测载波和伪码的一致性。
采用滑动几何平均的方法来估计码-载波偏离,固定平均的算法如下:
| $ Dvg{c_{m,n}}\left( k \right) = \left( {{\tau _d} - {T_s}} \right)/{\tau _d}.Dvg{c_{m,n}}\left( {k - 1} \right) + 1/{\tau _d}.d{z_{m,n}}\left( k \right) ,$ |
其中,
从图8可以看出,在进行观测虚拟前,码-载波分离度保持在1 mm以内,说明此时无异常电离层以及多径的存在。在进行载波和伪码虚拟观测生成后,码载波分离度仍然保持在1 mm以内,说明观测量的虚拟生成,未改变伪码和载波的一致性,与虚拟观测生成前保持在同等精度。
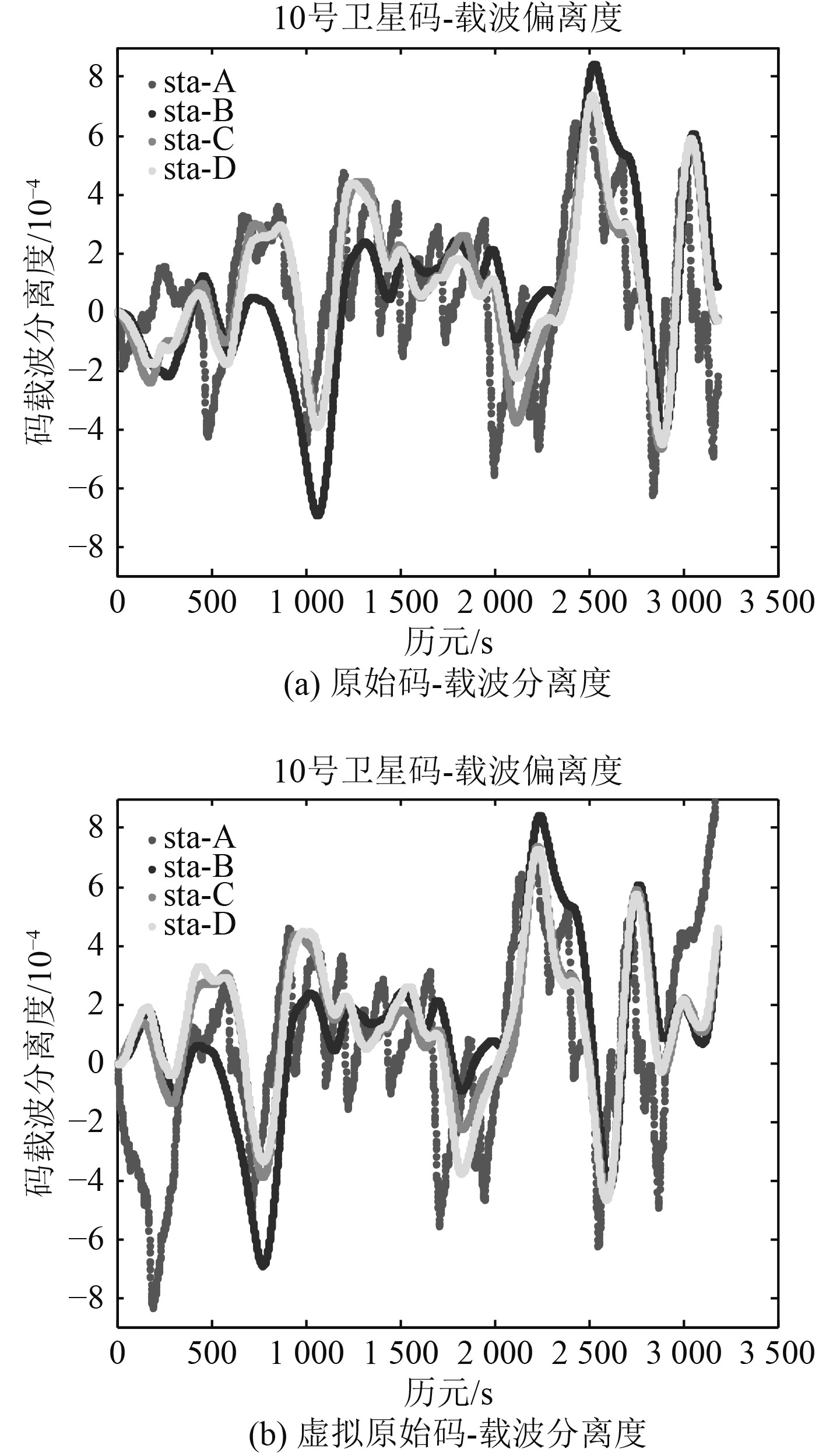
|
图 8 码-载波观测分离度 Fig. 8 Code and carrier phase divegence |
码载波分离度计算,证明伪码和载波生成上未发生分离,至于载波绝对值是否准确,采用基线测试的方法进行验证。
3.2 载波虚拟RTK动态测试由于实际环境中对于严格约束下的舰船参考站位置布局的接收机数据采集困难,因此考虑逆向数据生成,基准站Base和移动站Rove位于O点进行GNSS观测数据采集,将移动站Rove观测虚拟到舰船布站位置A,B,C,D,而后基于差分计算基准站和虚拟移动站观测差分计算得到的基线OA,OB,OC,OD矢量是否满足已知标定结果的精度,及检测模糊度固定性能指标,以验证虚拟伪距和载波满足一致性的前提要求。
3.2.1 载波虚拟零基线动态测试按照图7的系统组成,动态条件下采集接收机原始数据,进行接收机双差载波相位差分,结果如图9所示。
|
图 9 零基线双站观测差分基线计算 Fig. 9 Rtk baseline computation for zero-baseline stations |
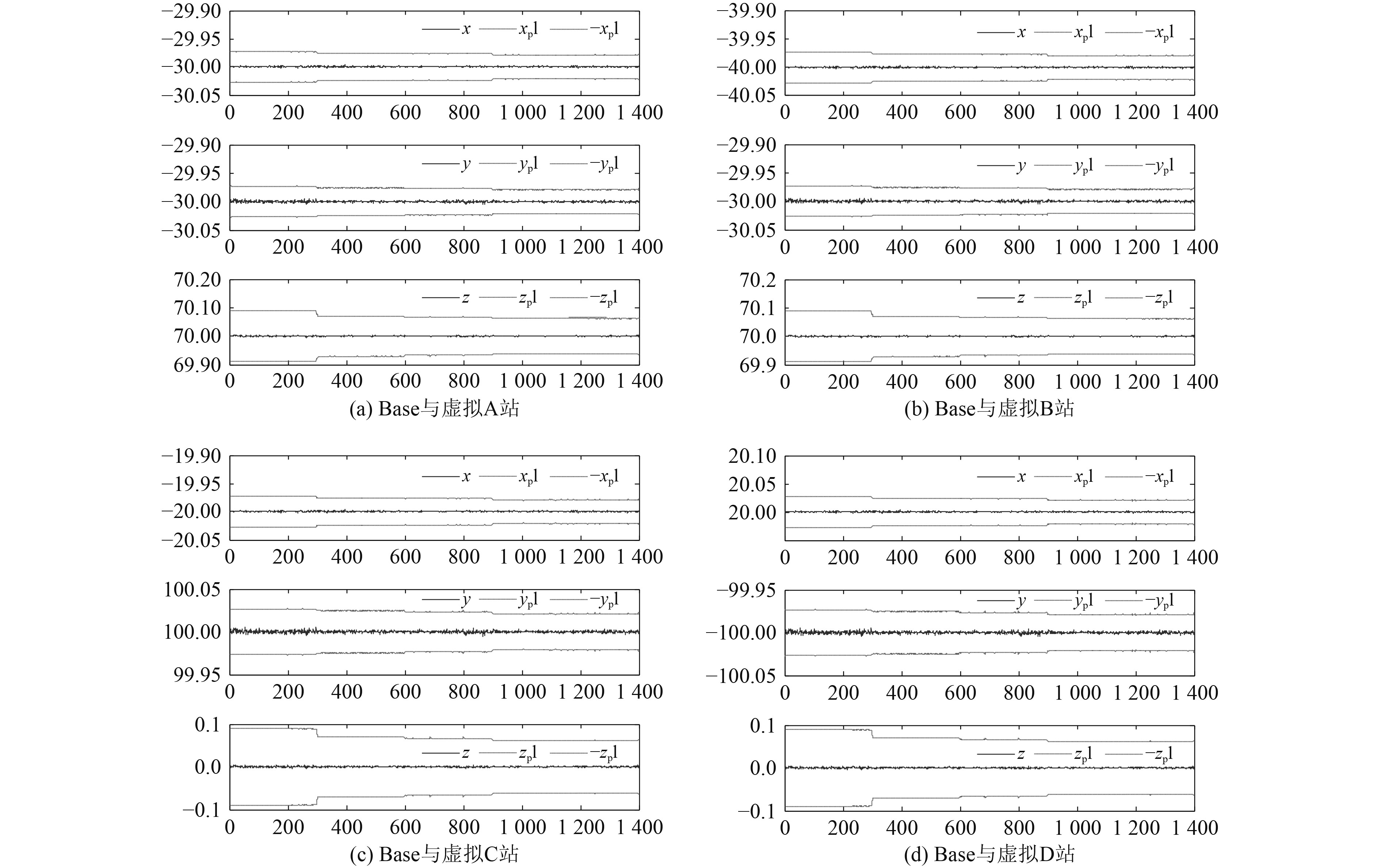
载波相位虚拟到A,B,C,D点后,进行基站与虚拟站间RTK计算。数据采集周期为0.1 s,采集1400个历元,进行站间差分。
动态多站虚拟观测进行载波相位差分的精度和差分性能统计结果,如表1所示。
|
|
表 1 静态虚拟站BDS差分精度与性能统计 Tab.1 static virtual station rtk position precesion |
按照图7的系统组成,固定基线动态场景条件下,采集接收机原始数据,进行接收机双差载波相位差分,结果如图10所示。
|
图 10 基站与虚拟站观测差分三维基线矢量 Fig. 10 Rtk relative position of virtual station to base station |
为了后期便于对比,将移动站的载波相位虚拟ECEF坐标系下固定基线的A,B,C,D点,而后进行基站与虚拟站间RTK计算。数据采集周期为0.1 s,采集9000个历元的差分。
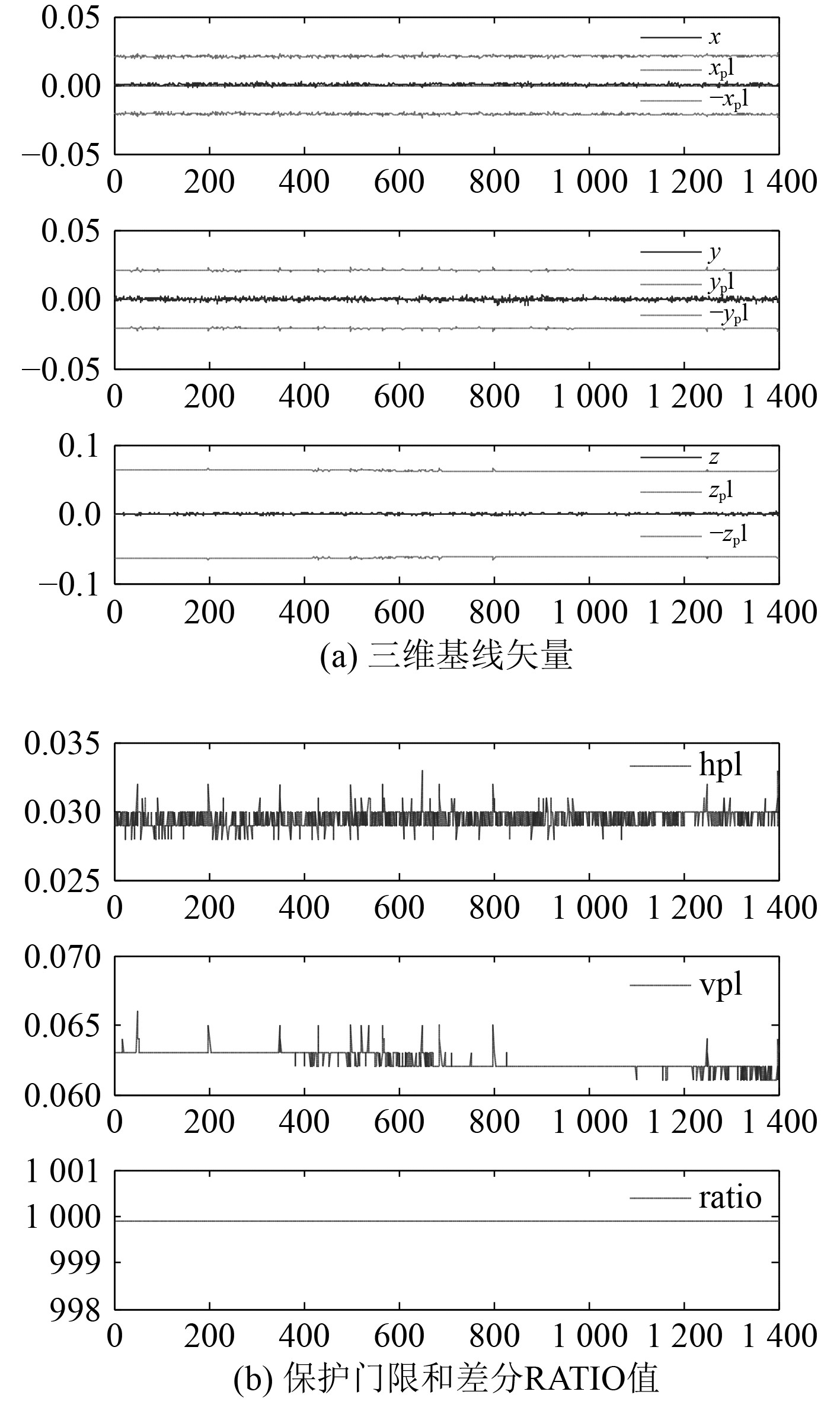
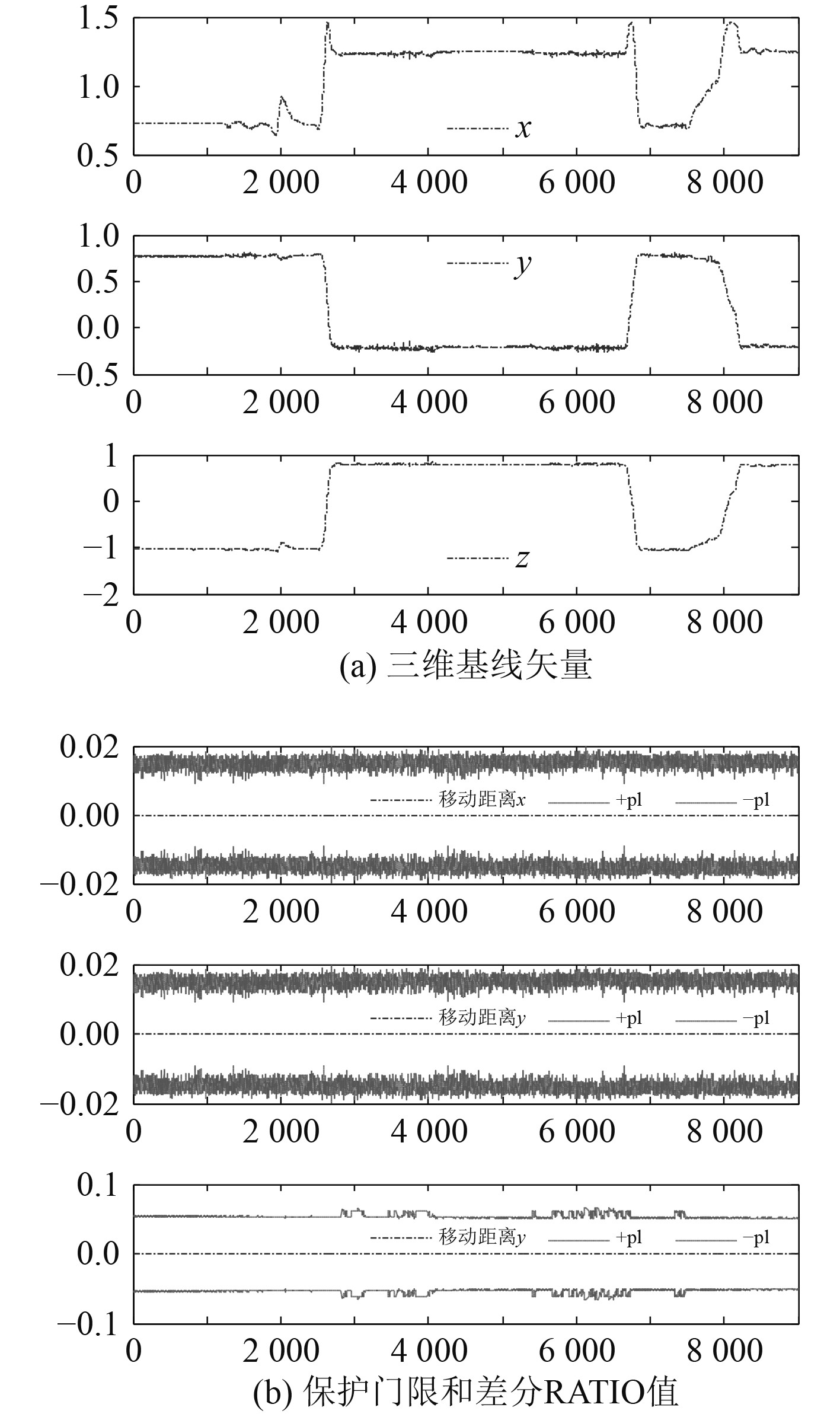
虚拟后观测相对于基站的的三维矢量和基线保护门限如图11所示,观测虚拟偏移如图12所示
|
图 11 三维基线与保护门限 Fig. 11 Baseline and protection level |
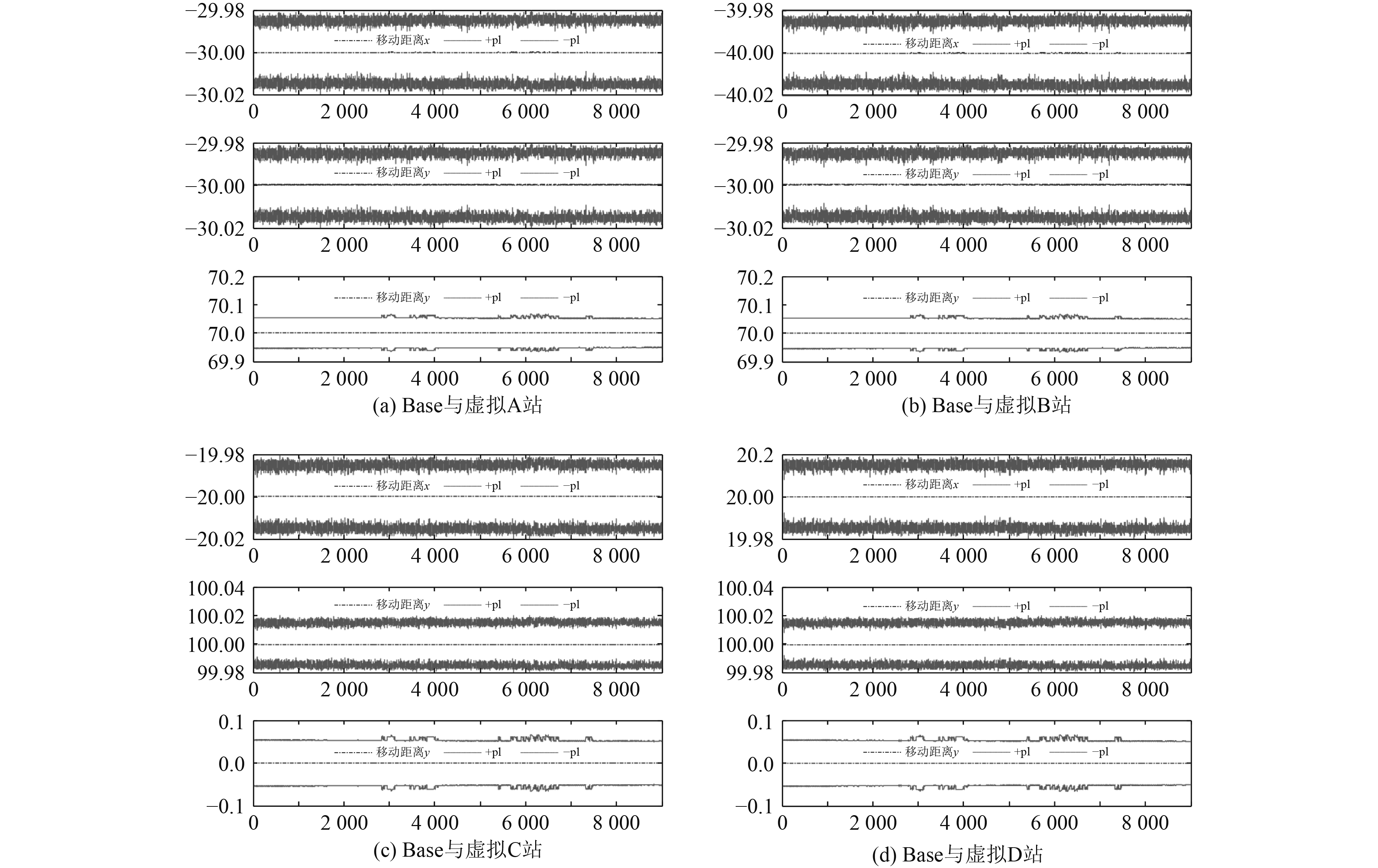
|
图 12 观测虚拟偏移三维矢量 Fig. 12 Virtual station position offset |
由于进行虚拟后,基线不具备固定性,而固定基线的虚拟中,移动站的偏移为固定已知量。因此,在进行性能统计时,主要采用虚拟基线偏移变化量与设定的基线偏移量作为统计量,统计结果如表2所示。
|
|
表 2 动态虚拟站BDS差分精度统计 Tab.2 Dynamic virtual station rtk position precesion |
提出载波和伪距虚拟到同一个着舰参考点的方法,可在此基础上建立运动载体不同位置观测的一致性。对影响载波相位虚拟观测精度的因素进行了分析和仿真,仿真结果表明,提出的载波虚拟方法能够保持相位的精度,最大的影响因素为载体上布站基线长度和姿态误差。针对虚拟载波观测的精度检验,提出采用基于码-载波分离度检验与伪码的一致性和通过多虚拟站的差分基线闭环检验相位精度。仿真结果证明在静态和动态条件下,该虚拟站技术能够保证厘米级差分能力,不降低载波相位差分的精度和差分性能。
| [1] |
喻思琪, 张小红. 卫星导航进近技术进展[J]. 航空学报, 2019, 40(3): 16-37. |
| [2] |
杨文辉, 周保军. LAAS地面系统中多基准一致性检验算法的分析[J]. 电子学报, 2006, 34(3): 469-471. DOI:10.3321/j.issn:0372-2112.2006.03.019 |
| [3] |
GANG Xie. Optimal on-airport monitoring of the integrity of gps-based landing systems[D]. Stanford University, 2004.
|
| [4] |
梁宸宇, 张世铎. 一种基于改进无监督学习的北斗多参考一致性监测算法[C]// China Satellite Navigation Conference. 2018.
|
| [5] |
李晓宇, 郑坤. 海基精密进近完好性监测体系与算法[J]. 测绘科学与工程, 2015, 35(4): 57-61. |
| [6] |
LI Liang. High accuracy tightly-coupled integrity monitoring algorithm for map-matching[J]. GPS Solut, 2012, (16): 209−220.
|
| [7] |
王官龙, 崔晓伟, 陆明泉. 北斗三频海基JPALS无故障导航算法[J]. 航空学报, 2017, 38(12): 321-340. |
| [8] |
原彬, 王晓旺. 海基JPALS系统故障监视处理技术分析[J]. 现代导航, 2017, 3: 162-165. DOI:10.3969/j.issn.1674-7976.2017.03.002 |
| [9] |
FENG Shao-jun, WASHINGTON O. Integrity monitoring for carrier phase ambiguities[j]. The Journal of Navigation, 2012, 65: 41−58.
|
| [10] |
LI Hui, GAO Shuang, LI Liang. Real time precise relative positioning with moving multiple Reference Receivers[J]. Sensor, 2018, 18, 2109.
|
 2022, Vol. 44
2022, Vol. 44
