船用舌阀是船舶系统管路密封的重要组成部分,对系统功能的实现和系统安全有着直接的影响。根据船用舌阀的使用条件,在选用标准舌阀不能满足使用要求的情况下,设计单位需要研制非标舌阀,根据工作介质压力、系统管路通径、材料性能参数等对舌阀进行设计计算。以往舌阀的设计计算采用解析法进行,需要对结构进行较大程度的简化,在应力校核时,只能得到局部的应力值,无法得到应力分布和各部位变形趋势等与阀门承压能力、密封性能密切相关的数据。随着数值计算分析技术的发展,对船用舌阀壳体结构设计方案进行有限元计算分析,预测和校核在受力状态下结构的合理性,为产品设计及改进提供依据,是传统设计方法的有效补充。
本文对一种船用舌阀的设计方案,进行三维有限元分析,得出在预紧力和工作载荷的共同作用下,壳体发生的应力和变形,预测其将对承压能力、密封产生的影响,根据计算结果,对设计方案进行改进。
1 舌阀结构图1所示的船用舌阀设计方案属于一种旋启式阀门,其主要由舌阀本体和传动机构2个部分组成。舌阀本体主要包括:壳体、冷却水套、阀座、阀盖等;传动机构主要包括:传动轴、杠杆、阀盘等。阀门的阀盘和阀座密封面为平面金属硬密封。

|
图 1 舌阀结构简图 Fig. 1 The structural of the flap |
阀门的工作原理是:在阀盘开启时,系统管路处于排气的状态,阀门近似不承压状态;在阀盘关闭压紧阀座密封面形成密封时,系统管路和整个阀腔内将注满海水,阀门处于承压状态,整个阀体内腔需要满足承压状态下的密封要求,为满足设计要求,对该状态下阀门的受力情况进行有限元分析计算。
2 有限元模型的建立对外部载荷引起的结构应力和应变进行计算,采用的分析方法是有限元法中的结构静力学分析功能。其依据的原理是:
| $ {\boldsymbol{K}} \times {\boldsymbol{U}} = F。$ | (1) |
其中:K矩阵代表着结构整体的总刚度;U矩阵代表着节点位移向量;F矩阵代表着节点载荷向量[1]。
对舌阀结构进行合理简化以建立有限元模型:舌阀的主壳体整体看作分析对象,建立三维实体模型,然后进行网格划分。阀座是通过紧固件与阀体连接的,将阀盘、阀座、杠杆、传动轴等装配件,其影响直接以力的形式作用在分析对象上。
3 边界条件有限元计算的关键一步是施加位移和力的边界条件。施加边界条件的方法根据有限元网格模型是否是在几何实体模型的基础上建立而分为2种[2]。
早期计算中对于有限元网格模型不是在几何实体模型的基础上建立的,需要进行人工计算将边界条件移置转换,然后将边界条件的等效计算值施加在有限元模型单元节点上。
现在计算中有限元网格模型可以在几何实体模型的基础上建立,将位移和力的边界条件直接添加在几何实体模型上,由相关计算软件完成边界条件的移置转换,使较复杂的边界条件计算和添加变得易于实施。本文进行的有限元分析就是将边界条件直接施加在基于实体几何模型建立的网格模型之上[1]。
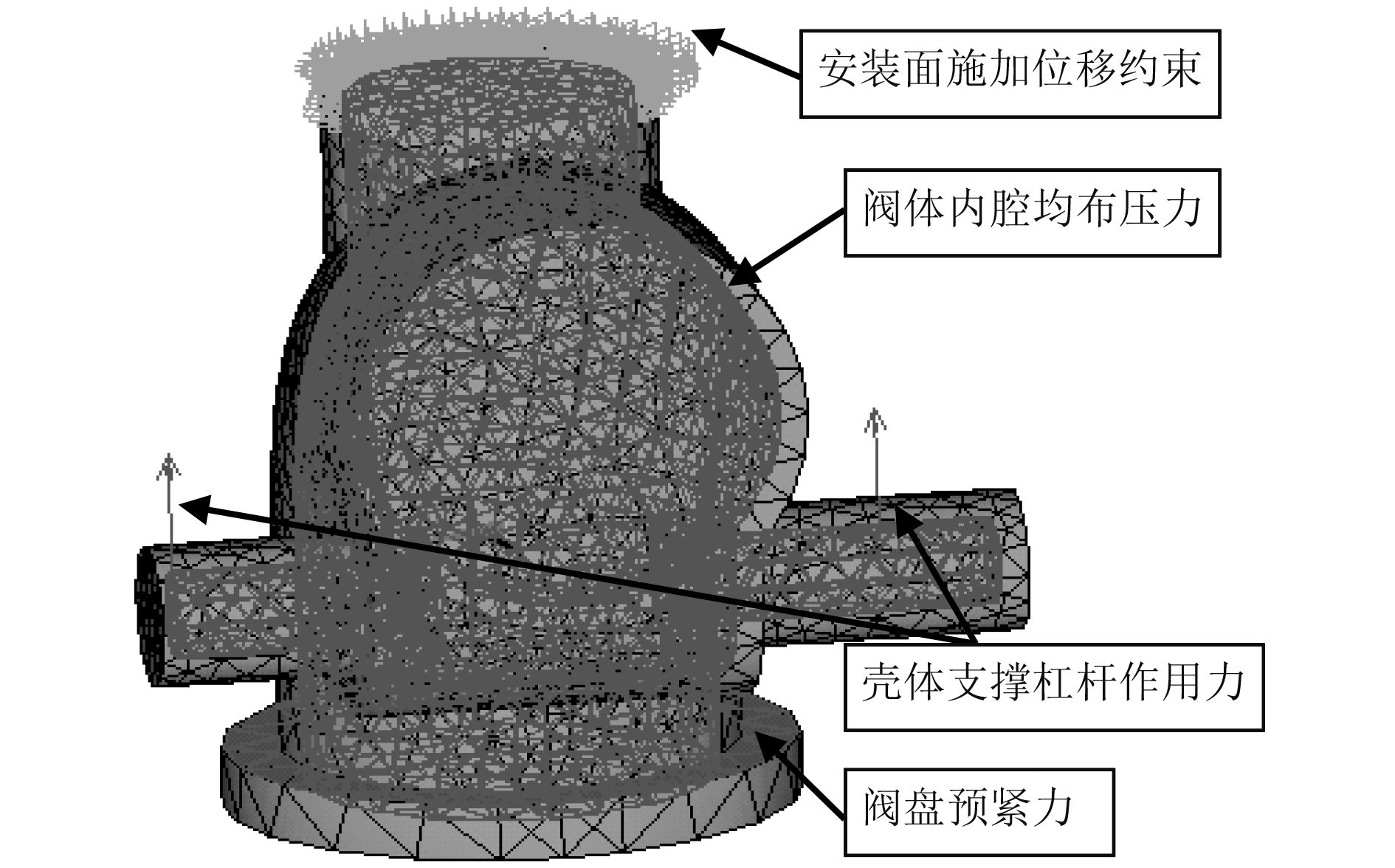
舌阀通过排气出口端法兰安装固定在舌阀座架上,因此约束壳体排气出口端面X/Y/Z三个方向的位移约束。舌阀壳体受力主要有:阀体内腔表面所受的海水均布压力、压紧阀盘的预紧力和传动轴壳体作为支撑所受杠杆的作用力。其中压紧阀盘的预紧力通过阀座最后作用在排气进口端法兰面上;为了模拟阀体内腔承压状况,将模型中排气进出口和与阀盖连接口均用盲板封闭,内腔表面施加均布载荷,壳体约束和载荷见图2。
|
图 2 舌阀有限元模型所受约束和载荷 Fig. 2 Constraints and loads on the finite element model of flap valve |
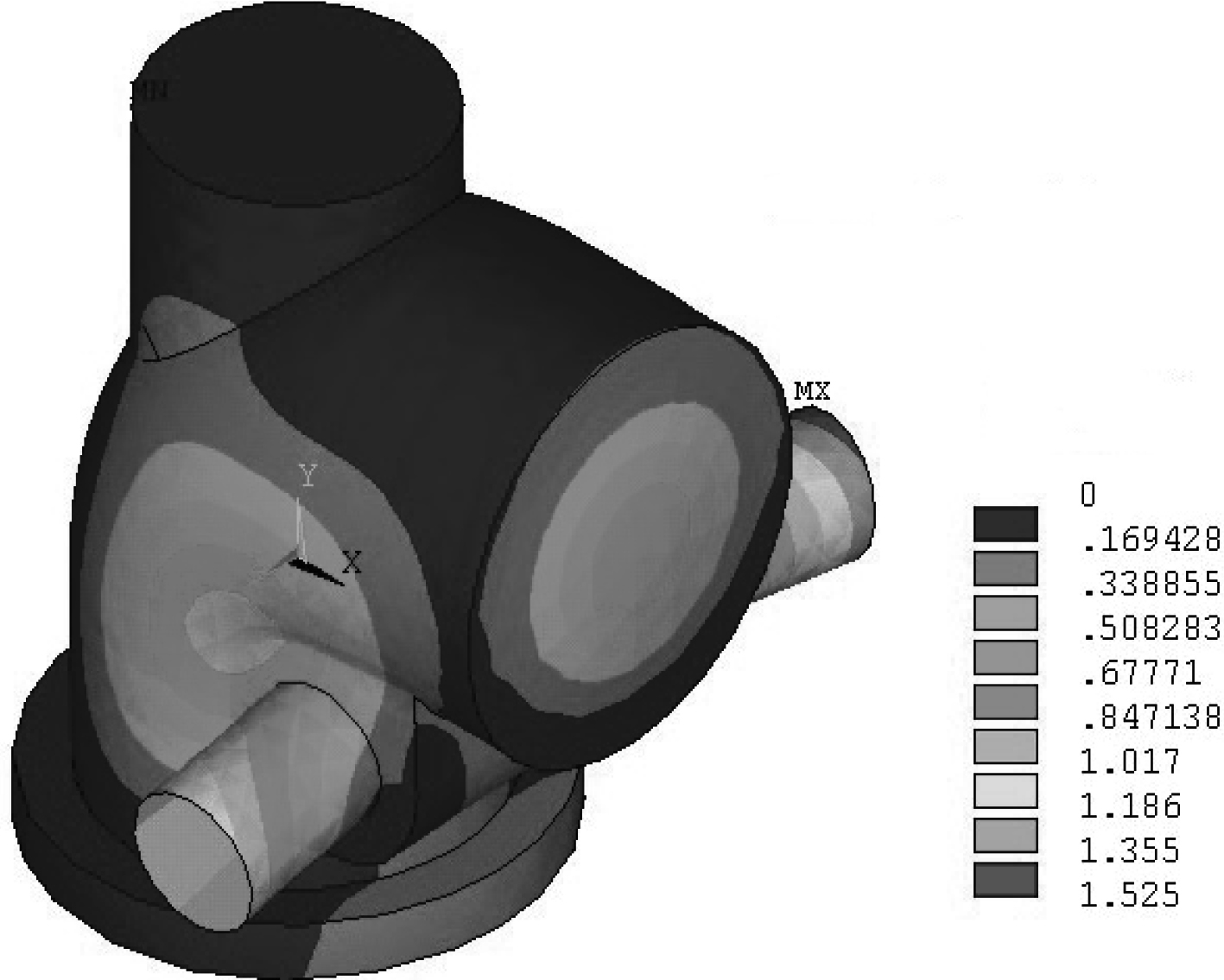
计算得到舌阀壳体变形情况如图3所示。变形有如下特点:部位比较集中,较大的变形主要出现在传动轴支承壳体与主壳体焊接处周围;最大变形发生在传动轴支承壳体两端,两端变形大小不完全对称,变形方向为向x轴正方向和y轴负方向,最大值约为1.5 mm,经分析认为产生最大变形的原因是该部位受力较大且局部产生了应力集中,轴支承壳体两端近似为悬臂结构,内部受高压作用,外部又缺乏支撑。
|
图 3 舌阀总变形量图 Fig. 3 Total deformation of flap valve |
有限元计算得到了舌阀壳体在x,y,z方向的主应力和等效应力。其中等效应力的计算公式见式(2),是材料力学中第四强度理论的表征值,将计算出的等效应力与材料的许用应力进行比较,可以分析判断材料的强度现状,适合于通常以屈服形式失效的金属材料的应力分析[1]。
| $ \sqrt{\frac{1}{2}\left[\left(\sigma_{1}-\sigma_{2}\right)^{2}+\left(\sigma_{2}-\sigma_{3}\right)^{2}+\left(\sigma_{3}-\sigma_{1}\right)^{2}\right]} \leqslant\left[\sigma_{x}\right]。$ | (2) |
式中:σ1,σ2,σ3分别为x,y,z方向主应力值;σs为屈服极限。
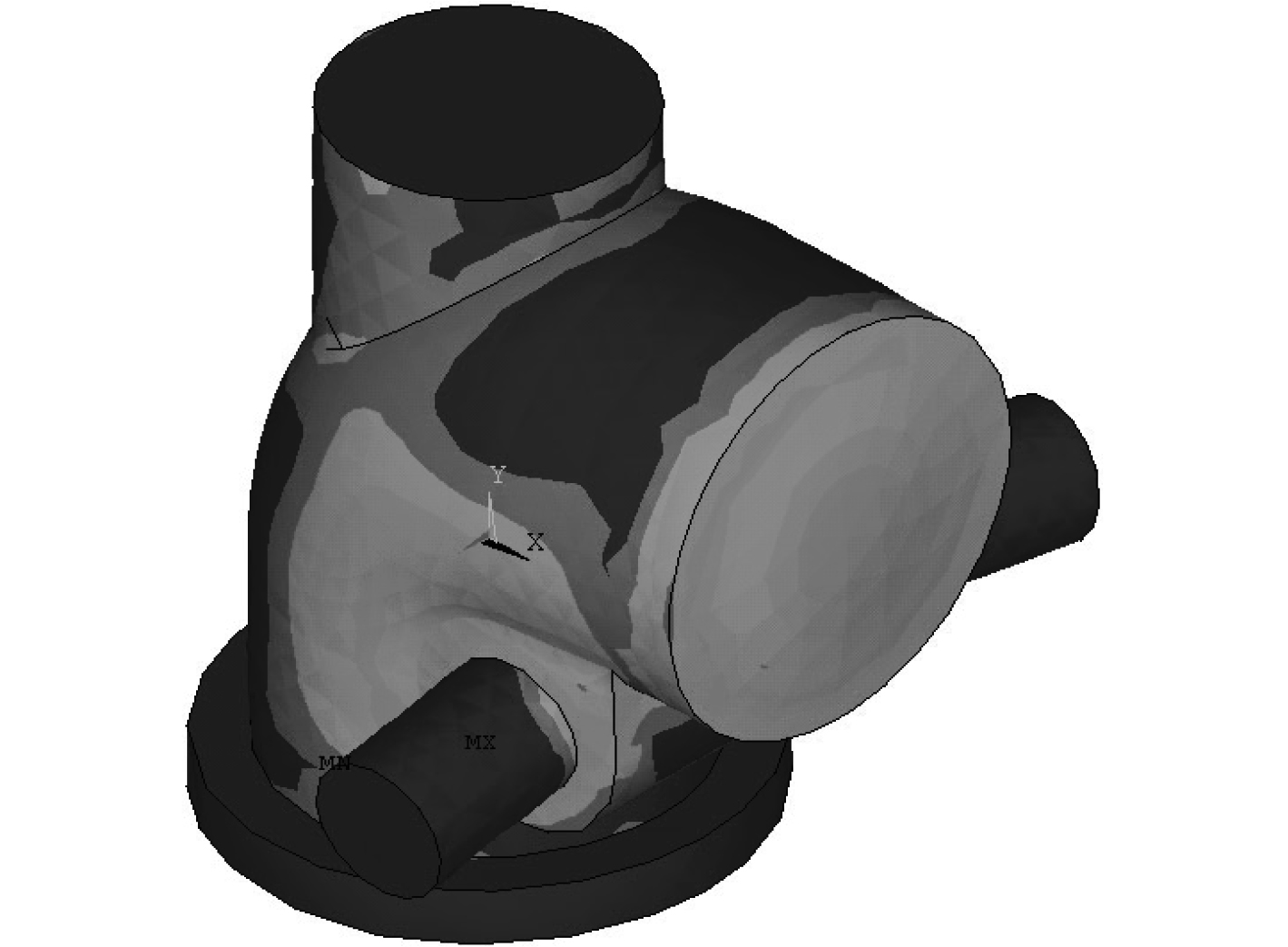
舌阀的平均等效应力云图如图4所示,舌阀承受应力比较均匀,变形较大的支承轴壳体与主壳体连接处同样应力也较大。强度校核表明壳体各部分的安全系数满足要求。
|
图 4 舌阀应力 Fig. 4 Flap valve stress |
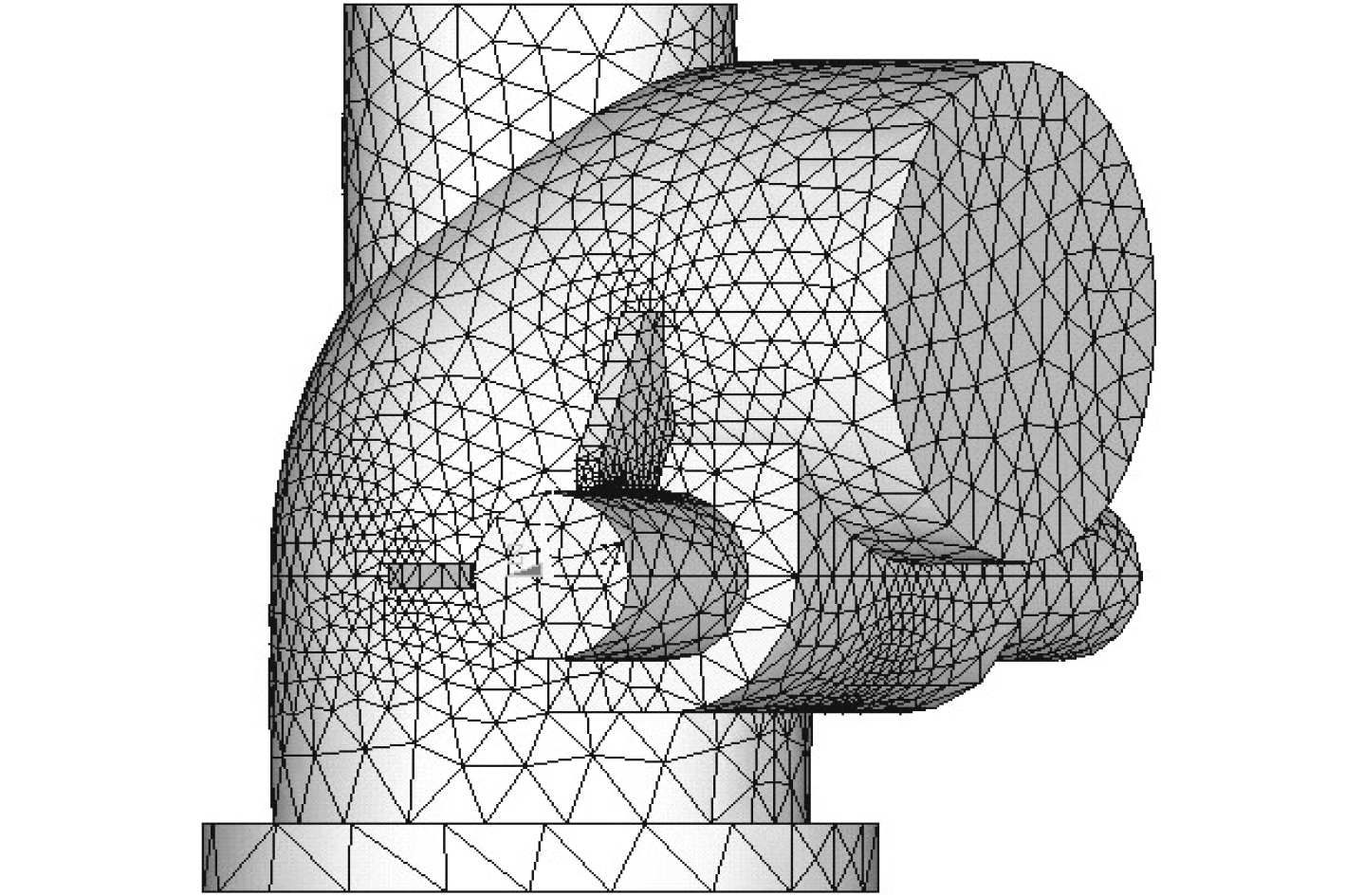
针对支承轴壳体两端出现较大变形,支承轴壳体与主壳体连接处变形和应力都比较大的特点,采取的措施是加固支承轴壳体,在支承轴壳体与主壳体间焊接筋板,每侧两块筋板呈90°,布置在壳体变形方向的反方向,即x轴负方向和y轴正方向,改进后的舌阀模型如图5所示,舌阀总变形量如图6所示。
|
图 5 改进后舌阀加筋板模型 Fig. 5 Improved flap valve stiffened model |
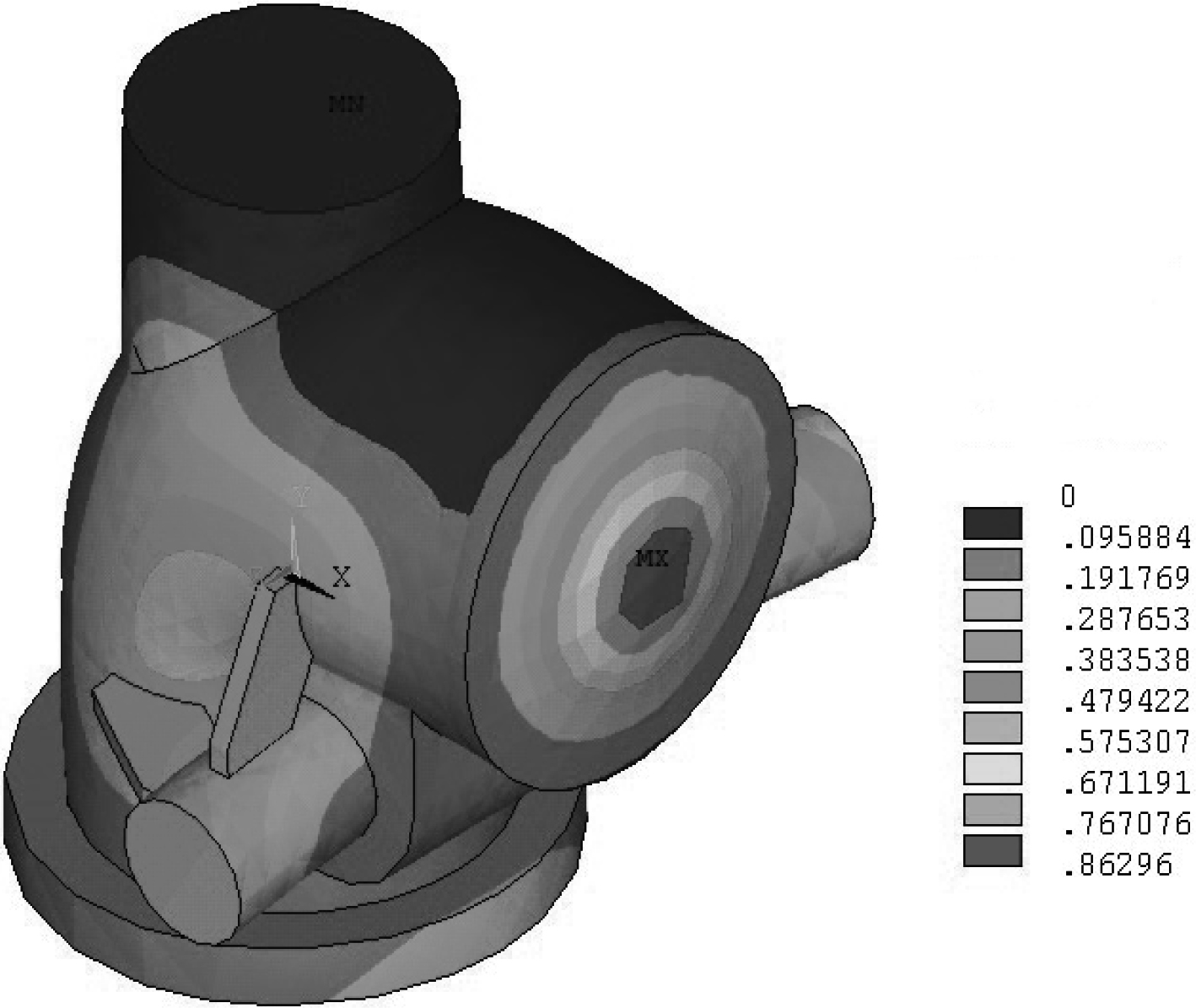
|
图 6 改进后舌阀总变形量 Fig. 6 Total deformation of flap |
在船用舌阀的研制过程中,利用有限元分析技术对阀门在一定承压环境下的结构刚度、强度进行较为精确的分析和校核,根据分析结果对阀门结构进行优化设计,对易产生变形的薄弱部位进行加固,优化后的阀门结构更趋合理、密封性能好、满足设计要求。这种方法对具有类似环境条件下其他阀门设备的研制具有借鉴、参考价值。
| [1] |
孙春鹏, 柴油机整体式喷油器设计及有限元分析 [D]. 武汉: 华中科技大学, 2004.
|
| [2] |
廖日东, 左正兴, 樊利霞, 等. 发动机零部件有限元技术应用的新进展[J]. 内燃机学报, 1999, 17(2): 190-197. LIAO Ridong, ZUO Zhengxing, FAN Lixia, et al. Development in the finite element technology application for engine components [J] Transactions of CSICE, 1999, 17(2): 190-197. |
| [3] |
SIENZ J. Computational modelling of 3D objects by using fitting techniques and subsequent mesh generation[J]. Computers & Structures, 2000, 78: 397-413. |
| [4] |
GUNAY E. Composite design of the diesel engine cylinder with finite element analysis[J]. Computers and Structures, 2000, 75: 117-134. DOI:10.1016/S0045-7949(99)00092-9 |
| [5] |
PISANI S. R., RENCIS J. J.. Investigating CURVIC coupling behavior by utilizing two and three dimensional boundary and finite element methods[J]. Engineering Analysis with Boundary Elements, 2000, 24: 271-275. DOI:10.1016/S0955-7997(99)00057-0 |
| [6] |
何建孟, 球阀和闸阀结构强度的阀门设计与有限元分析[D]. 大连: 大连理工大学, 2016.
|
| [7] |
周玮, 中高压法兰蝶阀阀体结构强度的有限元分析[J]. 机械设计与制造, 2010(7) : 218−220. ZHOU Wei, Finite element analysis of structural strength of medium and high pressure flange butterfly valve body[J]. Machinery Design & Manufacture, 2010(7) : 218−220. |
| [8] |
金建海, 冷文浩. 船舶有限元网格自动生成技术研究[J]. 舰船科学技术, 2009(11): 14-16. JIN Jianhai, LENG Wenhao. Research on ship FEM generation technologies[J]. Ship Science and Technology, 2009(11): 14-16. |
| [9] |
杜平安. 有限元网格划分的基本原则[J]. 机械设计与制造, 2000(1): 34-36. DU Pingan. The basic principle of finite element mesh generation[J]. Machinery Design & Manufacture, 2000(1): 34-36. DOI:10.3969/j.issn.1001-3997.2000.01.016 |
| [10] |
陈精一, 蔡国忠. 电脑辅助工程分析: ANSYS使用指南[M]. 北京: 中国铁道出版社, 2001年: 9−14.
|
 2022, Vol. 44
2022, Vol. 44
