我国大型水面舰艇的核心设备和关键设备是大功率轴流压气机[1]。舰船大功率轴流压气机在长期仿制和跟踪过程中,自主设计能力较低,存在专业化设计准则缺失、指标较低和体系不完善等问题。现代舰船大功率轴流压气机逐渐向高喘振裕度、效率和平均级压比的方向发展,对压气机控制方法提出了更高的要求[2]。在设计燃气轮机的过程中压气机的设计技术属于关键技术,压气机的性能直接影响着燃气轮机的整机性能,因此急需设计一种有效的舰船大功率轴流压气机控制方法。
文献[3]提出基于动态边界的轴流压气机控制方法,该方法将出口静压和转速作为控制参数,在动态边界条件的基础上通过二阶向后欧拉法对Navier-Stokes方程组进行求解,获得压气机的内部非定常流场特征和过渡态性能,根据上述性能对压气机进行控制,该方法没有对压气机的工作过程进行数值模拟,存在绝热效率低和总压损失系数高的问题。文献[4]提出基于弯掠参数控制的压气机控制方法,该方法通过数值模拟方法计算压气机原型性能,选取B样条和Bezier样条对控制点个数进行拟合,结合遗传算法和人工神经网络算法通过控制叶片的弯掠特性参数实现压气机的控制,该方法在数值模拟过程中没有进行加速收敛处理,导致控制所需的时间较长,存在控制时间长的问题。为了解决上述方法中存在的问题,提出舰船大功率轴流压气机智能控制方法。
1 数值模拟及控制优化目标函数 1.1 数值模拟1)控制方程
Navier-Stokes方程在直角坐标系下可以通过下述矢量形式进行描述:
| $ \frac{\partial }{{\partial t}}\vec U + \nabla {\vec F_I} + \nabla {\vec F_V} = \vec Q。$ | (1) |
式中:
在直角坐标系下上述参数可以通过分量形式进行描述:
| $ \left\{ \begin{gathered} {{\vec F}_I} = {F_{I1}}\vec i + {F_{I2}}\vec j + {F_{I3}}\vec k,\hfill \\ {{\vec F}_V} = {F_{V1}}\vec i + {F_{V2}}\vec j + {F_{V3}}\vec k,\hfill \\ \vec U = \left[ {\begin{array}{*{20}{c}} {\bar \rho } \\ {\bar \rho {w_1}} \\ {\bar \rho {w_2}} \\ {\bar \rho {w_3}} \\ {\bar \rho E} \end{array}} \right],{F_{Ii}} = \left[ {\begin{array}{*{20}{c}} {\bar \rho {w_i}} \\ {\bar \rho {\delta _{1i}} + \bar \rho {w_i}{w_1}} \\ {\bar \rho {\delta _{2i}} + \bar \rho {w_i}{w_2}} \\ {\bar \rho {\delta _{3i}} + \bar \rho {w_i}{w_3}} \\ {(\bar P + \bar \rho E){w_i}} \end{array}} \right],\hfill \\ - {F_{Vi}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{\tau _{i1}}} \\ {{\tau _{i2}}} \\ {{\tau _{i3}}} \\ {{q_i} + {w_j}{\tau _{ij}}} \end{array}} \right],Q = \left[ {\begin{array}{*{20}{c}} 0 \\ { - \rho [2\vec \omega \vec w + (\vec \omega \times \vec \omega \vec r)]} \\ {\rho \vec w(0.5{\omega ^2}{r^2})} \end{array}} \right]。\hfill \\ \end{gathered} \right. $ | (2) |
式中:
| $ \left\{ \begin{gathered} {\delta _{ij}} = \left\{ {\begin{array}{*{20}{c}} 0,&{i = j},\\ 1,&{i \ne j},\end{array}} \right. \hfill \\ {\tau _{ij}} = {({\tau _{ij}})_l} + {({\tau _{ij}})_i} = (\mu + {\mu _i})\left[ {\frac{{\partial {w_i}}}{{\partial {x_j}}} + \frac{{\partial {w_j}}}{{\partial {x_i}}} - \frac{{2(\nabla \vec w){\delta _{ij}}}}{3}} \right],\hfill \\ {q_i} = (\kappa + {\kappa _i})\frac{\partial }{{\partial {x_i}}}T。\hfill \\ \end{gathered} \right. $ | (3) |
引入气体状态方程,封闭整个方程,理想气体存在下式:
| $ P = \rho RT。$ | (4) |
通过合适的湍流模型求解涡粘性系数
2)湍流模型
S-A模型从量纲或经验分析出发属于线性涡粘性模型[5-6],设
| $ {\mu _i} = \mu {f_{v1}},$ | (5) |
其中,函数
| $ {f_{v1}} = \frac{{{\chi ^3}}}{{{\chi ^3} + C_{v1}^3}},$ | (6) |
式中,
| $ \frac{{\partial \mu }}{{\partial t}} + \vec V \cdot \nabla \mu = \frac{{\{ \nabla [\mu + (1 + {c_{b2}})\mu ]\nabla \mu - \mu {c_{b2}}\Delta \mu \} + Q}}{\sigma }。$ | (7) |
式中:
由耗散项和生成项构成源项
| $ \left\{ \begin{gathered} Q = - \mu D(\mu ){\text{ + }}\mu P(\mu ),\hfill \\ \mu D(\mu ) = {c_{w1}}{f_w}{\left( {\mu /d} \right)^2},\hfill \\ \mu P(\mu ) = {c_{b1}}S\mu 。\hfill \\ \end{gathered} \right. $ | (8) |
生成项的表达式如下:
| $ \left\{ \begin{gathered} S = S{f_{v3}} + \frac{\mu }{{{k^2}{d^2}}}{f_{v2}},\hfill \\ {f_{v2}} = \frac{1}{{{{\left(1 + \chi /{C_{v2}}\right)}^3}}},\hfill \\ {f_{v3}} = \frac{{\left(1 + \chi {f_{v1}}\right)\left(1 - {f_{v2}}\right)}}{\chi }。\hfill \\ \end{gathered} \right. $ | (9) |
式中:
| $ \left\{ \begin{gathered} {f_w} = g{\left( {\frac{{1 + C_{w3}^6}}{{{g^6} + C_{w3}^6}}} \right)^{1/6}},\hfill \\ g = r + {c_{w2}}({r^6} - r)。\hfill \\ \end{gathered} \right. $ | (10) |
3)数值方法
舰船大功率轴流压气机智能控制方法选用Spalart-Allmaras湍流模型,在相对坐标系中采用有限体积差分格式求解三维雷诺平均Navier-Stokes方程。为了提高求解速度和求解精度,采用当地时间步长、隐式残差光顺和多重网格法进行加速收敛处理。
①当地时间步长
计算和求解过程中的时间步长通常选用当地时间步长,通过下式描述当地时间步长对应的无粘项:
| $ {\left( {\frac{{\Delta t}}{\varOmega }} \right)_I} = \frac{{CFL}}{{|\vec {\boldsymbol{w}}{{\vec {\boldsymbol{S}}}_i}| + |\vec {\boldsymbol{w}}{{\vec {\boldsymbol{S}}}_J}| + |\vec {\boldsymbol{w}}{{\vec {\boldsymbol{S}}}_k}| + \vec {\boldsymbol{c}}[|{{\vec {\boldsymbol{S}}}_i}| + |{{\vec {\boldsymbol{S}}}_j}| + |{{\vec {\boldsymbol{S}}}_k}|]}}。$ | (11) |
式中:
利用下式描述粘性项:
| $ \begin{split} {\left( {\frac{{\Delta t}}{\varOmega }} \right)_v} = &CFLVIS \cdot \Omega \rho /\{ \mu [|{{\vec {\boldsymbol{S}}}_i}{|^2} + |{{\vec {\boldsymbol{S}}}_j}{|^2} + |{{\vec {\boldsymbol{S}}}_k}{|^2}\} + \\ &2[|{{\vec {\boldsymbol{S}}}_i}{{\vec {\boldsymbol{S}}}_j}| + |{{\vec {\boldsymbol{S}}}_i}{{\vec {\boldsymbol{S}}}_k}| + |{{\vec {\boldsymbol{S}}}_k}{{\vec {\boldsymbol{S}}}_j}|]\}。\end{split} $ | (12) |
式中:
当给定有粘和无粘CFL数时,实际的当地时间步长可通过下式的计算得到:
| $ \left( {\frac{{\Delta t}}{\varOmega }} \right) = \min \left\{ {{{\left( {\frac{{\Delta t}}{\varOmega }} \right)}_v},{{\left( {\frac{{\Delta t}}{\varOmega }} \right)}_I}}\right\},$ | (13) |
当给定无粘CFL数时,当地时间步长可通过下式计算得到:
| $ \left( {\frac{{\Delta t}}{\varOmega }} \right) = {\left( {\frac{{\Delta t}}{\varOmega }} \right)_v}{\left( {\frac{{\Delta t}}{\varOmega }} \right)_I}\Bigg/\left[ {{{\left( {\frac{{\Delta t}}{\varOmega }} \right)}_v} + {{\left( {\frac{{\Delta t}}{\varOmega }} \right)}_I}} \right]。$ | (14) |
②隐式残差光顺
通常情况下隐式残差光顺加速收敛方法在使用过程中与Runge-Kutta方法结合使用,可通过下式进行描述:
| $ {U^{m + 1}} = {U^m} + {\alpha _m}\Delta tF({U^m}) + {\alpha _m}R({U^m}),$ | (15) |
式中,
| $ R = \left(I - {\varepsilon _i}\Delta _i^2\right)\left(I - {\varepsilon _j}\Delta _j^2\right)\left(I - {\varepsilon _k}\Delta _k^2\right)\tilde R,$ | (16) |
式中,
| $ {\varepsilon _l} = \frac{1}{4}\left[ {\frac{{{\sigma ^*}}}{{\sigma \left[1 + 0.0625\left(\lambda _j^*/\lambda _i^*\right) + \left(\lambda _k^*/\lambda _i^*\right)\right]}}} \right] - 1。$ | (17) |
式中:
③多重网格法
将多重网格技术应用在网格划分和数值模拟的计算过程中,加快收敛速度,提高计算效率,对固定网格缺陷进行修复[10-11]。
网格数在计算过程中通常满足
| $ \frac{{\partial {U^N}}}{{\partial t}} + {N_N}\left({U^N}\right) = 0,$ | (18) |
式中,
N-S方程在计算粗网格
| $ \frac{{\partial {U^N}}}{{\partial t}} + {N_N}\left({U^N}\right) = {F_L},$ | (19) |
式中,
| $ {F_L} = {N_L}\left(I_{L + 1}^L{U^{L + 1}}\right) + \hat I_{L + 1}^L\left[{F_{L + 1}} - {N_{L + 1}}\left({U^{L + 1}}\right)\right]。$ | (20) |
气动优化过程中通常不是单一的,对应的约束条件也是多样的,舰船大功率轴流压气机优化控制的数学表达式如下:
| $ \left\{ \begin{gathered} \min F(x),\hfill \\ F(x) = \{ {f_1}(X),{f_2}(X), \cdots ,{f_m}(X)\},\hfill \\ X = ({x_1},{x_2}, \cdots ,{x_k}),\hfill \\ {\rm{s.t}}.\left\{ {\begin{array}{*{20}{c}} {{c_i}(X) = 0},&{i \in E},\\ {{c_i}(X) \geqslant 0},&{i \in I}。\end{array}} \right. \hfill \\ \end{gathered} \right. $ | (21) |
式中:
舰船大功率轴流压气机智能控制方法采用标准人工蜂群算法对舰船大功率轴流压气机优化控制目标函数进行求解,实现舰船大功率轴流压气机的智能控制。
寻优过程一般情况下涉及的蜂群由3类蜜蜂构成,分别是侦察蜂、观察蜂和采蜜蜂[12]。蜜蜂总体在初始阶段分为两部分,一部分为观察蜂,另一部分为采蜜蜂。可行解即为采蜜蜂对应的采蜜源位置,可行解对应的适应度可以通过蜜源浓度进行描述。求解的具体过程如下:
1)对蜜源进行初始化处理。随机生成
| $ X_i^j = X_{\min }^j + rand(0,1)\left(X_{\max }^j - X_{\min }^j\right)。$ | (22) |
式中:
2)对蜜源初始浓度进行计算,即可行解相应的适应度,记录最佳值,按从大到小的顺序排序,将前半部分的蜜源适应度对应的蜜蜂作为采蜜蜂,观察蜂即为剩余的蜜蜂[13]。
3)利用下式在原蜜源附近搜索每只采蜜蜂周围存在的其他蜜源,并对蜜源对应的适应度进行计算,如果新蜜源对应的适应度比初始蜜源对应的适应度高,用新蜜源代替原始蜜源;如果新蜜源对应的适应度低于初始蜜源对应的适应度,开始新一轮的探索[14]。
| $ V_i^j = X_i^j + \varphi _i^j(X_i^j - X_k^j)。$ | (23) |
式中:
4)根据采蜜蜂所采蜜源适应度成比例的概率,通过俄罗斯轮盘赌法则选择蜜源,并在周围寻找新的蜜源。观察蜂在新探索蜜源适应度较高时转变为采蜜蜂,原蜜源被新蜜源所代替,观察蜂在新探索蜜源对应的适应度较低时进行下一次探索[15]。在下式的基础上观察蜂选择蜜源:
| $ P = \frac{{f({X_i})}}{{\displaystyle\sum\limits_m^{{N_e}} {f({X_m})} }}。$ | (24) |
式中:
5)如果观察蜂或采蜜蜂在探索过程中的探索次数超出设定的阈值且没有获取适应度较高的蜜源时,观察蜂或采蜜蜂转变为侦查蜂,通过上述过程生成新蜜源,侦察蜂在生成新蜜源后转变为采蜜蜂。
6)将最优蜜源记录下来,并转到步骤2中,当满足设定的循环条件时,获得最优蜜源位置,输出压气机优化控制目标函数的最优解,实现舰船大功率轴流压气机的智能控制。
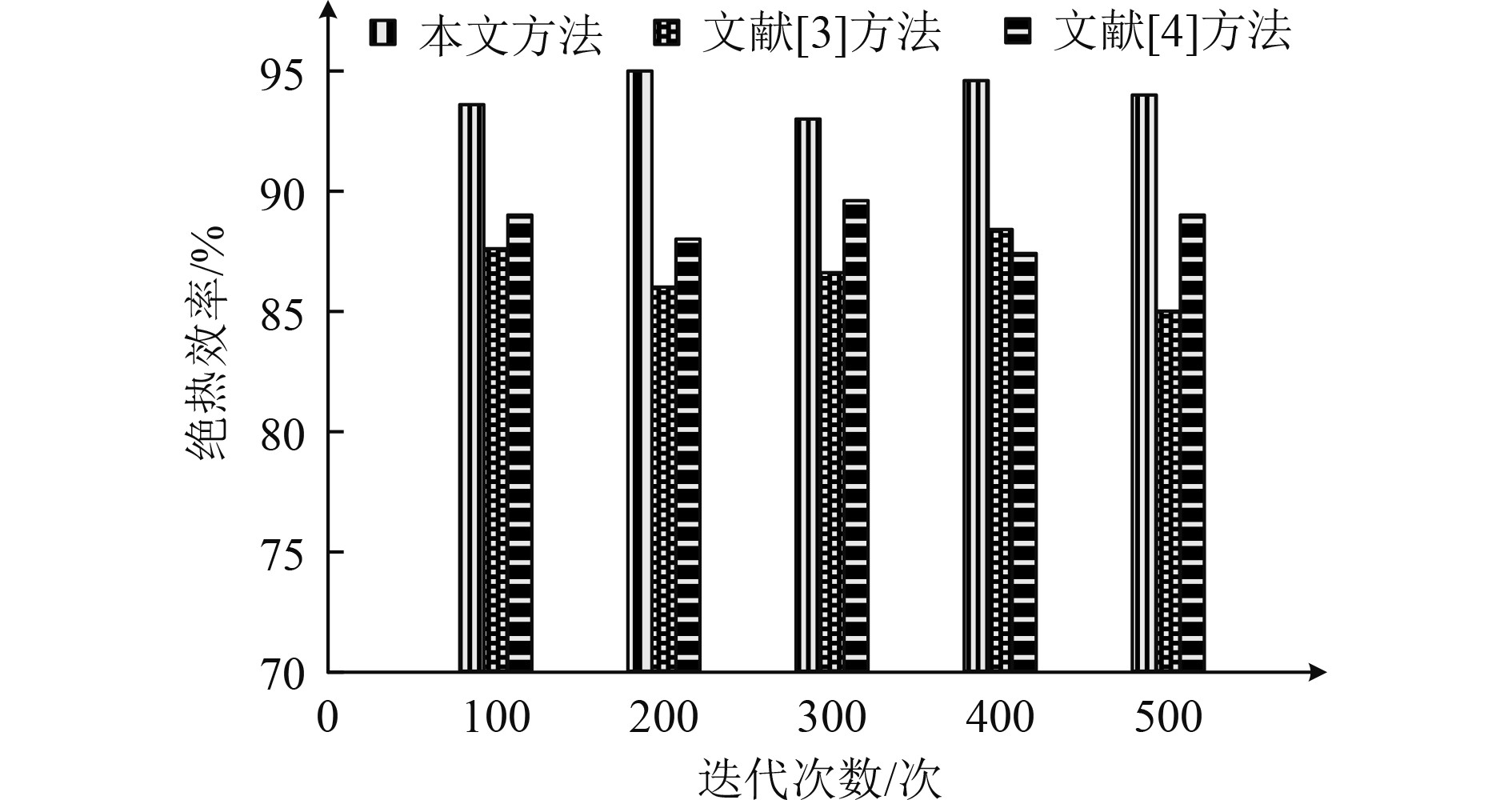
3 实验与分析为了验证舰船大功率轴流压气机智能控制方法的整体有效性,在Matlab平台中对舰船大功率轴流压气机智能控制方法进行测试。设置迭代次数为500次,分别采用本文方法、文献[3]方法和文献[4]方法进行测试,对比不同方法的绝热效率和总压损失系数,测试结果分别如图1和图2所示。
|
图 1 不同方法的绝热效率测试结果 Fig. 1 Test result of adiabatic efficiency by different method |
|
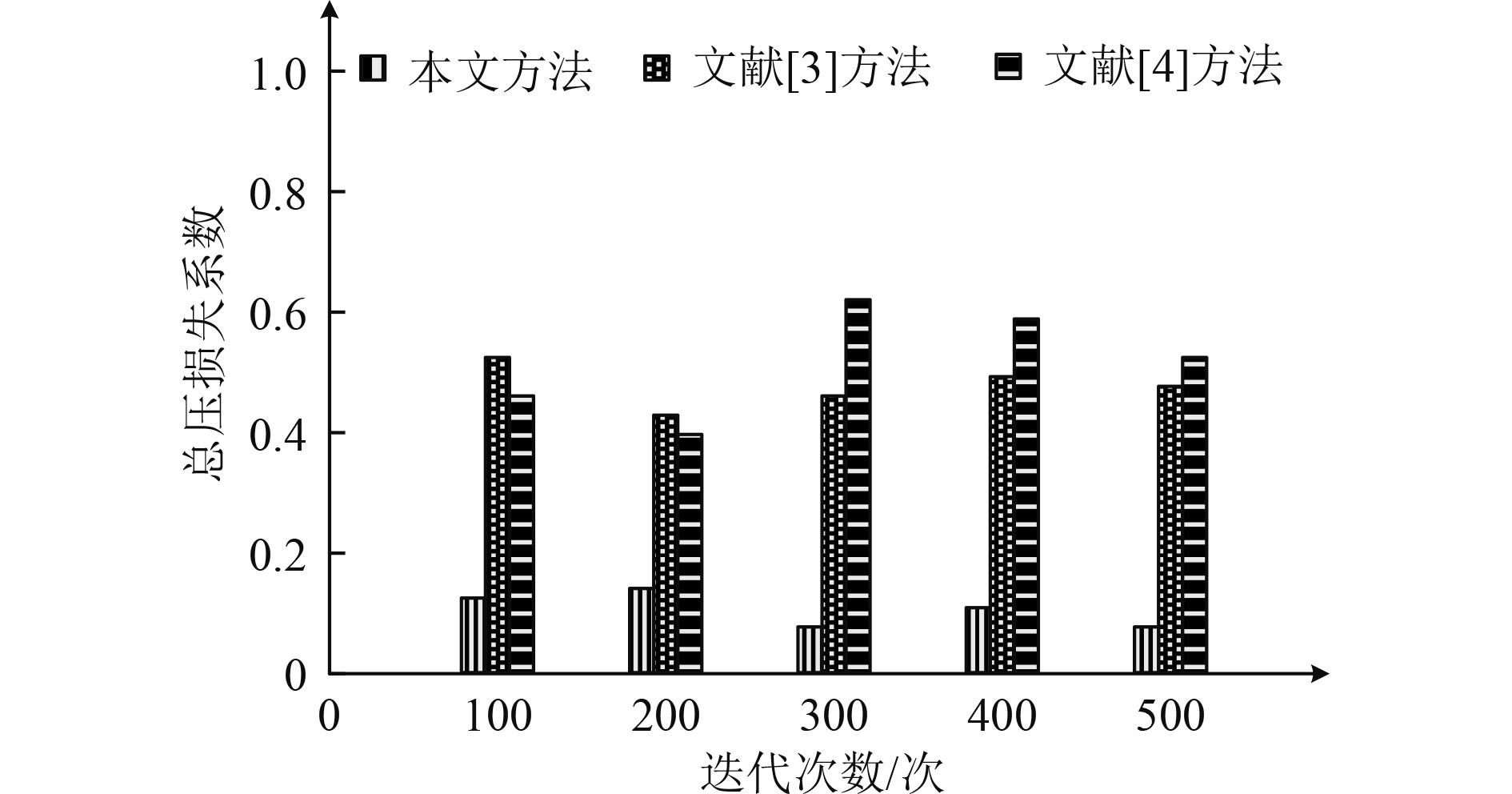
图 2 不同方法的总压损失系数测试结果 Fig. 2 Test result of total pressure loss coefficient by different method |
分析图1的数据可知,本文方法在多次迭代中的绝热效率均在90%以上,文献[3]方法和文献[4]方法在多次迭代中获得的绝热效率均低于90%,对比不同方法的测试结果可知,本文方法的绝热效率较高。
分析图2的数据可知,本文方法在多次迭代中的总压损失系数远远低于文献[3]方法和文献[4]方法的总压损失系数。因为本文方法在舰船大功率轴流压气机控制方程和湍流模型的基础上进行数值模拟,建立舰船大功率轴流压气机优化控制目标函数,在优化控制过程中减小叶片表面浮层的分离区,对流畅通道内的流动结构进行了优化,降低了流动损失,提高了舰船大功率轴流压气机的绝热效率。
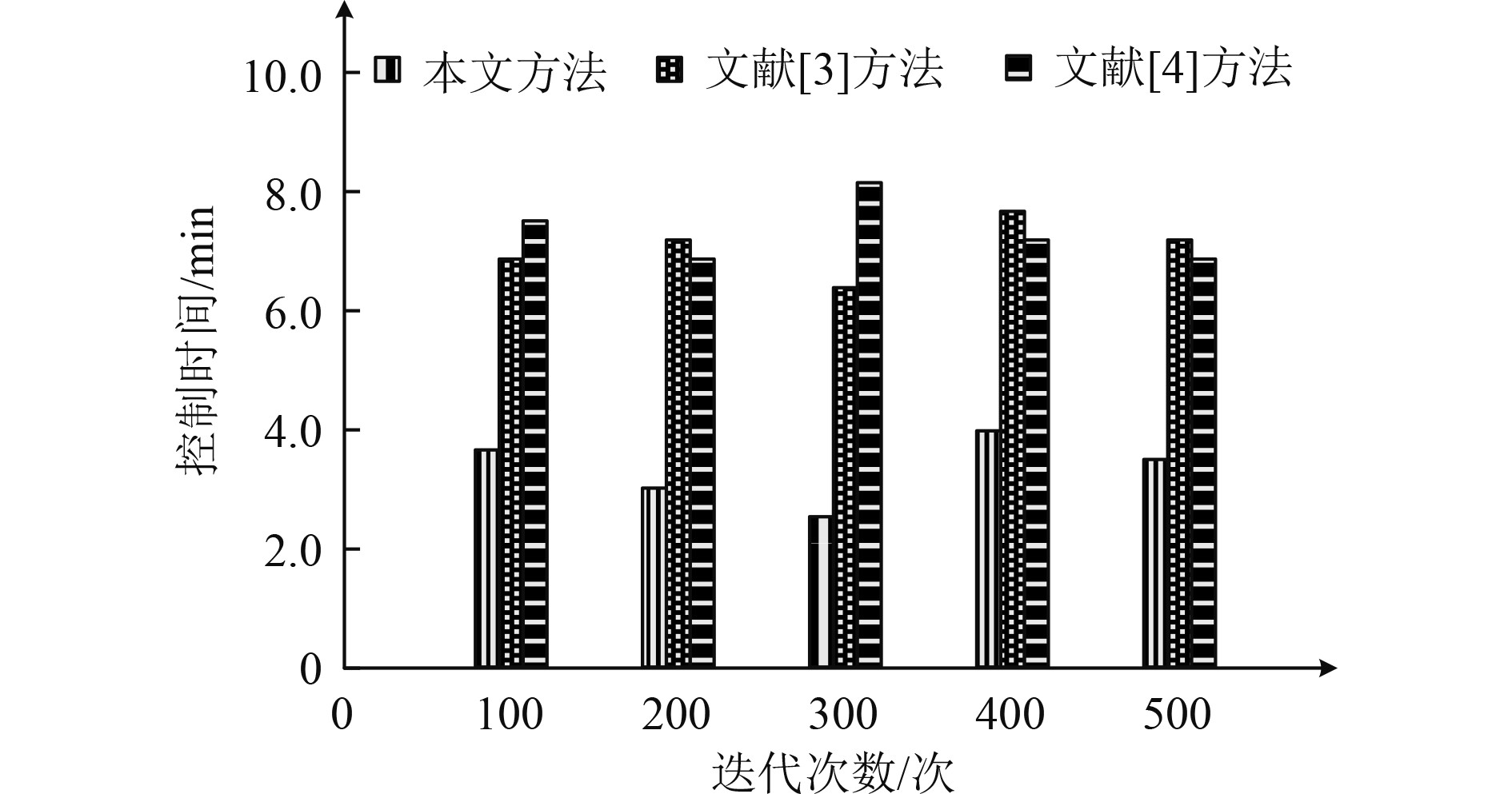
通过测试本文方法、文献[3]方法和文献[4]方法的控制时间测试结果如图3所示。
|
图 3 不同方法的控制时间测试结果 Fig. 3 Test result of contral time by different method |
由图3可知,采用本文方法对舰船大功率轴流压气机进行控制时所用的时间均低于采用文献[3]方法和文献[4]方法对舰船大功率轴流压气机进行控制所用的时间,因为本文方法在数值模拟过程中通过当地时间步长、隐式残差光顺和多重网格法进行加速收敛处理,缩短了控制所用的时间。
4 结 语在舰船发动机中压气机属于核心部件。对舰船大功率轴流压气机提出了宽广稳定工作范围、高效率、低油耗率、大流量和高推重比的要求,同时机组结构还会对压气机级数产生限制,因此需要对舰船大功率轴流压气机控制方法进行优化和研究。目前压气机控制方法存在绝热效率低、总压损失系数高和控制效率低的问题,提出舰船大功率轴流压气机智能控制方法,通过数值模拟方法构建压气机优化控制目标函数,并采用人工蚁群算法对目标函数进行求解,实现舰船大功率轴流压气机的智能控制,解决了目前方法中存在的问题,为舰船大功率轴流压气机的稳定运行提供了保障。
| [1] |
宁方飞, 李一鸣. 一种压气机叶型的可控环量尾缘造型方法[J]. 航空动力学报, 2019, 34(1): 142-155. |
| [2] |
杨承, 黄曼曼, 王平, 等. 压气机抽气储能改进燃气轮机能源系统灵活性分析[J]. 中国电机工程学报, 2018, 38(18): 5510-5517. |
| [3] |
郭倩楠, 李绍斌, 宋西镇, 等. 基于动态边界的跨声速压气机过渡态三维模拟方法[J]. 推进技术, 2019, 40(6): 1231-1238. |
| [4] |
王忠义, 曲锋, 万雷, 等. 基于弯掠参数控制的压气机动叶优化设计[J]. 大连海事大学学报, 2018, 44(1): 99-106. |
| [5] |
杜娟, 张千丰, 王偲臣, 等. 斜流压气机轴向缝机匣处理设计及扩稳机理研究[J]. 工程热物理学报, 2019, 40(4): 751-758. |
| [6] |
田志涛, 郑群, 姜斌, 等. 氦压气机转子叶顶间隙结构研究[J]. 哈尔滨工程大学学报, 2019, 40(5): 938-943. |
| [7] |
陈沁青, 倪计民, 王琦玮, 等. 基于DoE的涡轮增压器压气机优化方法的比较[J]. 车用发动机, 2020(3): 36-43. DOI:10.3969/ji.ssn.1001-2222.2020.03.006 |
| [8] |
唐家茂, 宣海军, 彭煜, 等. 单级轴流压气机叶片预置裂纹法包容性试验研究[J]. 燃气涡轮试验与研究, 2018, 31(1): 18-23. DOI:10.3969/j.issn.1672-2620.2018.01.004 |
| [9] |
韩瑞雪, 陈榴, 段浩杰, 等. 轴流压气机叶型的类/形函数表示方法及气动优化[J]. 热能动力工程, 2020, 35(3): 68-77. |
| [10] |
王爽, 刘永葆, 贺星, 等. 叶顶间隙对跨音速离心压气机气动性能影响分析[J]. 汽轮机技术, 2020, 62(1): 19-22. |
| [11] |
张晓阳, 陈镟宇, 李良才, 等. 斜流轴流组合式多级压气机气动设计与流场数值模拟[J]. 中国舰船研究, 2018, 13(4): 106-112+128. |
| [12] |
张洪鑫, 陈绍文, 王松涛, 等. 定常抽吸与非定常脉动抽吸对高负荷压气机叶栅性能的影响[J]. 大连海事大学学报, 2018, 44(4): 95-101. |
| [13] |
刘家璇, 杨福胜, 邓建强, 等. 组合机匣处理对跨音压气机流动特性的影响[J]. 西安交通大学学报, 2020, 54(4): 173-178. |
| [14] |
任保亮, 杨金广, 刘艳. 基于流线曲率法的轴流及离心压气机通流特性预测[J]. 工程热物理学报, 2020, 41(5): 76-85. |
| [15] |
孟庆鹤, 陈绍文, 刘宏言, 等. 扫频式射流对设计工况压气机叶栅流动分离影响的数值研究[J]. 推进技术, 2020, 41(3): 91-98. |
 2022, Vol. 44
2022, Vol. 44
