0 引　言

舰船综合电力系统具备统一管理舰船能源的优势，其内部电子器件的物理特性^[1-3]，导致综合电力系统会出现暂态失稳情况，降低舰船运行的可靠性^[4]，为此及时控制综合电力系统暂态稳定性，可确保舰船运行的安全可靠性^[5]，在舰船运行中具有较高的价值与意义。汪慧玲^[6]依据非线性控制理论，设计舰船电力系统自适应控制技术，有效自适应控制电力系统，为完善舰船电力系统的工作提供帮助，该技术虽可降低干扰对控制效果的影响，但电力系统自适应控制稳定性较差。迟福建等^[7]利用非线性坐标变换法塑造舰船电力系统非线性等价系统模型，通过自适应估计方法，建立Lyapunov函数，依据该函数实现等价系统模型的稳定控制，该技术可有效控制舰船电力系统，确保电力系统的额定电压不会出现偏差，但该技术建立Lyapunov函数的基础为电力系统必须为可转换成反对称结构的广义系统，但将电力系统转换成广义系统的难度较高，延长控制时间。模糊自适应控制方法，在非线性电力系统不可测问题中，具有较优的鲁棒性，且控制精度高、速度快。为此研究舰船综合电力系统暂态稳定性自适应控制技术，提升自适应控制效果，确保舰船综合电力系统稳定运行。

1 基于反馈模糊控制器的舰船综合电力系统暂态稳定性自适应控制技术 1.1 舰船综合电力系统暂态稳定性数学模型

舰船的运行环境为海上，因此，其电力系统基本属于一个封闭系统，在设计舰船综合电力系统暂态稳定性自适应控制技术时，可将系统内的一台发电机和其余发电机实施等效处理^[8]。本文考虑的情况为2个发电机并联，由于多机系统可等效两机并联系统，因此，设计两机并联系统的自适应控制技术也可控制多机系统。因为舰船电力系统内输电线路短、线路电阻小^[9-11]，所以在舰船综合电力系统暂态稳定性自适应控制技术中无需考虑这两方面的因素。

考虑存在励磁控制的舰船综合电力系统的数学模型如下：

$ \left\{ \begin{gathered} \delta ' = \omega - {\omega _0}，\hfill \\ \begin{aligned}\omega ' = & - \frac{1}{{2M}}\left( {D\omega - D{\omega _0} + \frac{\sin ( \delta ){\omega _0}U_q^l}{x_{d\sum }^l} + {\omega _0}{P_m} - {\omega _0}{P_\tau }} \right) + \\&\frac{{x_q}\sin ( \delta )}{{x_{q\sum }}x_{d\sum }^l} - \frac{x_d^l\sin ( \delta )}{{x_{q\sum }}x_{d\sum }^l} + {d_1}，\end{aligned}\hfill \\ U'^l_q = - \frac{x_{d\sum }U_q^l}{T_{d0}^lx_{d\sum }^l} + \frac{\cos ( \delta )x_d - \cos ( \delta )x_q^l}{T_{d0}^lx_{d\sum }^l} +\frac{{U_{ds}}}{T_{d0}^l} + \frac{u_f}{T_{d0}^l} + {d_2} 。\hfill \\ \end{gathered} \right. $

(1)

其中：舰船综合电力系统内发电机功角为δ、转速为ω；发电机暂态电抗后其内部电势为 $ U_q^l $ ；阻尼系数为D；发电机正常运行情况下的磁场电压是 $ {U_{ds}} $ ；发电机励磁绕组开路时间是 $ T_{d0}^l $ ；舰船综合电力系统同步转速为 $ {\omega _0} $ ；发电机转动惯量为M；发电机d和q轴暂态电抗为 $ x_{d\Sigma }^l $ 和 $ {x_{q\Sigma }} $ ；发电机输入和输出电磁功率为 $ {P_m} $ 和 $ {P_\tau } $ ；作用于发电机转子中的有界扭矩干扰与定子电磁暂态干扰为 $ {d_1} $ 和 $ {d_2} $ 。

根据式（1）可知，影响舰船综合电力系统暂态稳定性的主要参数为δ，ω， $ U_q^l $ ， $ {U_{fds}} $ ， $ {P_\tau } $ 。

为便于自适应控制器的设计，令 $H\left( x \right) = \left\{ \delta ',\right. \left.\omega ',U'^l_q \right\} = {\left[ {{h_1}\left( x \right), \cdots ,{h_n}\left( x \right)} \right]^{\rm{T}}}$ ， $x = {\left[ {\delta \mathop {}\nolimits_{} \omega \mathop {}\nolimits_{} U_q^l\mathop {}\nolimits_{} {U_{ds}}\mathop {}\nolimits_{} {P_\tau }} \right]^{\rm{T}}}$ ，因此，引入自适应控制技术后，式（1）的数学模型可简写为：

$ \left\{ \begin{gathered} \dot x = {\boldsymbol{A}}x + {\boldsymbol{B}}\left[ {H\left( x \right) + \left( {\omega ' + U'^l_q} \right)u} \right] ，\hfill \\ y = {\boldsymbol{C}}x 。\hfill \\ \end{gathered} \right. $

(2)

式中： ${\boldsymbol{A}} = \left[ \begin{gathered} 0\;\;1 \hfill \\ 0\;\;0 \hfill \\ \end{gathered} \right]$ ； ${\boldsymbol{B}} = {\left[ {0\mathop {}\nolimits_{} 1} \right]^{\rm{T}}}$ ； ${\boldsymbol{C}} = {\left[ {1\mathop {}\nolimits_{} 0} \right]^{\rm{T}}}$ ；反馈模糊自适应控制器为r；已知舰船综合电力系统输出暂态稳定性自适应控制参考向量为y；舰船综合电力系统状态参考向量为 $ \dot x $ 。

1.2 舰船综合电力系统暂态稳定性反馈模糊控制器设计

通过自适应模糊方法设计舰船综合电力系统暂态稳定性反馈自适应模糊控制器， $ {h_i}\left( {x\left| {{\theta _i}} \right.} \right) $ 代表舰船综合电力系统暂态稳定性自适应控制目标，在线调整的舰船综合电力系统暂态稳定性影响参数的向量矩阵为 $ {\theta _i} $ ， $ i \in n $ ， $ {h_i}\left( {x\left| {{\theta _i}} \right.} \right) $ 的模糊规则 $ R_i^{} $ 如下：

若 $ {x_j} $ 为 $ {O_{ij}} $ ，那么 $ {\tilde h_i}\left( {x\left| {{\theta _i}} \right.} \right) $ 为 $ G_i^{} $ ，其中 $ {x_j} $ 的隶属度函数和模糊集合为 $ {\psi _{O_{ij}^{}}} $ 和 $ O_{ij}^{} $ 。

设 $ {h_i}\left( {x\left| {{\theta _i}} \right.} \right) $ 的模糊规则为 $ R_i^{} $ ， $ {h_i}\left( {x\left| {{\theta _i}} \right.} \right) $ 的模糊集合为 $ G_i^{} = {\tilde h_i}\left( {x\left| {{\theta _i}} \right.} \right) $ ；通过乘积推理与中心平均解模糊器^[12]，设计舰船综合电力系统暂态稳定性自适应控制目标的模糊系统，公式如下：

$ {\tilde h_i}\left( {x\left| {{\theta _i}} \right.} \right) = \frac{{\displaystyle\sum\limits_{\lambda = 1}^{{m^2}} {{\theta _{i\lambda }}{\rho _i}\left( x \right)} }}{{\displaystyle\sum\limits_{\lambda = 1}^{{m^2}} {{\rho _i}\left( x \right)} }}。$

(3)

其中：模糊基函数为 ${\rho _{ij}}\left( x \right) = \frac{{\displaystyle\prod\limits_{j = 1}^{2n} {{\psi _{{O_{ij}}}}\left( {{x_j}} \right)} }}{{\displaystyle\sum\limits_{j = 1}^{2n} {\displaystyle\prod\limits_{j = 1}^{2n} {{\psi _{{O_{ij}}}}\left( {{x_j}} \right)} } }}$ ；模糊规则数量为 $ {m^2} $ ， $ \lambda \in {m^2} $ 。

令 $\tilde H\left( {x\left| \varphi \right.} \right) = {\left[ {{{\tilde h}_1}\left( {x\left| {{\theta _i}} \right.} \right), \cdots ,{{\tilde h}_n}\left( {x\left| {{\theta _n}} \right.} \right)} \right]^{\rm{T}}} = {\varphi ^{\rm{T}}}\rho \left( x \right)$ ， $\varphi = {\rm{diag}}\left[ {\theta _1^{\rm{T}}, \cdots ,\theta _n^{\rm{T}}} \right]$ ；建立舰船综合电力系统暂态稳定性控制目标的模糊自适应观测器，公式如下：

$ \left\{ \begin{gathered} \tilde {\dot {x}} = {\boldsymbol{A}}\tilde x + {\boldsymbol{B}}\left[ {\tilde H\left( {\tilde {x}\left| \varphi \right.} \right) + \left( {\omega ' + U'^l_q} \right)r - {r_a} - {r_s}} \right] + {{\boldsymbol{K}}_0}\left( {y - C\tilde x} \right)，\hfill \\ \tilde {y} = {\boldsymbol{C}}\tilde {x}。\hfill \\ \end{gathered} \right. $

(4)

其中： $ \dot x $ ，y与x估计向量为 $\tilde {\dot {x}}$ ， $ \tilde y $ ， $ \tilde x $ ；观测增益矩阵为 ${{\boldsymbol{K}}_0}$ ；自适应控制辅助补偿项为 $ {r_a} $ 和 $ {r_s} $ 。

令暂态稳定性自适应控制目标的观测误差为 $\hat E = x - \tilde x$ ， $ \hat e = y - \tilde y $ ，那么：

$ \left\{ \begin{gathered} \dot {\hat {E}} = {\boldsymbol{A}}\hat {E} - {{\boldsymbol{K}}_0}{C^{\rm{T}}}\hat {E} + {\boldsymbol{B}}H\left( x \right) - {\boldsymbol{B}}\tilde {H}\left( {\tilde {x}\left| \varphi \right.} \right) + {\boldsymbol{B}}{r_a} + {\boldsymbol{B}}{r_s} ，\hfill \\ e = {\boldsymbol{C}}\hat {E} ，\hfill \\ \end{gathered} \right. $

(5)

$ {\varphi ^*} $ 的最佳参数估计值如下：

$ {\varphi ^*} = \mathop {\arg \min }\limits_{\varphi \in \Omega } \left[ {\sup \left\| {\tilde H\left( {\tilde x\left| \varphi \right.} \right) - H\left( x \right)} \right\|} \right]，$

(6)

其中，已知的舰船综合电力系统暂态稳定性影响参数向量矩阵的有界闭子集为 ${\boldsymbol{\varOmega}}$ 。

暂态稳定自适应控制的模糊最小逼近误差如下：

$ w = \left[ {H\left( x \right) - \tilde H\left( {\tilde x\left| {{\varphi ^*}} \right.} \right)} \right]，$

(7)

根据式（7）和式（5）可得：

$ \dot {\hat {E}} = {\boldsymbol{A}}\hat {E} - {{\boldsymbol{K}}_0}{\boldsymbol{C}}\hat {E} + {\boldsymbol{B}}\left[ {{{\bar {\Theta} }^{\rm{T}}}\rho \left( x \right) + w + {r_a} + {r_s}} \right] ，$

(8)

其中， $ \bar \Theta = {\Theta ^*} - \Theta $ 。

令w为有界的，即 $ \left\| w \right\| \leqslant S $ ，则反馈自适应模糊控制器的表达式如下：

$ \left\{ \begin{gathered} r = \frac{{\left[ { - \tilde {H}\left( {\tilde {x}\left| \rho \right.} \right) + {y^2} + K_C^{\rm{T}}\left( {\tilde {\dot {x}} - \tilde {x}} \right) + {r_a} + {r_s}} \right]}}{{\left( {\omega ' + U'^l_q} \right)}}，\hfill \\ {r_a} = K_0^{\rm{T}}{P_1}\left( {\tilde {\dot {x}} - \tilde {x}} \right)，\hfill \\ {r_s} = - {{\rm{sgn}}} \left( {{e^{\rm{T}}}{P_2}B} \right) 。\hfill \\ \end{gathered} \right. $

(9)

其中，暂态稳定性自适应控制目标的正定矩阵为 ${{\boldsymbol{P}}_1}$ 和 ${{\boldsymbol{P}}_2}$ 。

在式（4）内添加式（9）并结合式（8）得：

$ \dot {\hat E} = \left( {{\boldsymbol{A}} - {\boldsymbol{B}}{K_C}} \right)\left( {\tilde {\dot x} - \tilde x} \right) - {{\boldsymbol{K}}_0}{{\boldsymbol{C}}^{\rm{T}}}\hat E，$

(10)

根据式（9）可获取舰船综合电力系统暂态稳定性控制参数向量的自适应律如下：

$ \dot \varphi = \gamma \rho \left( {\tilde x} \right){B^{\rm{T}}}{{\boldsymbol{P}}_2}\dot {\hat E} = \gamma \rho \left( {\tilde x} \right)\hat e。$

(11)

其中，γ为设计参数，在 $ \dot \varphi > 0 $ 情况下，说明舰船综合电力系统暂态稳定性自适应模糊控制技术可确保整个舰船封闭系统达到暂态稳定，完成自适应控制，同时 $ \mathop {\lim e}\limits_{t \to \infty } = \mathop {\lim \tilde e}\limits_{t \to \infty } = 0 $ 。

1.3 基于改进蝙蝠算法的自适应控制模糊规则优化

利用改进蝙蝠算法优化舰船综合电力系统暂态稳定性反馈模糊自适应控制器的模糊规则，令各模糊规则均代表1只蝙蝠个体，具体步骤如下：

步骤1　设置优化反馈模糊自适应控制器模糊规则的蝙蝠种群数量m，蝙蝠接近最佳模糊规则时的响度 $ {A_{i'}} $ ，蝙蝠接近最佳模糊规则时的脉冲发射率 $ {r_{i'}} $ ^[13]，蝙蝠搜索反馈自适应模糊控制器模糊规则时的频率 $ {Q_{\min }}\sim{Q_{\max }} $ ，迭代次数N，模糊规则空间维数b。

步骤2　初始化Q，蝙蝠速度矩阵v，随机初始化编码各蝙蝠个体，即编码模糊规则，求解模糊规则的适应度 $f'\left( {{\textit{z}_{i'}}} \right)$ ，获取目前最佳个体位置 ${\textit{z}_{{\rm{best}}}}$ ，存储 ${\textit{z}_{{\rm{best}}}}$ 的位置信息。

步骤3　更新 $ {v_{i'}} $ 与 $\textit{z}_{i'}^t$ ，更新公式如下：

$ \left\{ \begin{gathered} v_{i'}^t = v_{i'}^{t - 1} + \left( {\textit{z}_{i'}^t - {\textit{z}_*}} \right)\left( {{Q_{\min }} + \varpi {Q_{\max }} - \varpi {Q_{\min }}} \right)，\hfill \\ \textit{z}_{i'}^t = \textit{z}_{i'}^{t - 1} + bv_{i'}^t ，\hfill \\ \end{gathered} \right. $

(12)

其中，随机变量是 $ {h_{\min }} $ 。

蝙蝠局部搜索舰船综合电力系统暂态稳定性反馈自适应模糊控制器模糊规则过程中， ${z_{{\rm{new}}}}$ 的更新公式如下：

$ {{z}_{{\rm{new}}}} = {\textit{z}_{{\rm{old}}}} + \eta \mu {A^t}。$

(13)

其中：当前最佳解是 ${\textit{z}_{{\rm{old}}}}$ ；新解是 ${\textit{z}_{{\rm{new}}}}$ ；随机数是 $\eta \in \left[ { - 1,1} \right]$ ；A的衰减系数是μ。

步骤4　通过离散修正算子调整 $\textit{z}_{i'}^t$ ，对蝙蝠算法进行改进，提升模糊规则优化精度，并求解位置调整后模糊规则的适应度 $f'\left( {{\textit{z}_{i'}}} \right)$ ，离散修正算子符合离散化舰船综合电力系统暂态稳定性反馈自适应模糊控制器内，与模糊规则语言值不匹配的变量，将其调整至标准区间中，最近似的整数就是计算获取的模糊语言值^[14]，四舍五入计算，调整公式如下：

$ {U'_{i',j'}}\left( {{z_{k'}}} \right) = \left\{ \begin{gathered} {Z_{\min }},Round\left[ {{U_{i',j'}}\left( {{z_{k'}}} \right)} \right] ，\hfill \\ {Z_{\max }},Round\left[ {{U_{i',j'}}\left( {{z_{k'}}} \right)} \right] > {Z_{\max }}。\hfill \\ \end{gathered} \right. $

(14)

其中： $ {Z_{\max }} $ 为调整模糊规则的模糊控制表内搜索点坐标； $ {Z_{\min }} $ 和 $ {Z_{\max }} $ 为模糊语言值上、下界； ${U'_{i',j'}}\left( {{\textit{z}_{k'}}} \right)$ 为调整后模糊规则的模糊控制表内搜索点坐标，即调整后搜索最佳模糊规则蝙蝠的位置。

步骤5　衡量调整后的 $\textit{z}_{i'}^t$ 是否符合变异条件 ${\rm{rand}} > {r_{i'}}$ ，其中 ${\rm{ rand}} \in \left( {0,1} \right)$ ，若符合变异条件，那么更新蝙蝠全局最佳位置 ${\textit{z}_{{\rm{best}}}}$ ，反之，继续步骤6。

步骤6　如果 ${\rm{rand}} > {A_{i'}}$ ，同时 $f'\left( {{\textit{z}_{i'}}} \right) < {f'_{{\rm{new}}}}$ ，那么接收这个新解，更新模糊规则的适应度 $ {f'_{i'}} $ ，提升 $ {r_{i'}} $ ，降低 $ {A_{i'}} $ ，获取最佳舰船综合电力系统暂态稳定性反馈自适应模糊控制器模糊规则，反之，继续步骤7。

步骤7　衡量新位置的 ${f'_{{\rm{new}}}}$ ，比当前最佳的 ${f'_{{\rm{best}}}}$ 更好，如果 ${f'_{{\rm{best}}}} \leqslant {f'_{\rm{{new}}}}$ ，那么更新 ${\textit{z}_{{\rm{best}}}}$ 与 ${f'_{{\rm{best}}}}$ ，获取最佳舰船综合电力系统暂态稳定性反馈模糊自适应控制器的模糊规则，反之，继续步骤8。

步骤8　衡量是否达到 $ {t_{\max }} $ ，如果达到 $ {t_{\max }} $ ，那么终止算法，继续步骤9，反之，返回至步骤3。

步骤9　输出全局最优解，即最佳舰船综合电力系统暂态稳定性反馈模糊自适应控制器的模糊规则。

依据最佳模糊规则控制反馈模糊自适应控制器，提升舰船综合电力系统暂态稳定性自适应控制效果。

2 实验分析

通过Matlab仿真软件，设计两机并联舰船综合电力系统，仿真分析本文技术自适应控制舰船综合电力系统暂态稳定性的效果，仿真舰船综合电力系统的设置参数如表1所示。

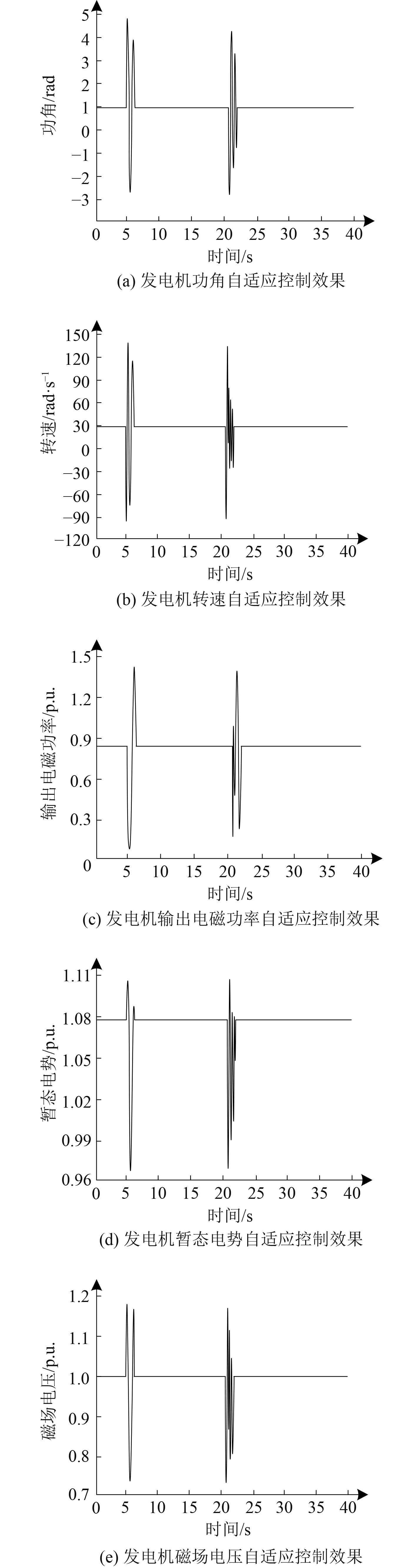
利用Matlab仿真软件设置该舰船综合电力系统在前5 s时运行正常，在5 s时该舰船综合电力系统发电机出现三相短路故障，并在20 s时在该系统内突加5.5 kW的静负载，导致舰船综合电力系统出现暂态失稳情况，利用本文技术自适应控制该舰船综合电力系统暂态稳定性，功角、转速、输出电磁功率、暂态电势与磁场电压的自适应控制效果如图1所示。

分析图1可知，在舰船综合电力系统发电机出现三相短路故障时，可有效自适应控制发电机的功角、转速、输出电磁功率、暂态电势与磁场电压，且自适应控制时间均仅需2 s左右，自适应控制时间较短；当运行时间为20 s时，依旧可以较好地自适应控制突加静负载时的发电机功角与转速等参数，自适应控制时间依旧控制在3 s左右。实验证明：在不同故障情况下，均可有效自适应控制舰船综合电力系统暂态稳定性，自适应控制时间在2～3 s左右，便可令系统各主要参数恢复稳定，确保舰船综合电力系统暂态稳定，保证舰船综合电力系统稳定运行。

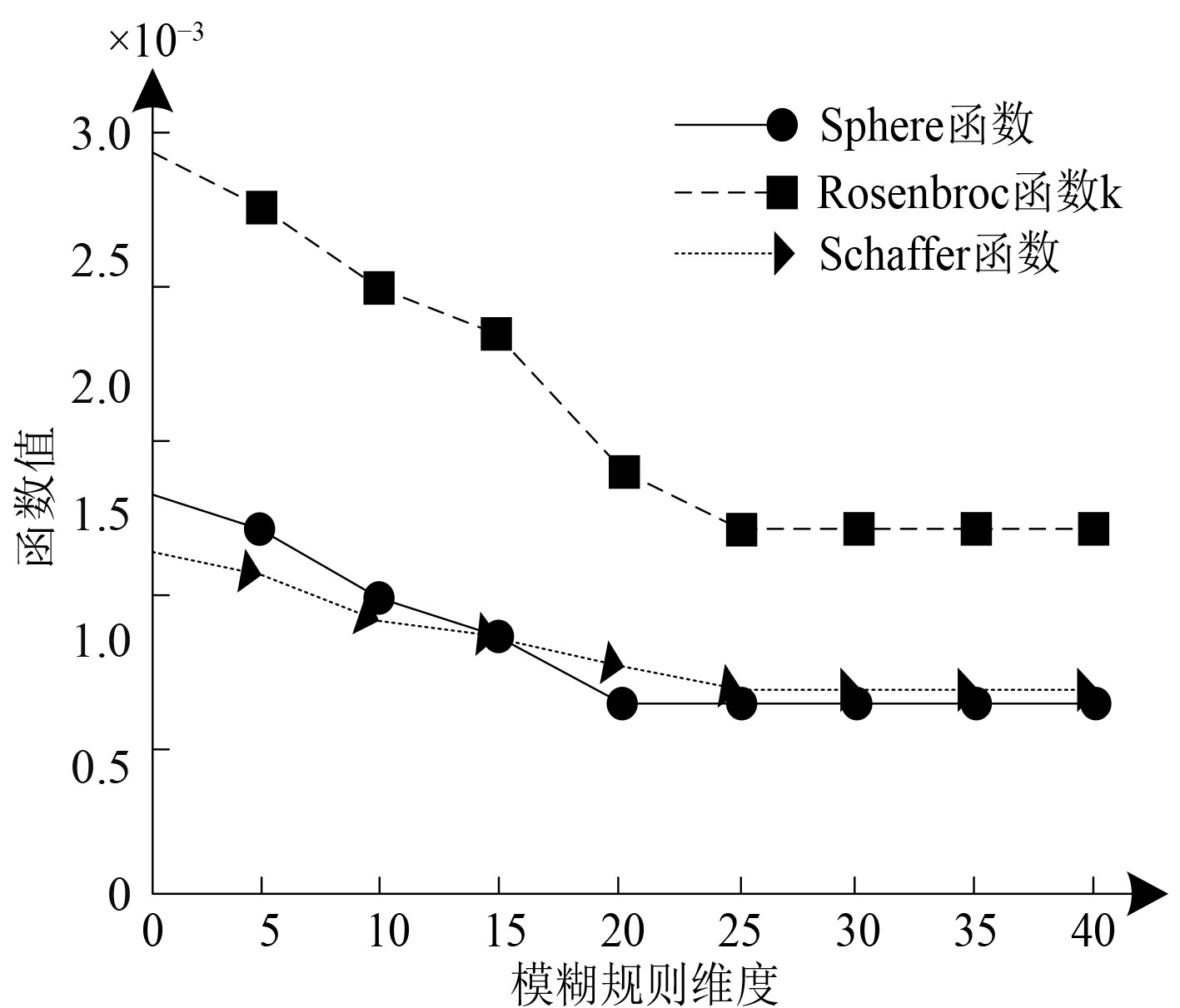
利用改进蝙蝠算法优化反馈自适应模糊控制器的模糊规则，提升舰船综合电力系统暂态稳定性控制效果。为测试模糊规则的优化效果，在Benchmarks测试函数集内，随机选择Sphere函数、Rosenbrock函数与Schaffer函数3个常用函数展开测试，分别用于测试单峰连续优化效果、收敛速度与全局寻优效果，分析本文技术在优化不同维度模糊规则时的各函数值，各函数值均需超过1.0×10⁻³才可确保模糊规则的优化效果达到最佳，测试结果如图2所示。

分析图2可知，模糊规则维度提升，在优化模糊规则时的各函数值均呈下降趋势，当模糊规则维度达到25时，各函数值均趋于稳定，且均稳定在1.0之上，说明本文技术在优化模糊规则时，具备较优的单峰连续优化效果，收敛速度较快且全局寻优效果较优，即模糊规则优化效果较优。

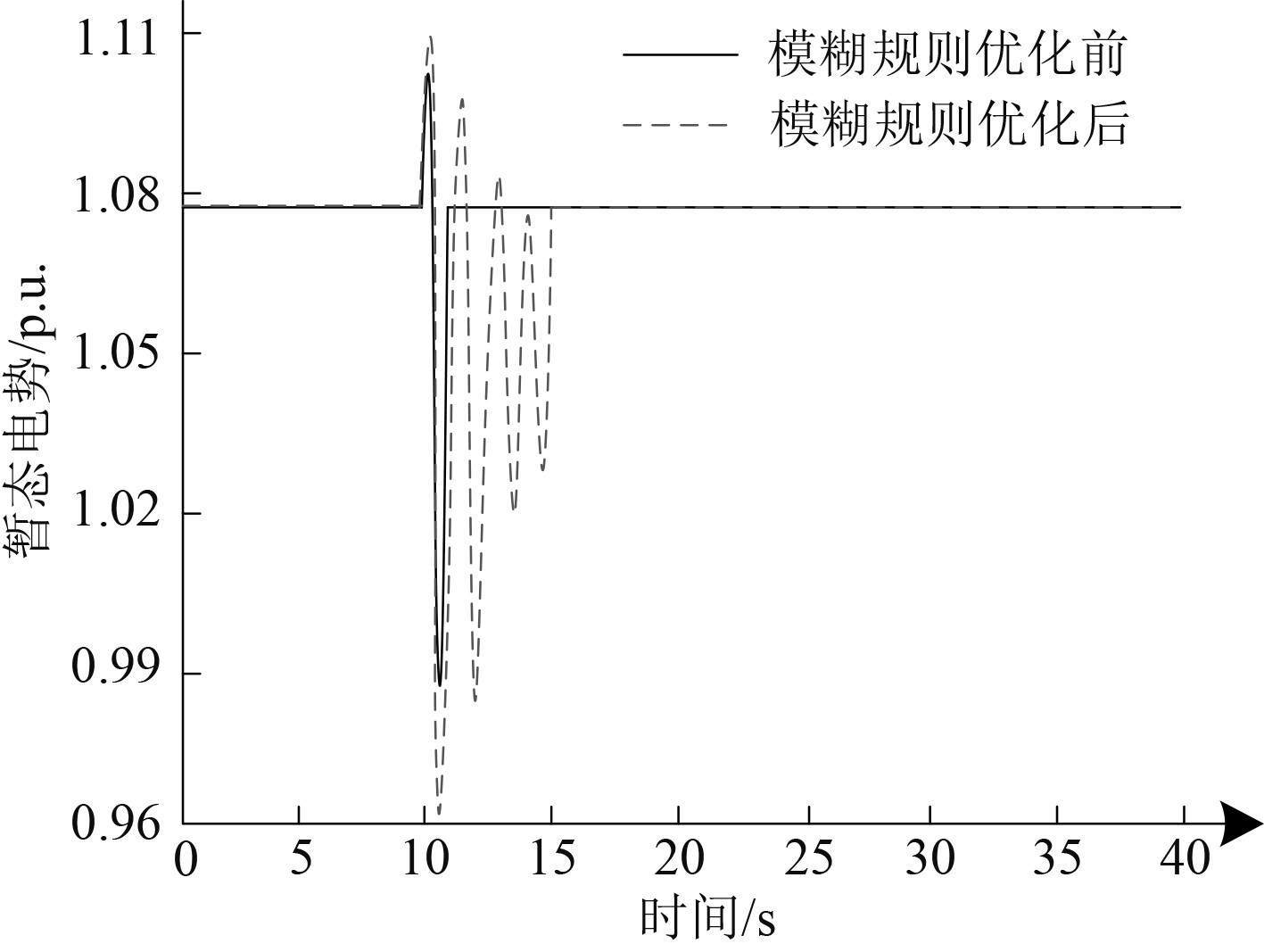
利用Matlab仿真软件分析舰船综合电力系统内添加扰动后，本文技术模糊规则优化前后的暂态稳定性自适应控制效果，舰船综合电力系统正常运行10 s后添加扰动信号，令电力系统呈现暂态失稳状态，以发电机暂态电势为例，自适应控制效果如图3所示。

分析图3可知，优化模糊规则后自适应控制暂态电势的时间明显短于模糊规则优化前，在舰船综合电力系统内添加扰动后，优化模糊规则后可迅速令舰船综合电力系统达到暂态稳定状态，且优化后的超调量明显低于优化前。实验证明本文技术优化模糊规则后可有效缩短自适应控制时间，提升自适应控制效果。

3 结　语

舰船综合电力系统包含平台电力与推进2个系统，综合电力系统的网络结构较为繁琐，经常出现暂态失稳情况，为此研究舰船综合电力系统暂态稳定性自适应控制技术，提升暂态稳定性自适应控制效果。本文以发电机两机并联情况为研究方向，今后还可以深入研究备用发电机和主发电机并联等情况，提升暂态稳定性自适应控制的精度，确保舰船综合电力系统可靠运行。