2. 郑州市轨道交通智能检测重点实验室,河南 郑州 451460
2. Zhengzhou Key Laboratory of Intelligent Detection of Rail Transit, Zhengzhou 451460, China
在船舶电力推进系统发展初期,人们认为使用发电机、变频器等设备代替机械推进系统中的减速器会提高船舶的质量以及体积,并且电力推进系统中存在能量的二次转换,导致效率低、维修费用高,因此初期船舶上很少使用电力推进系统[1]。但是随着以IGBT等功率器件为基础的船舶电力推进技术的迅猛发展,这些技术极大地推动了船舶推进电机系统在机动性、工作效率以及可靠性等性能方面的提升,这使得船舶电力推进技术获得大量的关注,其应用领域不断增大,因此其有着很大的应用前景[2]。船舶电力推进系统随着电力电子技术的发展迈入了一个新的阶段,从一开始的直流推进转变成了交流推进,同时作为一种新的控制方法,直接转矩控制方法使得船舶异步电机的控制变得简洁,提升了船舶异步电机的动态性能,一旦船舶异步电机采用直接转矩的控制方法,则系统中无需实现各种矢量变化,因此极大地简化了船舶异步电机的数学模型,控制系统无需产生PWM信号,而是直接控制,因此在直接控制方法下,船舶异步电机响应快速,极大地体现了直接控制方法的高效性[3]。
1 船舶电力推进系统 1.1 船舶电力推进系统结构船舶电力推进系统主要包括发电、配电、变频驱动、推进器以及控制器等部件[4]。根据船舶推进器的结构进行分类,可以分为轴式、Z型以及吊舱式3种船舶电力推进系统。船舶轴式电力推进系统的结构和传统的内燃机推进式相似,与传统的内燃机推进系统相比,船舶轴式电力推进系统的体积比较小,因此船舶轴式电力推进系统可以安置在船舶的尾部,并且船舶轴式电力推进系统的轴系比传统内燃机推进式系统要短一些;船舶Z型电力推进系统中的螺旋桨安放在船尾水下,并且螺旋桨利用齿轮的传动机制与船尾电力推进系统内的电机相连,在船舶的Z型电力推进系统的控制下,船舶的螺旋桨可以在水下实现360o的旋转,因此船舶在该螺旋桨的控制下可控性得到了增强;船舶吊舱式电力推进系统去除了Z型电力推进系统中的齿轮传动机制,这使得船舶吊舱式电力推进系统的结构简单,提高了传动效率,并且节约了船体内部的空间,这使得船舶在设计生产制造以及使用等方面的灵活性得到了增强[5],因此吊舱式船舶电力推进系统是船舶电力推进系统的重要发展方向[6]。船舶电力推进系统的概念功能结构如图1所示。
|
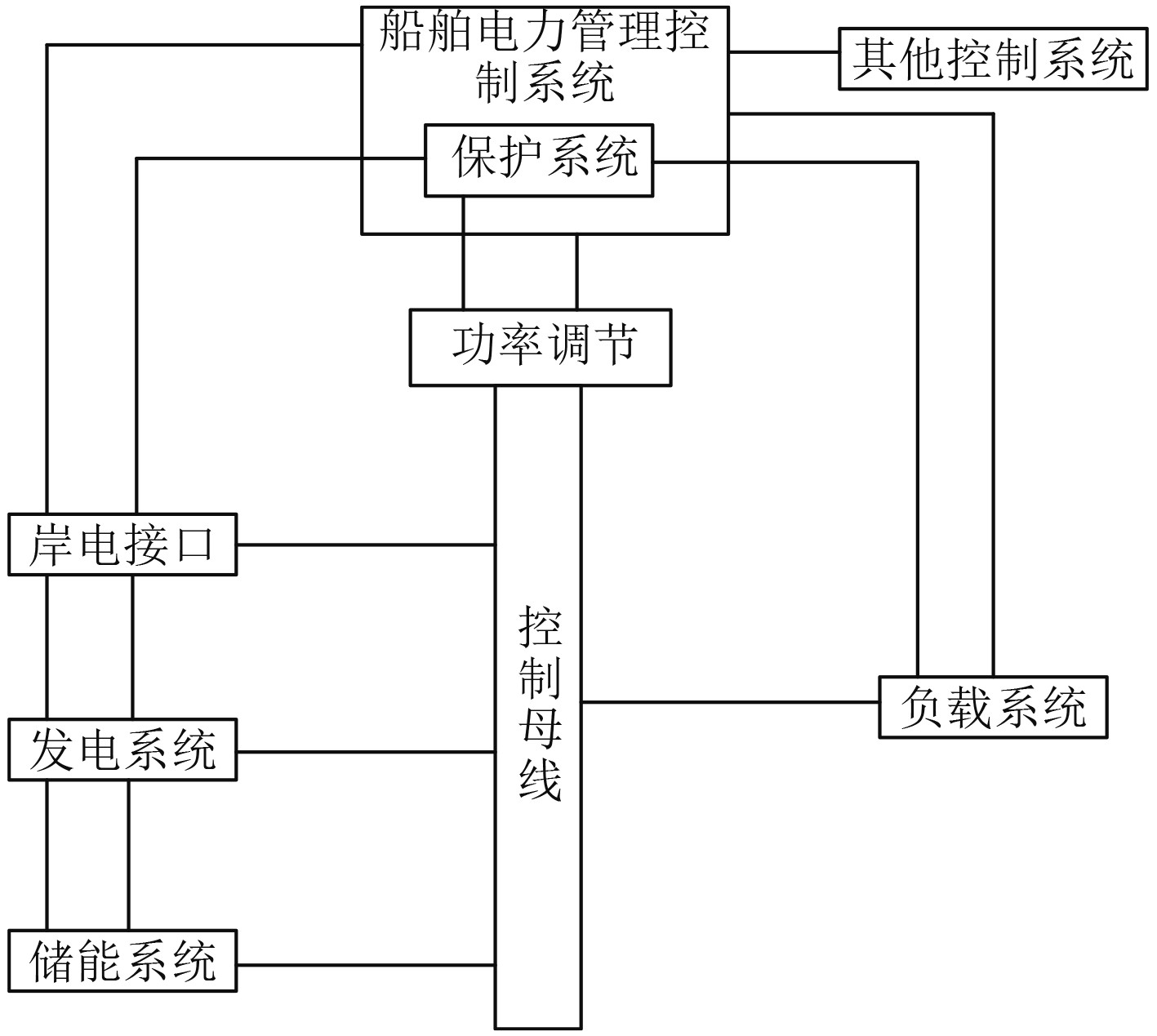
图 1 船舶推进系统结构 Fig. 1 Ship propulsion system structure |
图中,岸电接口的功能是当舰船停靠在码头的时候,通过该接口可以将岸上的供电系统接到船舶上,以降低船舶上能源的使用,岸电接口通常由变压器和整流器共同构成[7]。船舶电力推进系统中的发电系统主要包含原动机、整流设备以及发电机3个部分,通常使用柴油机或者汽轮机作为原动机,汽轮机组通常使用在大容量系统中,在中小容量的系统中一般使用柴油发电机组,整流设备的任务是将系统中发电机输出的交流电转换成直流电,并且将电力集中到主母线上。为了降低发电系统占用的空间,发电模块通常使用带整流器的高速发电机以及同步多相发电机组合的形式[8]。储能系统主要有维护新能源的稳定性以及均衡负载受到的冲击2个功能,超级大电容、蓄电池等为常见的储能设备,通常会使用双向DC/DC变换器以确保储能系统能够很安全地并入船舶电力推进系统[9]。负载系统中主要包含脉冲、推进、服务类以及大功率等负载模块。脉冲负载模块是指EMALS等功率脉冲系统;推进负载模块可以给船舶提供航行的动力,主要包含推进电机以及螺旋桨等设备;服务类负载模块中包含电力系统冷却泵、照明系统以及其他日常生活设备;大功率负载模块是给雷达等十分重要的检测类负载单独提供电力的负载中心。控制母线中主要有断路器、负载开关、终端设备、隔离器件等模块,通过控制母线系统可以对船舶电力推进系统中的各类设备进行通断控制,以保证船舶系统的运行需求[10]。船舶电力管理控制系统中集中了监控、保护以及管理,该系统通过对系统中各类设备的工作状态进行监测,并且根据监测结果对船舶电力推进系统进行调控,使得船舶电力推进系统一直处于高效率的工作状态,一旦整个系统出现故障,则可以对故障做出及时准确的判断,并提出解决措施,实现故障清除,确保船舶电力推进系统的高可靠性以及高稳定性运行,提升船舶的生命力。
1.2 船舶推进系统建模船舶在海面上航行时,螺旋桨在海浪中的运行状态可以分成两部分,一是螺旋桨的桨轴会随着海浪波面的浮沉而变化;二是波浪会影响船舶螺旋桨的进速。
在图2中,x轴和静止的海平面重合,波浪沿着x轴的负方向运动,船舶螺旋桨距离水面深度为hs,该深度会受到垂直震荡幅值以及纵倾角的影响,船舶桨叶以VA的进度向x轴正方向前进。假设海水是无粘性的流体,海水深度无限,则根据波浪理论,可以得到海浪的波面方程,具体为:

|
图 2 波浪中螺旋桨运动模型 Fig. 2 Propeller motion model in waves |
| $ \zeta = a\sin \left( {Kx - \sigma t} \right)\text{。} $ | (1.1) |
船舶的速度势可以表示为:
| $ \varphi = \frac{{ag}}{\sigma }{e^K}\cos \left( {Kx - \sigma t} \right)\text{。} $ | (1.2) |
式中:K为海浪的波数;a为海浪的波幅。波浪下方x方向上的海水质点的运动速度可以表示为:
| $ {v_x} = - a\sigma {e^K}\sin \left( {Kx - \sigma t} \right)\text{。} $ | (1.3) |
船舶螺旋桨桨叶的进度可以表示为:
| $ V_A' = {V_A} - a\sigma {e^K}\sin \left( {Kx - \sigma t} \right)\text{。} $ | (1.4) |
船舶螺旋桨的进度系数可以表示为:
| $ {J_P} = \frac{{V_A'}}{{n{D_P}}}\text{。} $ | (1.5) |
船舶螺旋桨距离海浪波面的深度值可以表示为:
| $ h = {h_s} + \zeta \text{。} $ | (1.6) |
船舶在大海上正常行驶的过程中,通常是正向前进,此时船舶螺旋桨的转速n>0,因此可以构建出船舶螺旋桨的推力以及转矩的数学模型,表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_P} = \left( {1 - {t_p}} \right)T} ,\\ {T = \rho {n^2}D_p^4{K_T}\left( {{J_P},h/D} \right)},\\ {M = \rho {n^2}D_p^5{K_M}\left( {{J_p},h/D} \right)}。\end{array}} \right.\text{} $ | (1.7) |
式中:M为扭矩;Dp为桨叶直径;tp为减额系数;KT(Jp,h/D)为推力因子;KM(Jp,h/D)为转矩因子;考虑船舶在航行过程中的海水伴流现象,船舶螺旋桨的进度系数可以表示为:
| $ {J_p} = \left( {1 - {w_p}} \right){V_A}/n{D_p}\text{。} $ | (1.8) |
其中wp为伴流系数。
当船舶螺旋桨的进度系数Jp从0到0.7的时候,雷诺系数RN可以表示为:
| $ {R_N} = \frac{{{b_{0.75R}}\sqrt {V_A^2 + {{\left( {0.75\text{π} n{D_p}} \right)}^2}} }}{{{v_m}}} \text{。} $ | (1.9) |
式中,vm为粘性系数,通常取1.139×10−6m2/s。
当船舶在航行的过程中遇到较大风浪的时候,受到纵摇以及升沉运动的影响,船舶螺旋桨可能会露在海面之上,则此时负荷会出现短暂的大范围的脉动变化,这时候如果使用转子磁场定向控制技术,则会使得船舶推进系统的输出功率出现很大的波动,最终会损坏船舶的电力系统,为了从一定程度上抑制推进系统输出功率的波动,船舶在大浪中航行的时候通常采用恒功率模式,异步电机的输出功率可以表示为:
| $ {P_{em}} = p\frac{{{L_m}}}{{{L_r}}} \varOmega {\psi _{rd}}{i_{sq}}\text{。} $ | (1.10) |
如果船舶在大浪中航行的时候采用恒功率模式,那么船舶螺旋桨在海浪中的转速会出现较大变化,这会增加损坏船舶螺旋桨的概率,因此需要协调船舶推进电机输出功率与船舶螺旋桨转速之间的关系[11]。船舶在风浪很小的海面上航行,船舶螺旋桨的转速可以控制得比较好,但是在海面波浪较大的时候,要尽可能地避免推进电机的输出功率出现很大的波动,因为较大的功率波动意味着在消耗不必要燃料的同时扩大了船舶电网的谐波,会使得船舶出现断电等现象,因此船舶推进电机的输出功率需要满足下式:
| $ {P_m} = 2\text{ π} nM = 2\text{ π} {K_M}\rho {D^5}{n^3}\text{。} $ | (1.11) |
由式(10)可以得到船舶推进电机的输出功率和螺旋桨转速之间的关系如下:
| $ n = \sqrt[3]{{\frac{{{P_m}}}{{2\text{ π} {{{K}}_M}\rho {D^5}}}}}\text{。} $ | (1.12) |
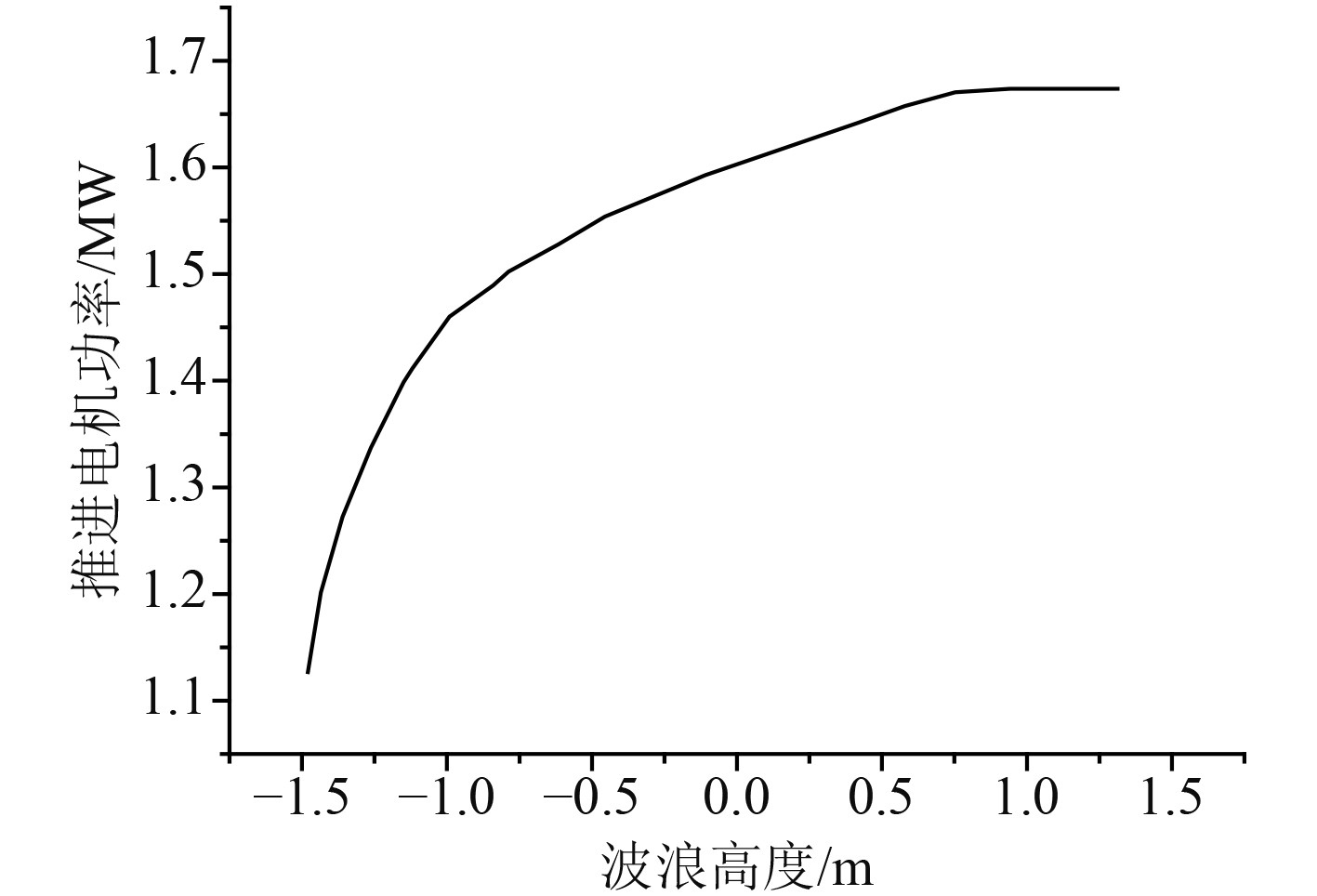
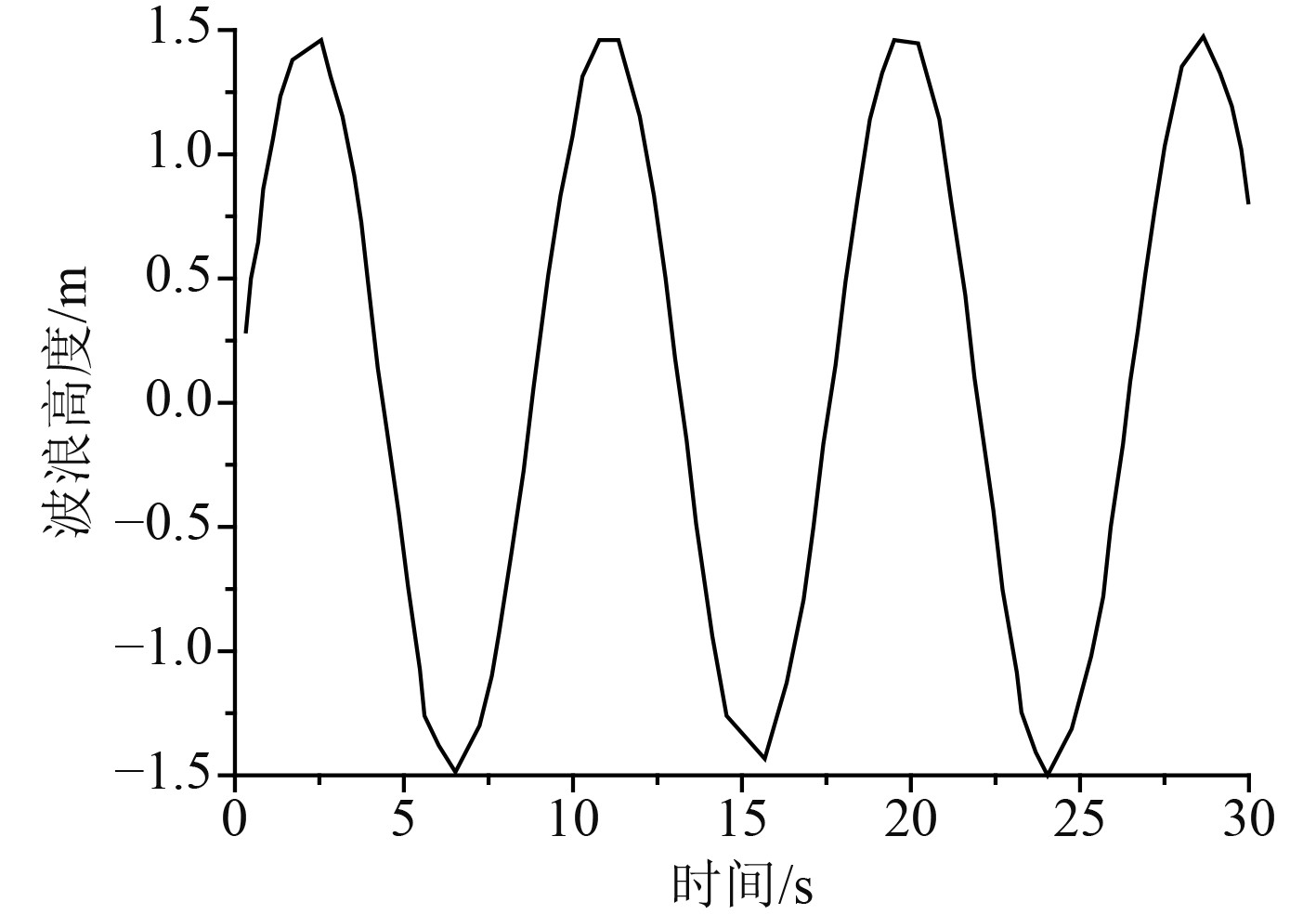
船舶推进电机输出功率和海浪的高度之间的关系如图3所示,波浪高度随时间变化如图4所示。
|
图 3 船舶推进电机输出功率和海浪高度之间的关系 Fig. 3 Relationship between output power of marine propulsion motor and sea wave height |
|
图 4 海面波浪高度 Fig. 4 Sea wave height |
由于船舶异步电机工作系统存在多变量以及非线性等特征,这使得船舶异步电机的数学模型也表现出高阶、强耦合以及非线性等动态特征[12]。因此构建出精确的异步电机的数学模型对提升异步电机的研究深度有很大的帮助。考虑到船舶异步电机工作系统的非线性、多变量等性质,在构建异步电机动态模型的时候,为了更加方便地理解异步电机的工作原理,则不考虑异步电机的空间谐波、铁芯的磨损以及磁路饱和等问题,并且忽略异步电机绕组电阻受到频率以及绕组变化的影响,则异步电机定子绕组的电压方程可以表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{u_A} = {i_A}{R_s} + \dfrac{{{\rm{d}}{\psi _A}}}{{{\rm{d}}t}}} ,\\ {{u_B} = {i_B}{R_s} + \dfrac{{{\rm{d}}{\psi _B}}}{{{\rm{d}}t}}},\\ {{u_C} = {i_C}{R_s} + \dfrac{{{\rm{d}}{\psi _C}}}{{{\rm{d}}t}}} 。\end{array}} \right.\text{} $ | (2.1) |
式中:uA,uB,uC为定子相电压;iA,iB,iC为定子相电流;ψA,ψB,ψC为定子绕组磁链;Rs为定子电阻。异步电机转子绕组的电压方程为:
| $ \left\{ {\begin{array}{*{20}{l}} &{{u_a} = {i_a}{R_r} + \dfrac{{{\rm{d}}{\psi _a}}}{{{\rm{d}}t}}},\\ &{{u_b} = {i_b}{R_r} + \dfrac{{{\rm{d}}{\psi _b}}}{{{\rm{d}}t}}},\\ &{{u_c} = {i_c}{R_r} + \dfrac{{{\rm{d}}{\psi _C}}}{{{\rm{d}}t}}}。\end{array}} \right.\text{} $ | (2.2) |
式中,ua,ub,uc为转子相电压;ia,ib,ic为转子相电流;ψa,ψb,ψc为转子绕组磁链;Rr为转子电阻。式(13)和式(14)可以统一写成式(15)的形式。
| $ u = Ri + P\psi \text{。} $ | (2.3) |
忽略粘性摩擦以及扭矩弹性对船舶异步电机的影响,船舶异步电机的转矩方程为:
| $ {T_e} = {T_l} + \frac{J}{{{n_p}}}\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}\text{。} $ | (2.4) |
式中:Tl为转矩值,J为惯量值,ω为角频率。
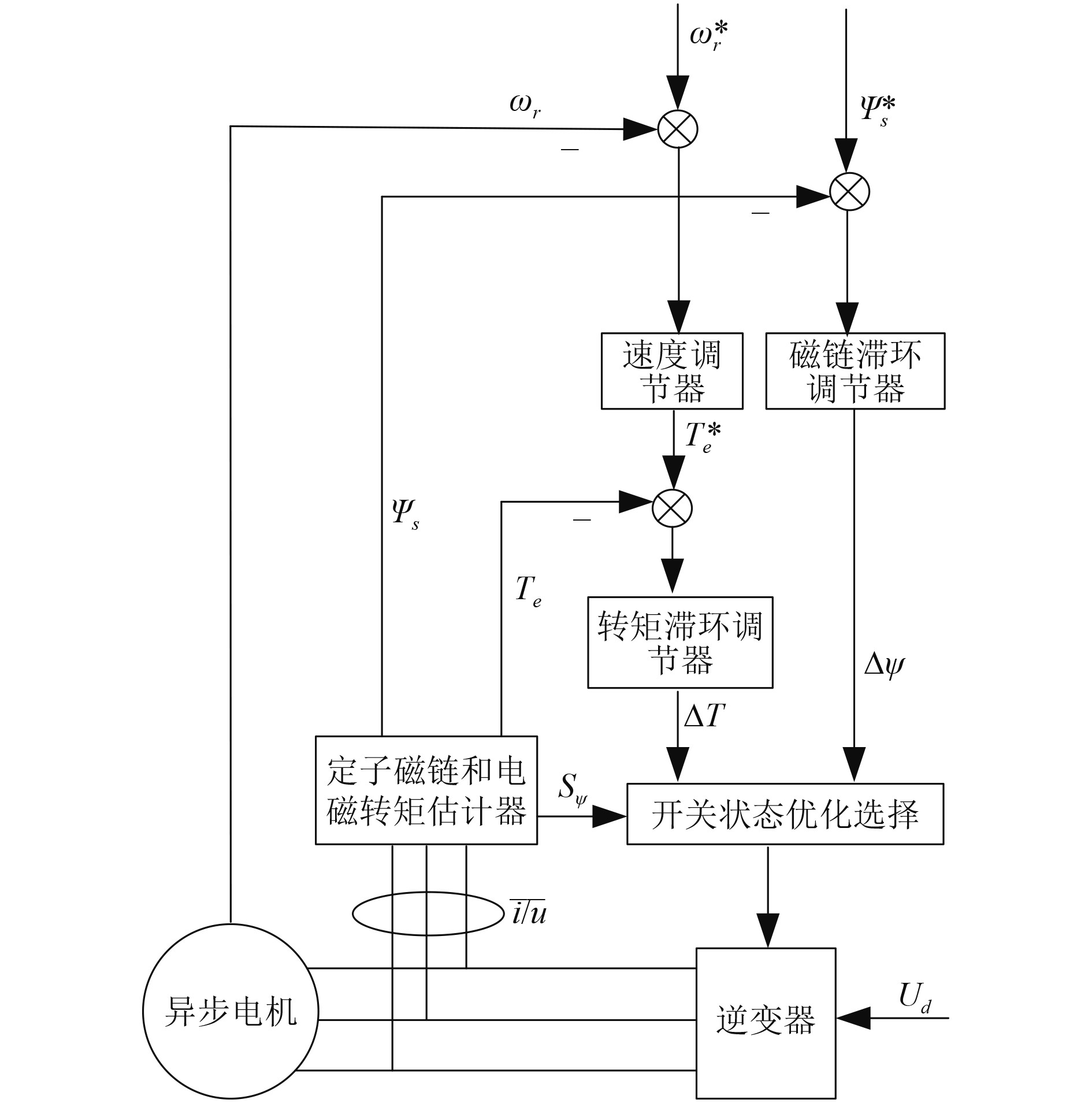
2.2 异步电机直接转矩控制技术船舶异步电机直接转矩控制系统的结构如图5所示。
|
图 5 异步电机直接转矩控制系统 Fig. 5 Direct torque control system of asynchronous motor |
可以看出,通过3/2坐标变换,获得异步电机定子相电压以及相电流在α~β坐标系下的值,然后通过定子磁链和电磁转矩估计器解算出转矩Te,Ψs以及磁链位置SΨ;速度调节器以实际测量得到的电机转速以及电机的期望转速为基础,解算出异步电机的给定转矩T* e,然后转矩滞环调节器以转矩Te以及T* e为基础,计算出转矩控制信号ΔT;通过测量的磁链Ψs以及期望磁链Ψ* s,磁链滞环调节器能够解算出控制信号ΔΨ,并通过ΔΨ来控制磁链;开关状态优化选择器根据位置SΨ、控制信号ΔT以及ΔΨ,并结合开关状态表的对应关系,得出最合适开关状态,并用该状态来控制逆变器,使得异步电机可以正常工作。
3 结 语船舶电力推进技术有着广泛的应用前景,随着船舶异步电机系统控制技术的快速发展,交流调速传动技术在电力电子、数字控制等技术的迅猛发展下也得到了快速发展。从长远角度来看,船舶电力推进系统会使用异步电机作为动力源。作为现代舰船动力的发展方向,船舶综合全电力推进系统得到了广泛的研究。
| [1] |
纪丹. 高压整流技术在舰船电力推进系统中的应用[J]. 舰船科学技术, 2021, 43(20): 97-99. |
| [2] |
张一驰. 基于矢量控制技术的舰船电力推进系统电机建模与仿真[J]. 舰船科学技术, 2019, 41(2): 109-111. |
| [3] |
宋艳琼, 陈辉, 高海波. 基于直接转矩控制技术的电力推进船Saber仿真[J]. 钦州学院学报, 2016, 31(4): 6-9. |
| [4] |
彭婧. 舰船电力推进系统工作性能的仿真分析[J]. 舰船科学技术, 2021, 43(24): 64-66. |
| [5] |
王孟莲, 沈枫. 舰船电力推进系统故障仿真软件关键技术研究[J]. 交通信息与安全, 2010, 28(6): 5-7. |
| [6] |
张玉婷, 卢青波. 舰船电力推进系统建模与稳定性研究[J]. 舰船科学技术, 2021, 43(12): 82-84. |
| [7] |
冯成. 舰船电力推进系统数字化开发环境浅析[J]. 船电技术, 2009, 29(7): 60-63. |
| [8] |
朱炜. 浅谈舰船综合电力推进系统及其相关技术[J]. 船电技术, 2014, 34(12): 14-18. |
| [9] |
韩旗. 区域配电网络在舰船电力推进系统中应用与发展[J]. 船电技术, 2011, 31(2): 33-36. |
| [10] |
宋文祥, 乐胜康, 吴晓新等. 一种改进的异步电机模型预测直接转矩控制方法[J]. 上海大学学报, 2018, 24(6): 861-876. |
| [11] |
王宇, 邓智泉, 王晓琳. 无轴承异步电机的直接转矩控制技术研究[J]. 中国电机工程学报, 2008(21): 80-84. |
| [12] |
党建军, 丁华伟. 直接转矩控制技术在三相异步电机控制中的应用研究[J]. 煤矿机械, 2012, 33(4): 198-199. |
 2022, Vol. 44
2022, Vol. 44
