0 引　言

现代大型舰船柴油机的机械装置和系统复杂庞大，运行工况多变，传感器监测参数众多。传统的实船试验、装置陆上试验及主机台架试验等研究手段过程繁杂，耗费大，调试周期长，在很多情况下难以实现。在这种情况下，采用仿真研究的方法对大功率舰用柴油机的运行特性进行预测和研究具有重要的理论意义和应用价值。

根据研究目的不同，研究者从不同研究角度出发，建立了多样化的柴油机模型。Hendrick E.^[1]建立了用于非线性控制与状态观测的平均值模型，但模型忽略了缸内燃烧过程的计算，细致程度不足。Latorre^[2]基于准稳态的概率，用一系列平衡点代替柴油机动态过程的变化值，建立了准稳态模型，但模型依赖大量的实验数据，通用性不强。Watson建立的容积法模型，可以研究燃烧放热、进排气规律^[3]，得到了大量应用：Rakopoulos，Hountalas等^[4-5]采用容积法建立柴油机多缸模型，用于柴油机广泛的参数研究和灵敏度分析，但其基于块图的因果式建模方法存在建模效率低、模型抽象不能反映柴油机实际工作原理等问题。李方玉^[6]利用GT-Power建立了柴油机容积法模型，并对柴油机性能故障进行了模拟分析，但存在的问题是模型具体实现方式并不可见，且建立的柴油机模型不能用于整体舰船柴油机动力装置联合仿真^[7]。

1996年，欧洲仿真协会综合多种建模语言的优点，设计出了全新多领域建模语言Modelica^[8]。Modelica语言建模具有以下特点^[9]：1）模型重用性和可扩展性强。Modelica采用分层机制与继承机制，实现模型模块化与层次化的设计。2）面向多学科领域统一建模。Modelica语言基于能量流守恒原理提出连接器的概念，让不同专业组成的大型系统可以在同一建模平台下进行构建。3）构建模型效率高。Modelica语言构建系统时直接按照系统拓扑关系，通过数学方程描述系统行为，无需对系统进行数值上的解耦和复杂系统算法求解序列的推导。

为满足正常和故障状态下对多种型号舰用柴油机主要监测参数进行性能仿真，进而预测其运行特性的需要，本文采用Modelica语言，研究建模效率、模型细致程度、模型通用性更高的柴油机建模方法，设计和建立大功率四冲程舰用柴油机通用模型库，在Mworks平台上进行模型集成和校核。在建立模型的基础上，对柴油机在故障状态下的性能进行预测和分析。

1 模块划分与模型库设计

Breunese^[10]提出自顶向下的模型库分为技术层、物理概率层、计算层3层结构。其中，技术层对应系统实际结构的划分，物理概率层对应相应技术层的描述方法而计算层则是将物理概率层的方法用方程的形式进行表达。

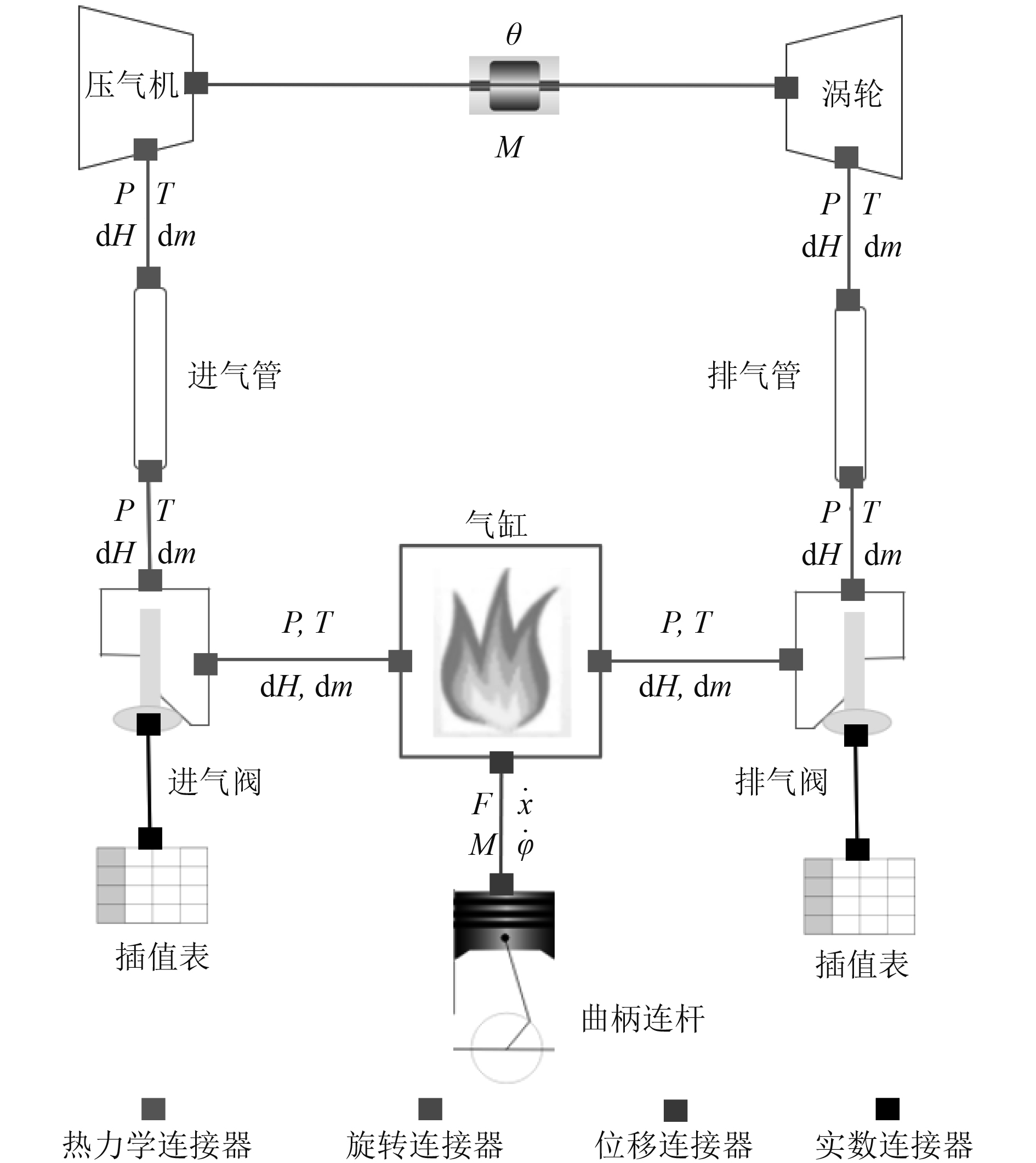
Modelica所具备的面向对象建模、多领域统一建模和非因果建模的技术优势很好的契合了构建此种3层模型库结构的要求。采用这种柴油机模型库结构的好处是，在对同一个柴油机系统模型进行不同设备的调换时，可通过对对应各层中的部件进行修改而不需要修改其他部件，增加了模型库的通用性。本文构建的柴油机系统模型库结构如图1所示，通过柴油机实际结构将其在图中涉及的相关概念将依次给出。

2 Modelica语言建模方法

传统建模语言进行建模，须将实际系统中各个对象之间的相互作用关系转换成数据内部对数据的操作^[10]。Modelica试图消除这种转换过程，使建模者能够以直观对象的概念建立仿真模型。这一思想的核心便是Modelica的连接机制与非因果建模能力。

2.1 连接器与连接机制

Modelica语言通过嵌入模型的连接器传递与物理系统相符合的势变量（也称横跨变量）和流变量（也称穿越变量），实现数据流的传递。其中流变量用关键词“flow”进行限定。一般而言，势变量代表了系统的驱动力，流变量代表在势变量下驱动的流量。柴油机系统不同模块的势变量和流变量如表1所示。

连接器所描述的各种物理量通过连接器的连接确立相互联系。

定义一个连接，如connect(Heatport1,Heatport2)，2个连接器形成一个连接节点并产生势变量相等且流变量和为0的2组方程：

$ T_{1}=T_{2} ，P_{1}=P_{2} ，$

(1)

$ d m_{1}+d m_{2}=0{\text{，}} d H_{1}+d H_{2}=0 。$

(2)

连接器与连接机制，反映了实际物理连接点的能量平衡、动量平衡或质量平衡，是广义基尔霍夫定律的体现，是实现多领域统一建模的基础。

2.2 非因果建模

常见的过程式数学描述（m语言、C语言等）建模，方程需经过人为处理为因果赋值形式才能用于描述模型行为，对方程的分析与转化将占据建模者大量的时间与精力。Modelica语言直接利用方程描述模型的行为，无需建模者编写模型求解序列，以气缸中理想气体状态方程为例:

$ PV = mRT ，$

(3)

当以质量 $ m $ 、体积 $ V $ 和气体常数 $ R $ 作为参数时，蕴含了2种可能的赋值形式：

$ T:=\frac{P V}{m R} ，$

(4)

$ P:=\frac{m R T}{V}。$

(5)

运算符号“ $ : = $ ”表示将等式右边的值赋给左边变量。方程可以根据数据环境的需要用于求解不同的变量，且方程的求解方向由Modelica仿真平台根据方程系统的数据流环境自动确定。

建立气缸模型时，将燃烧方程、放热率方程、容积变化方程等表征柴油机工作过程的方程内聚于一个组件模型之中，只要满足方程数与变量数相同，编译器将对方程进行编译，仿真平台将自动求解所有的变量值进行求解。这一特性使得建立柴油机模型时不必进行方程的转化推导，极大的减轻了建模工作量，有利于创建“高内聚，低耦合”的柴油机模型。

3 柴油机模型库建立

针对柴油机系统模型库技术层划分的不同模块以及模块间的能量及物质交换关系，建立了热力连接器、位移连接器、旋转连接器和实数连接器，实现方法见图1。在建立好连接器的基础上，对各个模块构建其组件模型，从其物理概念层出发，运用对应技术层的数学公式或计算方法依次建立了涡轮增压器、气缸、进排气阀、中冷器、曲柄连杆机构等模型。

3.1 气缸模型 3.1.1 燃烧模型

燃料燃烧放热规律的计算公式为：

$ \frac{{{\rm{d}}{Q_f}}}{{{\rm{d}}\phi }} = {m_f}{H_u}\frac{{{{\rm{d}}_x}}}{{{{\rm{d}}_\phi }}} 。$

(6)

式中： $ {m_f} $ 为单缸循环喷油量； $ {H_u} $ 为燃油燃烧低热值； $ x $ 为燃料燃烧百分数。

采用双韦伯燃烧放热方程，将燃烧过程分为预混合燃烧和扩散混合燃烧两部分计算燃料燃烧速率从而得到燃烧放热率，即

$ \frac{{{\rm{d}}x}}{{{\rm{d}}\phi }} = \frac{{{{\rm{d}}_{x1}}}}{{{{\rm{d}}_\phi }}} + \frac{{{{\rm{d}}_{x2}}}}{{{{\rm{d}}_\phi }}} 。$

(7)

式中： $ {x_1} $ 和 $ {x_2} $ 分别为预混合及扩散燃烧的燃料分数。

3.1.2 气缸散热模型

根据工质对气缸周壁的瞬时换热系数 $ a_{g} $ 和壁面平均温度 $ T_{\mathrm{we}} $ ，可以对气缸散热率进行计算：

$ \frac{{\rm{d}}{Q}_{w}}{{\rm{d}}\phi }={\displaystyle \sum _{1}^{3}{a}_{g}} \cdot {A}_{i}(T-{T}_{wi})。$

(8)

式中： $ a_{g} $ 为瞬时换热系数； $ A $ 为换热面积； $ T_{\mathrm{we}} $ 为壁面平均温度；

瞬时换热系数 $ a_{g} $ 的计算采用Woschni G.根据内燃机实验数据整理得到的公式，即

$ {a}_{g}=110 \cdot {d}^{-0.2}{P}^{0.8}{T}^{-0.53}\left[{c}_{1}{c}_{m} + {c_2}\frac{{{V_S}{T_1}}}{{{P_1}{V_1}}}(P - {P_0})\right]^{0.8}。$

(9)

式中： $ {c_m} $ 为活塞平均速度； $ {c_1} $ 为气流速度系数； $ {c_2} $ 为燃烧室形状系数； $ {V_S} $ 为气缸工作容积； $ {P_0} $ 为发动机倒拖时缸内压力；

单缸模型建立完成后，采用“缸平移”法，按照发火间隔进行叠加建立柴油机多缸模型，以16缸柴油机为例，其发火间隔角为45°，通过柴油机转速可以计算得到发火间隔时间，将该时间依次输入16个变量推移模块，即可得到16缸柴油机模型。以此类推可依据模型库建立不同缸数的四冲程柴油机模型。

3.2 进、排气系统模型

将进、排气过程假定为空气流经面积变化的孔板的一维等熵绝热流动。

排气分为2个阶段，初期排气阶段由于缸内与排气管内压差较大，可能出现超临界流动；之后，随着压差的减小，转为亚临界流动。

当 $\dfrac{{{P_e}}}{P} \leqslant {\left(\dfrac{2}{{k + 1}}\right)^{\tfrac{k}{{k - 1}}}}$ ，为超临界流动，排气流量变化率为：

$ \frac{{{\rm{d}}{m_e}}}{{{\rm{d}}\varphi }} = \frac{1}{{6n}}{\mu _e}{A_e}\frac{P}{{\sqrt {RT} }}{\left(\frac{2}{{k + 1}}\right)^{\frac{1}{{k - 1}}}}\sqrt {\frac{{2k}}{{k + 1}}} ，$

(10)

当 $ \dfrac{{{P_e}}}{P} > {\left(\dfrac{2}{{k + 1}}\right)^{\tfrac{k}{{k - 1}}}} $ ，为亚临界流动，排气流量变化率为：

$ \frac{{{\rm{d}}{m_e}}}{{{\rm{d}}\varphi }} = \frac{1}{{6n}}{\mu _e}{A_e}\frac{P}{{\sqrt {RT} }} ，$

$ \sqrt {\frac{{2k}}{{k - 1}}\left[ {{{\left(\frac{{{P_e}}}{P}\right)}^{\frac{2}{k}}} - {{\left(\frac{{{P_e}}}{P}\right)}^{\frac{{k + 1}}{k}}}} \right]} 。$

(11)

式中： $ u_{e} $ 为排气流量系数； $ A $ 为排气阀几何流动截面积； $ P_{e} $ 为排气管内压力； $ \boldsymbol{k} $ 为缸内绝热指数。

进气阀处气体的流动均属于亚临界流动，其流量计算同式（11）。

3.3 增压系统模型

舰船大功率柴油机增压形式大致有3种：等压增压、脉冲增压、MPC增压。在模型库中，首先建立等压增压系统模型。

将增压器划分为涡轮、压气机和转子3部分，分别建立模型。其中，利用压气机稳态特性图对压气机压比与增压器转速进行二维线性插值，得到流量与效率，进一步得到增压器出口温度和扭矩为：

$ {T_{ce}} = {T_{cs}}[1 + (1 - {\pi _k}^{ - \frac{{k - 1}}{k}})/{\eta _c}] ，$

(12)

$ {M}_{c}={c}_{p}\stackrel{·}{{m}_{c}}(1-{\pi }_{k}{}^{-\frac{k-1}{k}})/({\eta }_{c}{n}_{tc}) ，$

(13)

式中： ${T_{ce}}$ 为压气机出口温度； ${T_{cs}}$ 为压气机进口温度； ${\pi _k}$ 为压气机增压比； $k$ 为空气绝热指数； ${\eta _c}$ 为压气机效率； ${M_c}$ 为压气机扭矩； $ \stackrel{·}{{m}_{c}} $ 为压气机流量。

同理，利用涡轮稳态特性图，根据压比，查表得到涡轮流量系数与效率，再将涡轮等效为一个喷嘴模型，可求得通过该喷嘴的质量流量为：

$ \stackrel{·}{{m}_{T}}={u}_{t}\cdot {F}_{res}\cdot \sqrt{2\cdot {P}_{T}\cdot {\rho }_{T}}\cdot \phi ，$

(14)

式中： $ \stackrel{·}{{m}_{T}} $ 为排气质量流量； ${u_t}$ 为流量系数； ${F_{res}}$ 为喷嘴等效面积； $\phi $ 为流量函数。

进而求得涡轮输出的扭矩为：

$ {M}_{t}={c}_{p}{}_{e}\stackrel{·}{{m}_{t}}{\eta }_{t}{T}_{e}(1-{\pi }_{k}{}^{-\frac{k-1}{k}})/{n}_{tc} 。$

(15)

式中： $ {M_t} $ 为涡轮扭矩； $ {c_p}_e $ 为排气定压比热； $ {\eta _t} $ 为涡轮效率； $ {n_{tc}} $ 为涡轮增压器转速。

转子模型由牛顿定律得到，可求得增压器转速为：

$ {n_{tc}} = \frac{{{\eta _m}{M_T} - {M_c}}}{{{J_{tc}}}} \cdot \frac{{30}}{\pi } 。$

(16)

式中： $ {\eta _m} $ 为涡轮增压器机械效率； $ {J_{tc}} $ 为转子转动惯量。

在等压增压模型建立的基础上，可以通过改变柴油机排气系统模型实现其他增压形式的转换。以相继增压系统为例，可通过在两列排气管间增加连通管、基本增压器压气机前增加空气阀、涡轮后增加燃气阀的方式建立相继增压模型。

4 模型验证与稳态仿真分析

以某型舰用16PC2-6柴油机为研究对象，该柴油机为PIELSTICK系列的中速柴油机，被广泛用于船舶推进主机。其主要性能参数如表2所示。

在仿真平台Mworks上，依据所建立的模型库，搭建了该型柴油机系统整体模型，并标出了对应势变量于流变量，如图2所示。可以看出，基于Modelica语言的建模因为其非因果的特性，使模型遵循了物理系统的实际拓扑结构，同时由于模型库子模型采用了规范统一的连接器，因此在该模型的基础上，可以通过添加子模型、修改结构参数等方法，较为方便的将其转换为结构参数不同的其他柴油机模型。

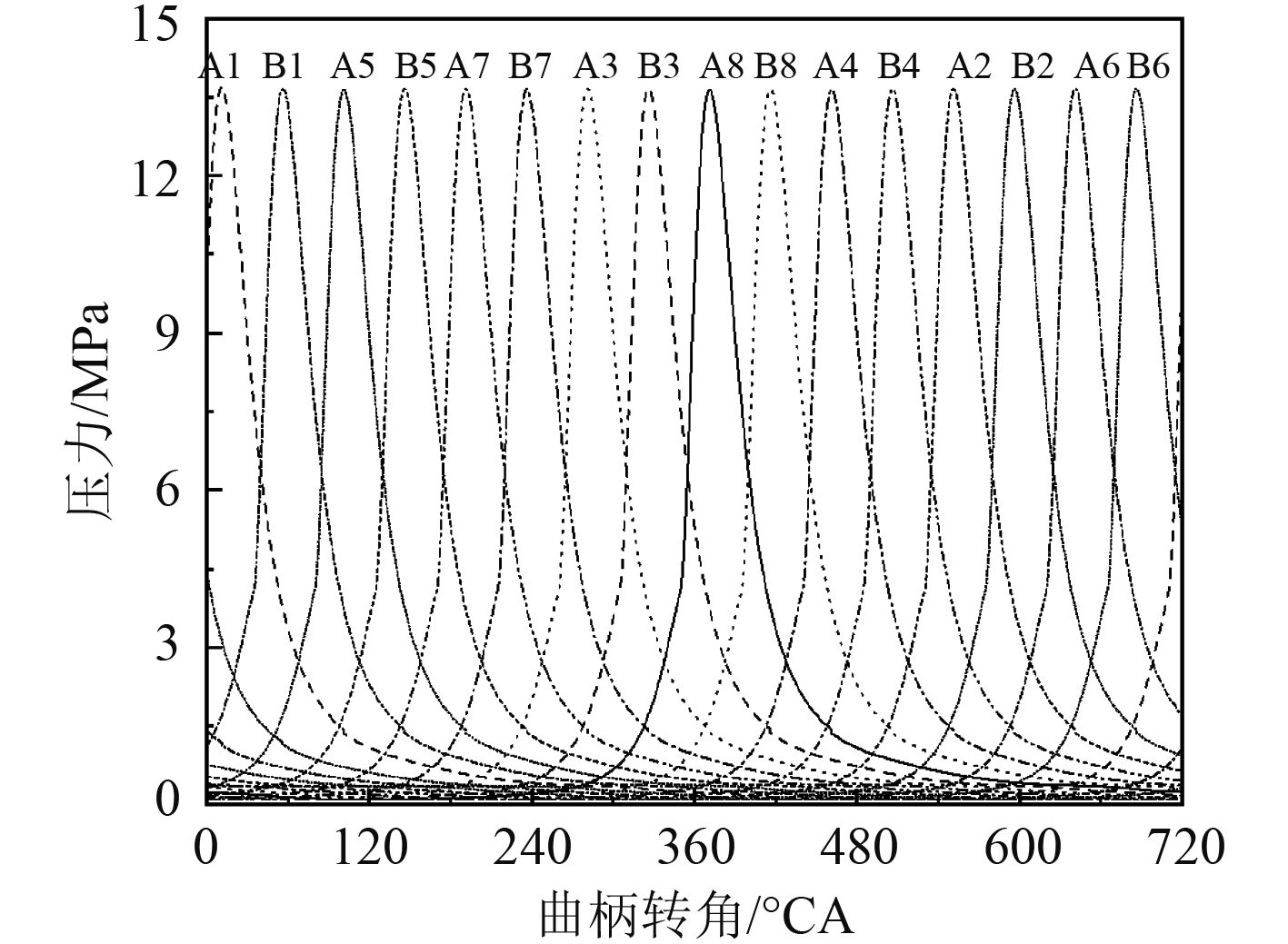
选定额定工况的各项边界条件对该柴油机模型进行仿真，得到整机多缸压力随曲柄转角变化情况如图3所示。V型排列的A和B两列气缸均按照1-5-7-3-8-4-2-6的发火顺序依次发火燃烧，缸内最高压力为13.7MPa，发火间隔角为45º。

为验证模型的准确性和可靠性，分别对该型柴油机不同工况进行仿真分析并与实验数据进行对比。仿真得到的结果数据与实验数据的对比情况如表3所示。各项特性参数误差范围均在5%以内，说明该模型具备较高的准确性。

5 典型故障仿真分析

以喷油定时故障和单缸喷油不均为例，通过在原有模型上设置故障系数、改变模型参数的方法来设定故障进行故障仿真。同时，选取表征柴油机工作状态与性能指标的参数：有效功率 $ {P_e} $ 、燃油消耗率 $ {g_e} $ 、输出转矩 $ M $ 、缸内爆发压力 $ {P_m} $ 、燃烧最高温度 $ {T_m} $ 、气缸排气温度 $ {T_e} $ 。通过计算故障工况下参数相对正常工况下参数的偏移率来分析故障对系统的影响。

5.1 喷油定时故障

喷油定时故障分为喷油过早与喷油过晚。该柴油机正常工况喷油提前角为15°，按故障严重程度的不同选取喷油提前角5°和10°为喷油过晚故障，选取喷油提前角20°和25°为喷油过早故障。

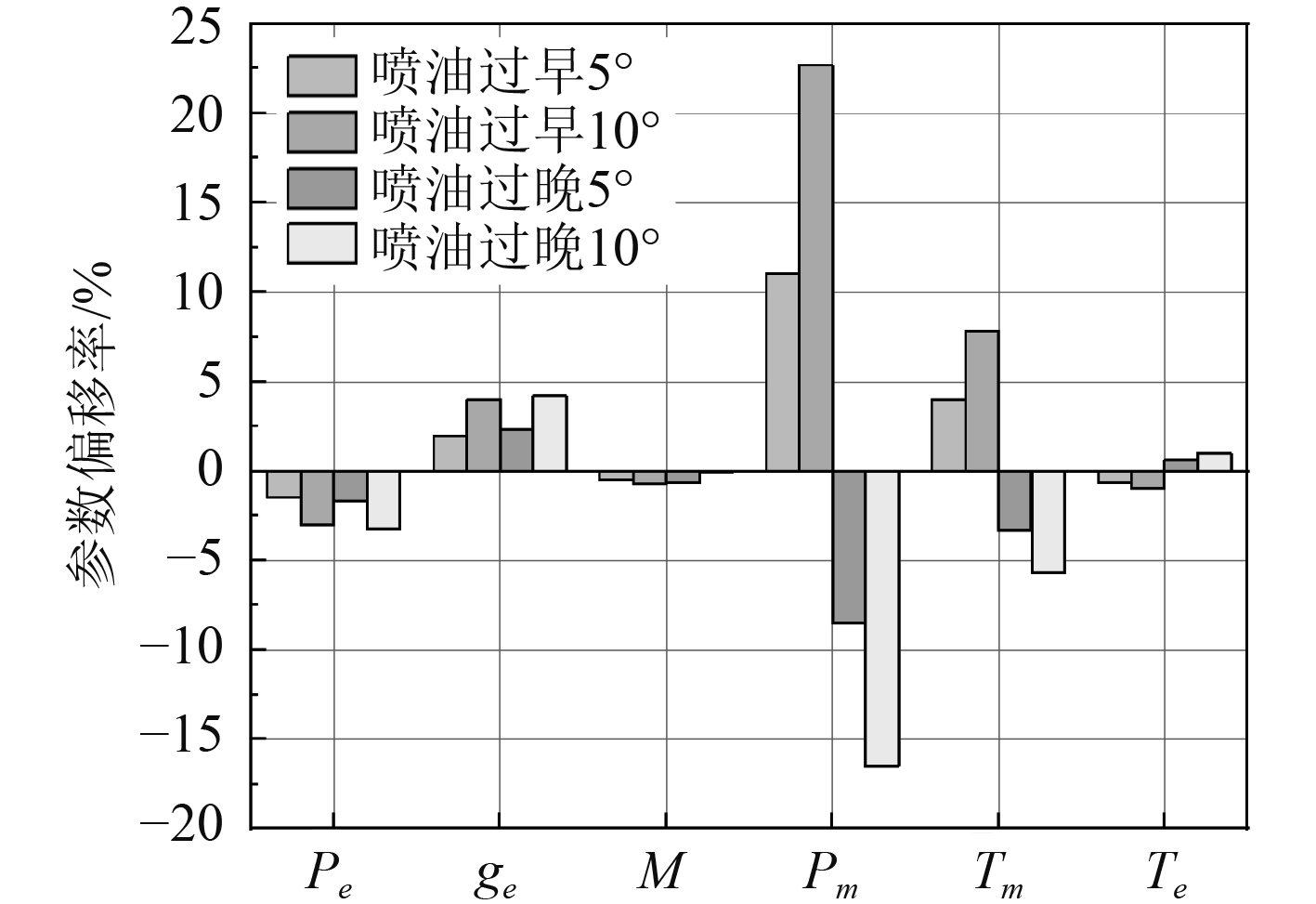
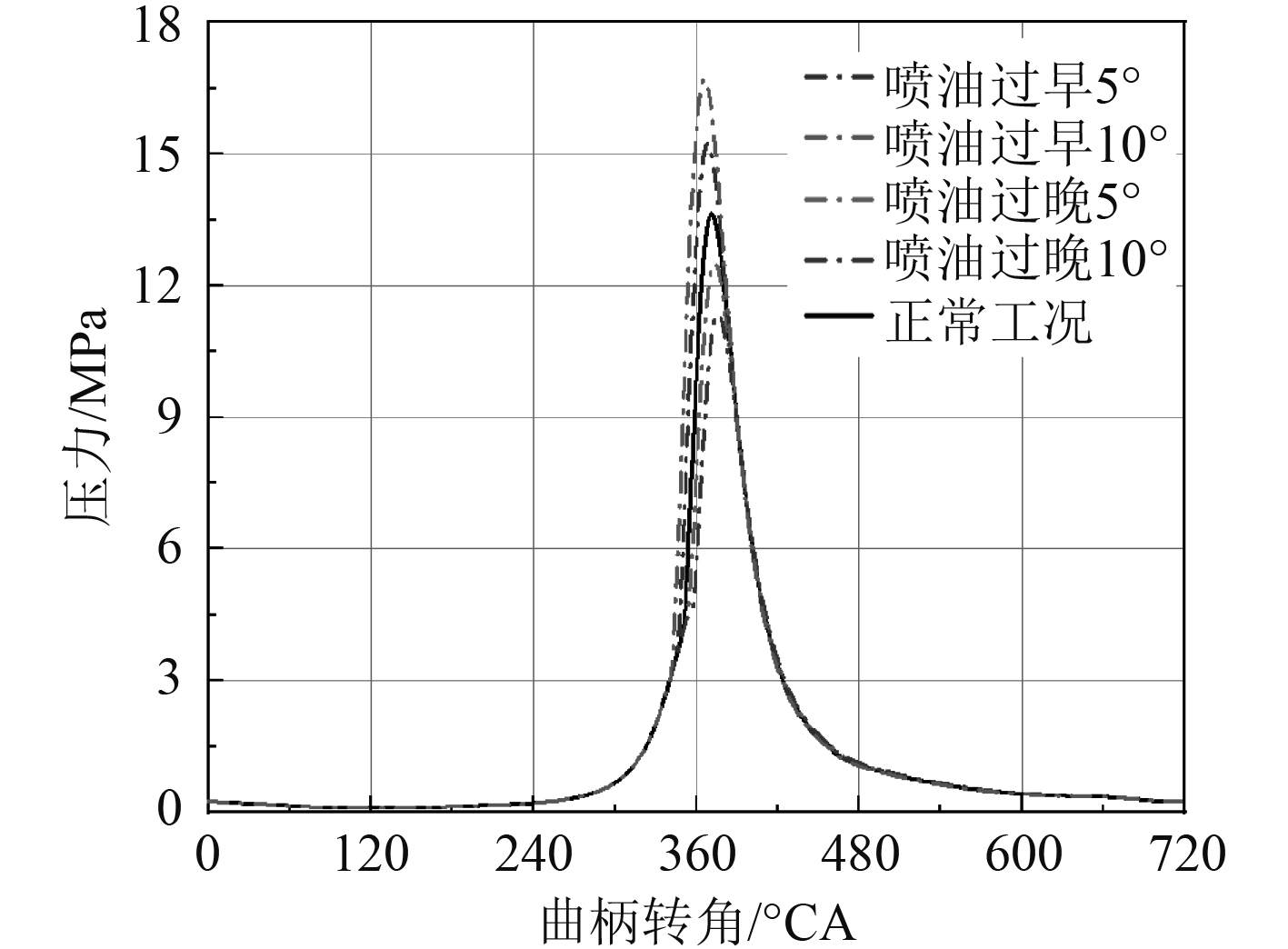
如图4和图5所示，喷油过晚时，柴油机功率、输出转矩略有降低，燃油消耗率上升。同时缸内最大爆发压力、燃烧最高温度降低，排气温度升高。其主要原因是：发生故障时，喷油提前角减小，供油时间滞后，使得气缸压缩阶段喷入燃油质量减小，膨胀阶段喷油燃油质量增加，导致了燃烧阶段的后移，最大爆发压力出现时间后移。

喷油过早时，柴油机功率、输出转矩、燃油消耗率上升，缸内最大爆发压力、燃烧最高温度升高，排气温度降低，出现最高爆发压力的活塞位置越接近上止点。其主要原因是：发生故障时，喷油提前角增大，供油时间提前，使得燃烧过程急燃期前移，导致产生最大爆发压力时间提前。同时燃烧的后燃时间缩短，排气温度降低。

喷油定时故障下，偏移程度最大的参数为 $ {P_m} $ ，在最大故障程度下，其偏移率达到了23.2%，其次是 $ {T_m} $ ，其最大偏移率达到了8.7%，其余各参数偏移率均在5%以内。喷油定时关系到柴油机整个燃烧过程，可通过柴油机特性参数的上述变化规律作为判断柴油机是否处于喷油定时故障的重要依据。

5.2 单缸喷油器堵塞

正常工况下，该型柴油机单缸循环喷油量 $ {m_f} $ 为6.3 g/cycl。发生单缸喷油器堵塞时，按照故障严重程度的不同，引入故障程度系数K，则故障条件下单缸循环喷油量 $ {m_{ff}} = K \cdot {m_f} $ 。针对不同的故障严重程度，分别取K=0.8，K=0.5，K=0.2对应故障程度逐渐恶化的3种工况。

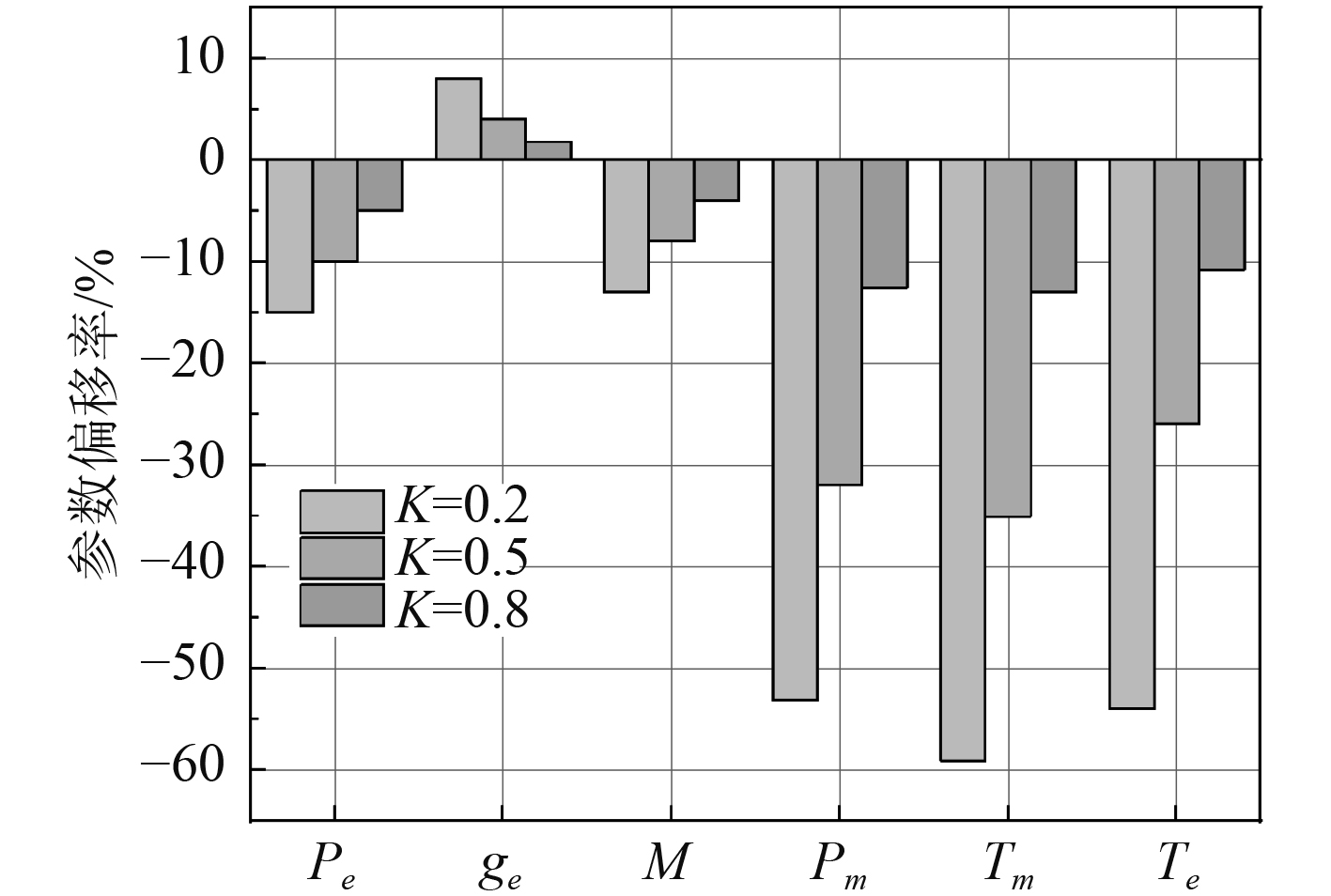
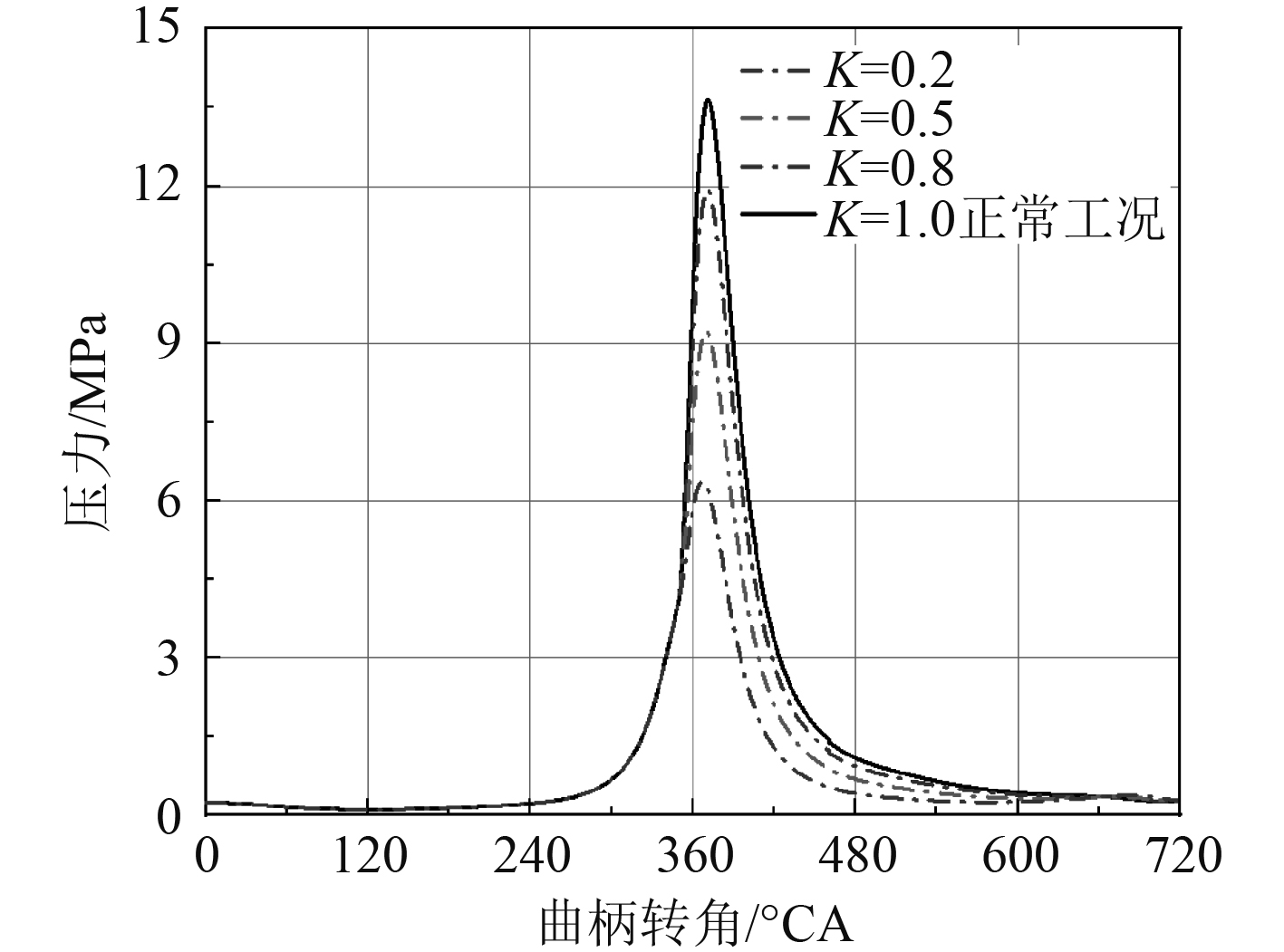
发生单缸喷油器堵塞故障，导致柴油机气缸单缸循环喷油量降低，如图6和图7所示。柴油机功率、输出转矩降低，燃油消耗率上升，这是因为单缸喷油量的减少导致柴油机输出功率的下降，调速器会增大其余各缸的循环喷油量，导致燃油效率上升。同时，缸内爆发压力、燃烧最高温度、排气温度随着喷油量的减少而明显降低。

单缸喷油器堵塞故障下，参数 $ {T_m} $ ， $ {P_m} $ ， $ {T_e} $ 均出现较大的偏差，在最大故障程度下，其偏移率分别达到了−51.4%，−58.9%，52.7%，其余各参数偏移率均在10%以内。可通过柴油机特性参数的上述变化规律判断柴油机是否处于喷油定时故障。

6 结　语

本文以某舰用四冲程柴油机为研究对象，从柴油机实际工作过程及其基本物理规律出发，对柴油机系统进行模块化分解，在仿真平台Mworks上，运用Modelica语言建立了符合柴油机实际拓扑结构且具有较好通用性的柴油机模型库，在基于模型库的基础上，搭建了舰用16PC2-6柴油机模型，模拟了柴油机喷油定时故障、喷油器堵塞对柴油机系统的影响。结果表明：

1）Modelica语言非因果建模与面向对象建模的特性使得建模者能够更高效的完成模型的建立，使得系统间物质与能量转换关系更加清晰明了，增加了模型的通用性与可读性。

2）通过仿真实验和故障模拟，证明了所建立的柴油机模型具有较高的精度与可靠性，可用于分析故障工况下参数的改变对柴油机性能的影响，得到了不同故障状态下柴油机监测参数的变化规律，为进一步的故障诊断工作建立研究基础。