2. 大连理工大学 海洋科学与技术学院,辽宁 盘锦 124221
2. School of Ocean Science and Technology, Dalian University of Technology, Panjin 124221, China
随着新能源技术的不断发展以及我国政策上对新能源的重视,海上风电得到迅速发展,渤海与黄海海域因其所处海域纬度较高,受冷空气影响,较中国其他海域空气密度更高,风能密度大,所以是我国发展海上风电的重点海域[1-3]。但在冬季由于寒潮和冷空气的不断侵袭,冰情却很严重,这会导致一系列严重的工程问题,使结构物发生破裂、倾斜,甚至造成结构物坍塌的灾难性事故[4-5]。海上风机塔筒及基础同时耦合了高耸结构、大型动力设备基础和海洋工程3种结构特征,风机振动对风机结构及发电设备影响比较大,因此,海上风电基础结构也成为海洋工程结构抗冰设计需要考虑的典型结构物[6-7]。
冰与结构的相互作用是一个相互耦合的过程。冰与结构的相互作用与结构的形式有很大关系,结构形式不同对冰力的形式、大小以及冰力机理都有很大的影响。现有海洋工程结构根据迎冰面的不同,可以分为直立结构和锥体结构[8]。冰荷载包含静冰荷载与动冰荷载,严重的静冰荷载会将结构推倒。动冰荷载会造成结构振动,振动是影响冰区海洋工程结构安全的重要因素。根据多年来对渤海海域石油平台的现场监测发现,海洋平台振动不仅影响设备的正常运行,并且长时间的疲劳积累,会造成结构过早疲劳失效[9]。
根据渤海海域某在建风电场的具体风机模型资料及海况条件,基于Ansys有限元分析,分别对海上风电基础加装锥体结构前后的抗冰性能做对比分析,包括极值静冰荷载下结构变形及强度分析、动冰荷载下结构的振动响应及疲劳分析,从而对海上风电基础结构加装锥体的抗冰设计效果做出评估。
1 海冰荷载 1.1 直立结构冰荷载 1.1.1 直立结构的极值冰力模型直立结构的静冰力按API-RP-2N在结冰环境中的海上固定结构的计划、设计和建造规范给出的公式进行计算[10],如下式:
| $ F=KDh{\delta }_{c}。$ | (1) |
式中:F为总冰力,kN;K为折减系数,本文取K=1;D和h分别为结构直径和冰厚,m。
根据渤海导管架石油平台的原型监测数据,Kärnä得到自激振动冰力时程,并根据时程曲线给出简化的三角波时域函数[11],表征产生自激振动的冰力随时间的变化特征,如图1所示。
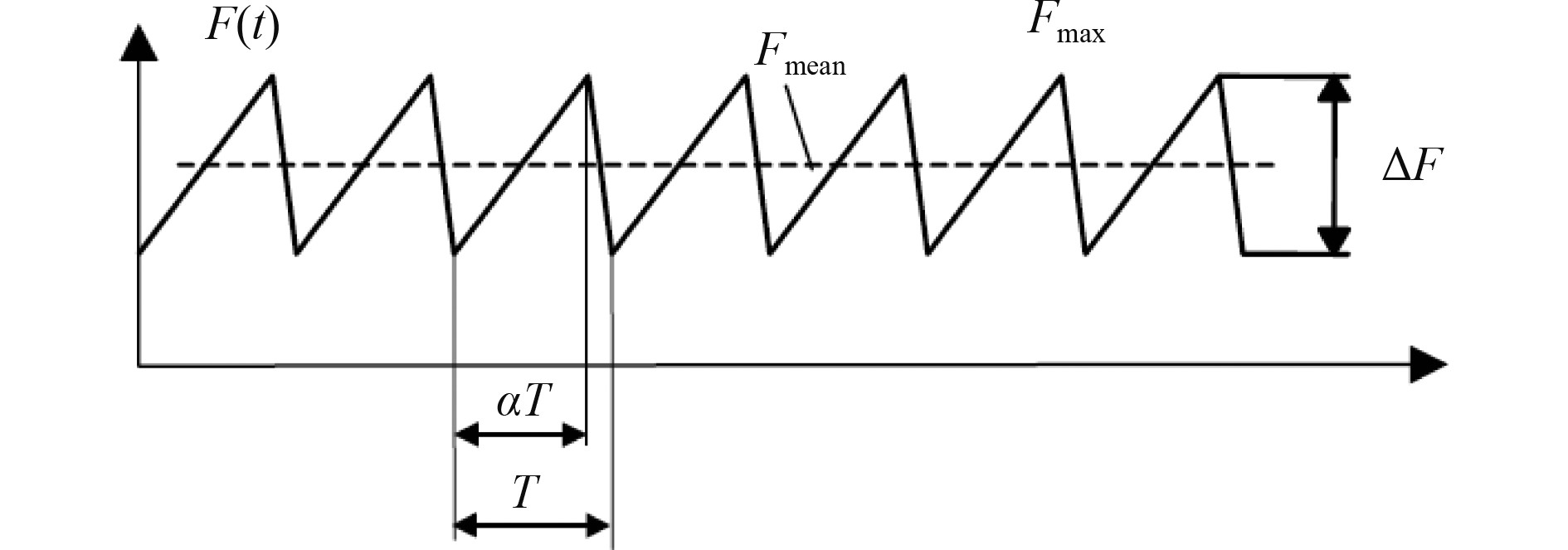
|
图 1 简化的稳态冰力模型 Fig. 1 Simplified steady-stable ice force model |
图中:Fmax为冰力最大值,可保守取为极值静冰力;
Hirayama-Obara[12]给出锥体结构上的极值静冰力公式:
| $ F = B{\sigma _f}{t^2}{\left(\dfrac{D}{{{L_c}}}\right)^{0.34}},$ | (2) |
| $ {L_c} = {\left(\dfrac{{E{t^3}}}{{12\rho g}}\right)^{0.25}} ,$ | (3) |
式中:
利用大量的现场观察,岳前进等[13]研究了冰与锥体结构相互作用过程,根据冰与锥体作用过程的受力分析,给出了冰块在锥体上破坏过程中的冰力变化情况。作用过程分为接触破坏阶段、爬升阶段、清除阶段。这一变化过程的冰力函数可以简化为如图2所示。
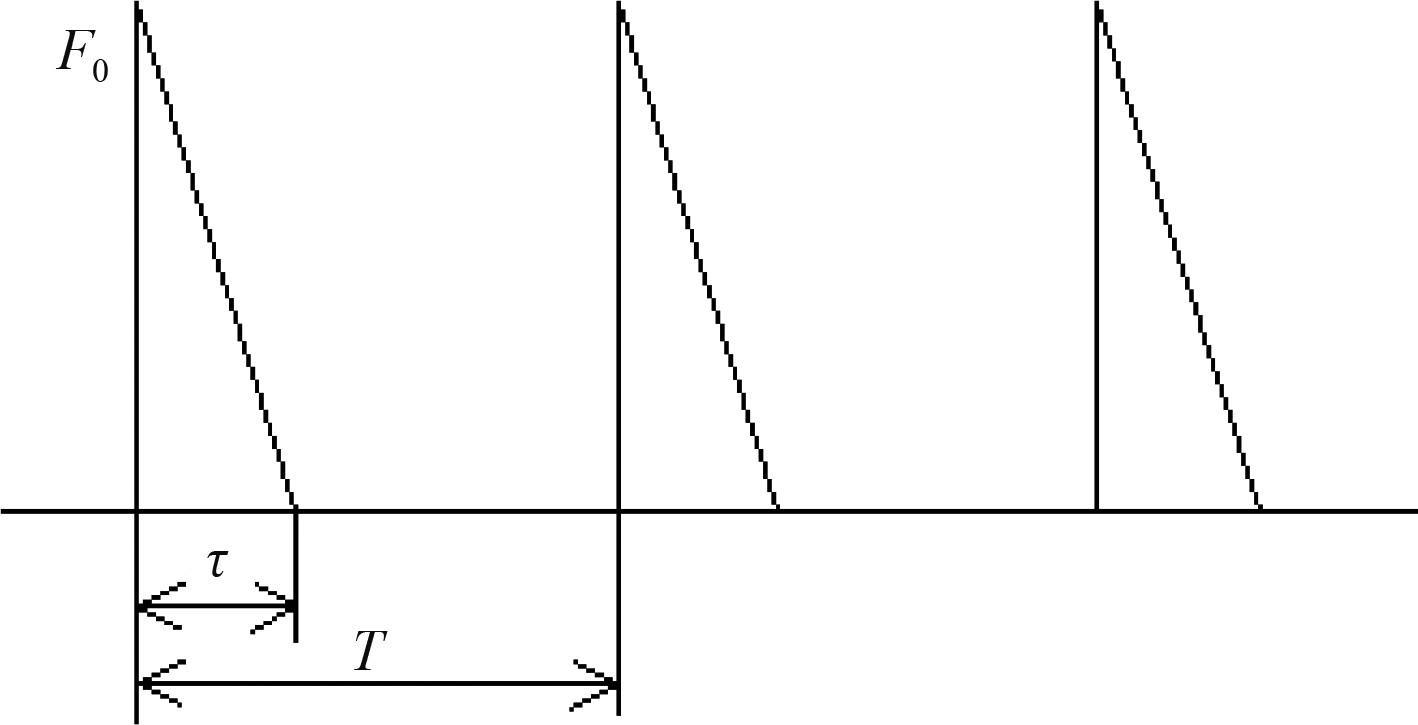
|
图 2 简化的冰力函数 Fig. 2 Simplified ice force function |
| $ F(t) = \left\{ {\begin{array}{*{20}{l}} {F_0}\left( {1 - \dfrac{t}{\tau }} \right) &{(0 \leqslant t < \tau )},\\ 0 &{(\tau \leqslant t < T)} 。\end{array}} \right. $ | (4) |
式中:F0为冰力幅值;T为冰力周期;τ为冰与锥体的作用时间。
F0建议取锥体结构的极值冰力,T为冰力的周期也是冰发生弯曲破碎的周期,可以由破碎长度与冰速决定:
| $ T = \dfrac{{{L_b}}}{V} = \dfrac{{kh}}{v}。$ | (5) |
由以上分析,风电锥体结构分析得到k取值为9.2;h为冰厚,m;v为冰速,m/s;通过渤海实测数据分析τ取1/3的冰力周期T。
1.3 直立结构冰力荷载谱Kärnä和Qu根据渤海和波斯尼亚湾灯塔上测得的大量样本的随机冰荷载数据,经过统计分析建立了随机冰力谱[14]:
| $ S_{F, F}(f)=\dfrac{\sigma_{F_{j}}^{2}}{f} \widetilde{S}_{F_j F_j}(f)。$ | (6) |
其中:自功率谱
为了进行频域的响应分析,需要建立冰荷载谱,段忠东等[15]曾利用现场数据对冰力谱形式进行了研究。利用多年积累的现场实测锥体冰力时程数据,建立了锥体的冰力谱[16],如下式:
| $ S(f)=\dfrac{10.88 \bar{F}_{0}^{2} \bar{T}^{-2.5}}{f^{3.5}} \exp \left(-5.47 \bar{T}^{-0.64} \dfrac{1}{f^{0.64}}\right)。$ | (7) |
式中:F0为锥体冰力幅值,
根据风机基础的结构参数,风机结构泥面以上高度101 m,平均海平面以上高度93 m,基于Ansys建立了结构模型。其中,风机采用SHELL单元;上部重量采用MASS21单元;采用6倍桩径法处理单桩基础,即泥面以下基础长度为基础直径的6倍,底部固定约束,此方法是建立固定式海洋工程结构有限元模型的常用方法[17]。平整冰作用位置为平均水平面位置,根据风机基础的结构参数及水文资料,设计锥体高5.2 m,锥角60°。
2.2 极值静冰力根据《中国海海冰条件及应用规定》,采用渤海北部海域冰况,对比分析直立结构和加装锥体2种不同形式的风机基础在50年一遇的冰况下(冰厚30 cm)结构的最大极值静冰力的变形和应力。
如表1所示,50年一遇的极端冰况下,加装锥体后风机基础结构的变形及应力强度大幅减弱。
|
|
表 1 极值冰力作用下结构的响应 Tab.1 Vibration response of offshore wind turbine foundation under extreme ice load |
基于建立的直立结构稳态冰力模型进行确定冰力函数,计算风机的动冰力时程,底部固定约束,利用Ansys瞬态分析方法,分析结构在动冰力下的响应情况,如图3~图5所示

|
图 3 静冰荷载作用下风机基础结构响应 Fig. 3 Vibration response of offshore wind turbine foundation under static ice load |
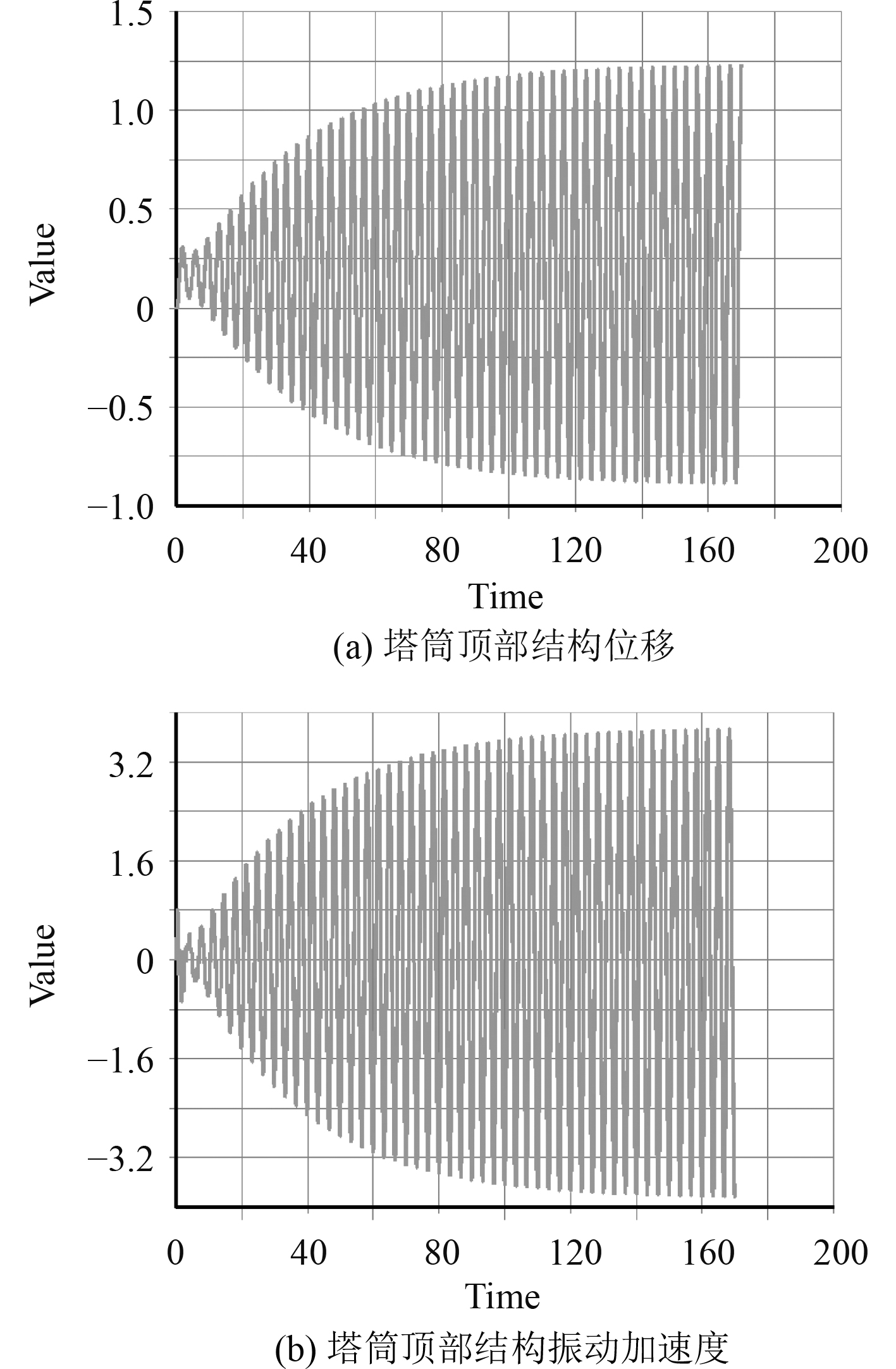
|
图 4 50年一遇直立风机结构冰振响应 Fig. 4 Vibration response of offshore wind turbine foundation in 50 years |
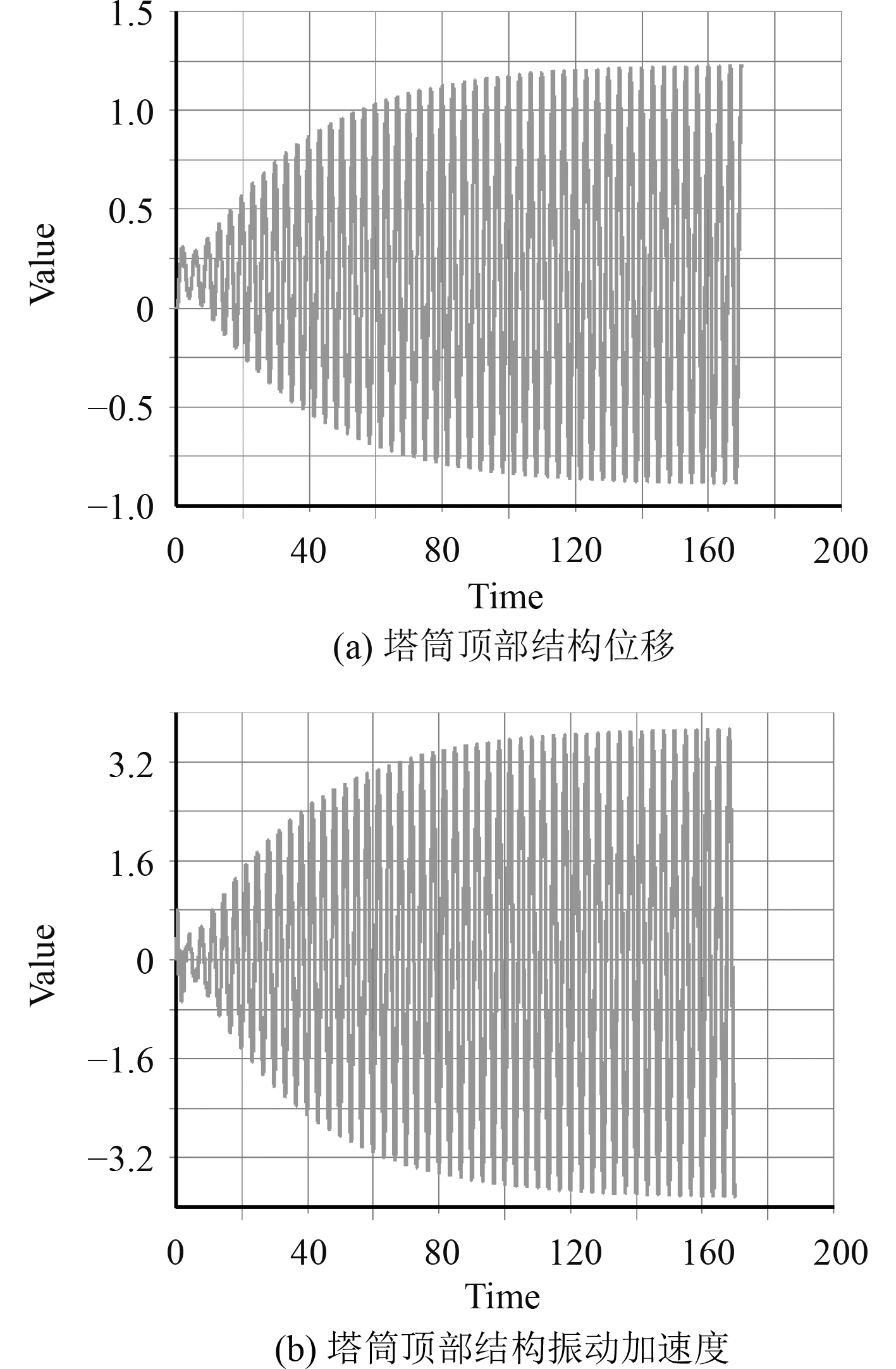
|
图 5 50年一遇加装锥体结构冰振响应 Fig. 5 Vibration response of the cone offshore wind turbine foundation in 50 years |
如表2所示,在50年一遇的极端冰况下,加装锥体后风机基础结构的振动响应大幅减弱。
|
|
表 2 塔筒顶部结构振动响应 Tab.2 Vibration response of the top offshore wind turbine foundation under extreme ice load |
通过整理分析渤海石油平台多年来的海冰监测数据,季顺迎得出海冰冰厚的概率密度函数为[18]:
| $ f(h) = \dfrac{1}{0.550\;3h\sqrt{2\text{π} }}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\dfrac{1}{2}{\left(\dfrac{\mathrm{ln}h-1.976\;4}{0.550\;3}\right)}^{2}\right] ,$ | (8) |
式中,h代表海冰厚度。
得到冰速的概率函数为:
| $ f( {V}_{i}) = \dfrac{{V}_{i}}{826.551\;2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\dfrac{{V}_{i}^{2}}{1\;653.102\;4}\right),$ | (9) |
式中:v代表海冰速度。
根据水文参数,采用冰厚0.04~0.3 m,以0.05 m为间隔,冰速0.05~0.8 m/s,0.1 m/s为间隔54种工况来进行计算。根据式(8)与式(9)计算得到冰速与冰厚的联合概率分布,54种冰况的发生概率如表3 所示。
|
|
表 3 冰况的发生概率 Tab.3 The probability of ice condition |
通过随机冰力谱数据,可以清晰地得到随机冰力的荷载谱。需要对每一组数据进行谱分析,总共54个工况下的分析数据。然后通过Ansys进行谱分析就可以得到疲劳分析结果。
通过提取各工况的热点处应力方差值来分析结构疲劳损伤。在随机冰振下直立结构的热点都主要在风机上部。
在随机冰振下,对塔筒热点进行疲劳寿命的分析,查询《中国海海冰条件应用规定》提供的海域平均有效冰期32天,计算的结构疲劳寿命见表4。
|
|
表 4 直立风电基础结构疲劳损伤(年) Tab.4 The fatigue injury of the upright offshore wind turbine foundation |
在随机冰振下,对风机上部热点应力进行疲劳分析得到一年结构总损伤0.00982,寿命约为101年。
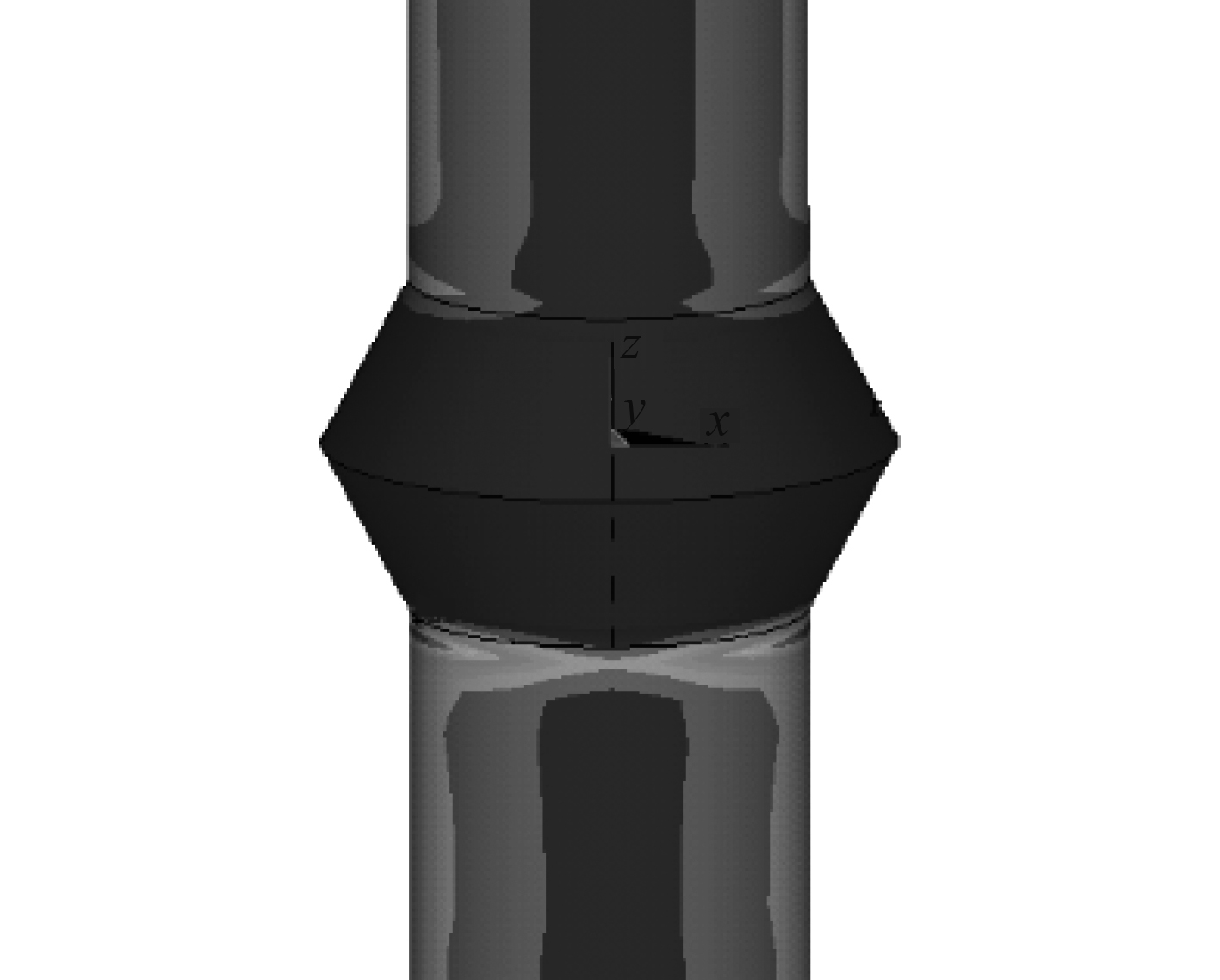
2.4.3 加装锥体风机基础结构的疲劳分析通过提取各工况的热点处应力标准差值来分析结构疲劳损伤。在随机冰振下风电基础的热点主要集中再加装锥体的下部,如图6所示。
|
图 6 加装锥体结构疲劳热点 Fig. 6 The hot spot location of the cone offshore wind turbine foundation |
在随机冰振下,对塔筒热点进行了疲劳寿命的分析,同样采用平均有效冰期32天,计算的结构疲劳寿命如表5所示。
|
|
表 5 加装锥体的风电基础结构疲劳损伤(年) Tab.5 The fatigue injury of the cone offshore wind turbine foundation |
在随机冰振下,对风机上部热点应力进行疲劳分析得到一年结构总损伤1.1×10–6。寿命约为909090年。
如表6所示,加装锥体极大的降低了结构的冰激疲劳损伤。
|
|
表 6 风机基础疲劳损伤对比 Tab.6 The comparison of fatigue |
利用有限元分析方法,分别对海上风电基础加装锥体结构前后的抗冰性能做了对比分析,结果表明风机基础在加装锥体结构之后抗冰性能大大提高,使得风电基础结构在近海冰区的环境适应性增强,加装锥体结构形式的应用将促进风电在近海有冰海域的充分发展,也为有冰海域内其他类型海洋工程结构的抗冰设计提供了可借鉴的思路。但是,仍有以下2个方面有待进一步分析:
1)加锥后水线处宽度增加,无冰期海浪荷载对结构影响增加,因此需要进一步分析计算结构在浪荷载在下的动态响应情况及疲劳损伤情况;
2)验证了加装锥体结构达到的抗冰效果,但在风荷载、冰荷载耦合作用下风电基础结构是否还能够保证安全,配合其他隔振措施是否能够达到更好的效果,则需要进一步验证分析。
| [1] |
张毅, 马永亮, 曲先强, 等. 冰区海上风机的动力响应及疲劳分析[J]. 舰船科学技术, 2018, 40(1): 81-85. DOI:10.3404/j.issn.1672-7649.2018.01.014 |
| [2] |
刘林, 葛旭波, 张义斌, 等. 我国海上风电发展现状及分析[J]. 能源技术经济, 2012, 24(3): 66-72. |
| [3] |
张宪平. 海上风电发展现状及发展趋势[J]. 电气时代, 2011(3): 46-48. |
| [4] |
刘佰琼, 徐敏, 刘晴. 我国海上风电发展的主要问题及对策建议[J]. 海洋开发与管理, 2015, 32(3): 7-12. DOI:10.3969/j.issn.1005-9857.2015.03.002 |
| [5] |
王译鹤. 冰激窄体结构振动的机理与理论模型研究[D]. 大连: 大连理工大学, 2014.
|
| [6] |
王国军, 张大勇, 王帅飞, 等. 寒区海上风电基础锥体动冰荷载[J]. 科学技术与工程, 2020, .20(31): 12820-12826. |
| [7] |
张大勇, 王国军, 王帅飞, 等. 冰区海上风电基础的抗冰性能分析[J]. 船舶力学, 2018, 22(5): 615-627. |
| [8] |
王帅飞. 冰区风电基础结构抗冰振设计研究[D]. 大连: 大连理工大学, 2020.
|
| [9] |
CLOUGH H F, VINSON T S. Ice forces on fixed conical structures[C]//. Proceedings 142 of the 5th International Offshore Mechanics and Arctic Engineering Symposium, Tokyo, Japan, 1986: 507-514.
|
| [10] |
娄春娟. 近海简易风电基础结构设计研究[D]. 大连: 大连理工大学.
|
| [11] |
Kärnä T, et al. An upper bound model for self-excited vibrations[C]//Proceedings of 19th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), 2007: 177−189.
|
| [12] |
HIRAYAMA K, Obarai. Ice force soninclined structures [C]// Proceeding of the 5th International Offshore Mechanics and Arctic Engineering. Tokyo, Japan, 1986: 515−520.
|
| [13] |
YUE Q J, BI X J. Ice-induced jacket structure vibrations in Bohai Sea[J]. Journal of Cold Regions Engineering, 2001, 14(2): 81−92.
|
| [14] |
Kärnä T, QU Y, KUHNLEIN W. A New spectral method for modeling dynamic ice actions [C]// Proceedings of the 23rd International Conferences on Offshore Mechanics and Arctic Engineering, Vancouver, Canada, 20-25 June 2004. OMAE2004-51360. ASEM 2004: 8−16.
|
| [15] |
欧进萍, 段忠东. 海洋平台结构安全评定: 理论、方法与应用[M]. 北京: 科学出版社, 2003.
|
| [16] |
岳前进, 刘圆, 屈衍, 等. 海洋平台的冰力谱与冰振响应分析[J]. 计算力学学报, 2008, 25(5): 665-670. |
| [17] |
王帅飞, 张大勇, 王国军, 等. 冰致海上风电基础结构稳态振动分析[J]. 船海工程, 2019, 48(6): 91-95. |
| [18] |
季顺迎, 岳前进, 毕祥军. 辽东湾JZ20-2海域海冰参数的概率分布[J]. 海洋工程, 2002, (3): 39−43+84.
|
 2022, Vol. 44
2022, Vol. 44
