新船能效设计指数的提出,促进了船舶能效改进技术的发展,并在船舶设计制造环节采用一切能效改进技术来提升船舶的能效,船舶能效改进技术的不断使用反过来又促进了船舶能效改进技术自身的发展[1]。在这种形势下,船舶风帆助航系统作为船舶航行的辅助动力受到了极大的关注。在船期明确的条件下,在航行过程中,船舶的动力系统可以借助风力助航系统,以便能够降低船舶主机的功率输出,同时借助海面风场提供的推力,降低船舶在航行过程中化石能源的消耗[2]。本文基于智能算法,研究了船舶在风力助航系统下的航线优化设计。
1 船舶风力助航技术 1.1 风速风向测量技术随着近几年科学测量技术的快速发展,风向风速测量技术被广泛地应用到风力助航中,同时随着超声波技术的飞速发展,利用超声波对风速风向进行测量的技术已经在航海船舶、气象监测等领域得到了广泛的应用。时差法是最常用的风速以及风向的测量方法[3]。
以超声波在顺风以及逆风中的传播速度不一致这一特征为基础,对风速以及风向进行测量,该方法称为时差法。基于恒定的距离进行超声波测量的时候,超声波在顺风和逆风中的速度之差主要由测量得到的传播时间差来体现,并且超声波在2个方向上传播的时间差和风速之间的关系是线性的[4]。传播时差的解算方式包括相位差法、频差法以及直接时差法3种。直接时差法是直接计算测量收发时间。频差法是以空气速度与频率变化之间的关系为基础,对风速以及风向进行测量的方法,该方法所得到的测量值更加精确,但是该测量方法受环境影响比较大。相位差测量方法优点在于风场中的温度、速度不会对测量结果产生影响,该方法将时间差转换成相位差之后对风速风向进行计算,相位差测量方法测量精度高,但是成本也高。
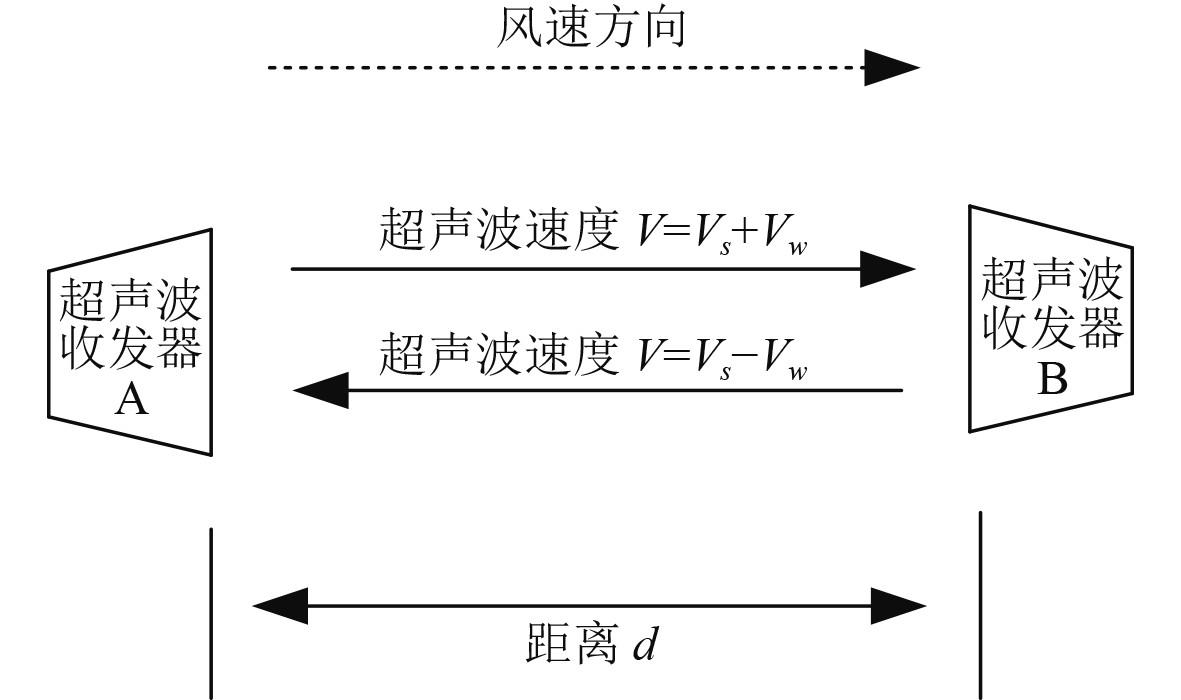
利用时差法进行特定风向测量的时候,测量得到的时间差和风速之间是线性关系,此时可以利用一个收发一体的超声波测量仪,并且将2个探头固定距离安放,方向为东西或者南北方向,2个超声波探头分别向对方发送固定频率的超声波,然后测量2个探头接收到超声波分别需要多长时间,通过这种方法可以求出超声波在逆风以及顺风下的2个传播速度,通过这两个传播速度则可以计算出风速值,其基本原理如图1所示。
|
图 1 一维风速风向测试原理 Fig. 1 Principle of one-dimensional wind speed and direction measurement |
可知,A探头作为发射器,B探头作为接收器,A探头发送固定频率的超声波给B探头,则可以计算出超声波一个方向上的传播时间值;B探头发送固定频率的超声波给A探头,则可以计算出超声波另一个方向上的传播时间值。假定图1中超声波传播的距离恒定为d,风速为VW,超声波逆风传播的时间为t2,超声波顺风传播的时间为t1,则可以得到:
| $ \frac{d}{{{t_1}}} = {V_S} + {V_W}\text{,} $ | (1.1) |
| $ \frac{d}{{{t_2}}} = {V_S} - {V_W}\text{,} $ | (1.2) |
通过式(1)和式(2),则可以推算出:
| $ {V_W} = \frac{d}{2}\left( {\frac{1}{{{t_1}}} - \frac{1}{{{t_2}}}} \right)\text{。} $ | (1.3) |
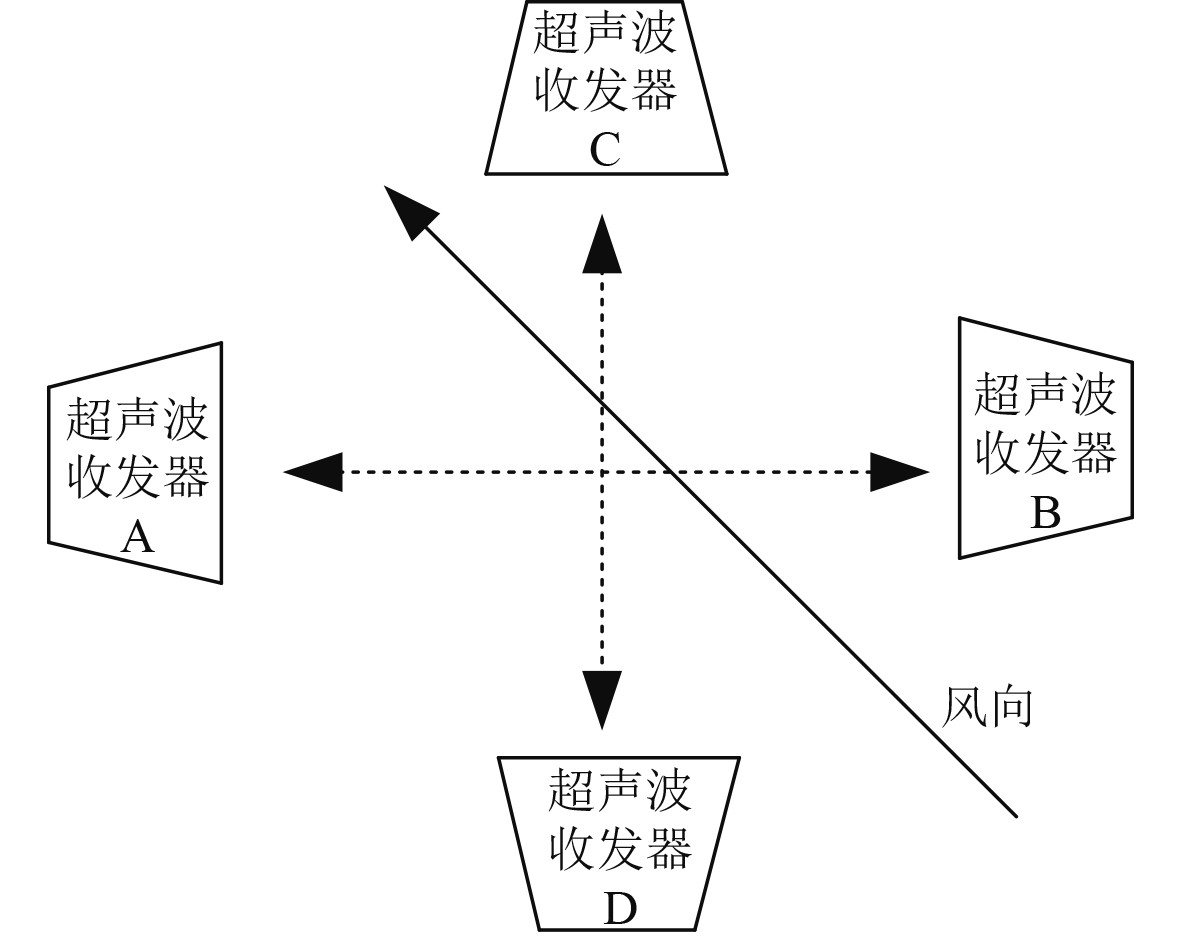
利用上述方法虽然可以计算出风速以及风向,但是只能测量单一方向的风速以及风向,船舶在实际航行环境中,海面上的风速以及风向可以是任意方向,因此上述方法具有局限性,需要进行调整。为了测量船舶航行环境中任意方向上的风速以及风向,可以将2个收发一体的超声波探头进行垂直安放,并且将探头之间的距离固定住,并且测出2个逆风时间以及2个顺风时间,基本原理如图2所示,通过这4个时间则可以求出风速及风向。
|
图 2 二维风速风向测试原理 Fig. 2 Principle of two-dimensional wind speed and direction measurement |
该方法在测量风速以及风向过程中,和超声波的传播速度无关,并且求得的误差小,范围大,可以测量0~360°之间任意方向上的风速,并且该方法在测量过程中由于2对超声波探头之间的距离很短,因此超声波从发射到接收之间的传播时间比较短,这就要求测量系统自身具备高速测量以及高精度处理技术。
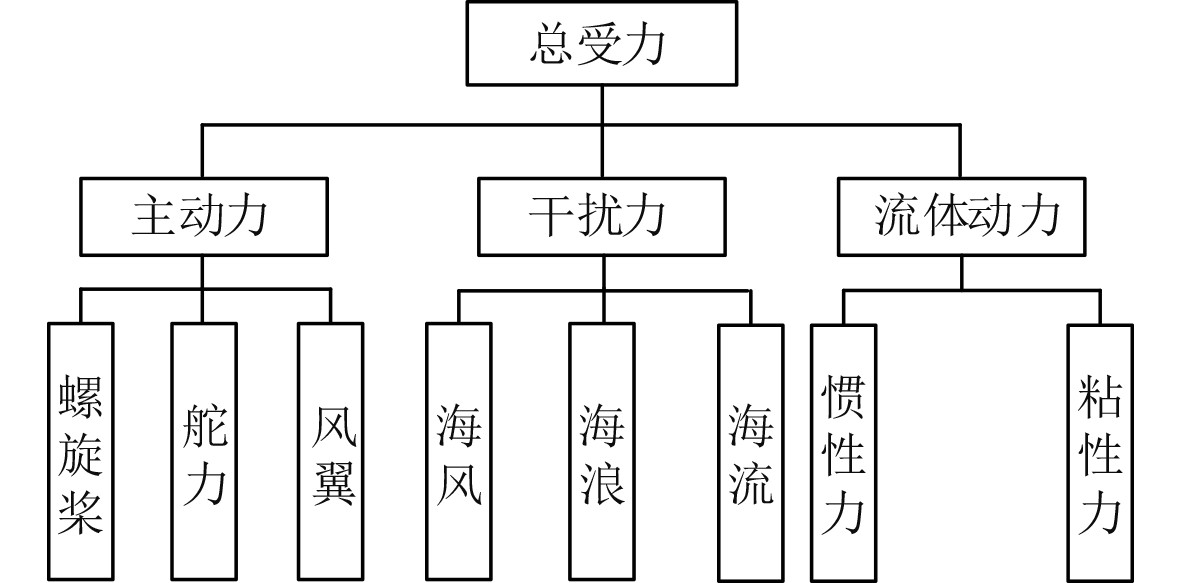
1.2 风力助航船舶运动数学模型船舶在航行过程中的受力分析是以船舶的运动模型为基础的,在海面上航行的船舶主要受到船舶的主动力、周围环境的干扰力以及海水的流体动力3种力的影响,船舶受力结构如图3所示。
|
图 3 风帆助力下船舶受力结构 Fig. 3 Force bearing structure of ship assisted by sail |
基于船舶在海面上航行的受力情况,构建船舶的数学运动模型为:
| $ \left\{\begin{split} & {\left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)vr = {X_H} + {X_P} + {X_R} + {X_C}},\\ & {\left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ur = {Y_H} + {Y_P} + {Y_R} + {Y_C}} ,\\ & {\left( {{I_{pp}} + {J_{pp}}} \right)\dot r = {N_H} + {N_P} + {N_R} + {N_C}} \text{。} \end{split} \right.$ | (1.9) |
风力助航下船舶受到的风翼的助力TW以及侧推力TH可以表示为:
| $ {T_W} = \frac{1}{2}{C_T}{\rho _a}V_a^2{S_W}\text{,} $ | (1.10) |
| $ {T_H} = \frac{1}{2}{C_H}{\rho _a}V_a^2{S_W}\text{。} $ | (1.11) |
式中:CT为推力系数;CH为横向系数;ρa为空气密度;Va为风速;S为风翼面积,并且CT和CH可以用表示为:
| $ \begin{split} & {{C_T} = {C_L}\sin \beta - {C_D}\cos \beta }\text{,} \\ & {{C_H} = {C_L}\cos \beta + {C_D}\sin \beta } \text{。} \end{split}$ | (1.12) |
式中:CL为升力系数;CD为阻力系数,β为风翼角。船舶在升力以及阻力的共同作用下,形成了船舶在航行过程中的风翼助推力,并且船舶上的风翼角β、风向角α以及风翼的回转角φ之间的关系可以表示为:
| $ \varphi {\text{ = }}\alpha {{ - }}\beta \text{。} $ | (1.13) |
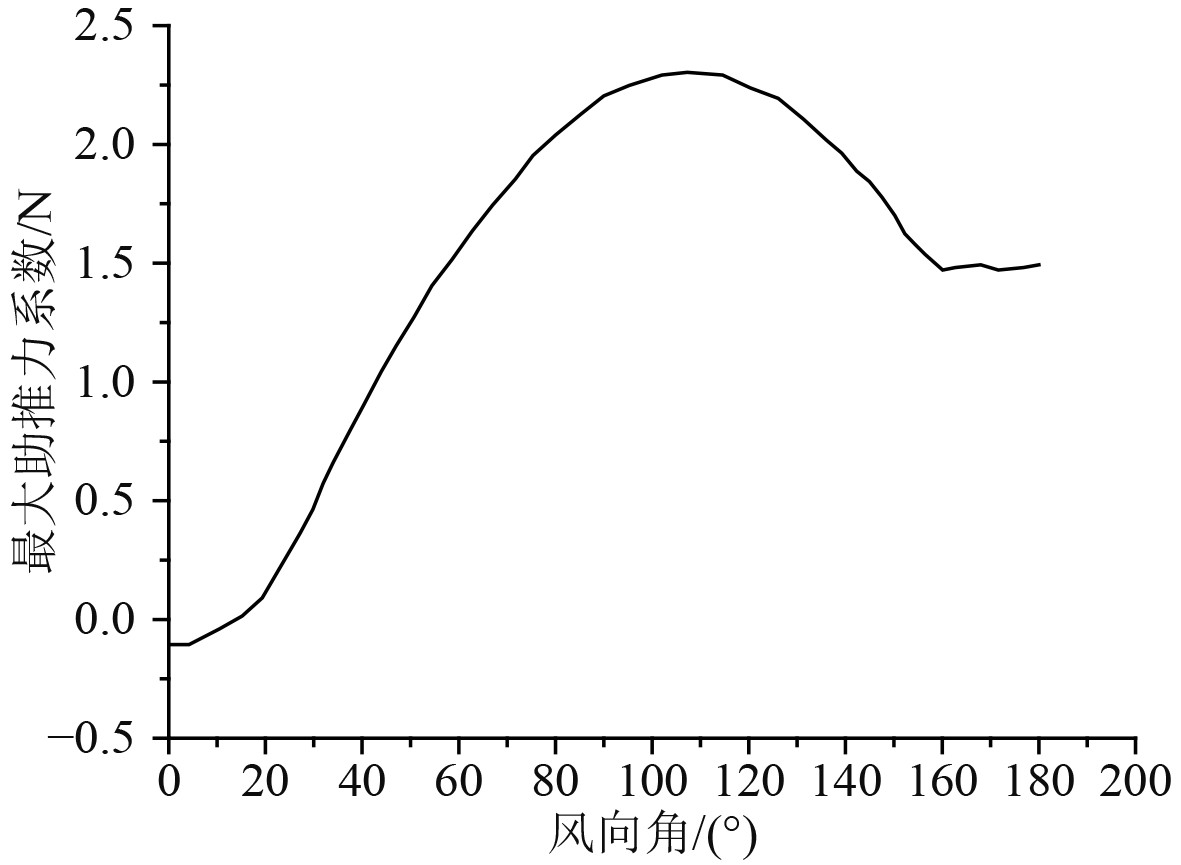
可以看出,当风向角一定时,改变风翼的角度可以对风翼的助推力系数进行调整,因此不同的风向角都会有一个最大的助推力系数与其对应,风向角0°~180°之间的最大推力系数的分析结果如图4所示。可以看出,当风向角大于70°时,可以产生比较大的助推力系数,当风向角为110°的时候,可以产生最大的助推力系数。
|
图 4 最大推助力系数和风向角之间的关系 Fig. 4 Relationship between maximum thrust coefficient and wind direction angle |
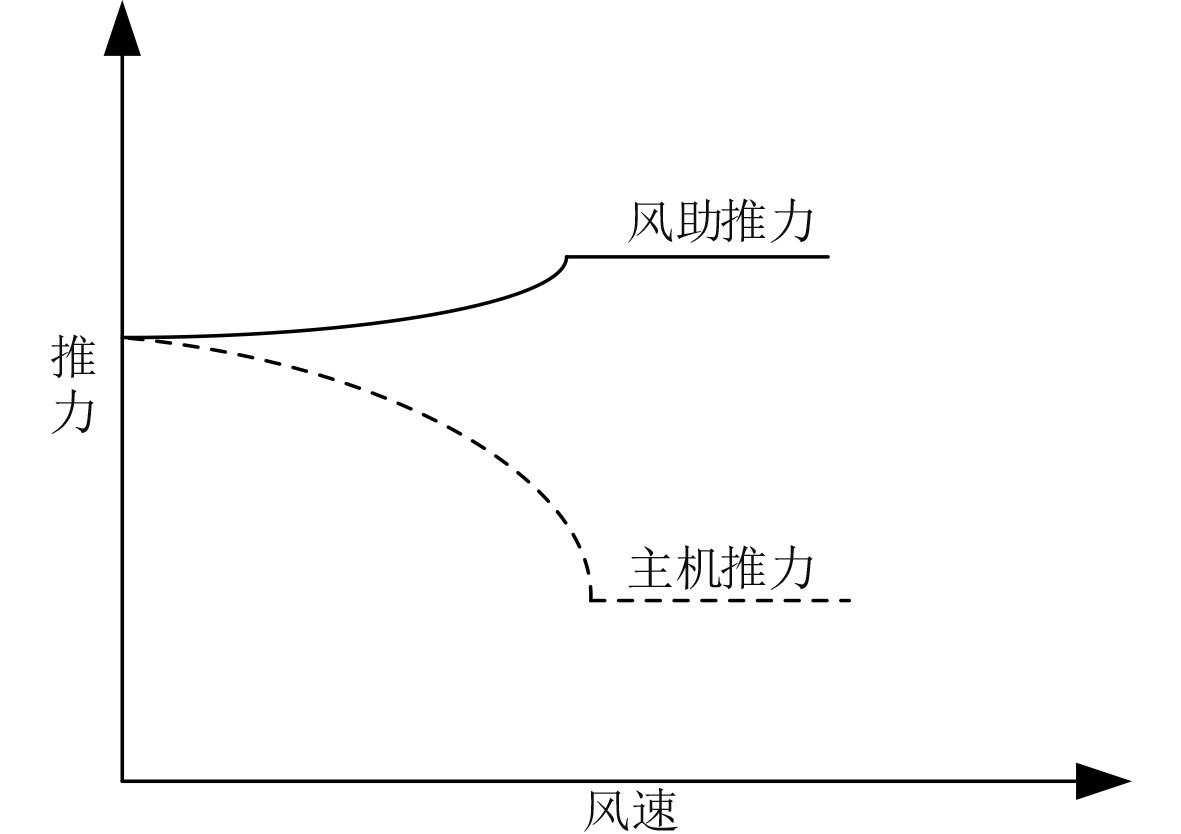
船舶定航速下推力变化示意图如图5所示。可以看出,随着海面风速的增加,风助推力也会增加,但是主机推力会随之降低,并且主机推力在降低到一定程度之后将会维持不变,这是为了确保船舶主机能够正常稳定工作,因为船舶主机的稳定运行需要一个最低负荷,因此船舶的主机推力需要满足下式:
|
图 5 船舶定航速下推力变化示意图 Fig. 5 Schematic diagram of thrust variation of ship at constant speed |
| $ {T_e} \geqslant {T_{\min }}\text{。} $ | (1.14) |
式中,Tmin为船舶主机最低功率对应的推力。
2 船舶航线优化技术 2.1 船舶航线优化智能算法在船舶航行过程中对船舶的航线进行规划,每当对船舶的航路进行调整之后,都会产生一条新的船舶航线,假如f(A)和f(B)分别是新航线以及当前航线的函数值,则可以通过比较f(A)和f(B)的值来确定当前航线是否比新航线更好[5]。本文提出的航线优化算法的目标是对最小的航线函数值进行计算求解,因此当f(A)的值小于f(B)的值的时候,则表示新航线比当前航线更好,因此可以采用最新的航线作为接下来的航线;当f(A)的值大于f(B)的值的时候,则表示新航线比当前航线差,即新航线为劣航线,但是并不意味着直接将新航线丢弃,而是根据一定的标准进行再次判断,同时对劣航线进行部分保留,这种方法可以防止船舶的航线优化算法过早地收敛,并且可以使得船舶航线变得多样,增加了船舶航线靠近最优航线的概率,是否能够采用劣航线则需要使用Metropolis准则进行判断。
Metropolis准则在模拟退火算法中可以判断当前解能否移向新解,因此可以采用该方法对劣航线进行取舍判断。假设xi为船舶当前航线,其目标函数值为f(xi),xj为船舶新航线,其目标函数值为f(xj),则新航线用做最优航线的概率Pt计算公式为:
| $ {P_t} = \left\{ {\begin{array}{*{20}{c}} 1,&{f\left( {{x_i}} \right) > f\left( {{x_j}} \right)}\text{,} \\ {\exp \left( { - \dfrac{{f\left( {{x_i}} \right) - f\left( {{x_j}} \right)}}{t}} \right)},&{f\left( {{x_i}} \right) < f\left( {{x_j}} \right)} \text{。} \end{array}} \right. $ | (2.1) |
式中,t为退火算法中的温度参数。在对船舶的新航线进行判断的过程中,算法系统会随机产生一个数σϵ(0,1]。假如Pt
基于Metropolis准则的船舶最优航线算法在一开始的时候,由于温度系数t的值比较大,因此接收新航线的概率值比较高,因此更容易接收劣航线,此时可以跳出局部在全局寻找最优的可能性;随着温度系数t的逐渐变小,劣航线越来越难被接收,此时跳出局部的难度也逐渐变大[6]。因此采用本文的算法在进行船舶航线优化的过程中,如果想得到最优的全局解,则需要在温度系数t较高的时候进行大量的全局搜索,在温度系数t较低时进行局部搜索,这样则可以尽可能地接近全局最优解。
2.2 最优航线模型对船舶进行航线优化,船舶不但可以避开有害的风浪,降低船舶失速的危险性,同时可以利用海面上的风作为辅助动力,这样可以使得船舶的速度在恒定的情况下,最大化地降低船舶主机的功率,最终达到降低船舶燃油消耗的目标[7],船舶在海面上航行过程中的燃油消耗总量、主机的输出力以及船舶航行总距离之间的关系表示为:
| $ {W_e} = \sum\limits_{i = 1}^{N - 1} {{{\left( {{T_e}} \right)}_i} \cdot {S_i}} \text{。} $ | (2.2) |
式中:We为船舶总耗能;Te为船舶主机推力;N为船舶航线上的航路数;i为第i段航路;Si为第i段航路的距离。
当船舶的航速恒定时,船舶主机的推力Te,海风提供的助力Tw以及船舶航行过程中的阻力R三者之间的关系表示为:
| $ R = {T_e} + {T_w}\text{。} $ | (2.3) |
可以得出,船舶在航行过程中的总的燃油消耗量可以表示为:
| $ {W_e} = \sum\limits_{i = 1}^{N - 1} {\left( {{R_i} - {{\left( {{T_w}} \right)}_i}} \right) \cdot {S_i}} \text{。} $ | (2.4) |
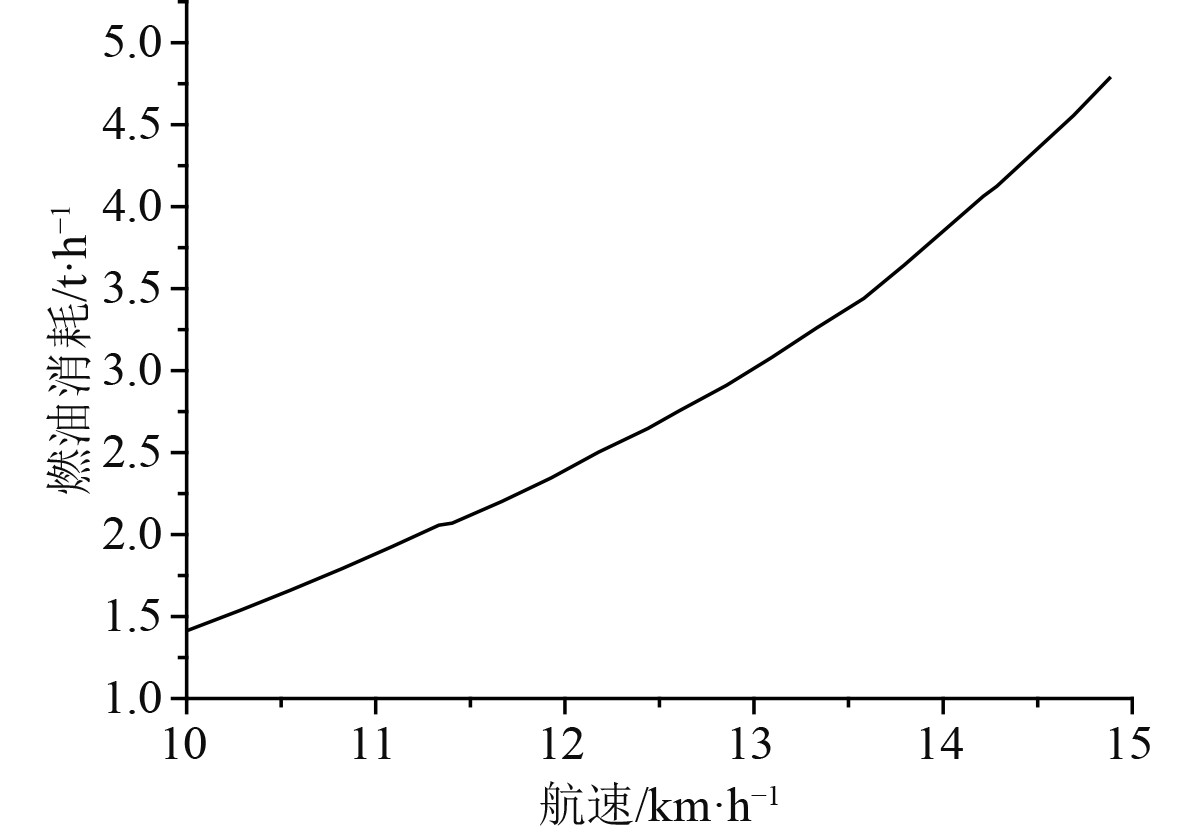
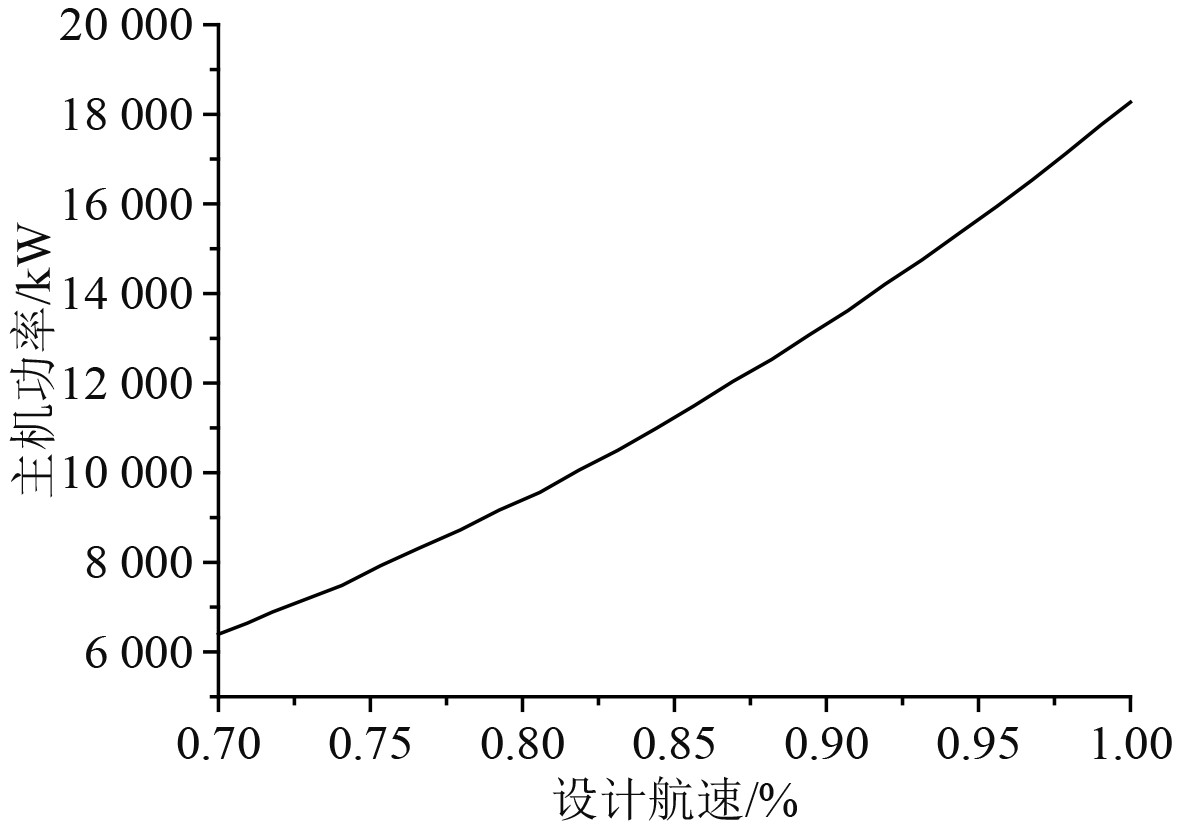
可以看出,在船舶速度一定的情况下,如果船舶的航程不会增加太多,则可以通过适当的绕航,不断调整船舶主机的输出功率以及海风提供的辅助推力,尽可能地得到最小的船舶主机功率,最终使得船舶的燃油消耗最小,燃油消耗和航速之间的关系如图6所示,船舶设计航速和主机输出功率之间的关系如图7所示。
|
图 6 燃油消耗和航速之间的关系 Fig. 6 Relationship between fuel consumption and speed |
|
图 7 船舶设计航速和主机输出功率之间的关系 Fig. 7 Relationship between ship design speed and main engine output power |
在船舶运输过程中,如何降低能源消耗、提升经济效益,使得船舶实现节能减排的目标,已经成为船舶工业面临的重要问题。
| [1] |
金世国, 闰冰. 风力助航在船舶航行中的优化建模研究[J]. 舰船科学技术, 2016, 38(12): 46-48. |
| [2] |
计明军, 陈哲, 王清斌. 集装箱船舶支线运输航线优化算法[J]. 交通运输工程学报, 2011, 11(4): 68-75. |
| [3] |
李元奎, 张英俊, 岳兴旺, 等. 面向风帆助航的海洋风力资源分析方法[J]. 中国航海, 2013, 36(3): 90-94. |
| [4] |
袁志涛, 刘克中, 余庆, 等. 面向海上风电工程的船舶助航系统设计与实现[J]. 船舶工程, 2021, 43(S1): 156-160. |
| [5] |
陈淦. 基于云计算的海洋风场对船舶航线影响模型研究[J]. 舰船科学技术, 2017, 39(16): 43-45. |
| [6] |
胡以怀, 袁春旺. 海上航线风能资源的调查与分析[J]. 中国航海, 2018, 41(2): 107-112. |
| [7] |
何建海, 胡以怀, 张建霞, 等. 风能在船舶上的应用现状及展望[J]. 船舶工程, 2013, 35(5): 112-115. |
 2022, Vol. 44
2022, Vol. 44
