通常条件下,舰船由起始点至目标点间存在多条不同航线供选择[1]。但考虑舰船实际航行过程中受障碍物、天气因素、地理环境因素等不同因素影响,不同航线的航行风险以及航程成本存在一定差异性[2]。因此,在已知航线内选取最佳航线成本舰船经营公司以及舰船航行过程中掌控者所面临的关键问题。
韩志豪等[3]在舰船航线研究问题中引入深度强化学习方法,利用电子海图拟合航道,通过深度强化学习方法生成获取最优航线。该方法以拟合航道为基础,未考虑舰船实际运行中的天气因素,导致最终所选航线中存在一定风险。吕进锋等[4]在航线选取问题中采用随机路径图方法生成初始航线,在此基础上通过和声算法优化航线。该方法实际应用过程中需要进行大量运算,过程较为复杂。
针对上述方法中存在的问题,提出应用数据挖掘技术的舰船最佳航线自动选取方法,通过该研究保障舰船航行安全,降低航行成本。
1 舰船最佳航线自动选取方法舰船最佳航线选取中的“最佳”包括风险最低、航程最短、能耗最低、用时最少等内容,其中航程对于能耗与用时产生直接影响。因此在选取舰船最佳航线过程中应着重考虑航线的风险与航程。
1.1 舰船航线风险评估 1.1.1 风险评估指标体系构建采用数据挖掘技术中的模糊评估方法评估各航线的航行风险。舰船航线风险评估过程中评估指标的合理性与代表性对于舰船航线风险评估结果的准确性与科学性产生直接影响。由于舰船航行过程中周边环境具有复杂多变性特征,因此,对舰船航线产生威胁的因素也较多。考虑舰船航线风险评估指数数据的可取性,依照舰船航行的实际情况,确定主要指标构建舰船航线风险评估指标体系,如表1所示。
|
|
表 1 舰船航线风险评估指标体系构建 Tab.1 Construction of ship route risk assessment index system |
对表1内各舰船航线风险评估指标实施量化处理能够更直观地描述各指标的属性与特征。依照实际情况对表1内各指标实施量化处理。
1)A11:其值可通过航线区域的天气预报数据获取,用于描述冰的密集度对于舰船航行的威胁程度,同舰船航线风险之间呈正比例相关。
2)A12:用于描述舰船航线内冰密集度低于40%的天数,其值同舰船航线风险之间呈反比例相关。A12的量化描述为:
| $ A12{\text{ = }}\frac{B}{{{B_{all}}}} \times \phi。$ | (1) |
式中:
3)A13:用于描述低能见度对舰船航线的威胁程度,其值同舰船航线风险之间呈正比例相关。A13量化描述为:
| $ A13{\text{ = }}\left( {\frac{{{Z_0}}}{Z}} \right) \times \left( {\frac{{{X_n}}}{Y}} \right) 。$ | (2) |
式中:
4)A14:用于描述大风对舰船航线的威胁程度,其值同舰船航线风险之间呈正比例相关。A14的量化描述为:
| $ A14{\text{ = }}\left( {\frac{W}{{{W_{\min }}}}} \right)\left( {\frac{{{X_f}}}{Y}} \right) 。$ | (3) |
式中:
5)A15:用于描述气温对舰船航线的威胁程度,其值同舰船航线风险之间呈反比例相关。A15的量化描述为:
| $ A15=\left\{\begin{array}{*{20}{l}}0&Q > 0^{\circ}C,\\ \left|\dfrac{Q}{0-{Q}_{\mathrm{min}}}\right|&Q\leqslant 0^{\circ}C。\end{array}\right.$ | (4) |
式中:
6)A21:用于描述航道水深对航行舰船的威胁程度,该值同舰船航行过程中触礁与搁浅的风险之间呈反比例相关。A21的量化描述为:
| $ A21 = \left\{ \begin{array}{*{20}{l}} 0& \dfrac{{Num\left( {{d_h} \geqslant E} \right)}}{{Num\left( {all} \right)}} \geqslant 0.6,\\ 1 - \dfrac{D}{E}&0 < \dfrac{{Num\left( {{d_h} \geqslant E} \right)}}{{Num\left( {all} \right)}} < 0.6 。\end{array} \right. $ | (5) |
式中:
7)A22:用于描述航道宽度对航行舰船的威胁程度,其值同舰船航线风险之间呈反比例相关。A22的量化描述为:
| $ A22 = \left\{ \begin{aligned} &0&{w_h} \geqslant H ,\\ &1 - \frac{{{w_h}}}{H} & 0 \leqslant {w_h} < H 。\end{aligned} \right. $ | (6) |
式中:
8)A23:用于描述航道周边岛屿对航行舰船的威胁程度,其值同舰船航线风险之间呈正比例相关。A23的量化描述为:
| $ A23 = \frac{{{M_d}}}{M} \times \phi 。$ | (7) |
式中:
9)A24:用于描述暗礁对航行舰船的威胁程度,其值同舰船航线风险之间呈正比例相关。A24的量化描述为:
| $ A24 = \frac{{{M_a}}}{M} \times \phi。$ | (8) |
式中:
采用模糊评估方法评估舰船航线风险,公式描述如下:
| $ {K_i} = {W_i} \times {R_i} 。$ | (9) |
式中:
依照上述模型获取舰船航线风险评估的模糊综合评估模型:
| $ K = W \times R 。$ | (10) |
依照式(10)对权向量计算确定最终舰船航线风险评估结果,以
| $ v = \frac{{\displaystyle\sum\limits_{j = 1}^m {{k_j}{v_j}} }}{{\displaystyle\sum\limits_{j = 1}^m {{k_j}} }} 。$ | (11) |
通过上述过程能够在舰船航线中风险较高的航线去除,得到风险较低的航线。
1.2 基于A*算法的航程最短航线确定以一个交通网络描述风险等级为中等及以下的航线,利用无向图
若存在路径
| $ l\left( {{o_i},{o_j}} \right) = l\left( {{o_i},{o_k}} \right) + l\left( {{o_k},{o_j}} \right) 。$ | (12) |
由此可知,舰船航行的起始点与目标点间最短航程
| $ \min L = \sum\limits_{{o_i},{o_j} \in {p^ * }} {\left( {{o_i},{o_j}} \right)} 。$ | (13) |
采用启发式搜索算法A*算法在低风险航线中搜索最短航程,通过估价函数
由此获取低风险航线中最短航程的航线,也就是舰船最佳航线。
2 应用结果 2.1 应用对象相关信息图1为应用对象的航行区域。
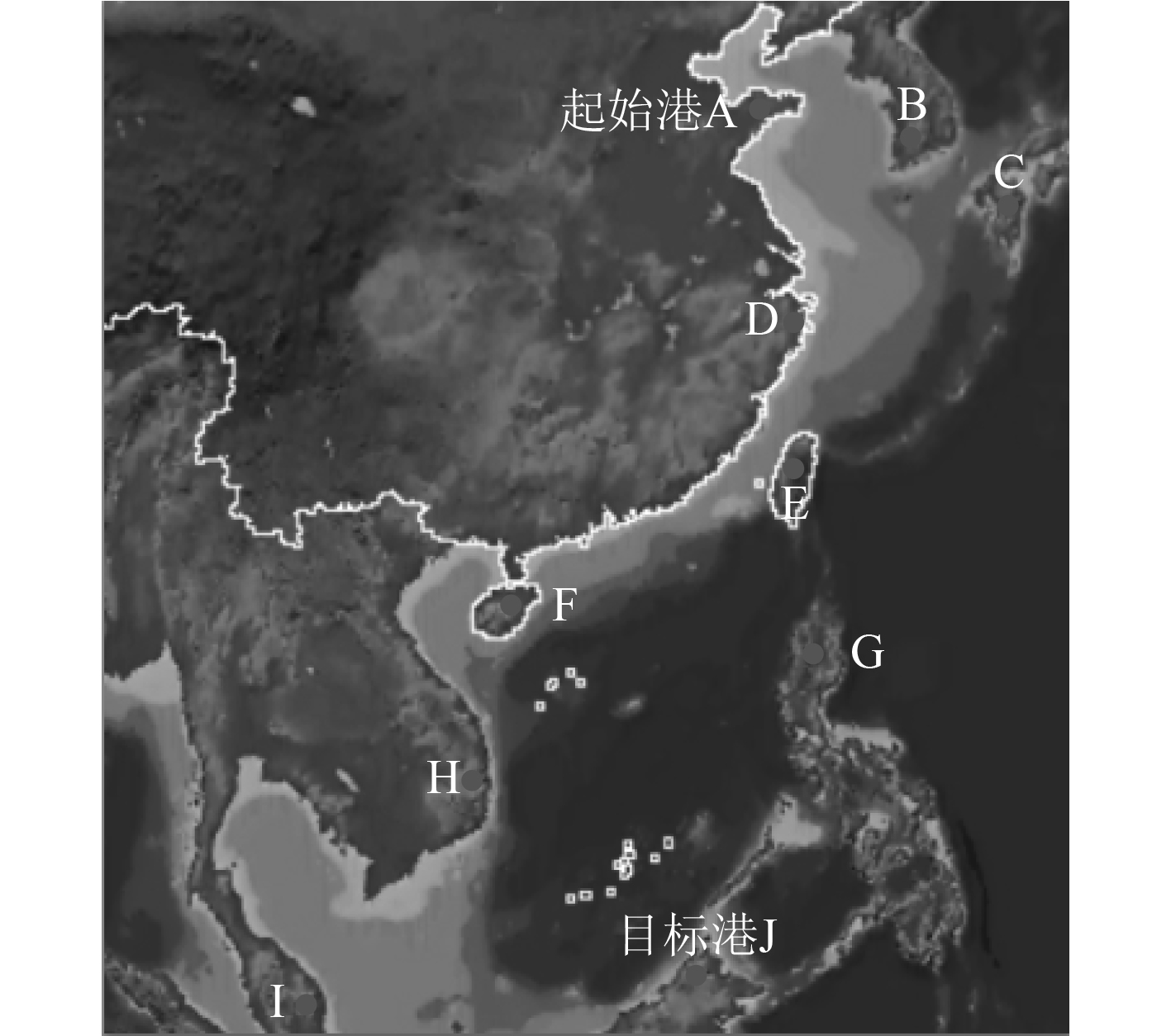
|
图 1 应用对象航行区域 Fig. 1 Navigation area of application object |
图2为舰船航线风险评估中天气因素与地理环境因素的指标权重。
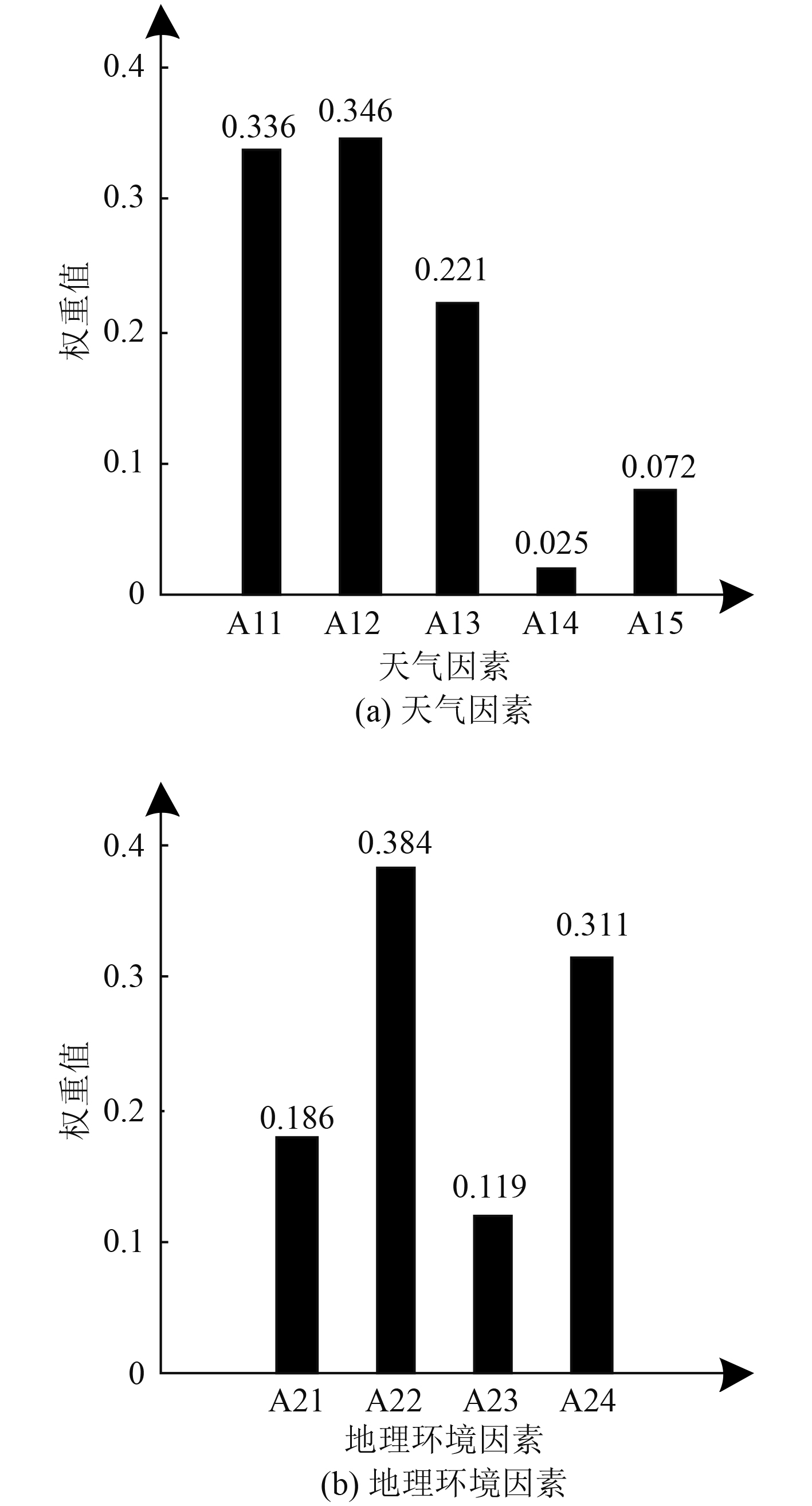
|
图 2 舰船航线风险评估指标权重计算结果 Fig. 2 Calculation results of weight of ship route risk assessment index |
分析可知,在天气因素内,A12指标的权重最大,其次为A11指标,这2个指标均同冰况相关,由此说明冰况是影响应用对象安全航行的最主要原因。同时A13的指标权重也较大,说明应用对象在实际航行过程中需注意能见度对于航行安全的影响。A13指标与A15指标的权重值均为超过0.1,由此说明应用对象在实际航行过程中受气温因素与大风因素的影响较为微弱。在地理环境因素内,A22指标与A24指标的权重值均高于0.3,由此说明这2个指标对应用对象安全航行的影响较为显著,而A21指标与A23指标的权重较小,说明这2个指标对应用对象安全航行不会造成较大风险。
2.3 实际应用测试采用本文方法选取舰船航线的最终目的是保障舰船航线安全,并最大限度上节省舰船航行时间与能源消耗。对比采用本文方法前后,应用对象航行过程中的事故发生率以及航行时间与能源(柴油)消耗等情况,结果如表2所示。
|
|
表 2 应用对象事故发生率航行时间等对比结果 Tab.2 Comparison results of accident rate and sailing time of application object |
分析可知,应用对象利用本文方法选取航线后,在航行过程中事故发生率、航行时间以及能源消耗量均呈现显著下降趋势,由此说明本文方法能够有效保障应用对象航行安全,降低应用对相关航行时间与能源消耗,达到最初研究目的。
3 结 语本文研究应用数据挖掘技术的舰船最佳航线自动选取方法,以确保舰船焊缝过程中的低风险与最短航程为目标,利用数据挖掘技术中的模糊评估法和A*算法获取最佳航线。应用结果显示本文方法能够有效降低舰船航行的事故发生率、航行时间以及能源消耗量。
| [1] |
徐振烊, 张静远, 王鹏. 水下地形辅助导航中匹配航路的选取[J]. 系统工程与电子技术, 2019, 41(11): 2588-2596. |
| [2] |
王莉莉, 蒋一森. 基于航程加权的航路网络效能仿真分析[J]. 计算机仿真, 2019, 36(6): 120-124+159. DOI:10.3969/j.issn.1006-9348.2019.06.024 |
| [3] |
韩志豪, 汪益兵, 张宇, 等. 基于深度强化学习的船舶航线自动规划[J]. 中国航海, 2021, 44(1): 100-105. DOI:10.3969/j.issn.1000-4653.2021.01.017 |
| [4] |
吕进锋, 马建伟, 李晓静. 基于改进的随机路径图及和声算法的舰船航线规划[J]. 控制理论与应用, 2020, 37(12): 2551-2559. |
 2022, Vol. 44
2022, Vol. 44
