对船舶在随机海浪中的横摇运动进行预测并应用此预测信号对船舶或船舶稳定平台进行预测控制,从而解决船舶稳定平台的控制滞后问题,使船舶稳定平台控制系统更加精准。
1 随机海浪和船舶横摇模型船舶一般是在随机海浪下工作,因此需通过研究随机海浪的运动情况来建立船舶横摇运动模型。本文建立随机海浪的仿真模型,产生海浪波倾角信号,以此为基础建立船舶横摇模型,并在3级海况下对船舶横摇进行仿真分析。
1.1 随机海浪模型在实际情况中,通常通过分析海浪波能谱对海浪的真实情况进行研究。为反映海浪的能量密度,常用海浪波能谱进行表示,其中海浪波能谱有3种分别是:Pierson-Moscowitz谱(P-M谱)、ITTC双参数波谱和JONSWAP波谱[1]。在随机海浪建模中应用P-M谱,其函数表达式为:
| $ S(\omega ) = \frac{{ A}}{{{\omega ^5}}}\exp \left( - \frac{B}{{{\omega ^4}}}\right)。$ | (1.1) |
其中:
波倾角能量谱密度函数
| $ \zeta (t){\text{ = }} \sum\limits_{i = 1}^\infty {\sqrt {2Sa({\omega _i})\Delta {\omega _i}} } \cos ({\omega _i}t + {\varepsilon _i}),$ | (1.2) |
其中
海浪的最大有效波倾角
| $ {\alpha _0}{{(t) = }} \frac{{{\omega ^2}}}{g}\sum\limits_{i = 1}^\infty {\sqrt {2Sa({\omega _i})\Delta {\omega _i}} } \cos ({\omega _i}t + {\varepsilon _i})。$ | (1.3) |
但因海上实际情况复杂多变,在实际船舶航行中,船舶波倾角会因海上天气情况、船舶的载重量以及船舶的型号而产生影响,因此关于真实的船舶波倾角还需对式(3)进行修正。海浪的有效波倾角
| $ {{\textit{K}}_{\text{1}}}{\text{ = }}\exp \left( - \frac{{kd}}{2}\right),$ | (1.4) |
| $ {{\textit{K}}_{\text{2}}}{\text{ = }}1{ - }\sqrt {{C_W}{{\left(\frac{B}{\lambda }\right)}^2}}。$ | (1.5) |
其中:
| $ {\alpha _{e0}}{\textit{(t)}}= {{\textit{K}}_{\text{1}}}{{\textit{K}}_{\text{2}}}{\alpha _0} = {{\textit{K}}_{\text{1}}}{{\textit{K}}_{\text{2}}}\frac{{{\omega ^2}}}{g}\sum\limits_{i = 1}^\infty {\sqrt {2Sa({\omega _i})\Delta {\omega _i}} } \cos ({\omega _{ei}}t + {\varepsilon _i})。$ | (1.6) |
在船舶的实际航行中,可根据随机海浪对船舶的波倾角及有效波倾角进行仿真。根据式(6)使用Matlab软件,在3级海况下即有义波高为4 m,航速为6 m/s,航向为90°时,对海浪波能谱、海浪波倾角和有效波倾角进行仿真,仿真结果如图1和图2所示。
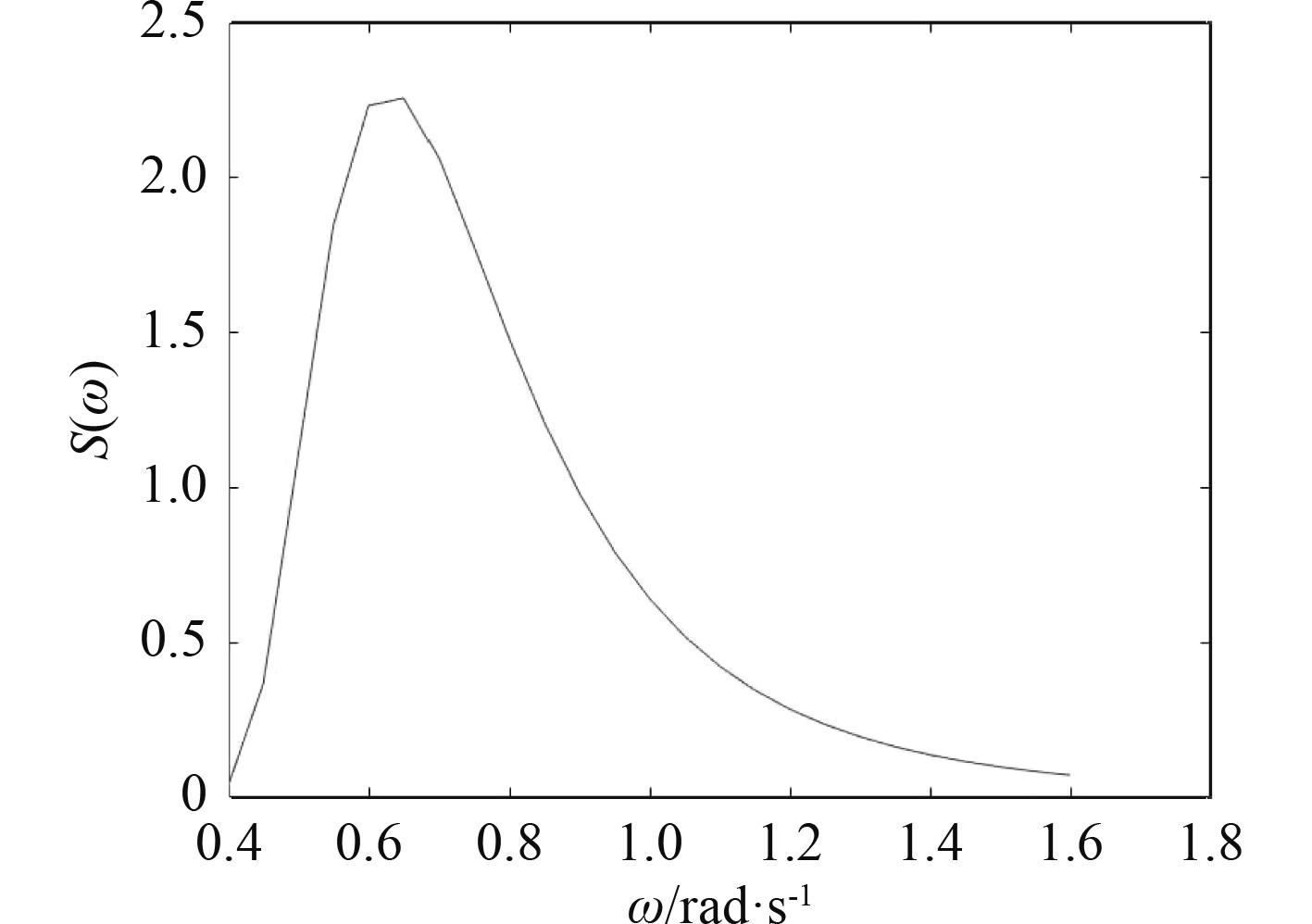
|
图 1 海浪波能谱 Fig. 1 Wave energy spectrum of ocean waves |

|
图 2 海浪波倾角 Fig. 2 Wave inclination angle |
根据Conolly理论以及对船舶在横摇时的某一时刻位置进行船体的受力分析,船舶横摇运动受惯性力矩、恢复力矩、阻力力矩和海浪扰动力矩共同作用,经平衡原理所受力矩总和为0才能使船保持平衡,则其运动力学方程如下[3]:
| $ ({J_\theta }{\text{ + }}\Delta {J_\theta })\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{t^2}}} + 2{N_\theta }\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} + Dh\theta = {M_\theta }。$ | (1.7) |
其中:
| $ {M_\theta } = \Delta {J_\theta }\frac{{{{\rm{d}}^2}{\alpha _{e0}}}}{{{\rm{d}}{t^2}}} + 2{N_\theta }\frac{{{\rm{d}}{\alpha _{e0}}}}{{{\rm{d}}t}} + Dh{\alpha _{e0}},$ | (1.8) |
将式(8)代入式(7)中并进行相应的拉式变换,可得到船舶横摇角
| $ G(s) = \frac{{\theta (s)}}{{{\alpha _{e0}}(s)}} = \frac{{{\omega _\theta }^2\left(\dfrac{{\Delta {J_\theta }}}{{Dh}}{s^2} + \dfrac{{2{\zeta _\theta }}}{{{\omega _\theta }}}s + 1\right)}}{{{s^2} + 2{\zeta _\theta }{\omega _\theta }s + {\omega _\theta }^2}}。$ | (1.9) |
其中:
依据上述横摇模型,利用Matlab工具就能得出船舶横摇运动仿真曲线,其运动曲线如图3所示。
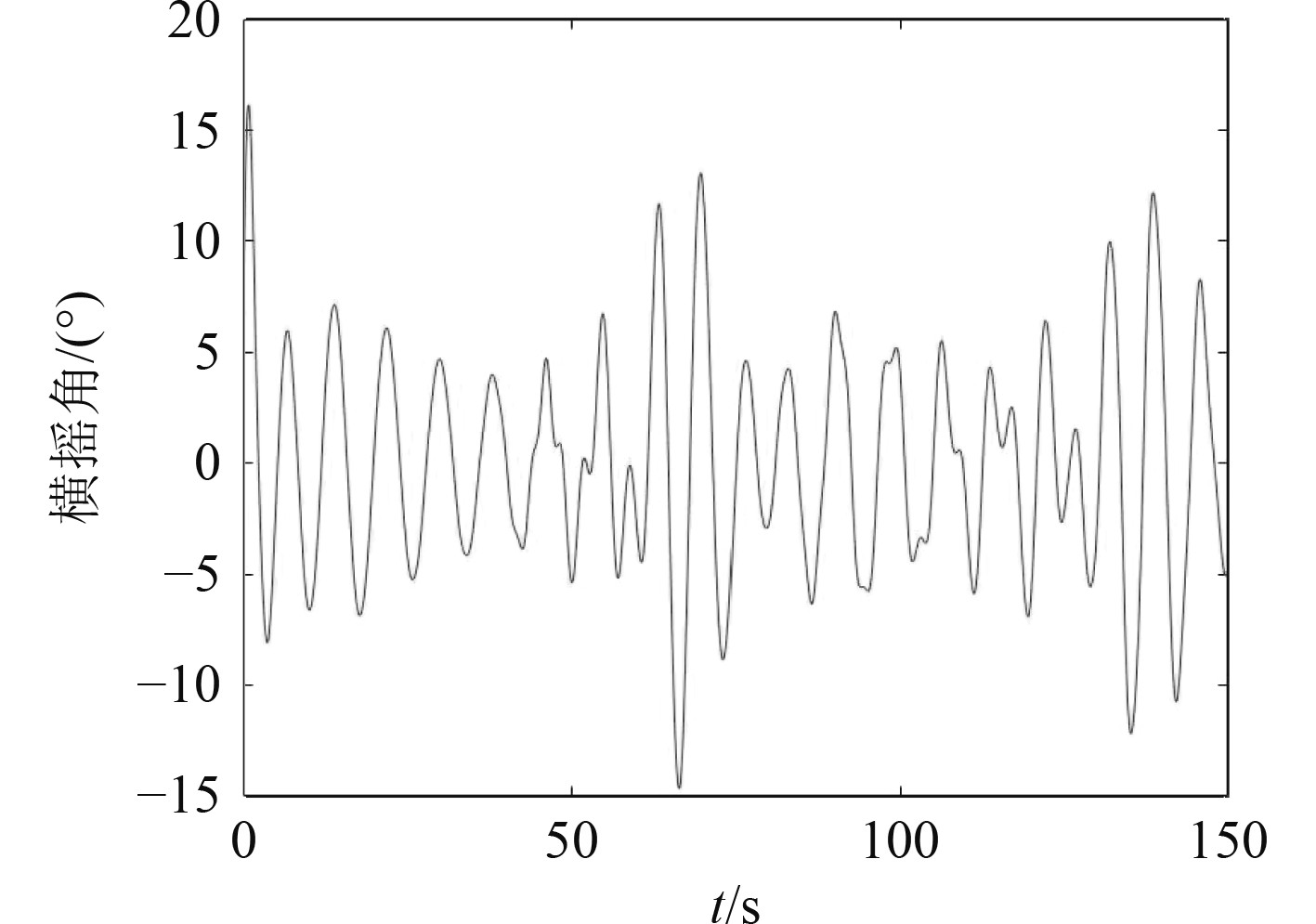
|
图 3 船舶横摇角 Fig. 3 Ship roll angle |
针对船舶运动的预测建模的主要方法有:卡尔曼滤波法、时间序列分析法、机器学习方法、灰色理论等方法,本文采用机器学习混合模型,应用BP神经网络和随机森林混合预测方法,对船舶的横摇运动进行预测分析[4]。
2.1 BP神经网络预测BP神经网络作为当下广泛应用的神经网络模型之一,是一种通过误差逆传播算法训练的多层前馈网络。应用最速下降法作为其学习规则,在训练时权值和阈值会通过反向传播不断调整促使得到最小的网络的误差平方和[5]。针对BP神经网络预测,本文选取1500个船舶横摇随时间变化的历史数据,其中训练集用前1000个数据作为样本,测试集用后500个数据作为样本。其预测仿真结果如图4所示。
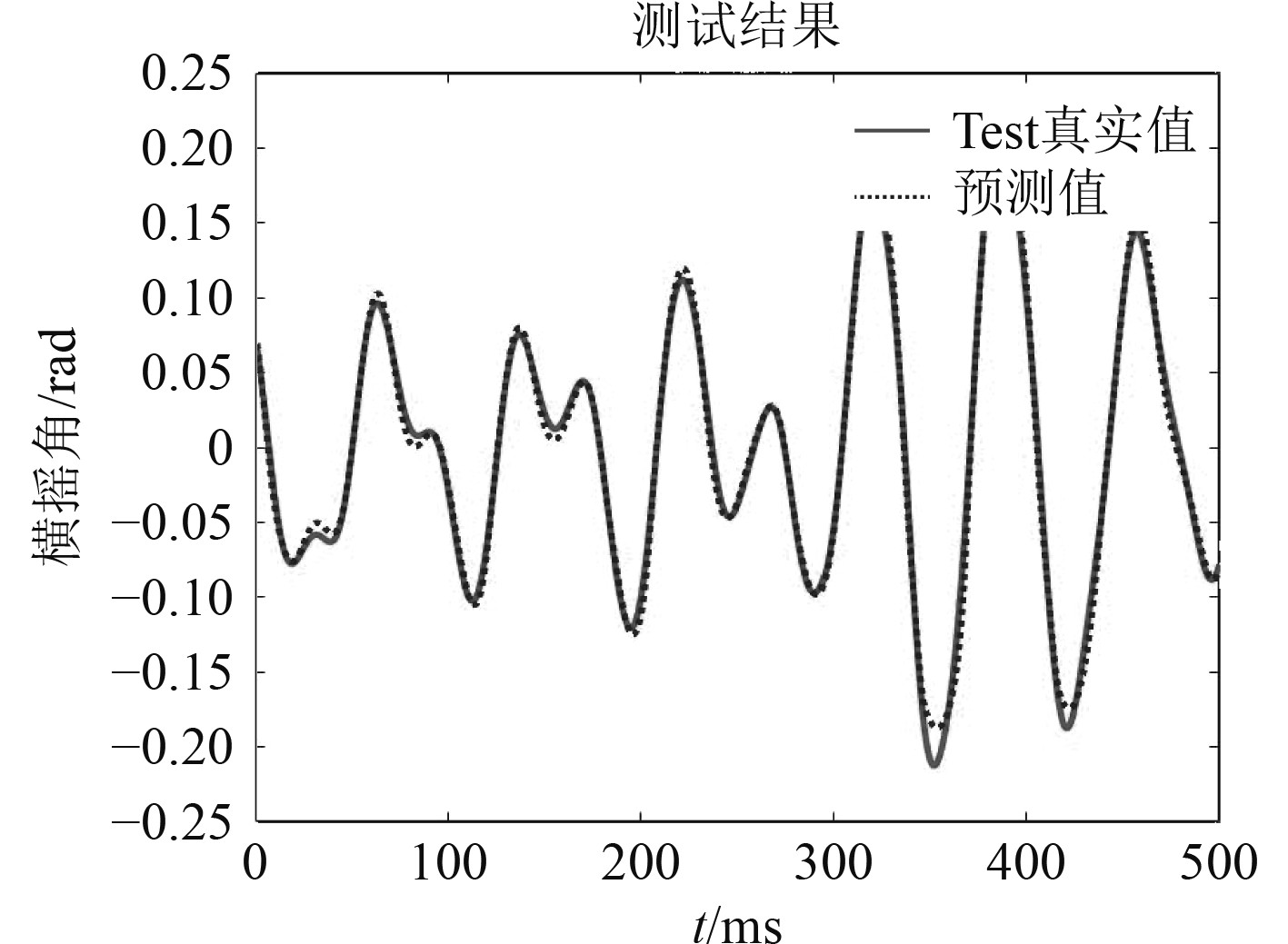
|
图 4 BP神经网络预测 Fig. 4 BP neural network prediction |
随机森林(RF)作为统计学习理论的一种,它在原始样本中抽取多个样本的方法是应用bootsrap重抽样方法并对每个样本进行决策树建模,建模后通过组合多棵决策树来进行预测,最后以投票的方式得到最终预测[6]。因对噪声和异常值有较强的容忍度并且不易出现过度拟合情况,所以预测准确率较高。同上述BP神经网络预测模型选取样本方式相同,其预测仿真结果如图5所示。
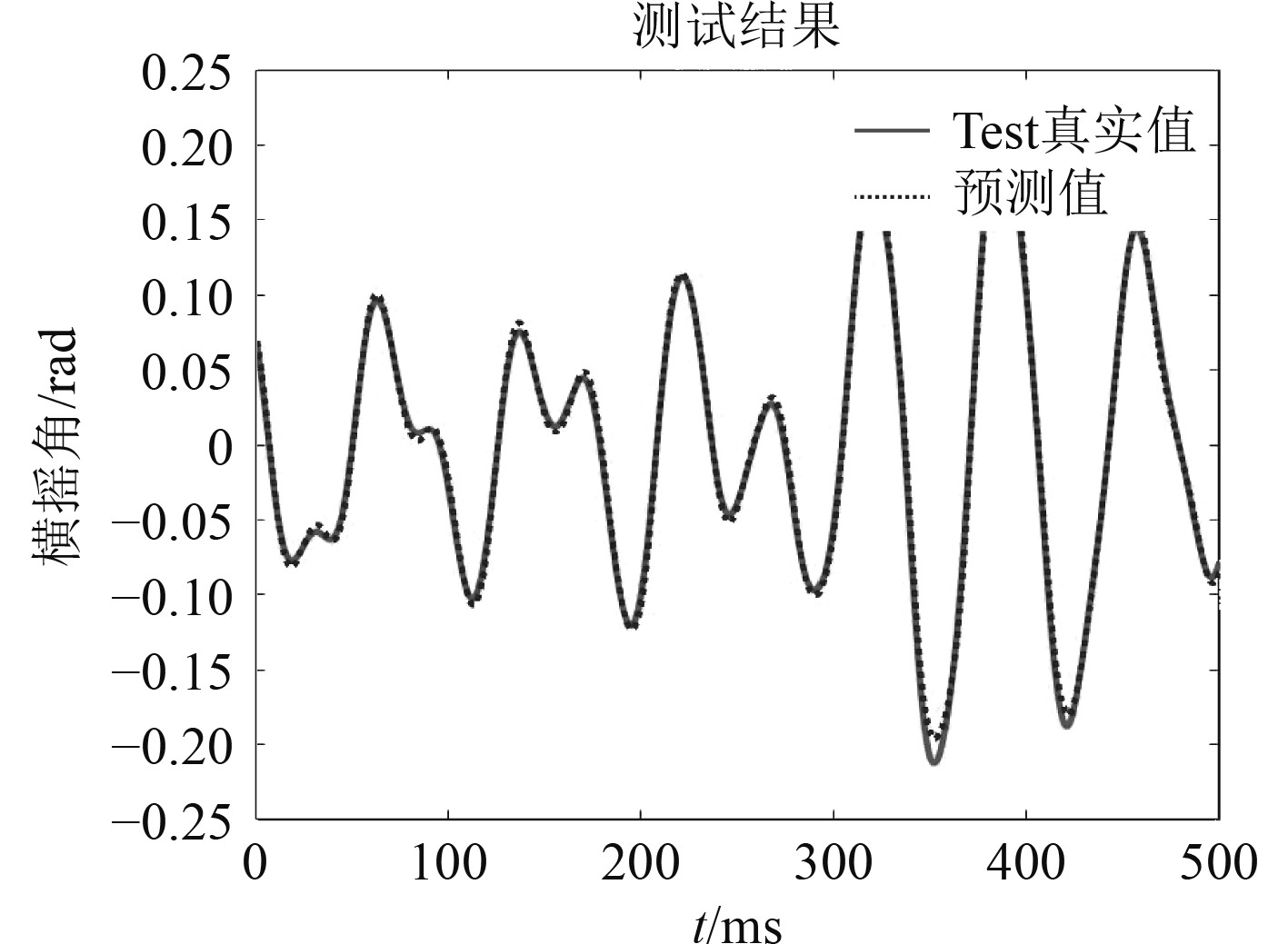
|
图 5 随机森林预测 Fig. 5 Random forest prediction |
在上述算法中,由于BP神经网络受参数选择的影响较为明显,且计算结果受到其初始权值的影响,容易过拟合或者欠拟合,同时样本较少时难以达到较好的效果[7]。随机森林等算法也在不同的具体问题上优势发挥不同,如设置不同的随机森林参数会有不同的效果。由于单一模型可以只能在预测的某一种趋势上效果较好,为了能够获得更好的预测效果,采用多种模型加权线性叠加的方法来组合成更为精确的模型[8]。
上述2种模型的预测结果分别为:
| $ \begin{split} & {y_1}(x) = func1(x),\\ & {y_2}(x) = func2(x)。\end{split}$ | (2.1) |
本文构造一种加权矩阵
| $ yC{\text{omb}}(x){\text{ = }}\sum\limits_{i = 1}^2 {w(i)yi(x)},$ | (2.2) |
其中
| $ \sum\limits_{i = 1}^2 {w(i)} {\text{ = 1}}。$ | (2.3) |
为选出一组最佳的加权参数,从而使预测误差最小,构造优化的目标函数如下:
| $ {\min }\;\;E{\text{mse = }}\dfrac{1}{m}\displaystyle\sum\limits_{k = 1}^m \left[\displaystyle\sum\limits_{i = 1}^n w(i)yi(x{\rm{cross}}^k) - y{\rm{real}}(x{\rm{cross}}^k)\right]^2。$ | (2.4) |
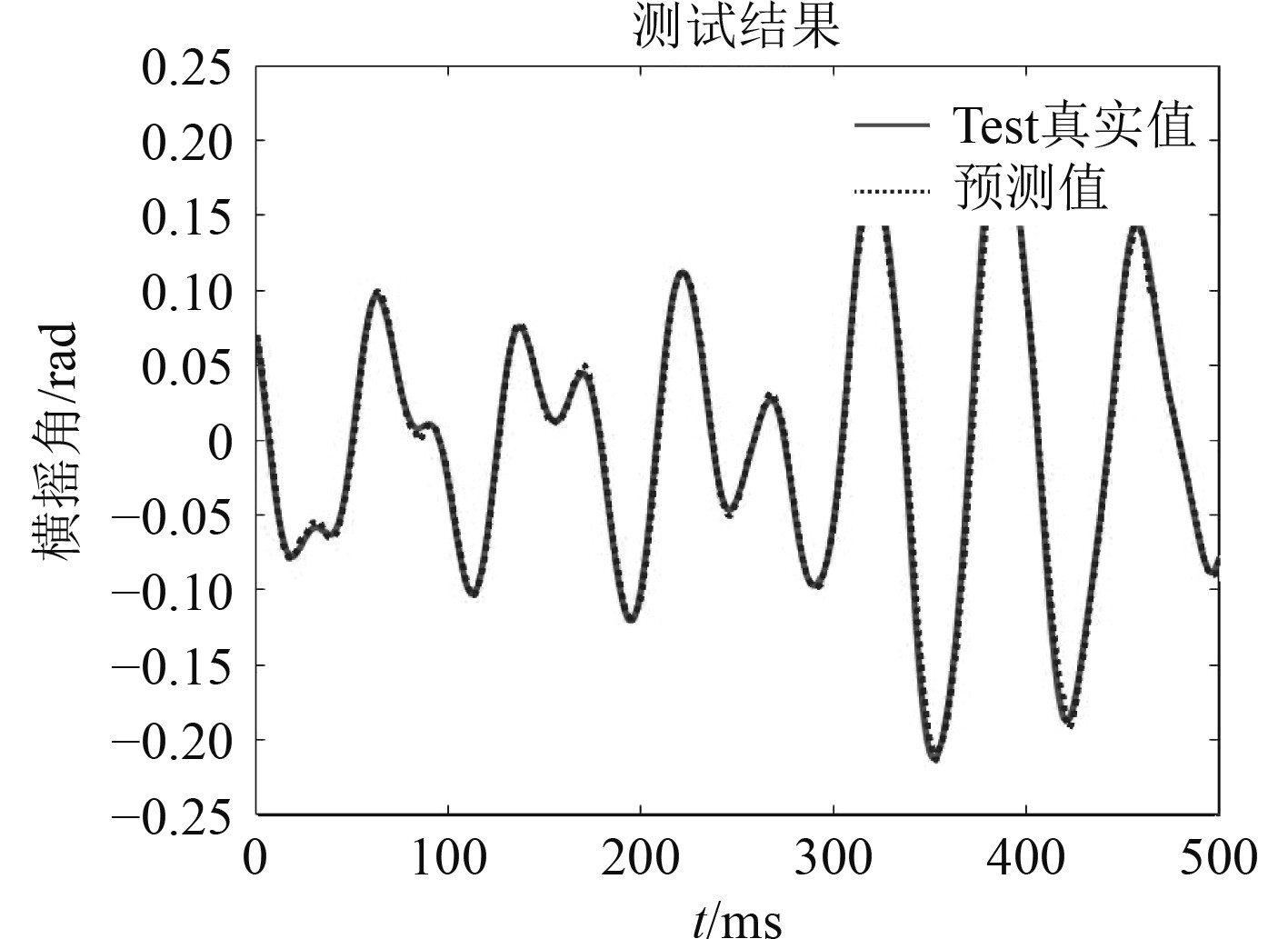
根据以上函数及加权参数的设定,BP神经网络和RF预测模型相融合后,对船舶横摇预测仿真结果如图6所示。
|
图 6 融合算法预测 Fig. 6 Fusion algorithm prediction |
基于BP神经网络预测和随机森林预测分别和融合预测的预测精度对比如表1所示。因BP神经网络本身受参数选择和初始权值的影响较大易过拟合或者欠拟合的缺点,而随机森林等算法在不同的具体问题上优势发挥不同,如设置不同的随机森林参数会有不同的效果,并且由于单一模型只能在预测的某一种趋势上效果较好,为能获得更好的预测效果,采用多种模型加权线性叠加的方法组合成更为精确的模型。由表1可看出,基于BP-RF算法的横摇预测模型具有较高的精度,相较于2种深度学习方法单独预测,其精度要提高0.02%~0.06%左右,具有较高的拟合度。
|
|
表 1 预测精度对比 Tab.1 Comparison of prediction accuracy |
在实际航行条件中为确保船舶上平台的稳定,需对船舶横摇进行预测,由于BP神经网络容易过拟合,且调参获得最优较为困难,使预测性能下降的缺点,本文将BP神经网络与随机森林相结合对船舶横摇进行预测,提高预测模型的准确性。根据Matlab仿真结果可以直观看出,相较与BP神经网络和随机森林单独进行预测,2种模型加权线性叠加的预测方法更为精确。
| [1] |
刘鹏, 籍艳, 漆随平, 等. 基于MATLAB的海浪及船舶横摇仿真模型研究[J]. 山东科学, 2012, 25(6): 87-89. |
| [2] |
张文桥. 动态海浪建模与仿真的关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [3] |
夏义. 船舶横摇运动仿真与减摇鳍控制系统的研究[D]. 大连: 大连海事大学, 2015.
|
| [4] |
NOVRI S, SUHARTONO, DEDY D P, et al. Roll motion prediction using a hybrid deep learning and ARIMA model[J]. Procedia Computer Science, 2018, 144. |
| [5] |
孙珊珊. 小波神经网络舰船运动受扰力预测模型[J]. 舰船科学技术, 2021, 43(8): 4-6. |
| [6] |
方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32-38. DOI:10.3969/j.issn.1007-3116.2011.03.006 |
| [7] |
王明瑞. 大型舰船运动交互预测中的多维度AR算法研究与仿真[J]. 舰船科学技术, 2021, 43(4): 10-12. |
| [8] |
李建平. 数据挖掘的高动态范围船舶横摇预测[J]. 舰船科学技术, 2018, 40(20): 20-22. |
 2022, Vol. 44
2022, Vol. 44
