2. 陆军装备部装备项目管理中心,北京 100072
2. Equipment Project Management Center of Army Equipment Department, Beijing 100072, China
随着无人机、无人艇、无人车等无人系统的蓬勃发展和市场化应用,未来将会有更多的人工作业被无人化方式取代,由各种类型的无人化设备去执行危险系数高、内容繁琐或批量化的作业任务。目前在海洋测量方面,已经实现了无人艇自动测量,但在近海、江河湖泊等浅水水域或密集通航的繁忙水域,无人化海洋测量存在着可航行吃水的制约。大型无人艇由于艇体宽大,可以承载体积更大的探测装置及大量附属设备,但其排水量大且吃水较深,在浅水区易搁浅,因而一般只用于深水区域的探测。为弥补该缺点,通常将测量无人艇小型化、模块化、规模化。
在海洋测量中,借助小型无人艇模块化的成本优势,使用编队协同与单艘无人艇相比具有明显的优势。首先,多艘无人艇可以分布在不同区域同时开展工作,对于不规则的测量区域,多艇协同作业,可以成倍提高测量效率;其次,编队内多个成员可分别携带不同的传感器,协同完成较为复杂的任务。此外,当编队中某个无人艇出现故障时,多无人艇系统可以通过任务重分配来自主调整测量方案,完成最终测量任务,从而提升了系统的任务适应性。
在无人艇编队控制方面,已经有了大量的学术研究成果,目前已经形成了3种常用的编队控制方法,分别为领航者-跟随者方法[1-2]、虚拟结构法[3-4]和行为法[5]。对于无人艇编队的海洋测量,采用前2种编队控制方法更适用。
无人艇编队执行海洋测量任务时,最简单的方式是所有无人艇组成单一编队,并按“一”字形排列。该方式可以单次测量较宽水域,具有很高的测量效率。但缺点是机动性能较差,难以适用于不规则水域的测量任务,且当编队内某成员出现故障时会影响到整个编队的行进。因此开展面向多任务的小型无人艇编队协同方案研究具有十分重要的研究意义和实用价值。
本文面向小型无人艇编队的海上测量任务,探讨研究了一种适用于多任务的高效协同控制方法。首先,针对多任务时的无人艇分配问题,设计了一种无人艇编队任务分配到的效能计算方法;对于常见的梳子形海洋测量路径的编队转弯问题,提出了一种自适应的编队队形重构方法;针对无人艇编队的引导问题,基于视线导航法设计了一种编队成员的航向与航速规划律。通过仿真试验,对提出方法的有效性进行了验证。
1 无人艇运动学模型在进行编队控制方法设计前,首先建立无人艇的运动学模型。定义一个由n艘船组成的欠驱动无人艇编队,并假设各船i以其中纵剖面对称,升沉、纵摇、横摇均忽略不计;随体坐标系的原点设在船舶中线上。根据文献[6-7]可知,对于
| $ {\dot {\boldsymbol{\eta}} _i} = \left[ {\begin{array}{*{20}{c}} {{{\dot x}_i}} \\ {{{\dot y}_i}} \\ {{{\dot \psi }_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _i}}&{ - \sin {\psi _i}}&0 \\ {\sin {\psi _i}}&{\cos {\psi _i}}&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_i}} \\ {{v_i}} \\ {{r_i}} \end{array}} \right],$ | (1) |
| $ \left\{ \begin{gathered} {\text{ }}{{\dot u}_i} = \frac{{{m_{22}}}}{{{m_{11}}}}{v_i}{r_i} - \frac{{{d_{11}}}}{{{m_{11}}}}{u_i} + \frac{1}{{{m_{11}}}}{\tau _{ui}},\hfill \\ {\text{ }}{{\dot v}_i} = - \frac{{{m_{11}}}}{{{m_{22}}}}{u_i}{r_i} - \frac{{{d_{22}}}}{{{m_{22}}}}{v_i} ,\hfill \\ {\text{ }}{{\dot r}_i} = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}{u_i}{v_i} - \frac{{{d_{33}}}}{{{m_{33}}}}{r_i} + \frac{1}{{{m_{33}}}}{\tau _{ri}} \hfill 。\\ \end{gathered} \right. $ | (2) |
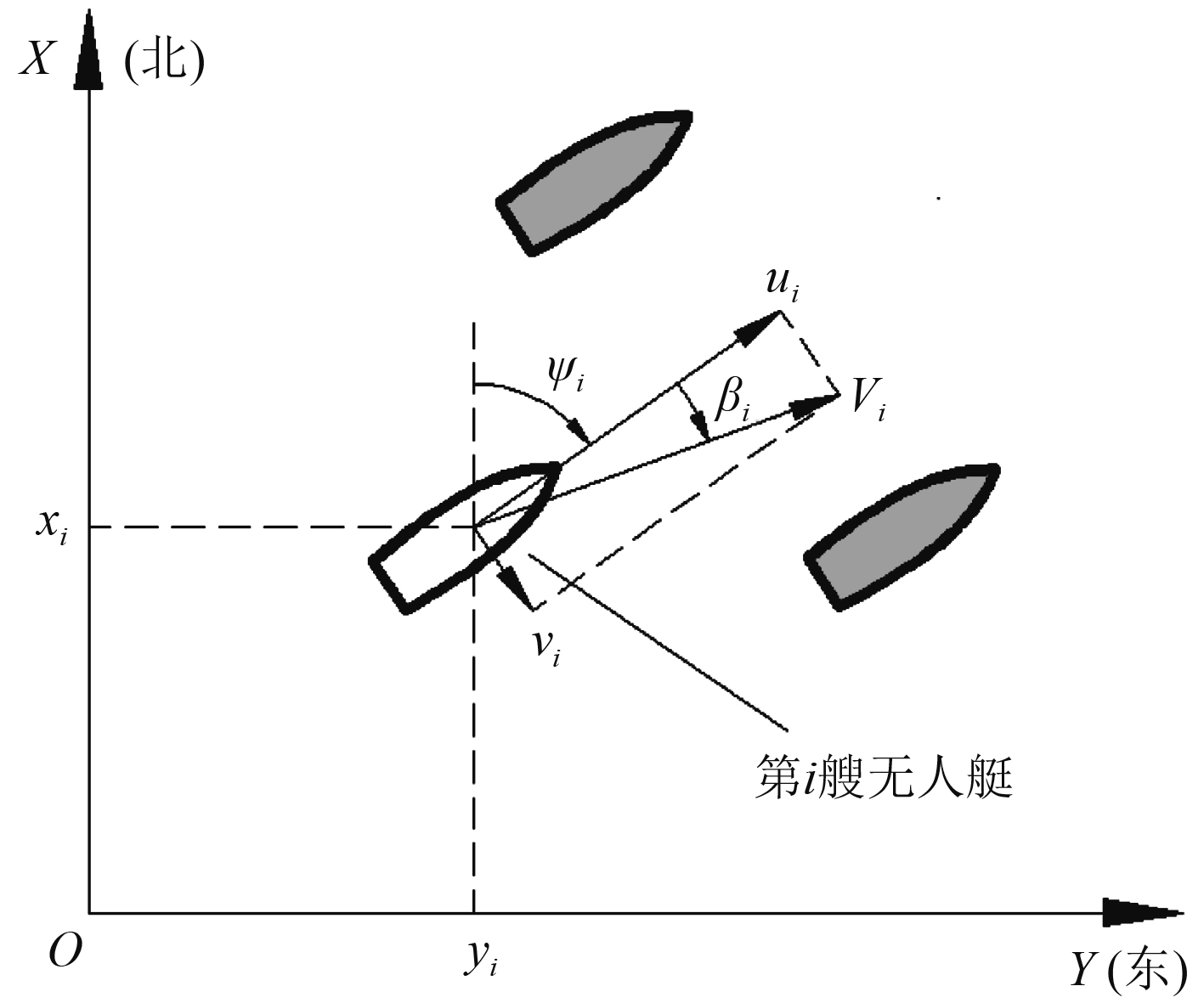
式中:(xi, yi)为第i艘船在大地坐标系下的中心位置(见图1);ψi为船的首向角;ui,vi,ri分别为船的前进速度,横漂速度和首摇角速度;前进推力τui和首摇力矩τri为系统控制输入量;m11和d11等参数分别由船舶惯性矩阵和阻尼矩阵给出,并假设其为正常数。
图1中:
|
图 1 无人艇运动坐标系示意图 Fig. 1 Schematic diagram of motion coordinate system of unmanned boat |
大规模小型无人艇集群在执行任务过程中,必然会存在资源调度和分配的问题。例如,使用无人艇集群进行区域海上测量,当无人艇集群的数量较多时,可以拆分为多个小编队执行一个或多个子任务。每个子任务可能位置及所需无人艇数量不同,若任务分配和资源调度过程全由人工完成,必然在时效性和资源消耗方面非最优状态。因此,有必要首先针对编队的指挥调度及任务分配进行理论方法研究。
无人艇的任务分配与编队重组问题,在数学层面上可以抽象为一个无人艇与对应任务之间的最优分配问题。针对该问题,可以借鉴匈牙利算法[8-9]进行功能实现。该算法最早由匈牙利数学家D.Konig提出,并被W.W.Kuhn进行改进,用来解决目标指派问题。
对于无人艇的任务分配,假设具有N个可用资源,以及M个子任务,求解总耗费最低的分配方式。定义任务关联矩阵RN×M,以及任务耗费矩阵CN×M如下:
| $ \begin{gathered} {\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{ \cdot \cdot \cdot }&{{r_{1M}}} \\ {{r_{21}}}&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot } \\ { \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot } \\ {{r_{N1}}}&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{{r_{NM}}} \end{array}} \right] ,\hfill \\ {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{ \cdot \cdot \cdot }&{{c_{1M}}} \\ {{c_{21}}}&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot } \\ { \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot } \\ {{c_{N1}}}&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{{c_{NM}}} \end{array}} \right] 。\hfill \\ \end{gathered} $ | (3) |
rij=1或0表示资源i是或否分配到任务j的关联判断,cij表示资源i关联到任务j的耗费。此外,由于每个资源i只能关联到1个任务,因此关联矩阵满足条件各行及各列元素之和为1,即
| $ \begin{gathered} \sum\limits_{i = 1}^N {{r_{ij}}} = 1{\text{ }}(j = 1,2,...,M),\hfill \\ \sum\limits_{j = 1}^M {{r_{ij}}} = 1{\text{ }}(i = 1,2,...,N) ,\hfill \\ \end{gathered} $ | (4) |
则最优分配问题可以进一步定义为求解分配总耗费Z的最小值,分配问题的数学模型可定义为:
| $ {\text{min Z}} = \min ({C^{\rm{T}}}R) = \min \left(\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{c_{ij}}{r_{ij}}} } \right) 。$ | (5) |
“匈牙利法”的计算基础和前提是:从耗费矩阵的每一行(或每一列)元素中分别减去(或加上)一个常数,使得每一行(每一列)里至少有一个0元素;得到新的耗费矩阵,并用该矩阵代替原矩阵,且不改变分配问题的最优解。上述模型的数学意义是,效能矩阵中的每一行、每一列均能得到0。
分析模型(5)可知,要实现无人艇任务的高效、合理分配,关键点在于耗费矩阵C的影响因素及权重是否设计合理。根据无人艇任务自主分配与编队重组的场景,各无人艇即为一个将任务耗费cij设计为资源-任务距离dij,以及无人艇i首向与任务j相对角度差值φij的相关函数。
| $ \left\{ \begin{gathered} {c_{ij}} = {k_1}\sqrt {\left| {{\varphi _{ij}}} \right|} + {d_{ij}}^2 ,\hfill \\ {\varphi _{ij}} = \max \{ [{\psi _i} - {a{\rm{tan}}} 2({y_j} - {y_i},{x_j} - {x_i})],{5^ \circ }\} ,\hfill \\ {d_{ij}} = \sqrt {[{{({x_i} - {x_j})}^2} + {{({y_i} - {y_j})}^2}]} 。\hfill \\ \end{gathered} \right. $ | (6) |
式中:(xi, yi)及(xj, yj)分别表示无人艇i及任务j的坐标位置;k1为相对角度φij的权重调节参数。当φij值小于5°时,将视为只考虑相对距离的影响。
设计得到耗费矩阵的具体计算表达式后,关于匈牙利算法最优分配的具体计算步骤,在文献[10]中已有较为详尽的介绍。
2.2 面向任务路径的编队队形自适应重构方法在海洋测量任务中,无人艇编队成员没有明显的主从关系,因而可采用虚拟结构的编队控制方法。在该方法中,存在一个虚拟领航点,编队内各成员与该点保持固定的位置关系,从而编队呈现期望的队形。
无人艇编队的期望路径可由一系列离散路径点的连线构成,定义期望路径PK在大地坐标系下的位置为(xpK, ypK),K=1, 2
定义虚拟领航点的坐标为(xl, yl),初始时刻虚拟领航者随体坐标系下无人艇i的队形为li=(lxi, lyi)T,编队期望航速为ul。则任意时刻下,虚拟领航者的位置为:
| $ \left[ \begin{gathered} {x_l} \hfill \\ {y_l} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} x{p_K} \hfill \\ y{p_K} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _K}}&{ - \sin {\alpha _K}} \\ {\sin {\alpha _K}}&{\cos {\alpha _K}} \end{array}} \right]\left[ \begin{gathered} {u_l}{t_K} \hfill \\ 0 \hfill \\ \end{gathered} \right] 。$ | (7) |
式中:tK表示领航者在第K段路径上运动的时间。
进一步可以计算得到第i艘无人艇的期望位置(xid, yid),然而在队形设计时,常规的设计方式为编队队形固定,计算方法如下[11]:
| $ \left[ \begin{gathered} {x_{id}} \hfill \\ {y_{id}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {x_l} \hfill \\ {y_l} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _K}}&{ - \sin {\alpha _K}} \\ {\sin {\alpha _K}}&{\cos {\alpha _K}} \end{array}} \right]\left[ \begin{gathered} l{x_i} \hfill \\ l{y_i} \hfill \\ \end{gathered} \right]。$ | (8) |
当路径切换,无人艇编队需要转弯时,整个队形随着虚拟领航者的首向改变而改变,通常会根据队形大小规划出相对曲率较大的路径,以确保整个编队在弯道可以平滑的过度。
然而对于应用在海洋测量场景中的小型无人艇编队,由于测线多是平行布置的往返路径,虚拟领航者在转弯时首向变化时往往伴随着较大的角速度变化,甚至出现虚拟领航者首向跳变,致使整个队形混乱。此外,该方式转弯过程中,编队外侧无人艇需要更大的航速来保持队形一致,且过大的整体回转半径会降低整体测绘效率。因而式(8)中的编队队形方式不适合编队海洋测量的应用场景。
为解决上述编队队形控制方案存在的不足,提出了一种自适应测量路径的编队队形重构方法,达到队形随路径调整的效果。将第i艘无人艇的期望位置按如下方法重新定义:
| $ \left[ \begin{gathered} {x_{id}} \hfill \\ {y_{id}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {x_l} \hfill \\ {y_l} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _1}}&{ - \sin {\alpha _1}} \\ {\sin {\alpha _1}}&{\cos {\alpha _1}} \end{array}} \right]\left[ \begin{gathered} l{x_i} \hfill \\ l{y_i} \hfill \\ \end{gathered} \right] 。$ | (9) |
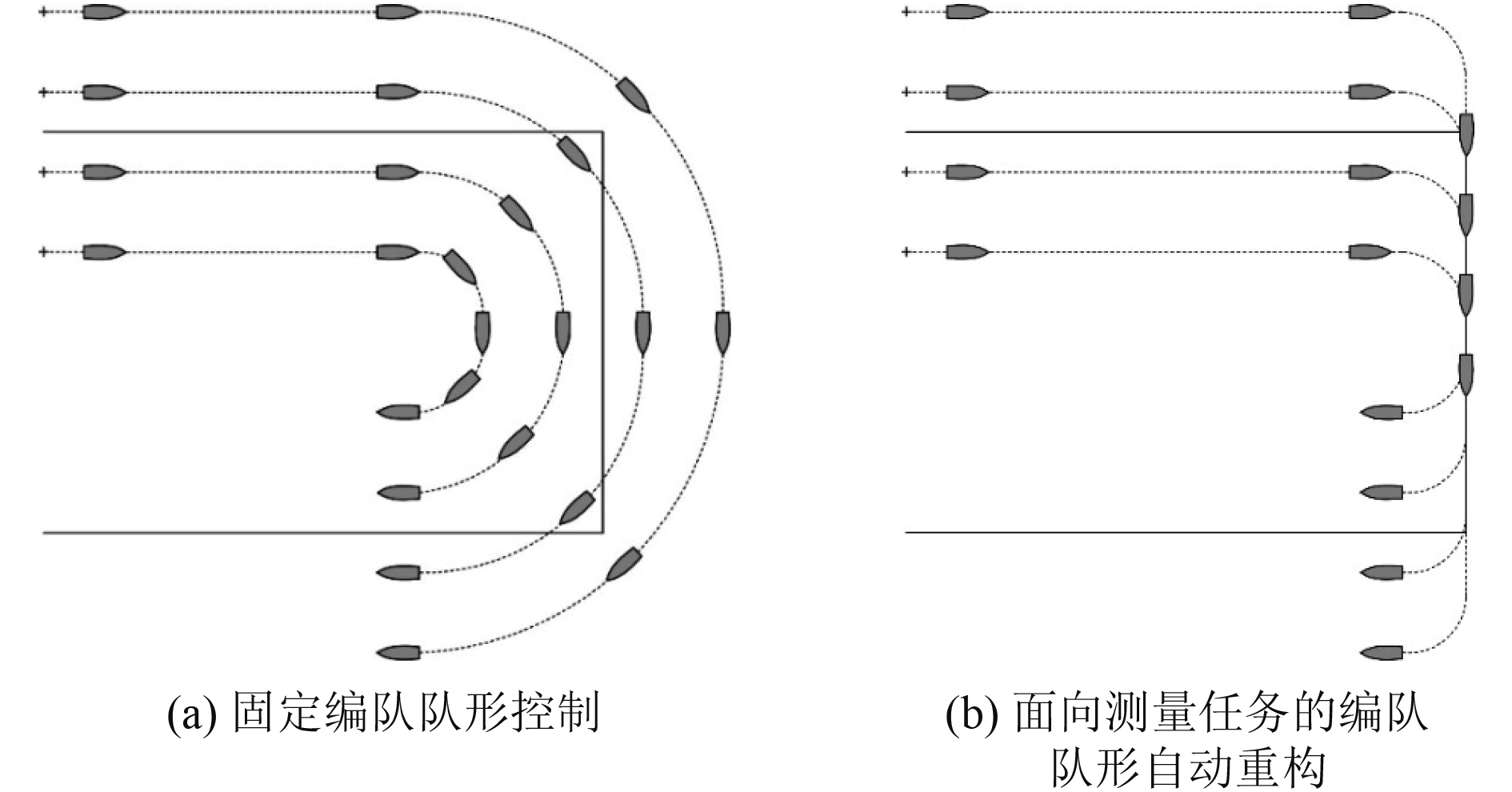
式(8)与式(9)两种编队队形控制方法的航行示意图如图2所示。
|
图 2 两种编队队形控制方案的航行效果示意图 Fig. 2 Schematic diagram of navigation effect of two formation control schemes |
图2(a)为编队队形固定的方式,假设最内侧无人艇航速为6 kn,若想要保持队形稳定,最外侧无人艇航速需要达到24 kn,若编队中无人艇数量较多,则最外侧无人艇航速需要更大,而用于海洋测量的小型无人艇最高航速远达不到该速度,况且海洋测量仪器对无人艇最高航速也有限制,一般6 kn较为理想。该方式也会导致无人艇编队测量较多的无关水域,较低测量效率;
如图2(b)所示的自适应测量路径的编队队形重构方式,可以在无人艇编队整体航速保持不变,并且不影响测量效果的情况下,编队队形从各艇之间相对平行的方式重构为各艇排成一列的方式,等到达下一转弯处时,重新回构成相对平行的方式继续测量任务。
自适应测量路径的编队队形重构这种方式更适用于海洋测量的环境,测量效率更高,稳定的速度对测量数据具有保障性。
2.3 无人艇编队运动规划律完成无人艇编队队形设计后,要实现无人艇编队的协同航行,还需要进一步完成各无人艇航速及航向控制律的设计。需要说明的是,对无人艇而言,航速与航向控制的耦合度很低,通常对航速及航向进行分离控制。
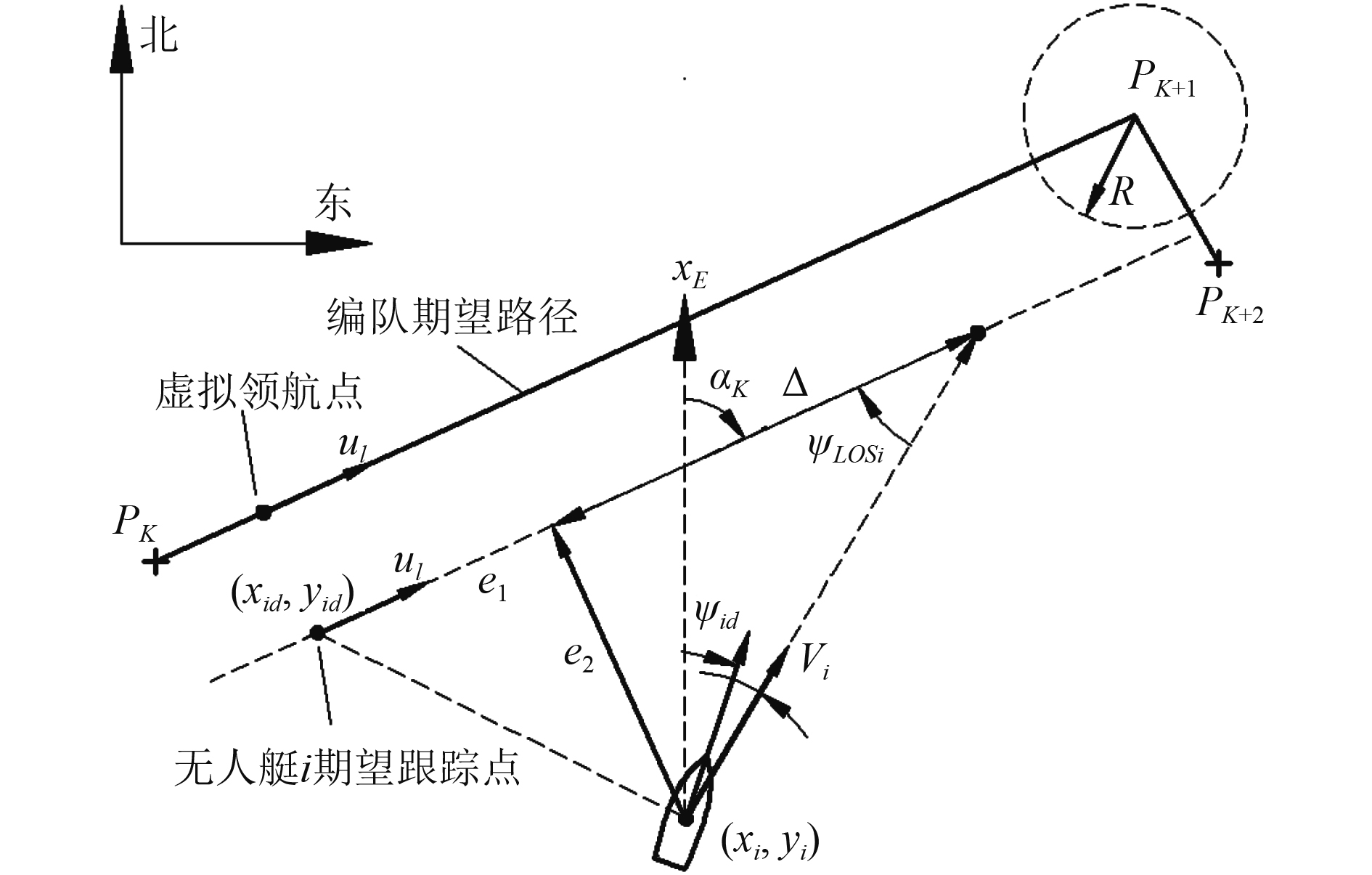
针对编队控制的无人艇首向规划律如图3所示。
|
图 3 无人艇首向规划律示意图 Fig. 3 Schematic diagram of heading planning law of unmanned boat |
式(9)中的规划律,可以理解为各无人艇i均在执行对各自期望路径
| $ \left[ {\begin{array}{*{20}{c}} {{e_{i1}}} \\ {{e_{i2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _K}}&{\sin {\alpha _K}} \\ { - \sin {\alpha _K}}&{\cos {\alpha _K}} \end{array}} \right]\left[ \begin{gathered} {x_i} - {x_{id}} \hfill \\ {y_i} - {y_{id}} \hfill \\ \end{gathered} \right] ,$ | (10) |
要实现无人艇编队队形的维持,只需各无人艇的纵向及横向误差均趋于0即可,即控制目标为实现(ei1, ei2)→(0, 0)。
对式(10)两边求导可得,
| $ \left\{ \begin{gathered} {{\dot e}_{i1}} = {u_i}\cos ({\psi _i} - {\alpha _K}) - {v_i}\sin ({\psi _i} - {\alpha _K}) - {u_l} ,\hfill \\ {{\dot e}_{i2}} = {u_i}\sin ({\psi _i} - {\alpha _K}) + {v_i}\cos ({\psi _i} - {\alpha _K}) ,\hfill \\ \end{gathered} \right. $ | (11) |
针对横向误差的镇定控制,可使用视线引导律(Line-of-sight)。该引导方法广泛应用于无人艇、水下机器人等对象的直线路径跟踪控制中[12]。设计各无人艇的期望舵角ψid如下:
| $ \left\{ \begin{gathered} {\psi _{id}} = {\alpha _K} + {\psi _{LOSi}} - {\beta _i} ,\hfill \\ {\psi _{LOSi}}{\text{ = }}\arctan \left( { - \frac{{{e_i}}}{\Delta }} \right)。\hfill \\ \end{gathered} \right. $ | (12) |
式中:Δ>0表示视线法中的前视距离,无人艇始终朝向到期望航线投影点前方距离Δ的点航行,ψLOSi表示无人艇到该点连线与期望航线的夹角。
定义Lyapunov函数
| $\begin{split} {\dot V_1} =& {e_{i2}}\left[ {{u_i}\sin ({\psi _i} - {\alpha _K}) + {v_i}\cos ({\psi _i} - {\alpha _K})} \right] = \\ &{e_{i2}}{V_i}\sin ({\psi _i} - {\alpha _K} + {\beta _i})。\end{split}$ | (13) |
无人艇的航速及航向控制律已经有了大量的研究,研究成果涵盖PID、滑模控制法、模糊控制律、自适应控制方法、神经网络等大量的控制方法。因此本文不再对航速、航向控制律进行说明,重点针对编队内各成员的首向引导律进行设计,从而提出以下前提假设:
假设1在适当的航速与航向分离控制律作用下,无人艇的实时航速与航向即为期望航速及期望航向,即满足ui=uid,ψi=ψid。
将假设1代入式(13)可得:
| $ \begin{split} {\dot V_1} =& {e_{i2}}{V_i}\sin ({\psi _{LOSi}}) =\\ &{e_{i2}}{V_i}\frac{{\sin ({\psi _{LOSi}})}}{{{\psi _{LOSi}}}}\arctan ( - {e_{i2}}/\Delta ) \leqslant \\ &-\frac{{{V_i}\sin ({\psi _{LOSi}})}}{{\Delta {\psi _{LOSi}}}}{e_{i2}}^2 \leqslant 0 。\end{split}$ | (14) |
从而上式满足渐进收敛的条件,横向误差ei2在首向引导律的作用下将逐渐收敛于0,即无人艇将逐渐达到对应的期望航线,并沿期望航线航行。
在航速规划律方面,设计期望航速为之与期望点运动速度和无人艇纵向误差相关的函数如下:
| $ {u_{id}} = {u_l} - {k_2}{e_{i1}} 。$ | (15) |
式中:k2为正的控制参数。
设计Lyapunov函数
| $ \begin{split} {\dot V_2} = & {e_{i1}}({u_i}\cos {\psi _{LOSi}} - {v_i}\sin {\psi _{LOSi}} - {u_l}) =\\ & {e_{i1}}({u_{id}} + {u_{id}}(\cos {\psi _{LOSi}} - 1) -\\ &{v_i}\sin {\psi _{LOSi}} - {u_l}) \leqslant - {k_2}{e_{i1}}^2 + \rho 。\end{split}$ | (16) |
其中:
由于航速和航向控制是分离的,在横向误差逐渐收敛的情况下,ρ也将趋近于0。因此纵向位置误差也是渐进收敛的。从而在有限时间内,ei1与ei2都将收敛于0。
3 仿真试验为了对所设计的编队运动规划及任务分配方法进行验证,以SE40小型测量无人艇作为仿真对象,进行4艘编队航行的仿真试验。该艇主体长、宽、高分别为1.5 m×0.7 m×0.4 m,吃水0.2 m,空载重量32 kg,负载能力25 kg。在2 m/s和6 m/s的工作航速下,续航时间分别为4 h和2 h。在无人艇的底层运动控制方面,使用了文献[13]中的自抗扰鲁棒控制律,分别对无人艇的航速与航向进行独立控制。
在仿真中,选取任务分配相关的权重调节参数k1=10,首向规划律的前视导引距离Δ=10 m,航速规划律参数k2= 0.1。
3.1 任务分配仿真仿真中,编号1~4号无人艇初始位置如图4所示。在t =0时刻,编队控制中心同时下发2条测量任务,分别为:外侧的测量路线1,编队成员需求为1,期望航速为4 kn,编队期望队形向量为(lx1, ly1)=(0, 0);内侧的测量路线2,成员数量为3,期望队形向量为(lx1, ly1)=(0, −30 m),(lx2, ly2)=(0, 0),(lx3, ly3)=(0, 30 m)。

|
图 4 无人艇接收到任务指令并开始执行任务 Fig. 4 Unmanned boat receives mission and execute |
编队上层控制节点根据任务路线、任务中的队形需求、以及各无人艇的当前位置,自动计算并分配距离外侧路线起始点最近的1号无人艇执行任务1;2~4号无人艇被分配执行任务2,并根据相对位置自动分配2~4号无人艇从左至右排列。
图5展示了4艘无人艇依次到达指定位置点,在编队运动引导律及底层控制律的联合控制下,保持指定队形,并沿期望航线执行协同测量的任务。

|
图 5 无人艇编队分小组进行协同测量任务 Fig. 5 Unmanned formation team execute coop measure mission |
完成测量任务后,各无人艇分别在原地执行小半径回转任务等待新任务。若编队控制中心下发任务结束指定,则各无人艇返回至指定集结点;若指挥中心重新下发新任务,则无人艇根据新任务信息,重组编队继续开展测量任务。
图6展示了1~4号无人艇完成测量任务后,各自在原地回转待命,一段时间后,编队控制中心下发观测任务3。任务3的编队期望航速不变,编队成员数量为4,期望队形向量为(lx1, ly1)=(0, −45 m),(lx2, ly2)=(0, −15 m),(lx3, ly3)=(0, 15 m),(lx4, ly4)=(0, 45 m)。接收到新任务指令后,编队控制中心自动对4艘无人艇进行编队重组,并根据总耗费值最小的原则分配1~4号无人艇依次从左至右排列,分别对应新编队中的4号、3号、2号、1号成员。无人艇在期望跟踪点的引导下,完成整体队形的调整。

|
图 6 无人艇进行编队重组 Fig. 6 Formation reorganization of unmanned craft |
图7展示了新组成的编队保持期望队形,沿新的期望航线执行测量任务。当编队从第3段路径切换到跟踪第4段路径时,编队成员自动从横向成员排列转换为纵向成员排列,实现编队队形重构及跟踪路径调整。

|
图 7 无人艇编队队形重构 Fig. 7 Formation reconstruction of unmanned craft |
本文针对小型无人艇编队协同控制问题,分别从任务自主分配、编队队形自适应重构、无人艇运动规划律3个方面开展方法设计。针对任务自主分配,在匈牙利算法基础上,设计了一种距离-相对角度的复合型耗费评价方法;为适应编队海上测量的控制需求,提出了一种航行变换时编队队形自动重构的简易实现方法;针对所设计的编队队形控制方案,基于视线引导法,提出了一种航速、航向分离控制的运动规划律。最后,进行了4艘同型无人艇的编队航行仿真试验,对多任务自动分配、编队队形自动重构、编队运动规划律等层面设计方法的可行性和有效性进行了验证。
| [1] |
PENG Z, WANG D, CHEN Z, et al. Adaptive dynamic surface control for formations of autonomous surface vehicles with uncertain dynamics[J]. Control Systems Technology, IEEE Transactions on. 2013, 21(2): 513-520.
|
| [2] |
CHEN, Y, TIAN, Y. Formation tracking and attitude synchronization control of underactuated ships along closed orbits[J]. International Journal of Robust & Nonlinear Control, 2015, 25(16): 3023-3044. |
| [3] |
DO K D. Practical formation control of multiple underactuated ships with limitedsensing ranges. Robotics and Autonomous Systems, 2011, 59: 457-471.
|
| [4] |
刘国芳, 冯王兵, 罗佳. 考虑运动模式的无人船航迹实时跟踪控制算法[J]. 舰船科学技术, 2021, 43(4): 16-18. |
| [5] |
KUPPAN C R M, SINGAPERUMAL M, NAGARAJAN T. Behavior based multi robot formations with active obstacle avoidance based on switching control strategy[J]. Advanced Materials Research, 2012, 433: 6630-6635. |
| [6] |
FOSSEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles[M]. Trondheim, Norway: Marine Cybernetics, 2002.
|
| [7] |
DO K D. Practical control of underactuated ships[J]. Ocean Engineering, 2010, 37(13): 1111-1119. DOI:10.1016/j.oceaneng.2010.04.007 |
| [8] |
马硕, 马亚平. 基于分层聚类拍卖的集群UUV多目标分配方法[J]. 舰船科学技术, 2019, 41(9): 70-75. |
| [9] |
吕光颢, 彭周华, 王丹, 等. 无人船集群队形重构的目标任务分配[J]. 中国舰船研究, 2018, 13(6): 103-108. |
| [10] |
吴祈宗, 侯福均. 运筹学与最优化方法[M]. 北京: 机械工业出版社, 2013.
|
| [11] |
丁磊, 郭戈. 一种船队编队控制的backstepping方法[J]. 控制与决策, 2012, 27(2): 299-303. |
| [12] |
Oh S R, Sun J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control[J]. Ocean Engineering, 2010, 37(2): 289-295. |
| [13] |
田晓伟. 舰船航向非线性自适应鲁棒控制方法[J]. 舰船科学技术, 2020, 42(14): 55-57. |
 2022, Vol. 44
2022, Vol. 44
