近年来,随着人工智能技术不断发展,无人船技术研究不断深入,其中路径规划技术作为保证安全航行的关键,成为了目前研究的热点方向。无人船路径规划根据路径中所遇障碍物运动状态的不同,可将路径规划问题划分为静态和动态2种。其中,应用更加广泛的路径规划技术是动态技术,其特点在于可以满足船舶航行过程中实时决策的需要,进而规划最优的导航路线,及时避开路线障碍物。由于在新环境的感知问题上存在很大差异,一般用两类问题来概括描述无人船的路径规划问题:第一类称之为全局路径规划;第二类称之为局部路径规划。第一类全局路径规划的开始时间早,需要在航行任务开始前,就对航行廊道空间范围内的障碍物进行分析预判,根据其分布合理规划航行路线[1];局部路径规划仅需要对航行路线中的障碍物进行局部感知,规划的航线范围也仅为包含障碍物在内的局部空间,分区域的多个局部空间内的最优航线最终形成最优的无障碍航行。此外,局部路径规划还具有实时规划的特点[2]。
研究人员对无人船的路径规划技术进行了大量的研究,创造出了如模糊控制法,遗传算法、神经网络算法及人工势场法等一系列的显著成果。但相比之下,人工势场法具有反应速度较快、实时性较为敏捷、计算量较少等特点,在实际的无人船路径规划问题中得到了广泛的应用。但是当目标点附近存在障碍物时,无人船将在目标点附近震荡,无法真正到达目标点;同时,受障碍物影响,无人船路径规划过程中容易陷入局部最优。
因此,本文针对人工势场算法应用与无人船航迹规划中存在的问题展开研究,通过对斥力场函数的优化以及逃逸力的增加,改进人工势场算法,从而解决目标不可达问题以及局部极小值问题,获得从起始点到目标点的一条最优无碰撞路径。仿真验证结果表明,改进后的人工势场算法可实现无人船在最优路径上安全、稳定地航行。
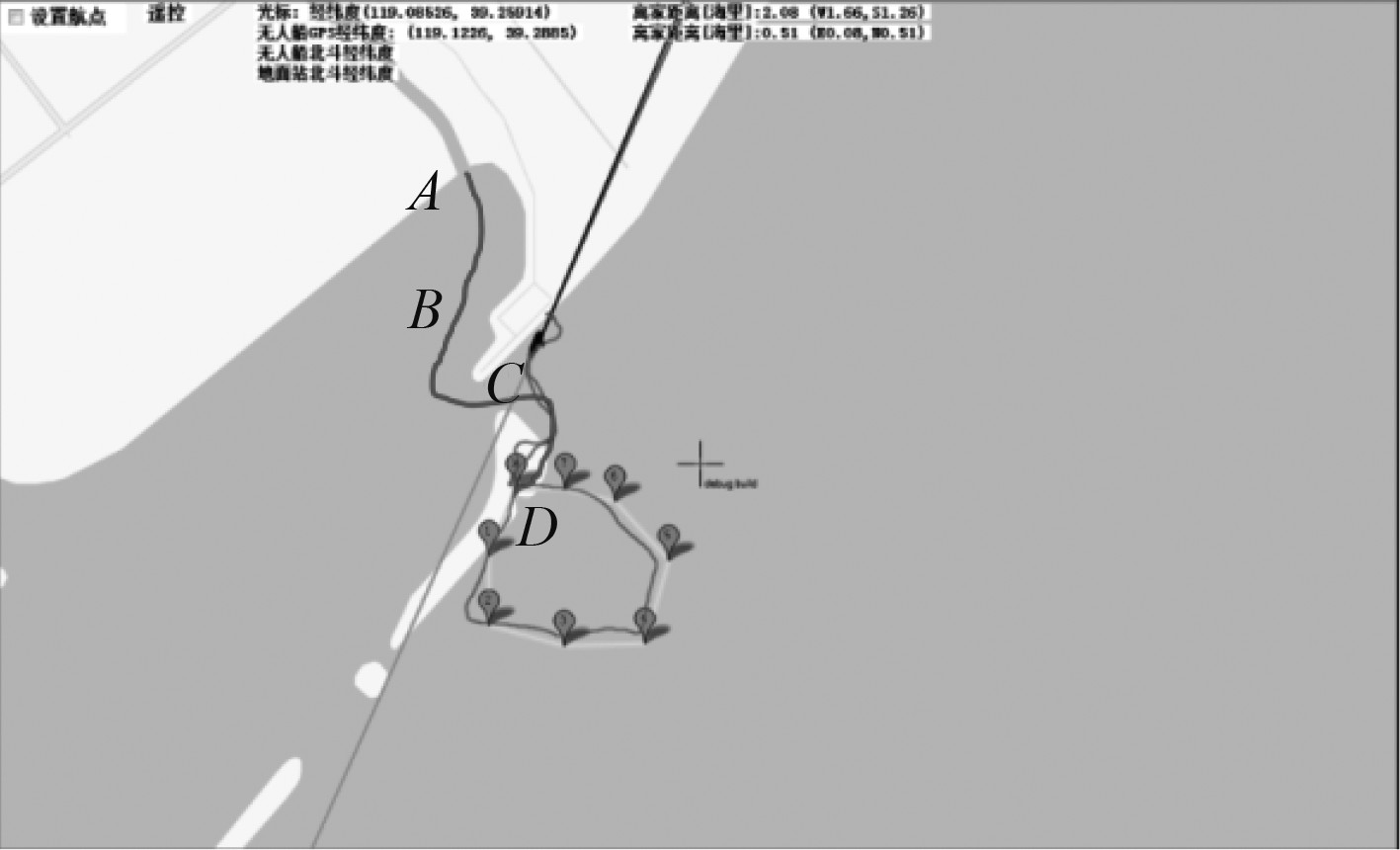
1 基于人工势场法路径规划算法水面无人艇任务规划主要针对不同任务类型进行规划,例如某无人船驶离避风港到达海域的过程。图1为某海域无人船驶经港口的示意图,图中A点为无人船的出发点,也即为路径规划的起始点,B,C,D为规划路径中经过的点,D点为最终的目标点。A,B,C,D点构成的路线即为无人船驶离避风港到达海域的规划航行路径。
|
图 1 无人船驶经港口示意图 Fig. 1 Schematic diagram of the unmanned ship sailing through the port |
采用人工势场法对无人船驶离避风港到达海域的问题进行分析。无人船在A点受到引力势场的作用,引力势场大小由A点(起始点)到D点(目标点)的距离决定,表达式如下:
| $ {U_{\text{a}}}{\text{ = }}\frac{1}{2}\eta [{(\chi - {\chi _g})^2} + {(y - {y_g})^2}] 。$ | (1) |
其中:
吸引力函数可定义为下式:
| $ {F_a} = - \nabla ({U_a}) = \left[ { - \eta (x - {x_g}), - \eta (y - {y_g})} \right],$ | (2) |
吸引力的大小为:
| $ \left| {{F_a}} \right| = \eta \sqrt {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}}。$ | (3) |
因此可知,无人船与目标点的吸引力随着间距变大而变大。当无人船到达目标点时,其受到的吸引力变为0。
无人船在A点(起始点)还受到排斥力势场的作用,记为
| $ {U_r} = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}\xi \left(\dfrac{1}{\rho } - \dfrac{1}{{{\rho _d}}}\right),&\rho < {\rho _d} ,\\ 0,&\rho \geqslant {\rho _d} 。\end{array}} \right. $ | (4) |
其中,用
| $ {F_r} = - \nabla ({U_r}) = \frac{\xi }{{{\rho ^2}}}\left(\frac{1}{\rho } - \frac{1}{{{\rho _d}}}\right)\left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {U_r}}}{{\partial x}}}&{\dfrac{{\partial {U_r}}}{{\partial y}}} \end{array}} \right] ,$ | (5) |
则最终的排斥力表达式如下:
| $ \left|{F}_{r}\right|=\left\{\begin{array}{*{20}{l}}\dfrac{\xi }{{\rho }^{2}}\left(\dfrac{1}{\rho }-\dfrac{1}{{\rho }_{d}}\right),&\rho < {\rho }_{d},\\ 0\text{,}&\rho \geqslant {\rho }_{d}。\end{array}\right. $ | (6) |
由上式可以看出:当无人船的航进方向上存在有障碍物且其向障碍物方向靠近时,越逼近障碍物,障碍物作用在无人船的排斥力越大。为更为准确地将其受到的排斥力进行定量表示,在坐标轴中将其受到的排斥力进行分解。作用于无人船的排斥力与坐标轴之间的夹角为:
| $ \phi {\text{ = }}\arccos \left(\frac{{x - {x_d}}}{{\sqrt {{{(x - {x_d})}^2} + {{(y - {y_d})}^2}} }}\right),$ | (7) |
则排斥力在2个坐标轴上的分量如下式:
| $ \begin{array}{l}\left|{F}_{rx}\right|=\left\{\begin{array}{*{20}{l}}\left|{F}_{r}\right|·\mathrm{cos}\varphi ,&\rho < {\rho }_{d},\\ 0,&\rho \geqslant {\rho }_{d},\end{array}\right.\\ \left|{F}_{ry}\right|=\left\{\begin{array}{*{20}{l}}\left|{F}_{r}\right|·\mathrm{sin}\varphi ,&\rho < {\rho }_{d},\\ 0,&\rho \geqslant {\rho }_{d}。\end{array}\right.\end{array} $ | (8) |
因此,无人船在航进过程中,作用于其的总势场为
由以上分析可知,无人船在D点(目标点)的引力势场和途中障碍物斥力势场的联合作用下,会自动识别规划路径中的障碍物,并进行躲避,不断接近D点(目标点),最终实现整个航行。
2 改进的人工势场路径规划技术 2.1 斥力场函数优化在解决无人船的路径规划问题过程中,当采用传统的人工势场法时,若障碍物存在于目标点附近,无人船便无法真正到达目标点。究其原因,主要是由于此时无人船受到的目标点引力几乎为0,但是来自障碍物的斥力不为0,无人船会在目标点附近连续震荡,无法真正达到目标点[3]。
上述问题可概括为“目标不可达”问题,为解决此问题,学者Krogh开展了大量的分析与计算,根据计算结果修改了人工势场法的传统函数,修改后函数如下:
| $ {U_r} = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}\xi {{(\dfrac{1}{\rho } - \dfrac{1}{{{\rho _o}}})}^2}\left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right],&\rho < {\rho _o} ,\\ 0,&\rho \geqslant {\rho _o} 。\end{array}} \right. $ | (9) |
由上式可以得出,当无人船与目标点的距离无限逼近时,其受到的斥力场无限逼近于0,进而保证无人船在目标点时作用在其上的合力接近于0,其中受到的排斥力可表示如下:
| $ \begin{split} {F_{rx}} = & - {\nabla _x}({U_r}) = - \xi (x - {x_g}){\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)^2} +\\ &\xi \left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)\frac{{x - {x_o}}}{{{\rho ^3}}} ,\\ {F_{ry}} = & - {\nabla _y}({U_r}) = - \xi (y - {y_g}){\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)^2} +\\ &\xi \left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)\frac{{y - {y_o}}}{{{\rho ^3}}} ,\\ \left| {\overrightarrow {{F_r}} } \right| = &\sqrt {{F^2}_{rx} + {F^2}_{ry}} 。\end{split} $ | (10) |
可以看出,新的排斥力函数计算结果表明,无人船在无限接近障碍物时受到的作用力衰减为0。但是也引发一个新的问题,当无人船处于目标点周围以外的位置时,作用于其的合理明显大于传统的算法,这会导致无人船在增大的排斥力的作用下会偏离基于传统人工势场法规划航行的路径,而且由于斥力增大的原因,无人船到达目标点所需要经历的总的航进里程会被增大,相对应的,其计算得出的航进路线方案也不再是最优方案[4]。
针对上述路径增长问题,一种新的斥力场函数随之被提出并加以应用,其可同时有效解决“目标不可达”问题和“规划路径变长”的问题,该斥力函数表达式如下:
| $ {U_r} = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}\xi {{\left(\dfrac{1}{\rho } - \dfrac{1}{{{\rho _o}}}\right)}^2}\left[ {1 - \exp \left( - \dfrac{{\left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]}}{{{R^2}}}\right)} \right],\\ \rho < {\rho _o} ,\\ 0,\rho \geqslant {\rho _o}。\\ \end{array}} \right. $ | (11) |
从而对其排斥力可描述如下:
| $ \begin{split} {F_{rx}} =& - {\nabla _x}({U_r}) = - \xi (x - {x_g}){\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)^2}\times\\ &\exp \left( - \frac{{\left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]}}{{{R^2}}}\right)+\\ &\xi \left[ {1 - \exp \left( - \frac{{\left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]}}{{{R^2}}}\right)} \right]\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)\frac{{x - {x_o}}}{{{\rho ^3}}} ,\\ {F_{ry}} =& - {\nabla _y}({U_r}) = - \xi (y - {y_g}){\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)^2}\times\\ &\exp \left( - \frac{{\left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]}}{{{R^2}}}\right) +\\ &\xi \left[ {1 - \exp \left( - \frac{{\left[ {{{(x - {x_g})}^2} + {{(y - {y_g})}^2}} \right]}}{{{R^2}}}\right)} \right]\left(\frac{1}{\rho } - \frac{1}{{{\rho _o}}}\right)\frac{{y - {y_o}}}{{{\rho ^3}}},\\ \left| {\overrightarrow {{F_r}} } \right| =& \sqrt {{F^2}_{rx} + {F^2}_{ry}} 。\\[-15pt] \end{split} $ | (12) |
由上式得出:当无人船接近目标点,即
根据上文所提基于改进人工势场算法的路径规划技术可以发现,无人船按照规划路径进行航行时,可能会出现受到目标点的吸引力与受到障碍物的排斥力相互抵消的情况,此时,无人船出现误认为到达目标点的情况,正常航进终止,局部极小值问题出现,目标点无法抵达。
为了避免上述问题的出现保证无人船顺利到达目标点,需结合多种函数将传统的人工势场法进行优化设计。
正常航行中的无人船出现受到目标点的吸引力与受到的障碍物的排斥力相抵消的情况,大概可分为以下几种可能:1)当无人船行进方向为障碍物与目标点所在的直线时,若障碍物距离目标点较近,且目标点相较于障碍物距离无人船更近,无人船可能会出现因吸引力与排斥力相等而抵消的问题,进而使其陷入局部极小值问题而停止航进;2)当无人船行进方向为障碍物与目标点所在的直线时,若障碍物距离目标点较近,且障碍物相较于目标点距离无人船更近,无人船同样会陷入局部极小值问题而停止航进[5]。3)当多个障碍物同时存在并出现在无人船的航进方向上时,可能会导致其同时受到的多个斥力的合力与吸引力平衡抵消,即
为避免无人船在航行中陷入局部极小值,有必要判断其是否停止正常航进,进而判定其是否处于局部最小值状态。总结现有研究成果发现,判定无人船是否陷入局部极小值,需要检验其是否同时达到以下2个条件:1)未到达目标点;2)接连进行了多次移动但移动距离均低于正常航进步长[1]。
专家学者对于无人船在航行中陷入局部最小值的问题进行了研究并提供了一些解决方法,主要包含但不限于以下4种:1)随机逃走法;2)模拟退火算法;3)遗传算法;4)角度偏移法。本文对无人船在航行中是否陷入局部最小值进行判断,如果判断无人船在航行中陷入了局部极小值,则采用引入逃逸力的方法来解决上述问题。
本文引入的逃逸力方向与无人船受到的来自难以避让的阻挡前行物体的排斥力或来自目标点的引力方向垂直,可以视为无人船在逃逸力的作用下脱离正常航行规划轨迹中的局部极小值点,进而朝着目标点继续行进,引入的逃逸力可用如下函数表达式进行计算:
| $ \begin{gathered} \left| {{F_{rx}}_e} \right| = \left\{ {\begin{array}{*{20}{c}} \alpha \left| {{F_{rx}}} \right|*\cos \theta ,&\rho < {\rho _o},\\ 0,&\rho \geqslant {\rho _o} ,\end{array}} \right. \hfill \\ \left| {{F_{rye}}} \right| = \left\{ {\begin{array}{*{20}{c}} \beta \left| {{F_{ry}}} \right|*\sin \theta ,&\rho < {\rho _o},\\ 0,&\rho \geqslant {\rho _o} 。\end{array}} \right. \hfill \\ \end{gathered} $ | (13) |
式(13)描述了坐标轴的X方向和Y方向上逃逸力的分量。逃逸力应视为在该点与斥力合成,形成新的斥力,改变无人船的航向,并从局部极小值点逃逸。其中逃逸力系数分别用
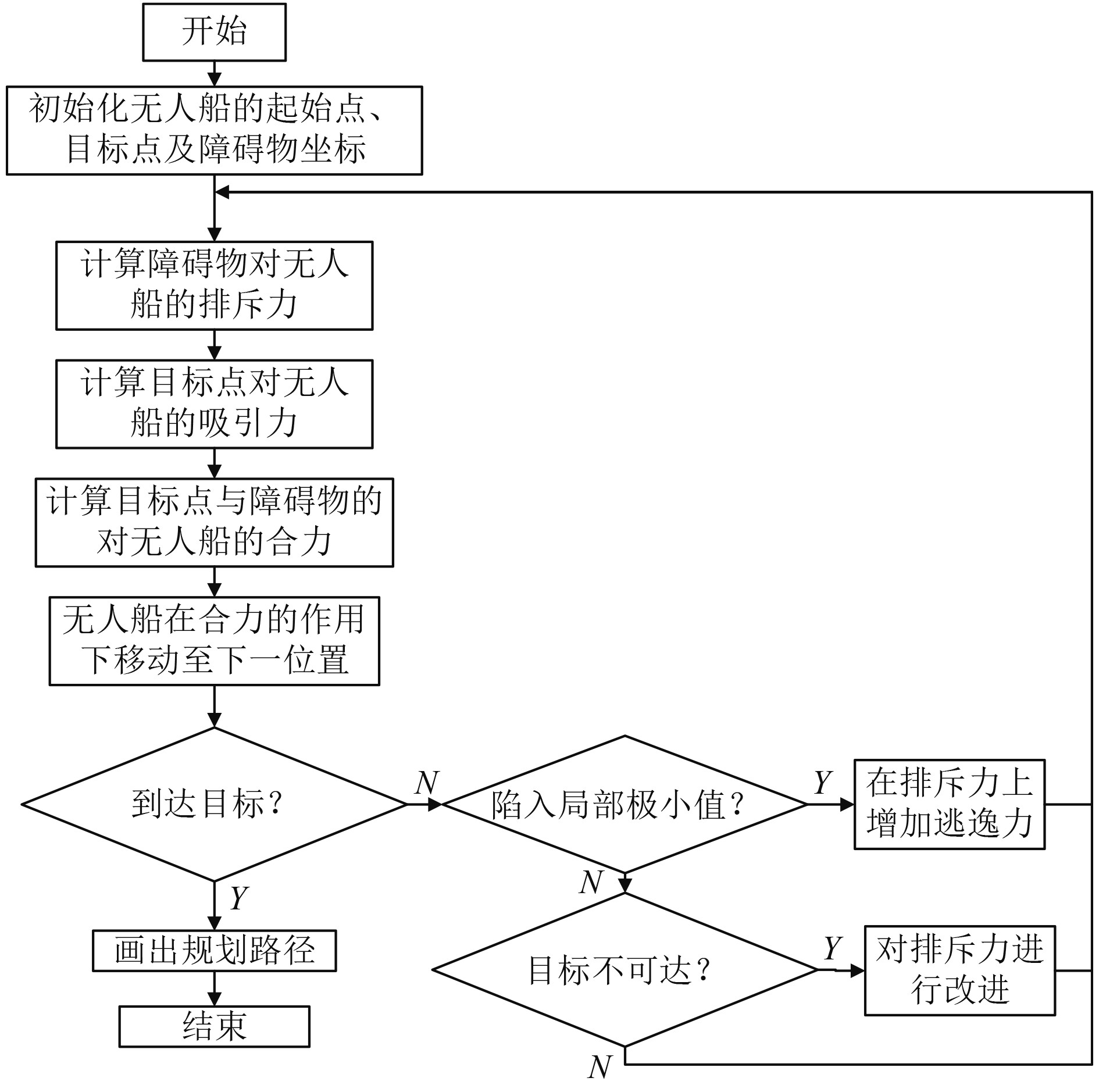
结合提出的改进人工势场算法及逃逸力函数,设计出无人船路径规划的算法流程,具体步骤如图2所示。
|
图 2 改进算法的无人船路径规划流程图 Fig. 2 Flow chart of unmanned ship path planning with improved algorithm |
首先对无人船规划路径的起始点、目标点和障碍物的位置进行初始化。然后,在航行的过程中不断计算来自障碍物的排斥力和目标点对其产生的吸引力,将吸引力与排斥力进行合力计算,引导无人船航进至下一点位。紧接着,判断无人船是否陷入局部最小值,如果无人船无法继续航行,则判定其陷入局部最小值状态,需要增加逃逸力因子使其从当前本地最小值点逃离。如果无人船到达目标点附近,且存在不可达问题,则改变斥力,以获得使无人船正常航进至目标点的合力,实现对无人船完整路径的整体规划[1]。
3 仿真验证为验证本文所提基于改进人工势场算法的无人船路径规划技术的有效性,采用仿真的手段对其进行验证分析。仿真过程中,将无人船的起始点设定为(0,0),无人船的目标点设定为(10,10)。在无人船航行路径规划中,障碍物的影响半径通常定义为障碍物的影响距离[6]。本次模拟仿真过程中,将障碍物的影响半径设定为2 m,即当障碍物到无人船之间的距离小于2 m时,障碍物便会对无人船施加有效的斥力势场[7]。
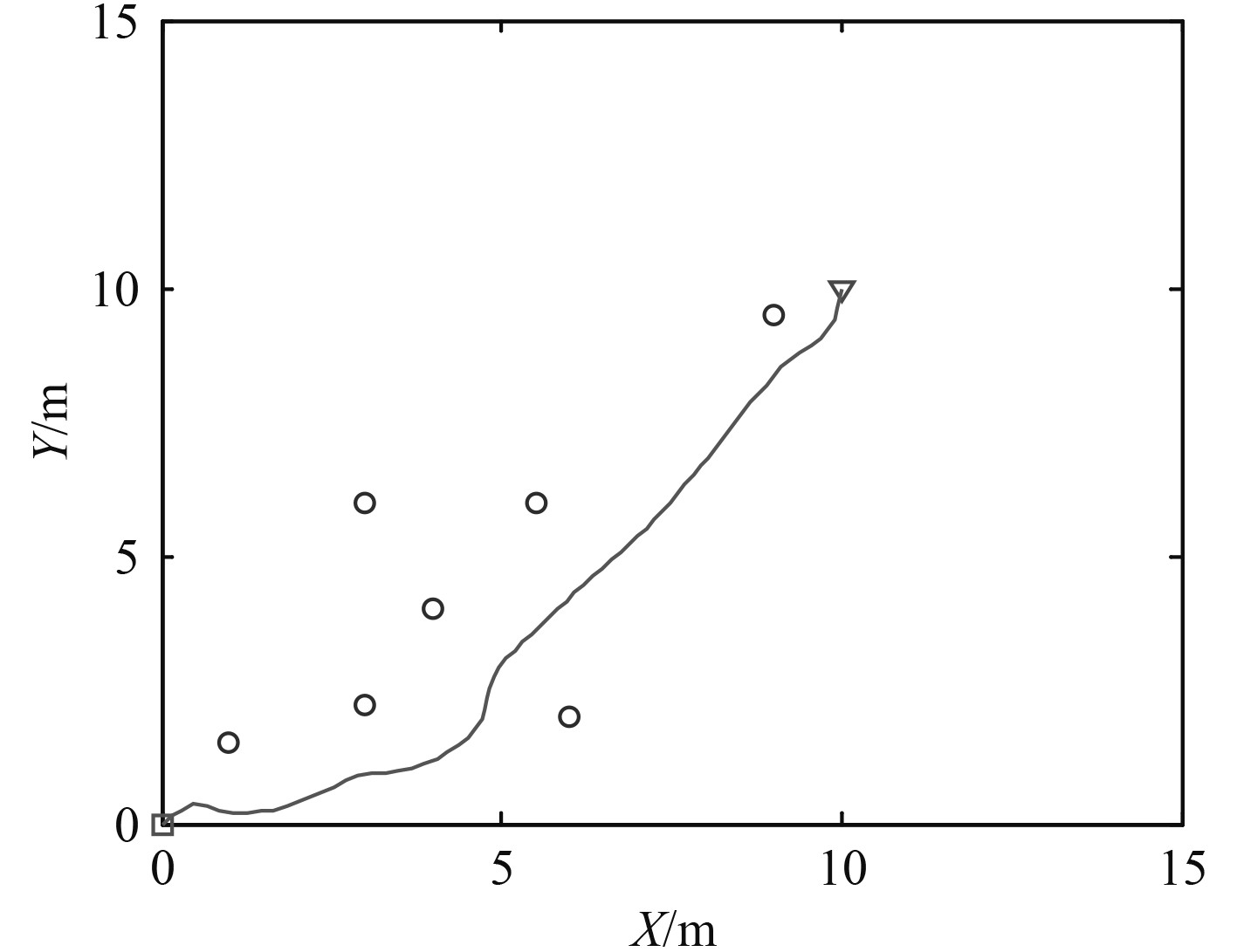
图3为利用Krogh的改进算法,解决目标不可达问题的无人船航进曲线。
|
图 3 Krogh改进的人工势场算法路径规划航进曲线 Fig. 3 Artificial potential field path planning algorithm under Krogh improvement |
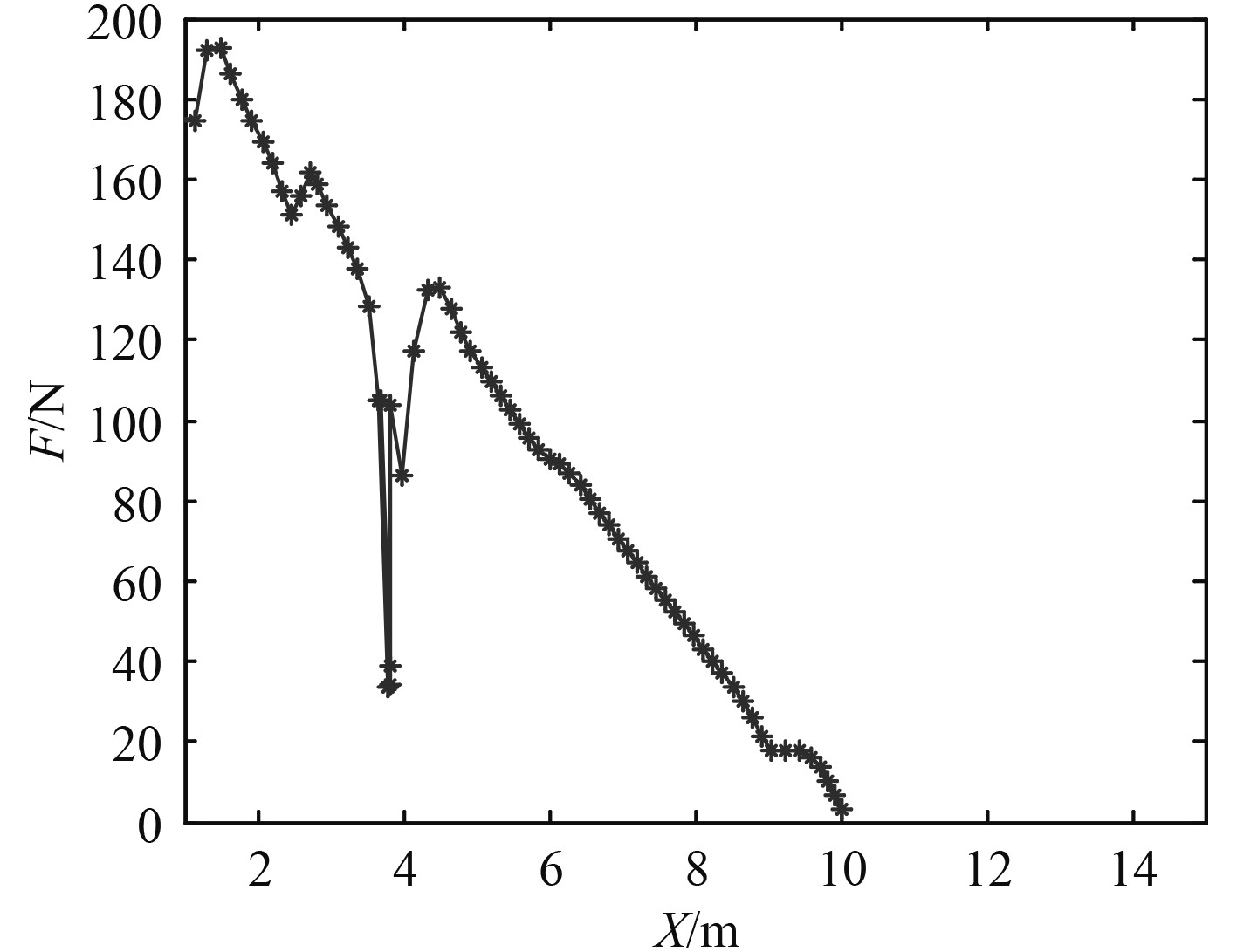
由图3可知,采用Krogh改进的人工势场算法,无人船航行中可有效躲开障碍物,并避免出现目标不可达问题,从而到达目标点。在整个过程中无人船受到的吸引力与排斥力的合力曲线如图4 所示。
|
图 4 Krogh改进的人工势场算法路径规划过程合力曲线 Fig. 4 Krogh's improved artificial potential field path planning process ensemble curve |
由图4可知,基于Krogh的改进人工势场算法,正常航进过程中的无人船受到的作用其上合力变化较大,避障路径随之增长,无人船的航进效率显著降低。
图5描述了在本文改进的人工势场作用下,无人船的路径规划航行轨迹。在此过程中,作用于无人船其上的吸引力与排斥力合成的合力曲线如图6所示。

|
图 5 本文改进算法的无人船路径规划航进曲线 Fig. 5 Improved path planning algorithm for unmanned ships in this paper |

|
图 6 本文改进的人工势场算法路径规划过程合力曲线 Fig. 6 The improved artificial potential field path planning process ensemble curve in this paper |
由图6可知,相比于Krogh算法下无人船受到的合力,本文所述算法的合理作用更为平缓。相比于Krogh算法,本文论述的优化方案作用下,无人船的避障路径更短,避障前提下的航进效率也相应的更为优越[8]。
对于可能存在的局部极小值问题,本文将无人船的运动步长设定为0.1。当无人船2次航进之间的步长小于0.1时,确定其出现局部极小值问题,航进终止。选取逃逸力系数分别为

|
图 7 Krogh改进算法的逃离局部极小值过程 Fig. 7 Escape from local minima process under Krogh's improved algorithm |

|
图 8 Krogh改进算法的逃离局部极小值过程排斥力曲线 Fig. 8 Exclusion force curves for escape from local minimal value processes under Krogh's improved algorithm |
分析图8可以看出,作用于无人船的逃逸力能够满足无人船逃离局部极小值点的需要,但其受到的排斥力远大于实际需要,进而导致避障路径增长的问题出现,避障效率也随之有所下降[9]。
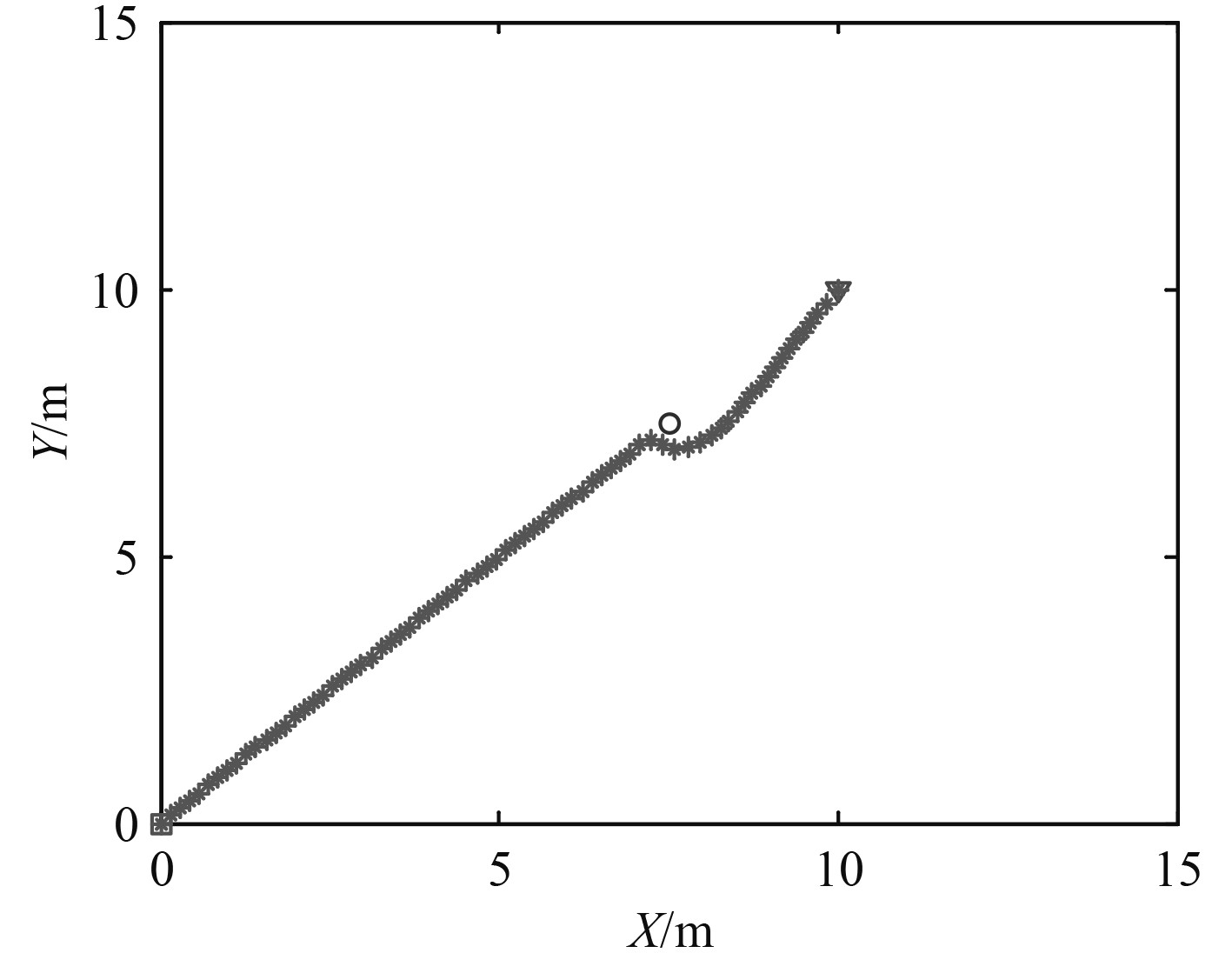
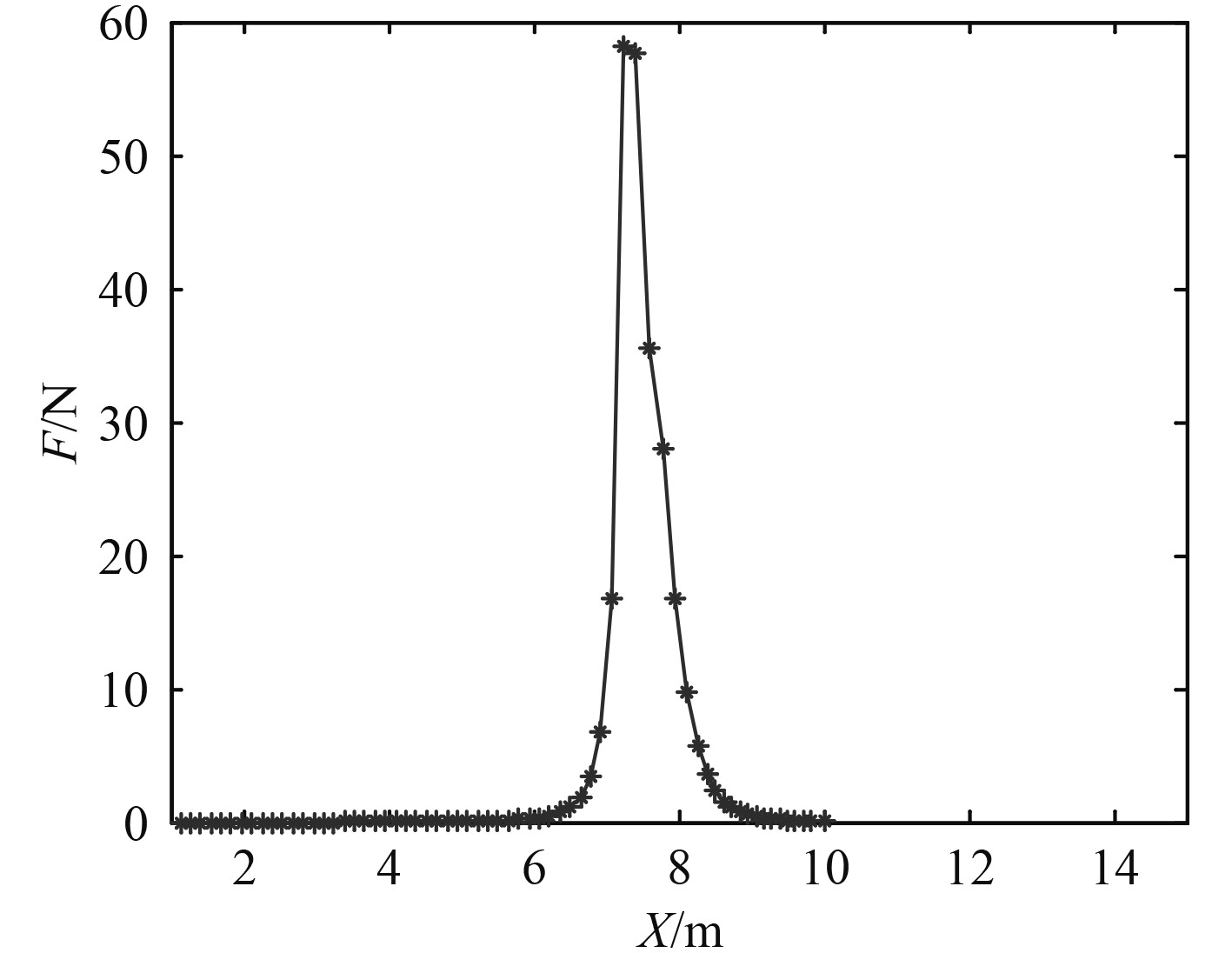
利用本文所述的改进算法,分别绘制无人船逃离轨迹图及作用于其上的排斥力变化图如图9和图10所示。
|
图 9 本文改进算法的逃离局部极小值过程 Fig. 9 The escape from local minima process under the improved algorithm in this paper |
|
图 10 本文改进算法的逃离局部极小值过程排斥力曲线 Fig. 10 The repulsive force curve of escape from local minimal value process under the improved algorithm in this paper |
由图10可知,相较于Krogh算法,本文算法作用下,无人船受到的排斥力相对更小。虽然无人船受到障碍物最大影响范围的约束,但仍能确定出最短的航进路线并抵达终点,此时,无人船已顺利逃离局部最小值点。
为了进一步验证本文改进的人工势场路径规划算法的有效性,利用仿真模拟技术首先对港口的实际结构形式进行了模拟,在此基础上,对无人船离港的最优路径进行了规划,本次模拟过程中,障碍物的影响范围取为2m。利用传统人工势场法,模拟得到无人船的离港路径如图11所示[10]。

|
图 11 传统人工势场算法出海港过程仿真轨迹 Fig. 11 Traditional artificial potential field algorithm out of the harbor process simulation trajectory |
由图11可知,无人船离港过程中,虽然对障碍物进行了有效的一些避让,但在局部的障碍物处产生了航线震荡,航进距离增长。此外,出港经过港口堤坝时,距离堤坝过近,可能导致撞击现象的产生[11]。
图12描述了在本文改进的人工势场算法作用下,无人船驶出港口的过程。分析可知,经过改进的算法,可以使得无人船航进方向更为稳定,虽然由此造成了航进里程的增加,但其在穿越港口堤坝时的位置更为居中,基本不会存在与堤坝发生碰撞的可能,安全性大幅度提升。因此本文的研究具有实际意义[12]。

|
图 12 本文改进人工势场算法出海港过程仿真轨迹 Fig. 12 This paper improves the artificial potential field algorithm out of the harbor process simulation trajectory |
本文通过对Krogh算法的优化,同时提出一种改进人工势场函数,解决了传统的人工势场算法在无人船路径规划中出现的目标不可达问题以及局部极小值问题;在优化过程中增加了逃逸力因数,使无人船在遇到局部极小值问题时,可在逃逸力的作用下逃离局部极小值点[13]。改进后的人工势场算法可以使无人船有效规避障碍物,安全到达目标点[14]。无人船出港口的仿真实验验证了改进人工势场算法的有效性,与传统人工势场法的仿真结果进行对比,可以发现改进后的人工势场法应用于无人船的航行轨迹规划,使得无人船的航行过程中,规避障碍物变得更加灵活,规划的航行轨迹更加能符合实际航行需求。
| [1] |
栾天宇. 无人船自动驾驶系统的设计与实现[D]. 北京: 北京理工大学, 2018.
|
| [2] |
陈永泽, 舒军勇, 王真亮, 等. 基于GPS定位的无人艇自主导航[J]. 重庆理工大学学报, 2016, 30(8): 117-121. |
| [3] |
田勇. 水面无人艇运动控制系统设计与实现[D]. 大连: 大连海事大学, 2016.
|
| [4] |
石祥. 水面无人船控制系统设计与研究[D]. 上海: 上海海洋大学, 2015.
|
| [5] |
ADVISOR P, SHOCKEY I. A study of the feasibility of autonomous surface vehicles[J]. Journal of Marine Science and Application, 2013, 1-4. |
| [6] |
李明. 智能车辆避障路径规划及横向控制研究[D]. 大连: 大连理工大学, 2013.
|
| [7] |
LI Ronghui, QI Yunpeng, LI Tieshanet al. On path following of underactuated surface ships[M]. Norway, 2009: 751-756.
|
| [8] |
Fossen Thor I. , Guidance and control of ocean vehicles[M]: Norway, 1994
|
| [9] |
廖煜雷. 无人艇的非线性运动控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [10] |
邵峰. 双体双推进无人船路径跟踪控制研究[D]. 青岛: 青岛大学, 2015.
|
| [11] |
张新慈. 基于ROS的无人水面艇运动控制系统的设计[D]. 南京: 江苏科技大学, 2015.
|
| [12] |
Bertram Volker. Unmanned surface vehicles–a survey[J]. Skibsteknisk Selskab, 2008, 1-4. |
| [13] |
苏金涛. 无人水面艇路径规划[J]. 指挥控制与仿真, 2015(6): 36-40. DOI:10.3969/j.issn.1673-3819.2015.06.008 |
| [14] |
卢艳爽. 水面无人艇路径规划算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
 2022, Vol. 44
2022, Vol. 44

