三体船是一种高性能船舶,区别于传统大型船舶,三体船型在流体动力学和空气动力学方面具有更高的性能,可以获得更快的速度和更高的稳定性。
三体船型由主船体和两侧子船体组成,主船体尺寸与规格较大,为三体船提供静止状态和高速航行状态下的浮力,主船体的长宽比相对较大,船体底部的斜升角较小,可以在高速航行时获得足够的水动升力和气动升力;子船体呈对称分布,与主船体刚性连接,形成的攻角为负值,在降低三体船空气阻力的同时,保证三体船在高速航行状态下的姿势调节[1]。
本文对三体船的阻力特性和运动性能进行分析,建立三体船的运动坐标系,结合有限元分析技术和CFD计算流体力学理论,分别对三体船在水面上的自由液面处理、有限元网格的收敛特性、有限元仿真的边界条件等内容进行详细研究。
1 三体船的运动坐标系建立及基本CFD理论计算流体动力学CFD是流体动力学和数值计算相结合的产物,CFD利用有限元分析的思想,将空间中的流体和分析目标进行有限元化,并建立这些有限元之间的数学方程组,通过求解有限元方程,获取目标的流体动力学参数,常用的CFD分析软件有Fluent,STAR-CCM+等。
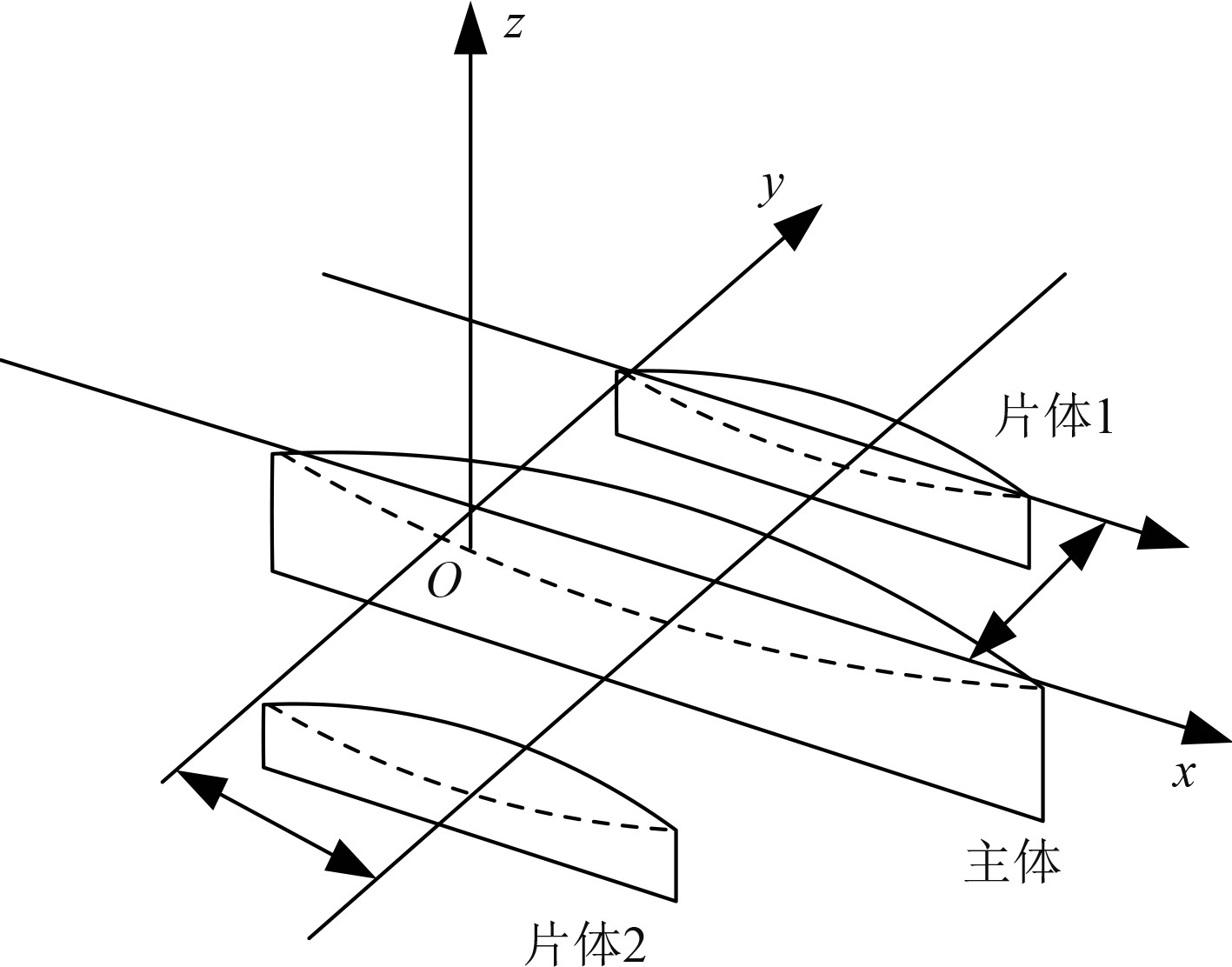
在进行三体船的阻力和运动性能分析前,需要根据三体船的结构与运动特性进行CFD建模,首先建立三体船的运动坐标系如图1所示。
|
图 1 三体船运动坐标系 Fig. 1 Trimaran motion coordinate system |
如图,三体船的运动速度方向为OX正向,OY方向与三体船的左舷方向重合,OZ方向指向三体船的垂向,三体船在流体中的速度势
| $ {\Delta ^2}\psi {\text{ = }}0 \text{,} $ |
建立三体船的动量方程如下:
| $ m\frac{{\partial \left( {\rho {u_x}} \right)}}{{\partial t}} + m\frac{{\partial \left( {\rho {u_x}{u_y}} \right)}}{{\partial t}} = m\frac{\partial }{{\partial t}}\left[ {\mu \left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right)} \right] + {F_i} \text{。} $ |
式中:
船舶计算流体力学是建立在流体力学基本方程的基础上的,假设海水不可压缩,则建立海水的连续性方程为:
| $ \rho * \frac{{{\rm{d}}V}}{{{\rm{d}}t}} + \frac{{\delta \left( {\rho l} \right)}}{{\delta y}} + \frac{{\delta \left( {\rho m} \right)}}{{\delta z}} + \frac{{\delta \left( {\rho n} \right)}}{{\delta x}} = 0 \text{。} $ |
式中:
流体的湍流模型如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\partial l}}{{\partial t}} + {m_0}\dfrac{{\partial m}}{{\partial {t_{}}}} = \dfrac{\partial }{{\partial y}}\left[ {\left( {v + {\sigma _k}l} \right)\dfrac{{\partial n}}{{\partial t}}} \right] + {\beta ^*} \times {P_k}},\\ {\dfrac{{\partial {P_k}}}{{\partial t}} = \dfrac{\partial }{{\partial t}}\left[ {\left( {V + {\sigma _k}l} \right)\dfrac{{\partial m}}{{\partial t}}} \right] + 2(1 - {F_i})} 。\end{array}} \right. $ |
式中:
在三体船的阻力及运动分析过程中,自由液面的处理是非常关键的步骤,常用的自由液面处理方法有势流理论法和VOF法[2],其中,势流理论法在处理船舶流体动力学问题时,能够较好地拟合船首和船舶周围较远流场的动力学特性,当在处理船尾及船舶近场流体特性时精度较低,因此,本文使用VOF法进行船体自由液面的处理。
设三体船的流体计算域为V,流体A所在的区域为
| $ \alpha \left( {x,t} \right) = \left\{ \begin{gathered} 0,\;\;x \in {V_1} ,\hfill \\ 1,\;\;\;x \in {V_2},\hfill \\ \end{gathered} \right. $ |
式中,
| $ \frac{{\partial \alpha }}{{\partial t}} + u\frac{{\partial \alpha }}{{\partial x}} + v\frac{{\partial \alpha }}{{\partial y}} + w\frac{{\partial \alpha }}{{\partial z}} = 0 \text{,} $ |
利用有限元分析思路,将自由液面划分为有限个网格单元
| $ {\varphi _{}} = \frac{1}{{\Delta {V_{ij}}}}\int_{{V_{}}} \alpha (x,t){\rm{d}}V \text{,} $ |
可得流体A的VOF函数满足:
| $ \frac{{\partial \varphi }}{{\partial t}} + u\frac{{\partial \varphi }}{{\partial x}} + v\frac{{\partial \varphi }}{{\partial y}} + w\frac{{\partial \varphi }}{{\partial z}} = 0 。$ |
当
|
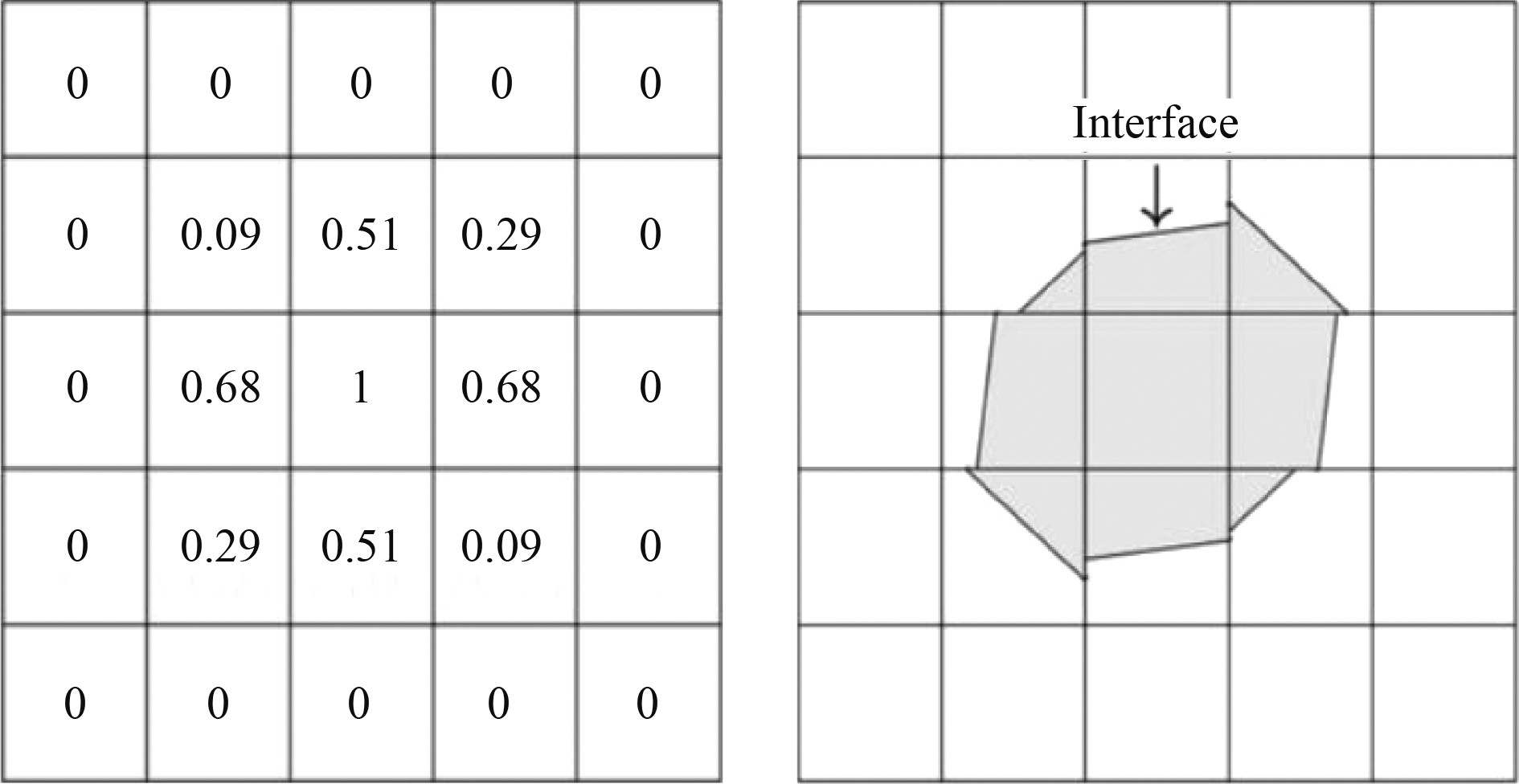
图 2 VOF函数及自由液面interface示意图 Fig. 2 Schematic diagram of VOF function and free surface interface |
根据流体的VOF函数
| $ \int\limits_S {\frac{\partial }{{\partial {t^{}}}}\left( {{\rho _0}\varphi } \right){\rm{d}}V + \int\limits_{}^{} {div\left( {{\rho _0}\bar \varphi } \right){\rm{d}}V} = } S\left( V \right) \text{,} $ |
建立流场的湍流模型为:
| $ {\rho _0}\frac{{{\rm{d}}\frac{1}{2}{{\bar u}_i}}}{{{\rm{d}}t}} = \frac{\partial }{{\partial t}}\left\{ {\frac{{\delta {{\bar u}_i}}}{{\delta t}}} \right\} - {\rho _0}\varepsilon 。$ |
式中:
利用计算流体力学软件STAR-CCM+软件[4]进行三体船的船型阻力及运动性能分析,主要对STAR-CCM+软件中三体船及周围流场的有限元建模进行研究。
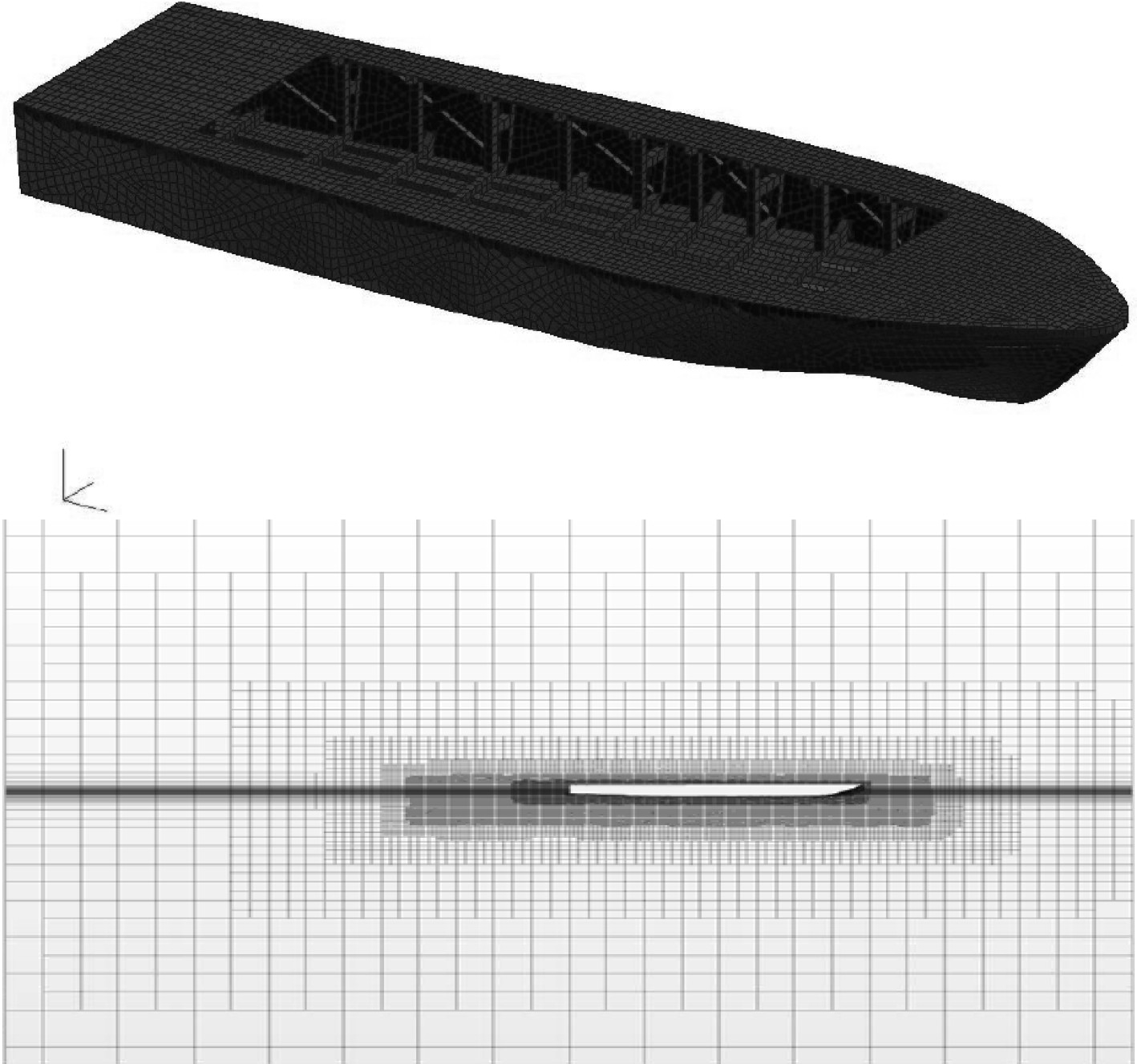
在STAR-CCM+软件中,有限元模型的网格收敛是保证计算精度的重要指标。使用广义RE法进行网格收敛判断,首先建立船体及船舶周围流场的有限元模型如图3所示。
|
图 3 船体及船舶周围流场的有限元模型 Fig. 3 Finite element model of flow field around hull and ship |
将网格的细化率
| $ \begin{gathered} {\tau _1} = {S_1} - {S_2},\hfill \\ {\tau _2} = {S_2} - {S_3},\hfill \\ \end{gathered} $ |
可得有限元模型的收敛率[5]为:
| $ \kappa = \frac{{{\tau _1}}}{{{\tau _2}}} 。$ |
当
建立的三体船及流场有限元模型中,网格的收敛率为:
| $ {\kappa _o} = \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \frac{{0.000\;086}}{{0.000\;127}} = 0.677 \text{,} $ |
有限元模型的模拟精度为:
| $ {P_G} = \frac{{\ln \left( {{\varepsilon _2}/{\varepsilon _1}} \right)}}{{\ln \kappa }} = 1.025 \text{。} $ |
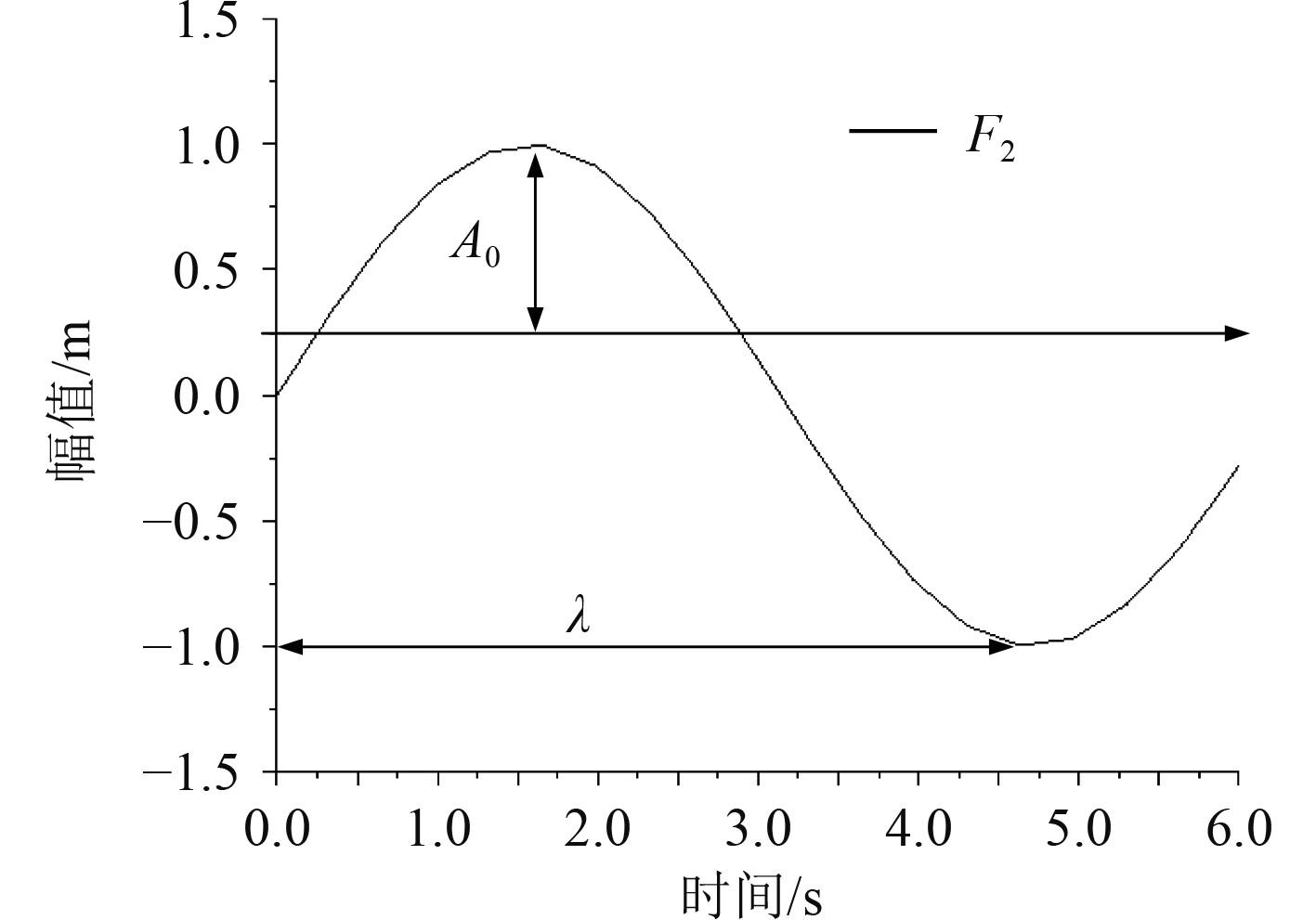
在STAR-CCM+软件中定义三体船阻力及运动流体力学分析的边界条件,其中,波浪特性是影响三体船运动特性的关键因素,本文将海浪简化为余弦规则波,如图4所示。
|
图 4 海浪余弦规则波示意图 Fig. 4 Schematic diagram of wave cosine regular wave |
海浪的波形函数[6]如下:
| $ \xi(t)=\sum_{i=1}^{n} \xi \cos \left(k \psi \pm \omega t+\varepsilon_{i}\right) 。$ |
式中:
采用的三体船CFD仿真模型参数如表1所示。
|
|
表 1 三体船CFD仿真模型参数表 Tab.1 Parameter table of trimaran CFD simulation model |
软件定义的前7个仿真工况中,波浪的波长、波幅以及海浪频率的变化范围[7]如表2所示。
|
|
表 2 前7个仿真工况的波浪参数 Tab.2 Wave parameters of the first seven simulation conditions |
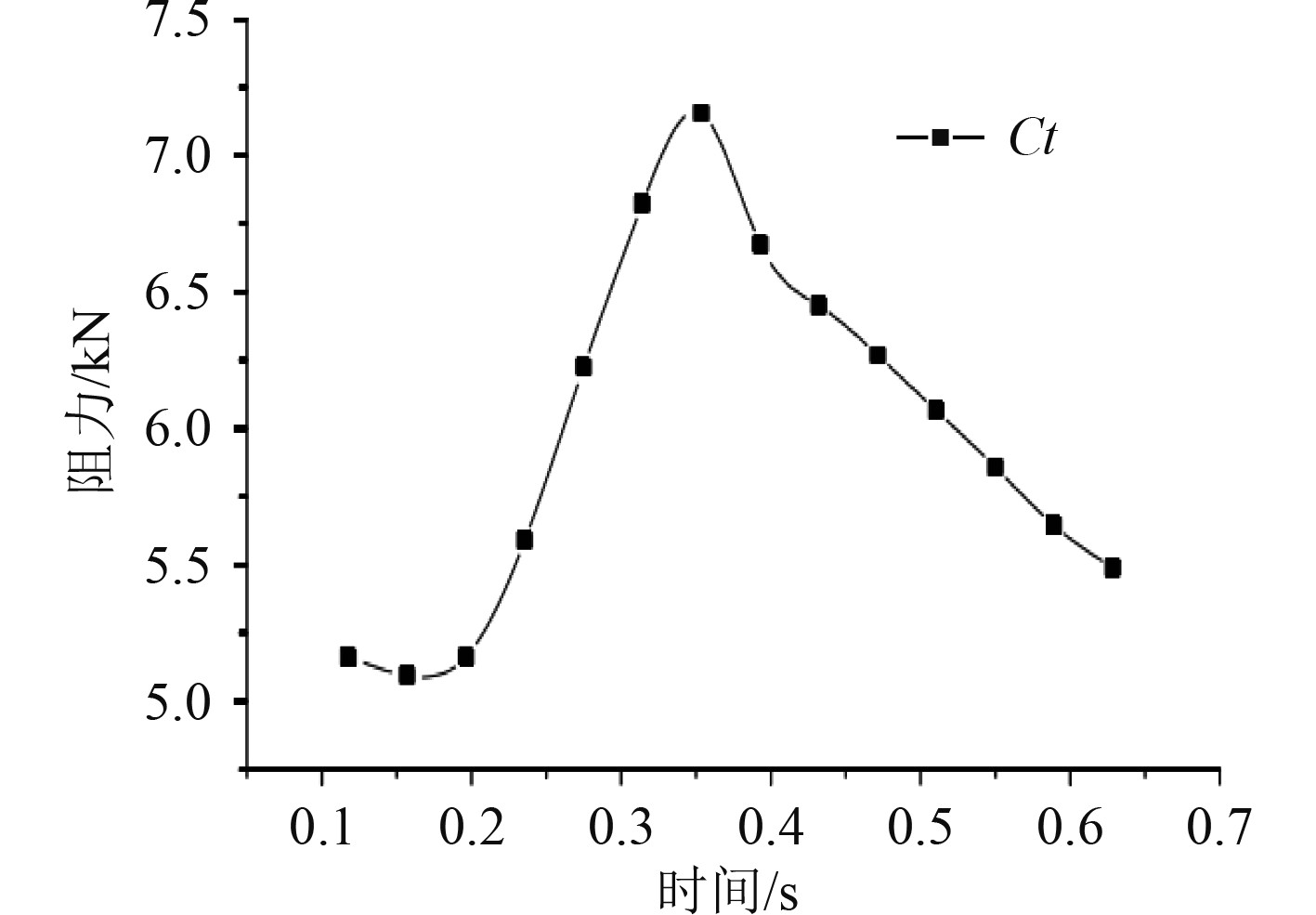
得到航速一定下的三体船阻力特性变化曲线如图5所示。
|
图 5 航速一定下的三体船阻力特性变化曲线 Fig. 5 Resistance characteristic curve of trimaran at a certain speed |
三体船作为一种高速船舶,在设计过程中需要重点考虑其流体动力学特性,本文以计算机流体力学软件STAR-CCM+为工具,通过三体船运动建模、VOF自由液面建模以及有限元模型的收敛特性分析,进行三体船的阻力特性仿真。
| [1] |
陈京普, 朱德祥, 何术龙. 双体船/三体船兴波阻力数值预报方法研究[J]. 船舶力学, 2006, 10(2): 7. |
| [2] |
卢晓平, 郦云, 董祖舜. 高速三体船研究综述[J]. 海军工程大学学报, 2005, 17(2): 7. |
| [3] |
欧阳宽, 陈明华, 王固祺, 等. 高速三体船於环流水槽实验之阻力性能探讨[J]. 台北海洋技术学院学报, 2012, 5(1): 61-77. |
| [4] |
李培勇, 裘泳铭, 顾敏童, 等. 超细长三体船耐波性试验研究[J]. 海洋工程, 2002, 20(4): 5. DOI:10.3969/j.issn.1005-9865.2002.04.002 |
| [5] |
郦云, 卢晓平. 高速三体船阻力性能研究[J]. 船舶力学, 2007, 11(2): 8. |
| [6] |
吴广怀, 吴培德, 蒋耀军, 等. 基于兴波阻力的三体船片体位置快速优化方法[J]. 船舶力学, 2005, 9(4): 8. |
| [7] |
卢晓平, 王中, 孙永华, 等. Rankine源Dawson型方法求解三体船兴波阻力[J]. 华中科技大学学报:自然科学版, 2008, 36(11): 5. |
 2022, Vol. 44
2022, Vol. 44
