2. 福建省船舶与海洋工程重点实验室,福建 厦门 361021;
3. 空军装备部驻西安地区第八军事代表室,陕西 西安 710000
2. Fujian Provincial Key Laboratory for Naval Architecture and Ocean Engineering, Xiamen 361021, China;
3. The Eighth Military Representative Office in Xi′an Area of Air Force Equipment Department, Xi'an 710000, China
先进复合材料作为具有重量轻、比强度/比刚度高、耐腐蚀、抗疲劳、绝缘、无磁、吸/透波性好以及可设计性强等一系列优势,在船舶领域的应用逐渐增多[1-3]。复合材料板架结构作为轻量化船舶的重要组成部分,是船体结构中最常见的单元之一[4],其设计合理与否对船舶本身的安全性和经济性十分重要,是复合材料船舶设计之初乃至整个服役周期都要考虑的重要问题。
考虑到重量、成本、功能、美观等因素,复合材料板架通常设计成薄壁开孔结构,构件的剖面尺寸相对减小,刚度相对降低,容易发生屈曲破坏,复合材料开孔板架在满足其他要求的同时,稳定性问题日益突出,受到高度重视。近年来复合材料船舶板架结构的稳定性研究和优化设计等取得了一定的成果[1, 5-6],但多侧重力学性能和几何尺寸优化等单方面研究,仍需从二者有机结合的角度进一步深化分析。结构的重量最轻或造价最低是优化设计追求的经济性目标,满足稳定性要求是一个重要的约束条件,也可作为设计者追求的安全性目标。在复合材料船舶的优化设计阶段考虑板架结构的稳定性问题,不仅有助于船体局部结构强度的设计分析,而且对船舶在不同工况下总体强度的设计和校核也十分重要。
为此,本文综合考虑复合材料开孔板架结构的稳定性和轻量化问题,采用先进的优化方法和数值计算手段,对典型的复合材料船舶开孔板架进行优化设计。通过板架结构的静力学计算、特征值屈曲分析和响应面优化设计,评估面板厚度、开孔尺寸,加强筋间距、宽度、高度以及厚度等参数的变化对结构整体临界屈曲载荷和重量的影响,进而获得承载结构设计过程中重量较小化且抗屈曲能力较强的最佳设计方案,为复合材料船舶板架结构的设计优化提供参考。
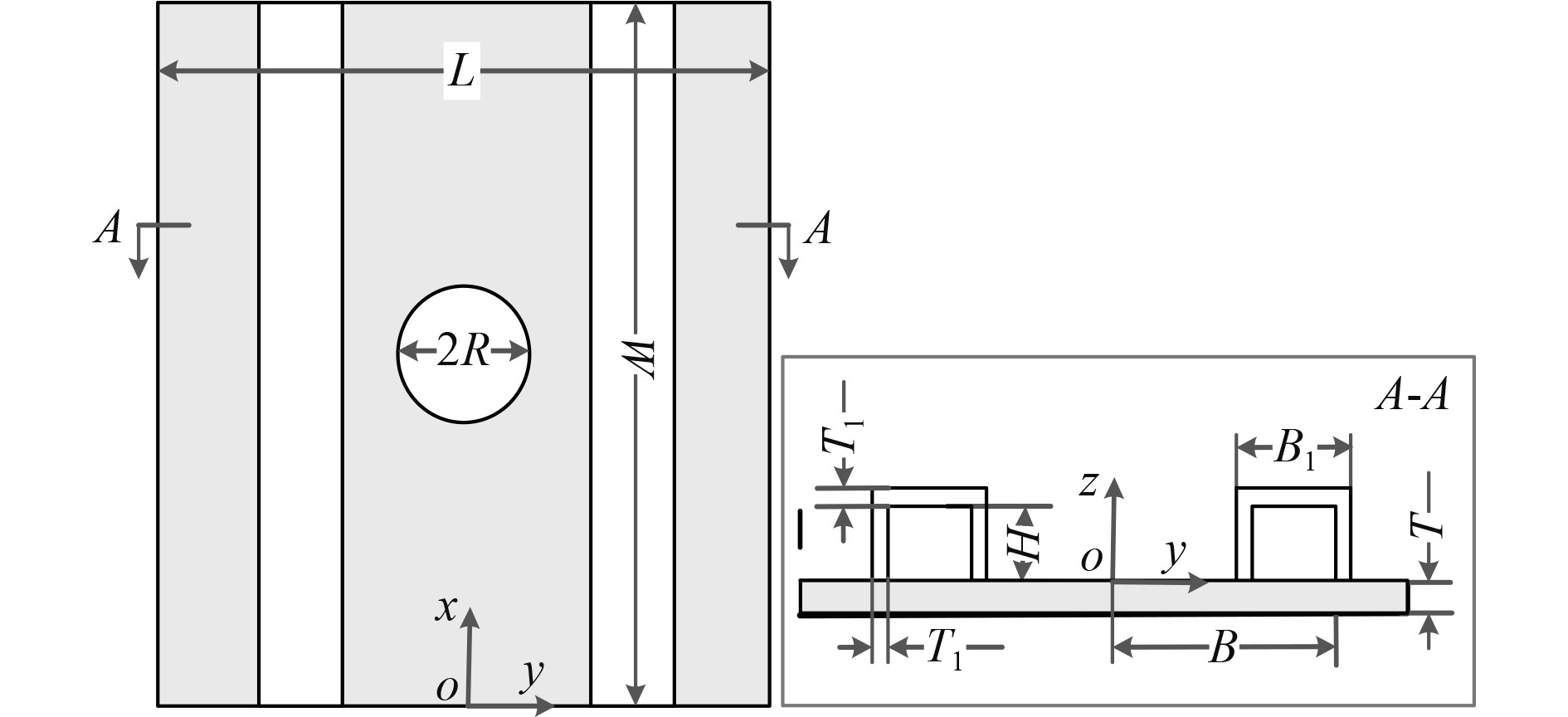
1 复合材料船舶板架设计方案 1.1 几何与材料模型研究构成复合材料船舶的最典型结构单元,该板架结构由1块开孔面板和2根加强筋组成,常见于甲板、舷侧、舱壁等船体结构的重要位置,具体的尺寸参数和材料性能参见图1、表1及表2。
|
图 1 复合材料开孔板架几何构型及尺寸参数 Fig. 1 Geometry and parameters of the composite perforated panel |
|
|
表 1 复合材料开孔板架的几何尺寸 Tab.1 Dimensions of the composite perforated panel |
|
|
表 2 复合材料板架的材料特性 Tab.2 Material properties of the composite perforated panel |
考虑到复合材料板架在船体结构中的位置和作用,以舷侧开孔板承受压缩载荷为例设计边界条件,即开孔板架一端刚固,另一端受到沿着x轴方向的压力,其余两边为自由边。具体的边界条件为:x=0处,ux/y/z=θx/y/z=0;x=L处,uy/z=θx/y/z=0。其中,ux/y/z和θx/y/z分别代表全局坐标系(x,y,z)下的位移自由度和旋转自由度。
2 船舶复合材料板架优化设计结构优化的基本原理是通过构建优化模型,选用合适的优化方法,在一定的约束条件下进行优化迭代计算,求得优化目标的理论极值,进而得到结构的最佳设计方案。
2.1 优化模型 2.1.1 目标函数目标函数是用来衡量设计好坏的指标。采用何种指标来反映设计好坏与结构本身的技术经济特性有关。通常采用的目标函数有:结构的重量、体积和造价3种。结构重量是复合材料船舶开孔板架优化设计的重要指标之一,且比较容易写成设计变量的函数形式。开孔板架的稳定性也是影响船体结构安全性的重要问题,故以板架重量较小且抗屈曲能力较强作为优化目标。
2.1.2 设计变量设计变量指在设计过程中所要选择的描述结构特性的物理量,分为连续设计变量和离散设计变量。复合材料开孔板架的主要几何参数有面板厚度、开孔半径,帽型梁的宽度、高度、厚度,以及约束帽型梁位置的梁间距。这些参数在船舶设计建造过程中是一系列有规律的离散变量。
2.1.3 约束条件结构优化的约束条件一般有几何约束条件和性态约束条件2种。船舶复合材料开孔板架结构的优化设计必须满足几何尺寸约束条件及结构整体约束条件。具体设计变量的约束范围如表3所示。
|
|
表 3 复合材料开孔板架约束条件 Tab.3 Constraint conditions of the composite perforated panel |
响应面法(RSM)是Box等[7]提出的一种试验设计方法,通过回归方程拟合全局范围内多个因素与响应值之间的函数关系,进而寻求最优的设计参数,是一种能够解决多变量问题的综合了试验设计和数学建模的优化方法[8]。
响应面法通过对指定设计空间内的样本点集合进行试验设计,拟合出系统响应值的全局逼近结果来代替真实的响应面。在工程优化设计中,应用响应面法不仅可以得到响应目标与设计变量之间的变化关系,而且不用完全运行整个求解过程就可以输出参数的近似值,使目标函数达到最优。在结构工程领域,响应面法主要应用于结构优化设计和可靠性分析等方面,作为一种近似的计算方法,在过去的十几年中得到了迅速的发展和应用。目前,响应面法已应用于大型船舶的结构优化中[9]。
2.3 优化流程基于Ansys Workbench 2020 R2计算平台进行复合材料船舶开孔板架结构的优化分析,主要涉及几何模型设计、力学性能仿真以及结构优化3个部分。
1)在Workbench设计模块中进行参数化建模,把参与优化的几何参数定义为设计变量,为后续模型修正、数据交互提供可能;
2)在仿真模块中对参数化板架模型开展CAE计算,进行加载、求解,完成静力学分析和特征值屈曲分析,同时将板架重量和临界屈曲载荷定义为设计变量;
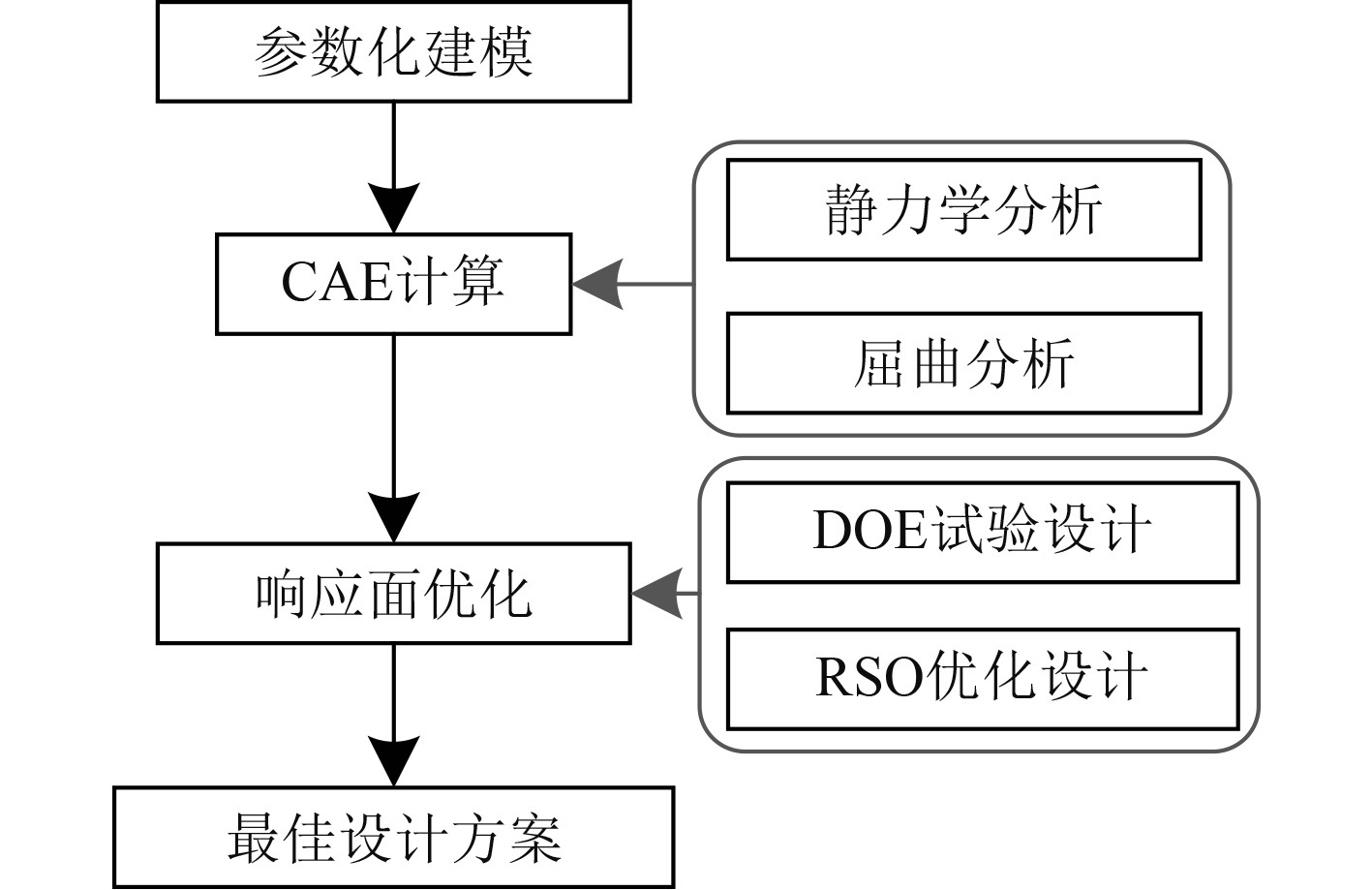
3)响应面优化设计,通过DOE试验设计和RSO响应面优化确定了复合材料开孔板架的最佳设计方案。其中,采用最优空间填充设计确定采样点的位置;使用基因聚合法拟合构造标准三维响应曲面和二维设计曲线;应用多目标遗传算法,生成6000个初始样本点,每次迭代产生1200个样本,经14118次迭代评估后收敛,获得最佳设计方案。具体流程如图2所示。
|
图 2 优化流程图 Fig. 2 Optimization flow chart |
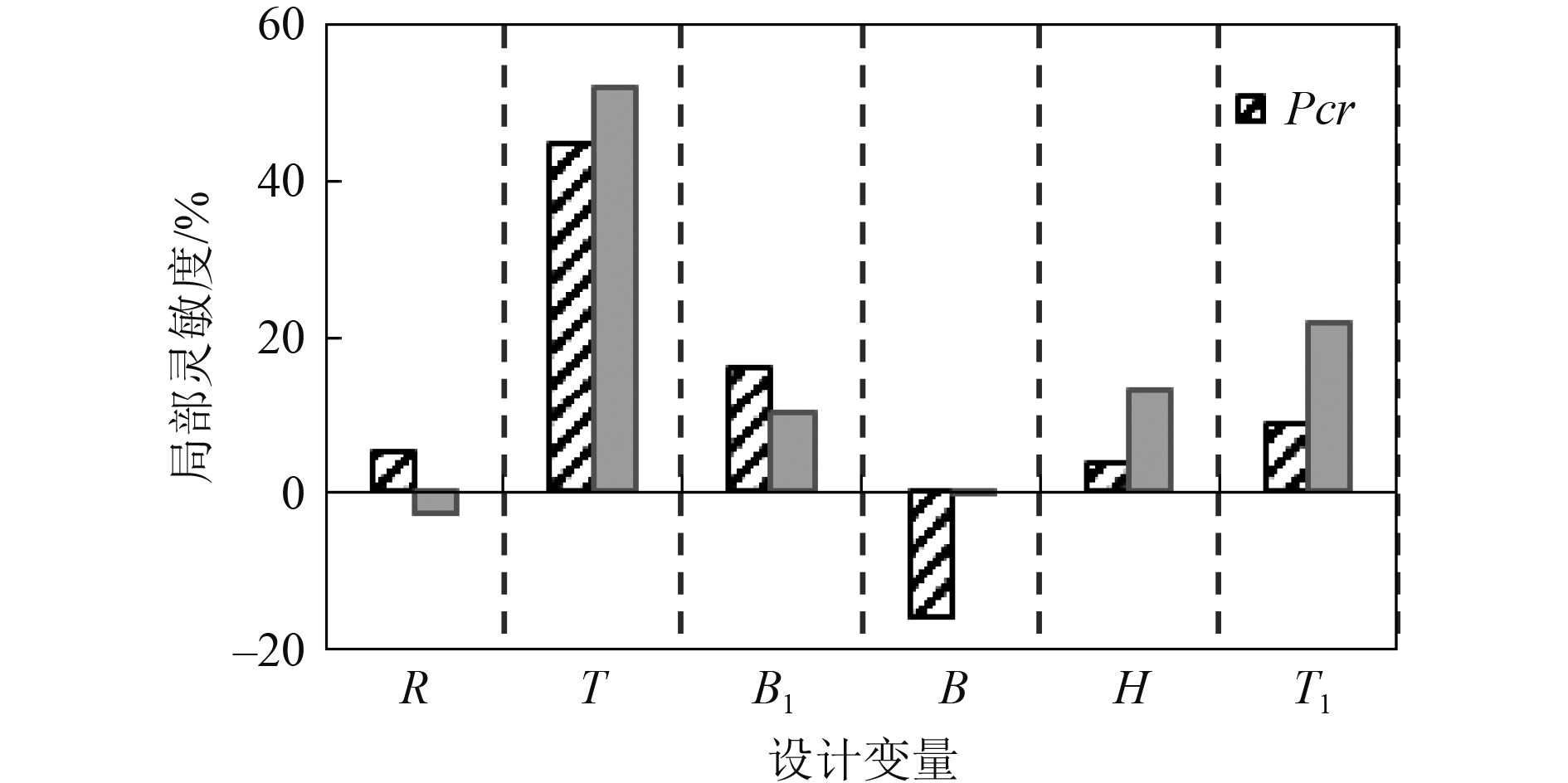
由图3的局部灵敏度可见,开孔板架的临界屈曲载荷Pcr受5个设计变量的正影响,在响应点的局部范围内,其影响程度关系是T>B1>T1>R>H,且Pcr随这5个参数的增加而增大;设计变量B对Pcr产生负影响,Pcr随帽型梁间距的增大而减小。板架重量m主要受参数T和T1的影响,其次是参数H和B1,在响应点局部范围内m随这些变量的增大而增加。参数B与重量m无关,其灵敏度为0。变量R对m具有负影响,开孔越大板架重量越小。板架重量和临界屈曲载荷均随变量T、T1、B1和H的增加而增大,这几个变量确定时要在重量最小和稳定性最好之间做有效权衡;变量B对重量无影响,仅以稳定性最好为目标筛选取值。变量R对Pcr和m的影响相反,该参数取值需针对优化目标寻找合适的折中点。
|
图 3 局部灵敏度 Fig. 3 Local sensitivity |
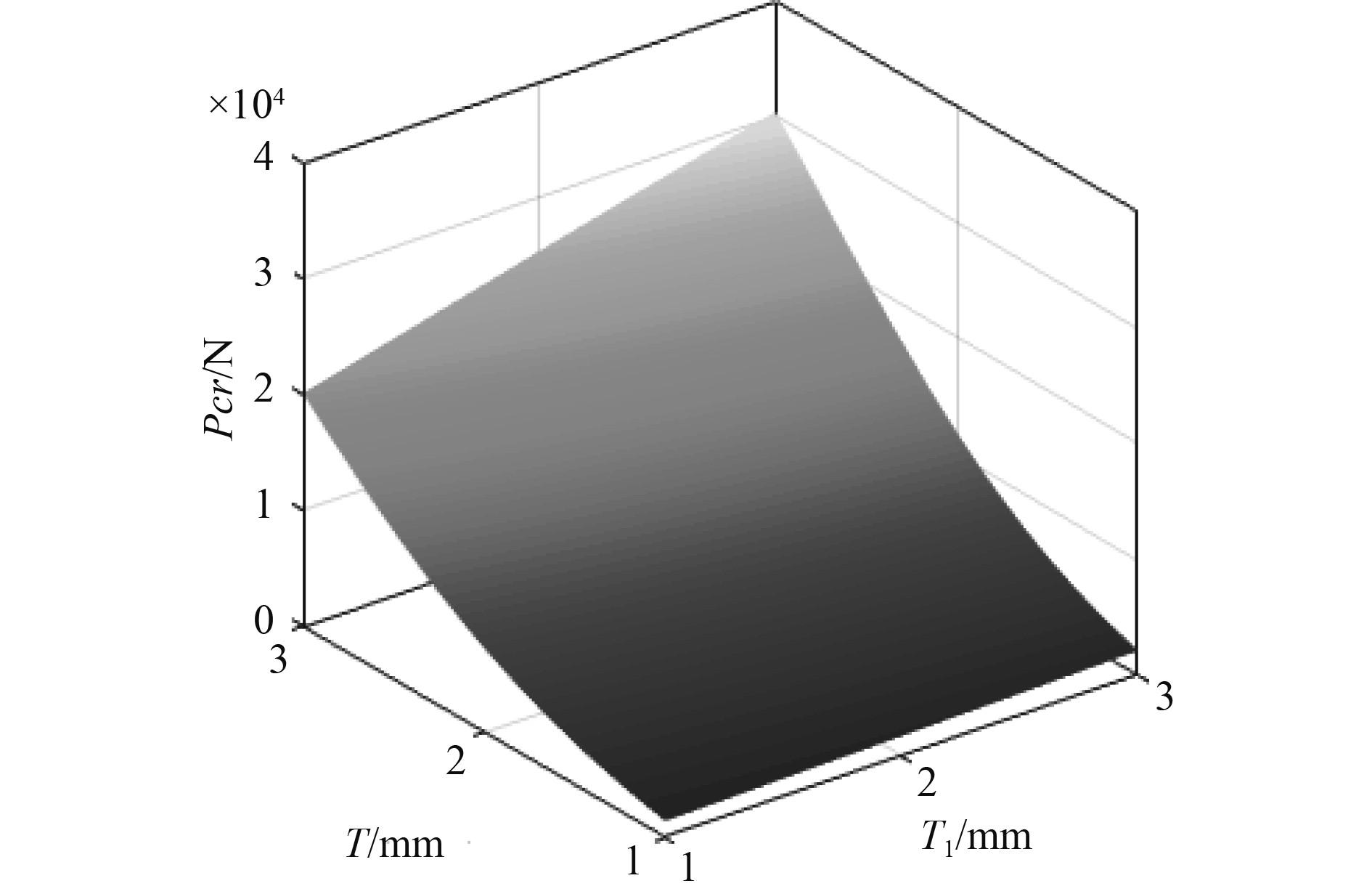
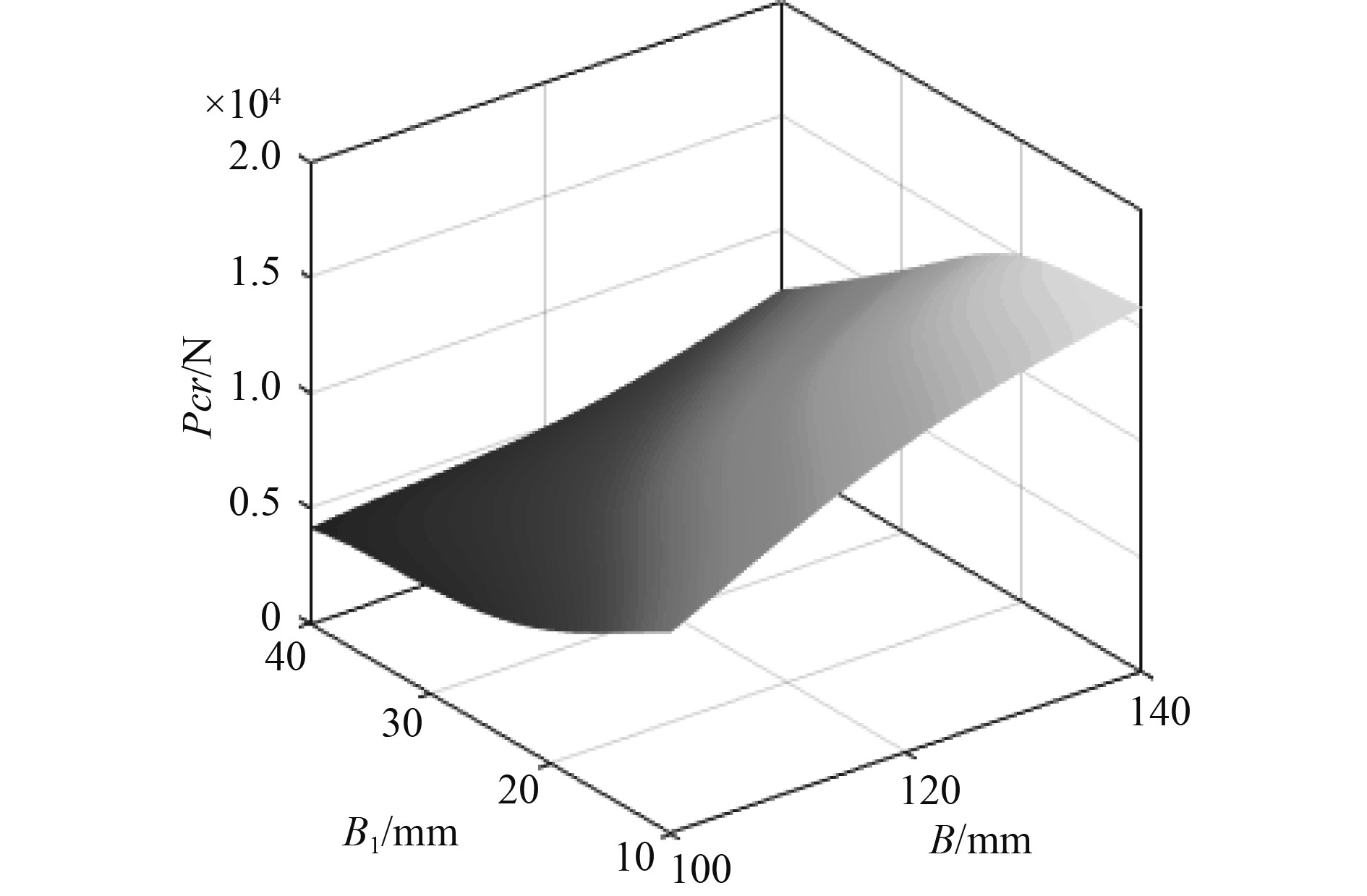
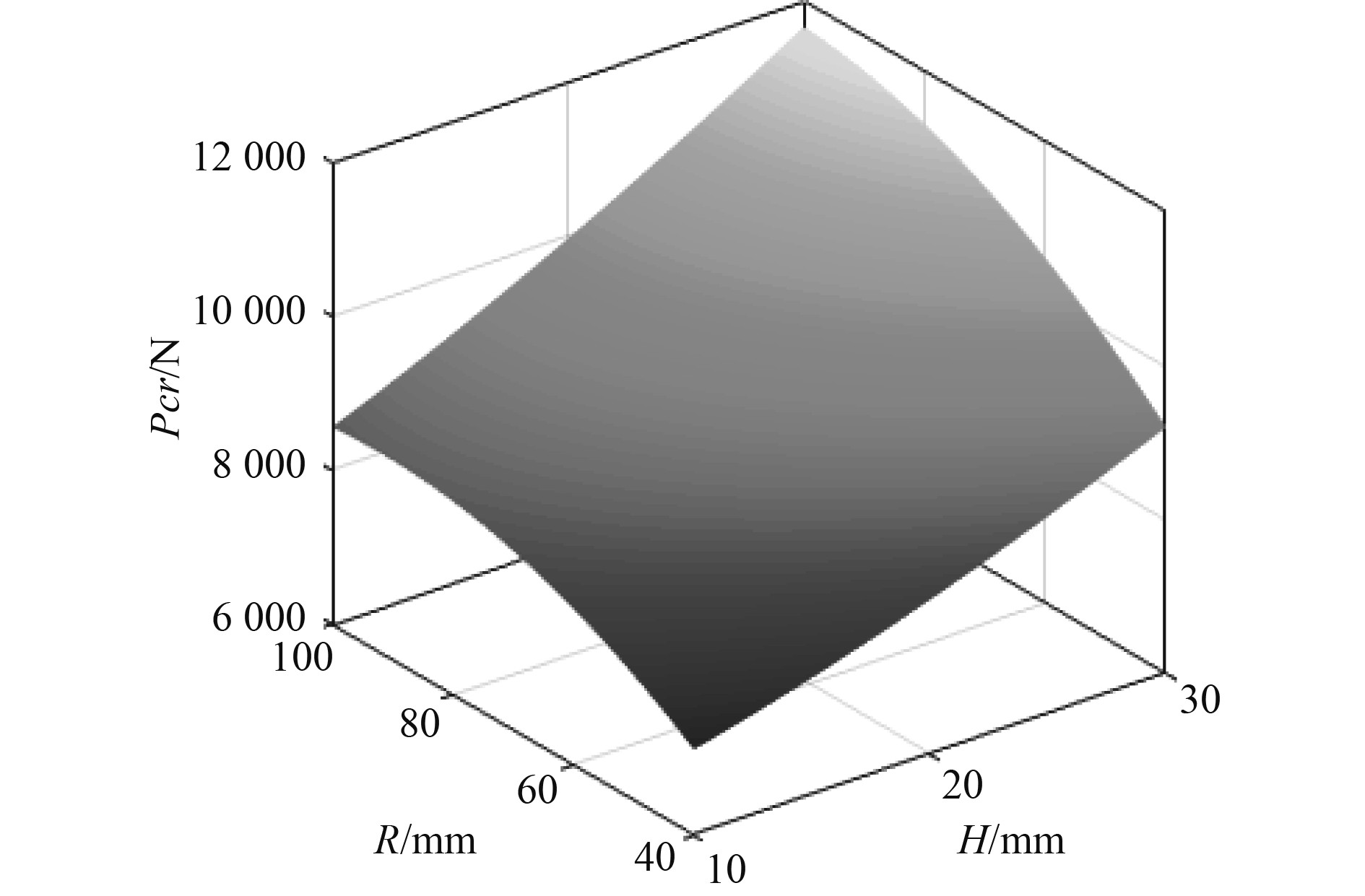
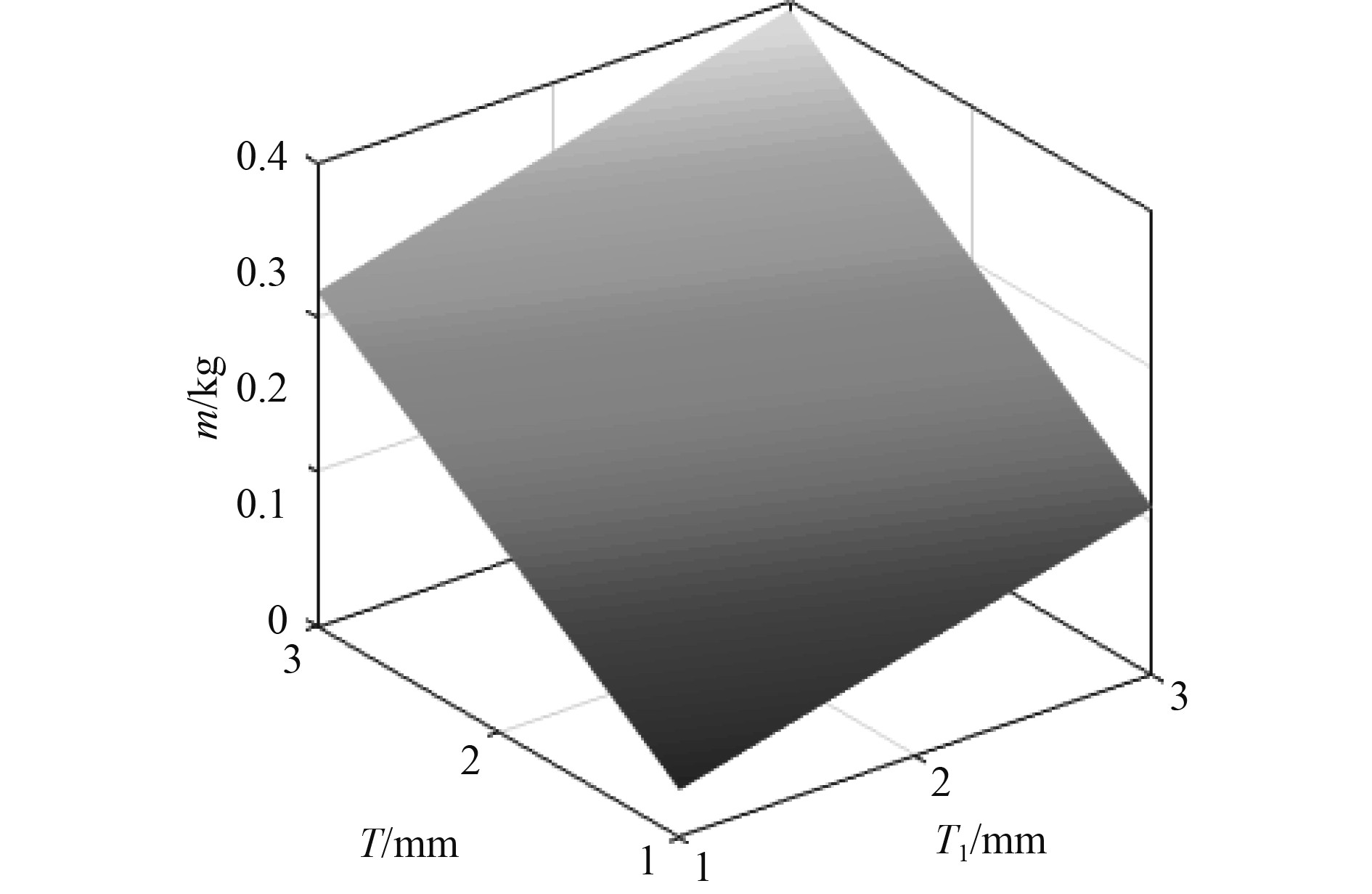
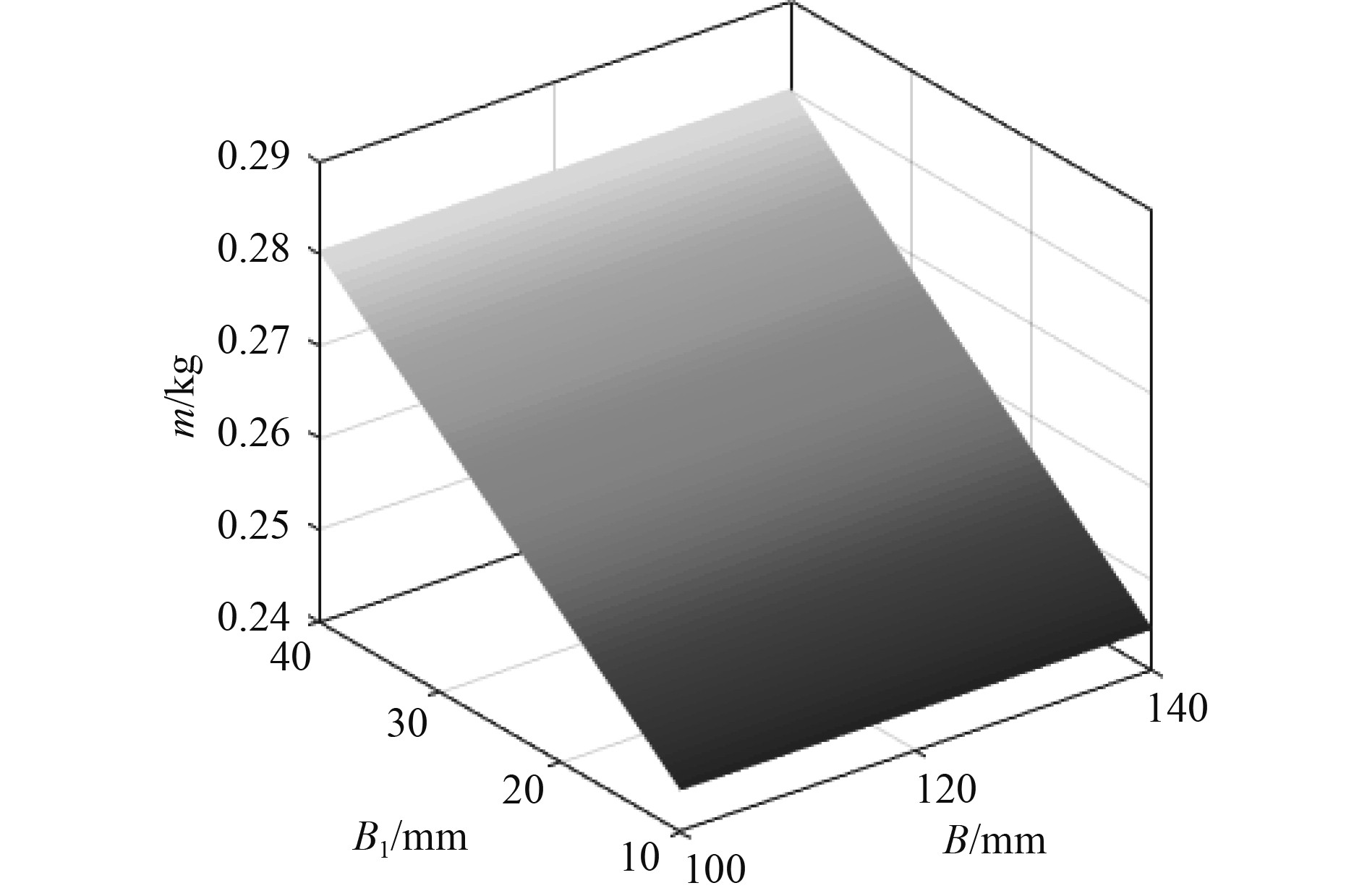
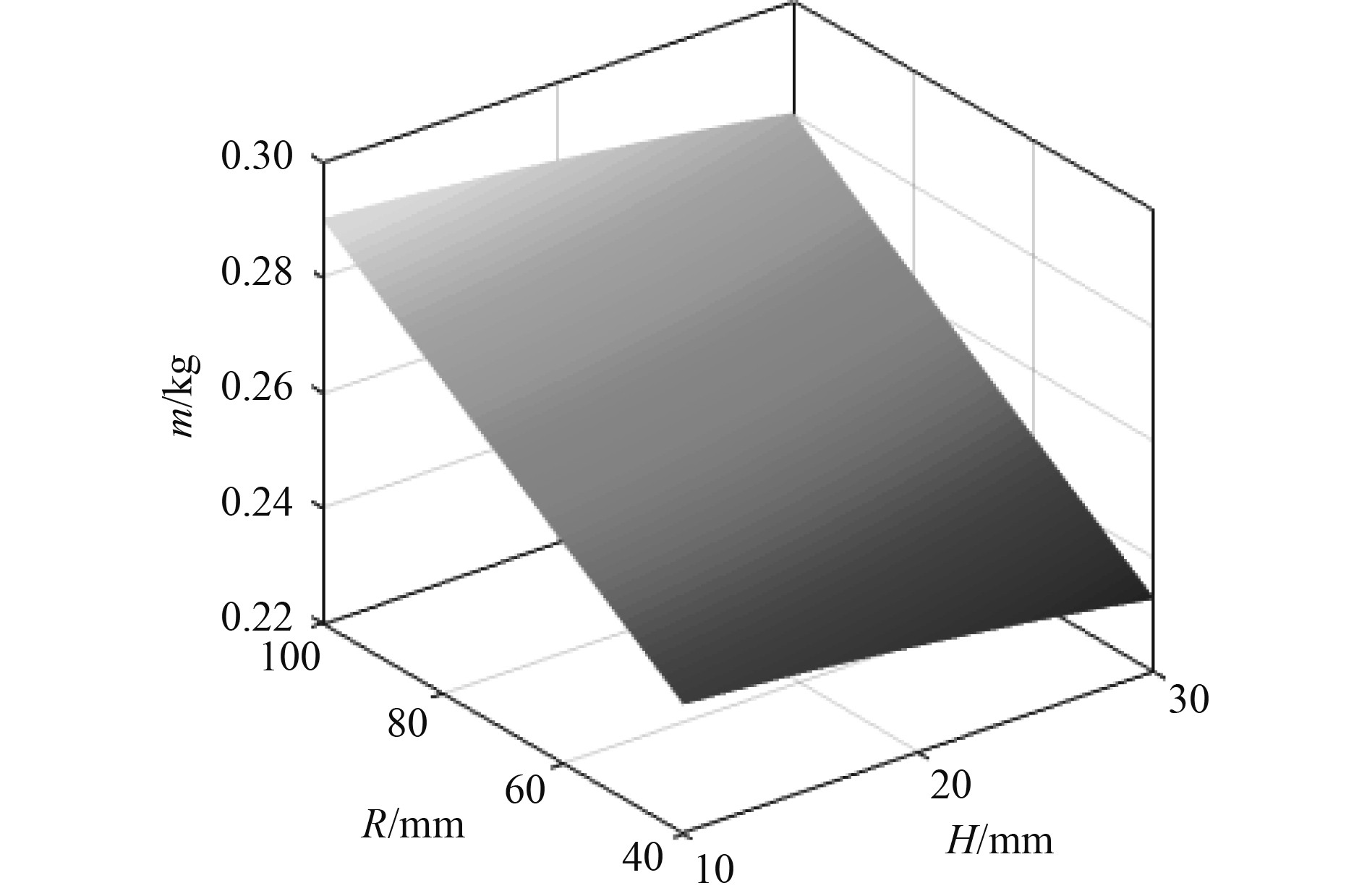
图4~图9为响应面模块中获得的不同设计参数随设计目标变化的3D响应曲面。分析图4~图6发现,开孔板架临界屈曲载荷Pcr随设计变量T、T1、B、R 和H的增加而增大,随参数B1的增加而减小,其中T 对Pcr的影响程度明显大于T1。这与图3灵敏度评估结果一致。由图7~图9可见,板架重量m 随参数T、T1、B1及H 的增加而增大,随参数R 的增加而减小,且m与这些设计变量成线性关系。参数T 对重量的影响最大,参数B变化不影响板架重量。这也与图3局部灵敏度的评估结果一致。
|
图 4 Pcr随T和T1变化响应曲面 Fig. 4 The response surface of Pcr varying with parameters T and T1 |
|
图 5 Pcr随B和B1变化响应曲面 Fig. 5 The response surface of Pcr varying with parameters B and B1 |
|
图 6 Pcr随R和H变化响应曲面 Fig. 6 The response surface of Pcr varying with parameters R and H |
|
图 7 m随T和T1变化响应曲面 Fig. 7 The response surface of m varying with parameters T and T1 |
|
图 8 m随B和B1变化响应曲面 Fig. 8 The response surface of m varying with parameters B and B1 |
|
图 9 m随R和H变化响应曲面 Fig. 9 The response surface of m varying with parameters R and H |
进入响应曲面优化模块,以重量最小和临界屈曲载荷最大为目标,在生成的响应曲面上寻求最优解。根据目标要求,系统自动生成3个候选设计点。参考评价结果,选取重量最低且临界屈曲载荷较大的变量参数作为最终优化结果。表4为复合材料船舶开孔板架的优化设计结果。对比原始设计方案,最佳方案开孔板架的重量减轻了25.9%,抗屈曲能力提升了31.7%,优化效果明显。
|
|
表 4 复合材料开孔板架的优化结果 Tab.4 Optimization results of the composite perforated panel |
基于Workbench 2020 R2仿真计算平台,综合采用DOE试验设计技术、响应面优化模型以及多目标遗传算法,对复合材料船舶开孔板架结构进行了多目标优化设计,获得了重量最小且稳定性较好的最佳设计方案。优化设计方案重量减轻了25.9%,抗屈曲能力提升了31.7%。研究表明,开孔板架的面板厚度、开孔尺寸以及帽型梁的高度、宽度、厚度、梁间距等参数对结构整体的重量和稳定性具有重要影响,设计变量对板架重量和临界屈曲载荷的影响规律分别有T>B1>T1>R>H,T>T1>H>B1>B。
| [1] |
KOLANU N R, RAJU G, RAMJI M. Experimental and numerical studies on the buckling and post-buckling behavior of single blade-stiffened CFRP panels[J]. Composite Structures, 2018, 196. |
| [2] |
李晓文, 朱兆一, 李妍, 等. 复合材料-金属混合船舶极限强度研究综述[J]. 船舶力学, 2020, 24(5): 681-692. LI Xiaowen, ZHU Zhaoyi, LI Yan, et al. A review on ultimate strength of composite-metal hybrid ships[J]. Journal of Ship Mechanics, 2020, 24(5): 681-692. DOI:10.3969/j.issn.1007-7294.2020.05.014 |
| [3] |
李晓文, 邵菲, 朱兆一, 等. 船舶轻量化T型连接结构设计及强度试验[J]. 船舶力学, 2018, 22(4): 454-463. LI Xiaowen, SHAO Fei, ZHU Zhaoyi, et al. Design and strength test of lightweight T joints for ships[J]. Journal of Ship Mechanics, 2018, 22(4): 454-463. DOI:10.3969/j.issn.1007-7294.2018.04.008 |
| [4] |
李晓文, 朱兆一, 李妍, 等. 船舶复合材料加筋板屈曲和后屈曲行为研究[J]. 中国造船, 2020, 61(3): 186-194. LI Xiaowen, ZHU Zhaoyi, LI Yan, et al. Research on buckling and post buckling behavior of composite stiffened panel for ships[J]. Shipbuilding of China, 2020, 61(3): 186-194. DOI:10.3969/j.issn.1000-4882.2020.03.020 |
| [5] |
ZHAO W, XIE Z, WANG X, et al. Buckling behavior of stiffened composite panels with variable thickness skin under compression[J]. Mechanics of Advanced Materials and Structures, 2019, 1-9. |
| [6] |
陈彦廷, 于昌利, 桂洪斌. 船体板和加筋板的屈曲及极限强度研究综述[J]. 中国舰船研究, 2017(1): 54-62. CHEn Yanting, YU Changli, GUI Hongbin. Research development of buckling and ultimate strength of hull plate and stiffened panel[J]. Chinese Journal of Ship Research, 2017(1): 54-62. DOI:10.3969/j.issn.1673-3185.2017.01.009 |
| [7] |
BOX G, WILSON KB. On the experimental attainment of optimum conditions[J]. Journal of the Royal Statistical Society Series B:Statistical Methodology, 1951(1): 1-45. |
| [8] |
隋允康, 宇慧平. 响应面方法的改进及其对工程优化的应用[M]. 北京: 科学出版社, 2011.
|
| [9] |
黄重阳, 林焰, 于雁云. 基于响应面法的强力甲板结构优化设计[J]. 中国舰船研究, 2012, 7(3): 46-50. HUANG Chongyang, LIN Yan, YU Yanyun. Structural optimization of bulk carrier strength deck by response surface methodology[J]. Chinese Journal of Ship Research, 2012, 7(3): 46-50. |
 2022, Vol. 44
2022, Vol. 44
