0 引　言

减摇鳍的基本原理是利用流体与减摇鳍表面相对运动产生的作用力和力矩，抵抗船舶所受到的外界干扰力和力矩，提高船舶的稳定性。由于减摇鳍的体积与流体速度有限，流体流经减摇鳍表面时产生的升力也有一定限制，一旦超出船舶所需的扶正力和力矩，就会破坏船舶的平衡状态，造成船体的倾覆。

主动式减摇鳍针对的船舶工况是零航速状态，此时船舶自身没有前进的速度，固定的减摇鳍无法与流体产生相对运动，因而也不能产生扶正船舶所需的力矩。当船舶处于零航速状态且外界环境相对恶劣时，海风、海浪等干扰因素对船体的载荷会造成船舶横摇角度过大，破坏船体的动态平衡。因此，有必要针对零航速下的船体减摇进行研究。主动式减摇鳍利用机械结构和驱动电机使减摇鳍产生往复运动，产生类似于划桨的力学效果，使零航速时的船舶稳定性提高^[1]。

本文研究的重点在于船舶主动式减摇鳍的流体动力学特性分析，在此基础上设计和开发合理的减摇鳍翼型和形状，并优化减摇鳍在船体的分布定位。

1 船舶横摇运动建模及主动式减摇鳍力学特性分析

在船舶复杂的多自由度运动中，横摇运动对船舶稳定性的影响最大，横摇运动的幅值一旦超限，船舶就会面临进水、沉没的风险。

建立船舶的横摇运动模型为：

$ \left( {{I_x} + \Delta {I_x}} \right)\dfrac{{{{\rm{d}}^2}\alpha }}{{{\rm{d}}{t^2}}} + \dfrac{1}{2}{M_x}\dfrac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} + kh\alpha = f\left( t \right) \text{。} $

式中：h为吃水深度； $ \alpha $ 为船舶的横摇角度变量； $ {I_x} $ 为船舶的转动惯量； $ \Delta {I_x} $ 为附加转动惯量； $ {M_x} $ 为阻尼系数；k为排水量。

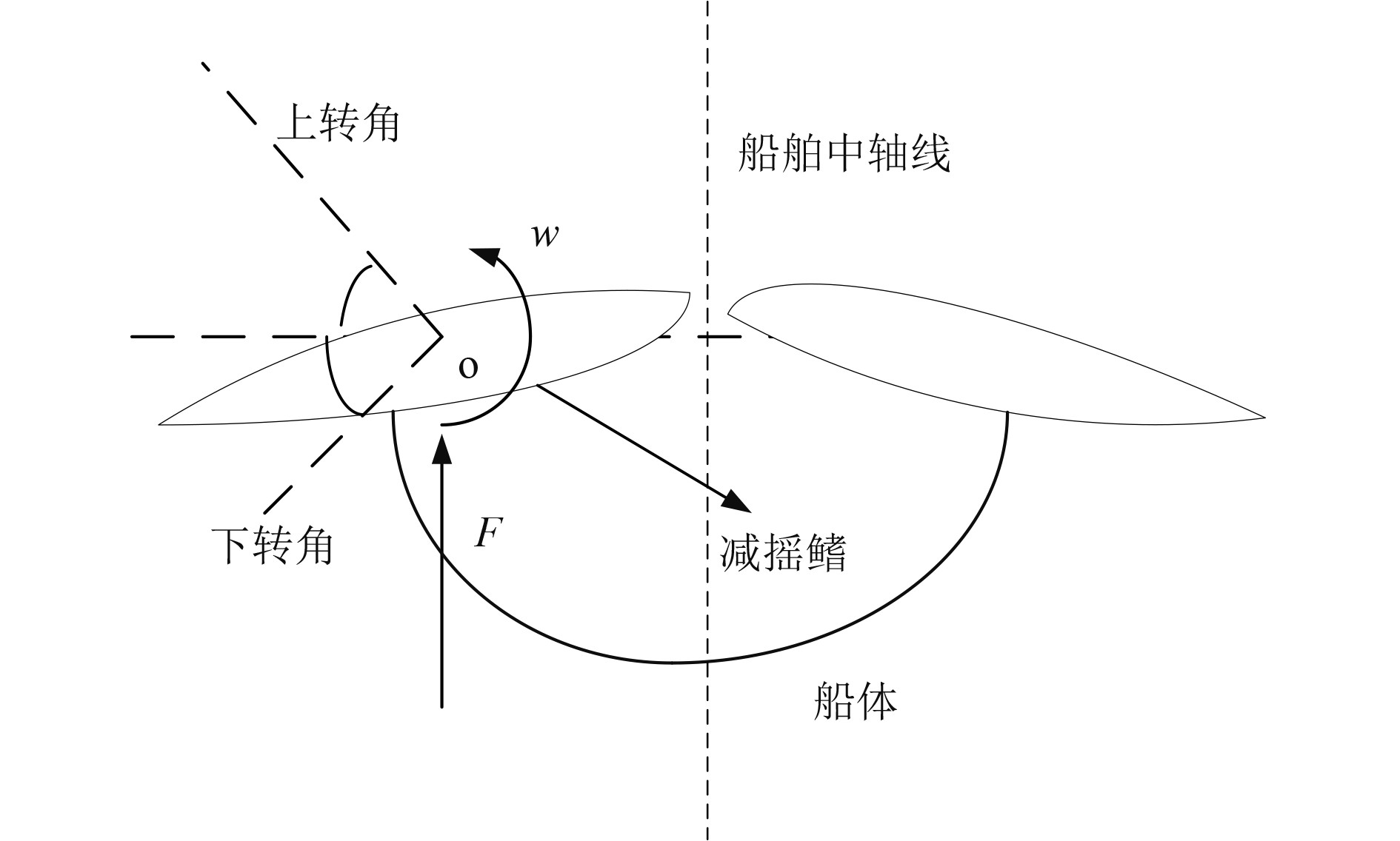
建立船舶主动减摇鳍的数学坐标系如图1所示。

可知，船舶减摇鳍通常对称分布，所受的升力大小相同，方向相反，计算公式如下：

$ {F_S} = \frac{1}{2}{\rho _0}{A_O}{C_0}{v^2} \text{。} $

式中： $ {\rho _0} $ 为流体的密度； $ {A_O} $ 为减摇鳍流速方向的截面投影面积； $ {C_0} $ 为升力系数； $ v $ 为减摇鳍与流体的相对速度。

船舶对称减摇鳍产生的升力由于方向相反，会在船体上产生升力矩，计算公式为：

$ {M_S} = \frac{1}{2}L{\rho _0}{A_O}\cos \theta \text{。} $

式中： $ L $ 为对称减摇鳍之间的距离； $ \theta $ 为减摇鳍转动的角度。

除了升力和升力矩外，船舶主动式减摇鳍还受到波浪弯矩、波浪扭矩、静水弯矩和横摇弯矩等^[2]，分别建模如下：

1）波浪弯矩

波浪弯矩如下式：

$ {M_o} = \frac{1}{2}{k_1}{k_2}L{_b^2}B(\delta + 0.8) \cdot {10^{ - 2}}\;{\rm{kN}} \cdot {\rm{m}} \text{。} $

式中： $ L_b^{} $ 为减摇鳍与水平面切线的长度； $ B $ 为减摇鳍在切线位置的宽度； $ \delta $ 为船舶载重系数； $ \delta \approx 0.5 $ ， $ {k_1} $ 、 $ {k_2} $ 为波浪弯矩系数，计算公式为：

$ {k_1} = 4.5{\left( {\frac{{{L_b}}}{{980}} - 0.2} \right)^2} + 0.82 \text{，} {k_2} = 9 - 0.96{\left( {\frac{{300 - {L_b}}}{{100}}} \right)^2} \text{。} $

2）波浪扭矩

波浪扭矩是指减摇鳍在船舶零航速状态下受波浪作用力产生的扭转特性，计算公式为：

$ {M_n} = {e^{ - 0.00023}}\frac{{{L_b}{B^2}{C_t}}}{{10000}}\left( {1.7 + 1.5\frac{\alpha }{{{h_0}}}} \right) \text{。} $

式中： $ \alpha $ 为减摇鳍在波浪作用载荷下的扭转角度； $ {C_t} $ 为波浪扭矩系数， $ {C_t} = 0.26 $ ； $ {h_0} $ 为船舶减摇鳍重心位置所处的深度。

3）静水弯矩

静水弯矩是船舶减摇鳍受浮力作用产生的弯矩，计算公式为：

$ {M_s} = \iint {\left[ {g(x) - h(x)} \right]}{\rm{d}}x{\rm{d}}x \text{。} $

式中： $ g(x) $ 为减摇鳍的质量分布函数； $ h(x) $ 为减摇鳍浮力变化函数。

4）横摇弯矩

船舶的横摇运动力矩为 $ f\left( t \right) $ ，则减摇鳍受到的最大横摇弯矩为：

$ {T_0} = - f\left( t \right) = 9 \times \frac{{{P_0}(B + {h_0})}}{{600}} \text{。} $

式中： $ {P_0} $ 为船舶的排水量， $ {h_0} $ 为船舶减摇鳍重心位置所处的深度。

2 船舶主动式减摇鳍控制系统设计

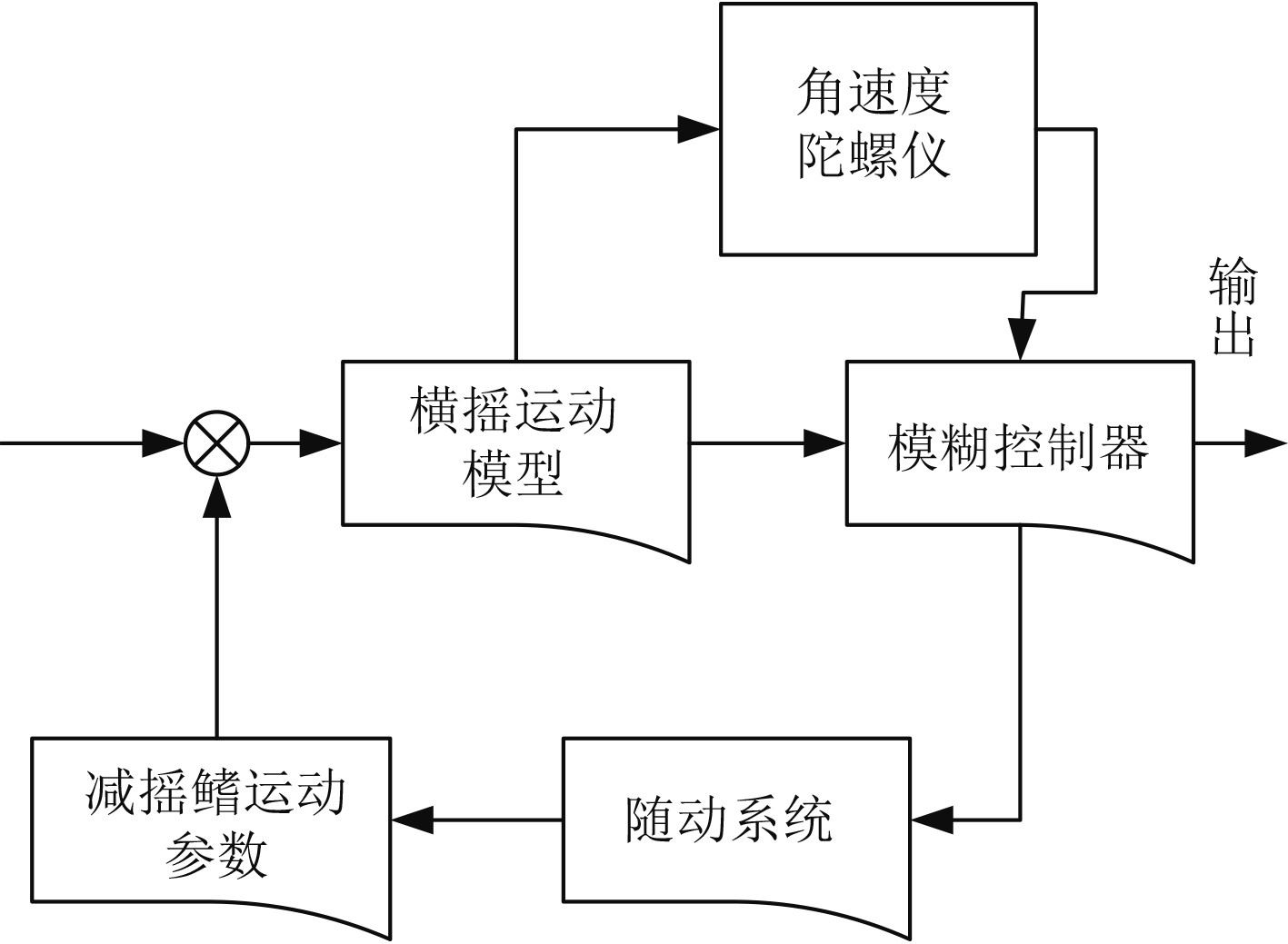
搭建船舶主动式减摇鳍控制系统，基本功能框图如图2所示。

如图，船舶主动式减摇鳍控制系统的控制核心是模糊控制，关键构成包括角速度陀螺仪、模糊控制器、随动系统等。

1）角速度陀螺仪

角速度陀螺仪是控制系统的信号采集模块，采集的关键参数包括减摇鳍的扭转角度、船舶的横摇角度等，通过电压信号传递。

2）模糊控制器

系统采用模糊控制器^[3]作为减摇鳍控制核心，模糊控制系统的权重值集合 $ S = ({b_1},{b_2}...{b_n}) $ ，满足归一性条件如下：

$ \displaystyle\sum\limits_{i = 1}^n {{b_i} = 1} $ 且 $ {b_i} \geqslant 0(i = 1,2,..n) $ 。

3）随动系统

随动系统基于液压驱动原理，为主动式减摇鳍的转动提供力矩，随动系统的传递函数为：

$ {G_t}\left( s \right) = \frac{{550}}{{{s^2} + 15s + 225}} 。$

3 船舶主动式减摇鳍的分布定位和形状设计 3.1 主动式减摇鳍的翼型设计

船舶主动式减摇的翼型设计与减摇鳍的流体动力特性密切相关，减摇鳍的翼型是指鳍最前端点到末端点之间的几何弦线，最前端称为减摇鳍的前缘点，最后端称为减摇鳍的后缘点。翼型上下表面的中点连线称为中弧线，当减摇鳍为对称翼型时^[4]，几何弦线与中弧线重合。通常，为了提高减摇鳍的流体动力学特性，减摇鳍往往不是对称翼型。

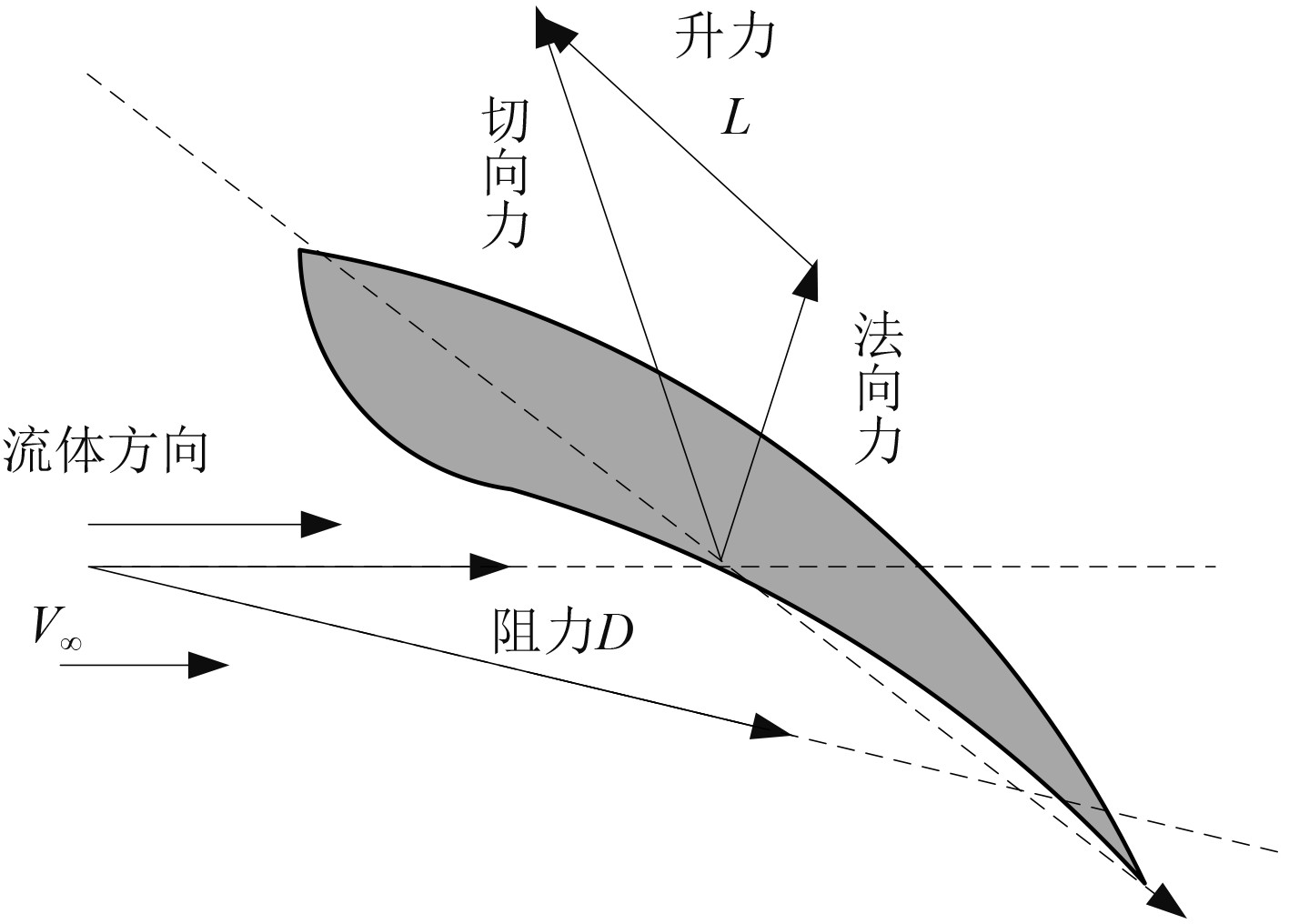
建立减摇鳍的翼型特征曲线示意图如图3所示。

减摇鳍翼型表面的力按照方向可以分为法向力和切向力2种，法向力和切向力的合力为升力，流体运动方向产生阻力。减摇鳍翼型直接影响其升力系数、阻力系数和压强系数，分析计算如下：

1）升力系数

$ {C_L} = \dfrac{L}{{\dfrac{1}{2}\rho V_\infty ^2c}} \text{，} $

式中 $ V_\infty ^{} $ 为流体与减摇鳍的相对运动速度。

2）阻力系数

$ {C_D} = \dfrac{D}{{\dfrac{1}{2}\rho V_\infty ^2c}} 。$

3）压强系数

减摇鳍表面的压力分布也是减摇鳍设计过程需要重点考虑的因素，压强系数计算公式为：

$ {C_p} = \dfrac{{P - {P_\infty }}}{{\dfrac{1}{2}\rho V_\alpha ^2}} \text{。} $

其中： $ P $ 为静水压力； $ {P_\infty } $ 为无穷远处的流体压力。

使用CFD分析软件Fluent^[5]验证了主动式减摇鳍的翼型流体动力学特性，减摇鳍翼型周围流场的压力特性仿真结果如图4所示。

3.2 主动式减摇鳍的形状设计及分布定位

减摇鳍的形状设计是指减摇鳍的表面积尺寸^[6]，不同于减摇鳍的翼型设计，表面积尺寸按下式计算：

$ {L^2} = \frac{{3.5\times {B_0}\times{D_0}}}{{{T^2}\times{V^2}}} \text{。} $

其中： $ {B_0} $ 为减摇鳍的水线面宽； $ {D_0} $ 为减摇鳍排水量； $ T $ 为横摇运动周期； $ V $ 为航行速度。

本文采用的船型 $ {B_0} = 11\;{\rm{m}} $ ， $ {D_0} $ =1080， $ T $ =9， $ V $ =22 km/h，得到形状面积为1.58。

主动式减摇鳍在船体的布置应满足以下条件：

1）横向布置要求

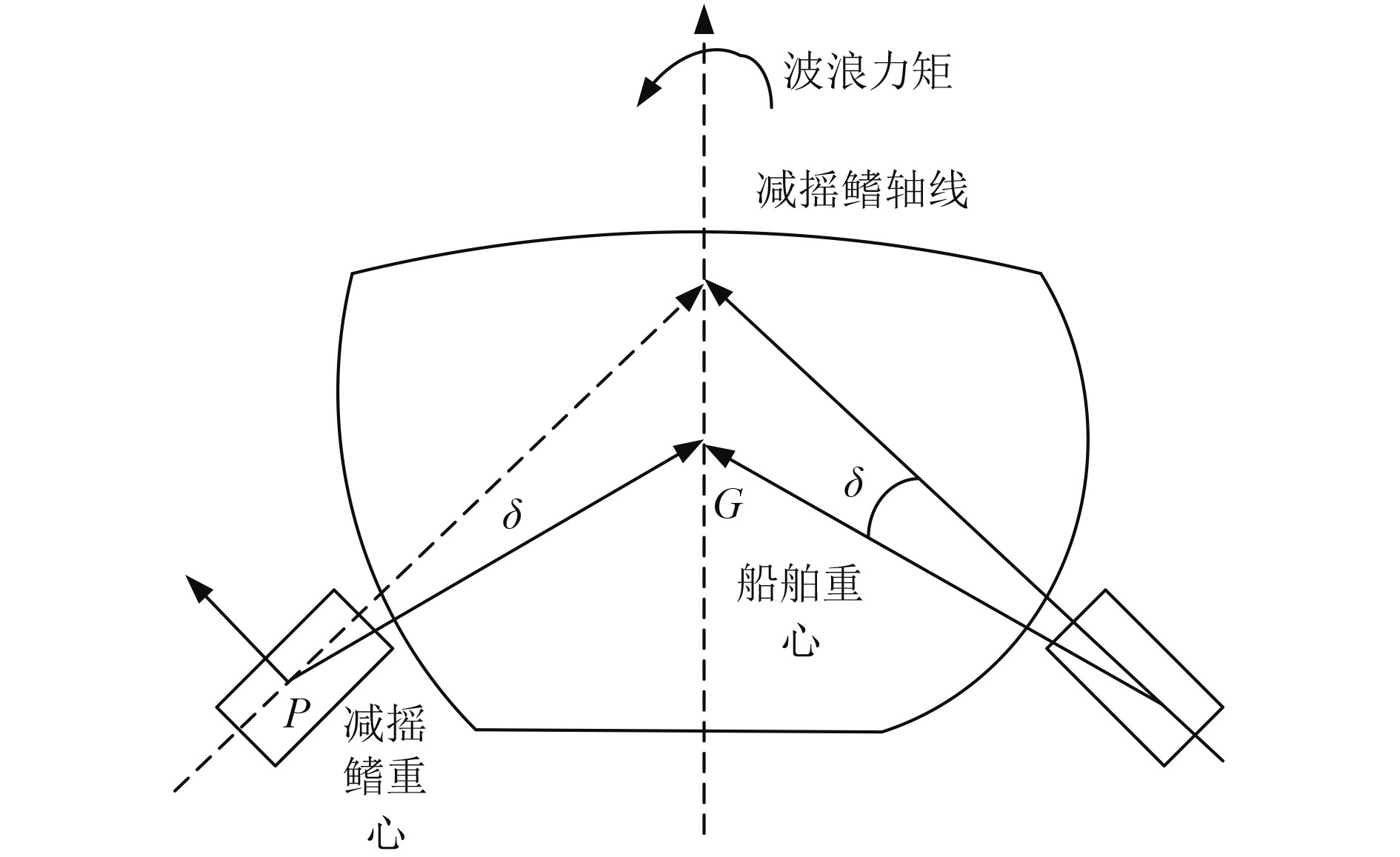
如图5所示，减摇鳍轴线与鳍压力中心、船体重心连线的夹角 $ \delta $ 低于15°。

2）纵向布置要求

若船体纵向布局单个对称减摇鳍，则鳍的位置距离船首或船尾的距离要大于1/3船长，若布置两对减摇鳍，则两鳍之间的距离要小于2/3船长。

3.3 船舶主动式减摇鳍的特性仿真

结合软件平台对船舶主动式减摇鳍的动态特性进行了仿真试验，初始试验参数如表1所示。

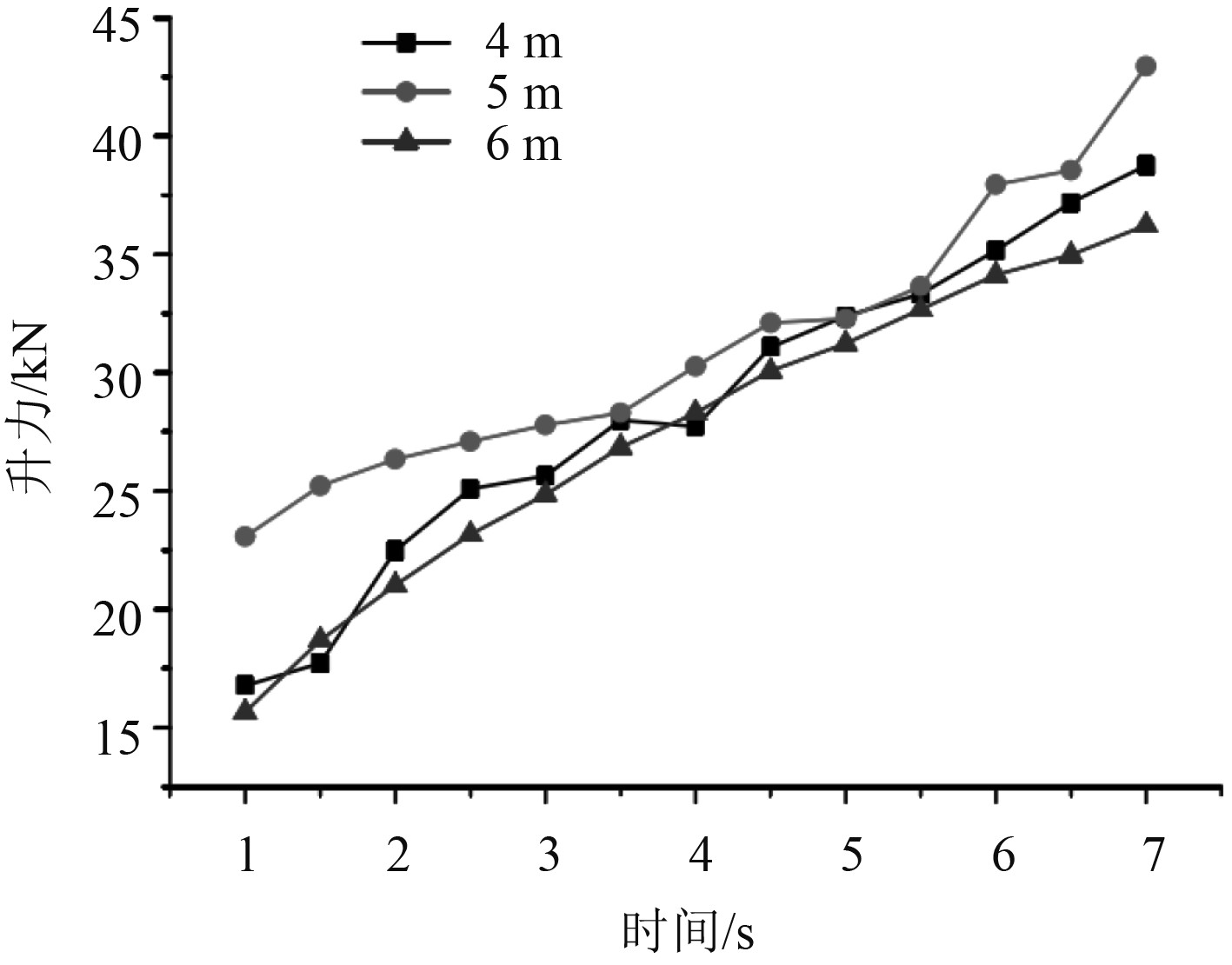
图6为不同波浪高度下的减摇鳍升力特性曲线。

4 结　语

船舶主动式减摇鳍在船舶航行和静止状态下的船舶稳定性控制方面发挥重要作用，本文建立了主动式减摇鳍的力学模型，以此为基础对减摇鳍的翼型、形状及分布特性进行研究，结合CFD软件进行了减摇鳍特性仿真。