舱段分析是船体结构安全性评估中必不可少的内容,由于模型规模小、建模工作量少以及计算成本低等特点,一直都是局部强度、疲劳强度等的主要校核方式之一[1]。同时,为模拟在全船中真实的受力状态,舱段分析需要进行船体梁载荷调整,通过将校核舱段区域的垂向剪力、垂向弯矩、水平弯矩以及扭矩等船体梁载荷调整至规定的值,以准确模拟校核外区域对校核区域的影响[2]。
油船及散货船共同结构规范HCSR(Harmonized Common Structure Rules for Oil Tankers and Bulk Carriers)是国际船级社协会IACS(International Association of Classification Societies)于2013年开始正式推出的目标型标准GBS(Goal-based Standards)下的结构规范[3],对今后相关油船及散货船的结构方面的各项规定做出统一的指导和要求。2020年1月,HCSR2020年1月1日版(以下简称HCSR2020)正式发布,相较于HCSR2019年1月1日版(以下简称HCSR2019)有诸多内容更新,其中针对垂向剪力便提出新的调整要求和相应的方法。
针对HCSR2019和HCSR2020关于垂向剪力调整方法的差异,研究其背后的理论背景,并在此基础上,结合实际校核过程中遇到的问题,提出新的垂向剪力调整方法。
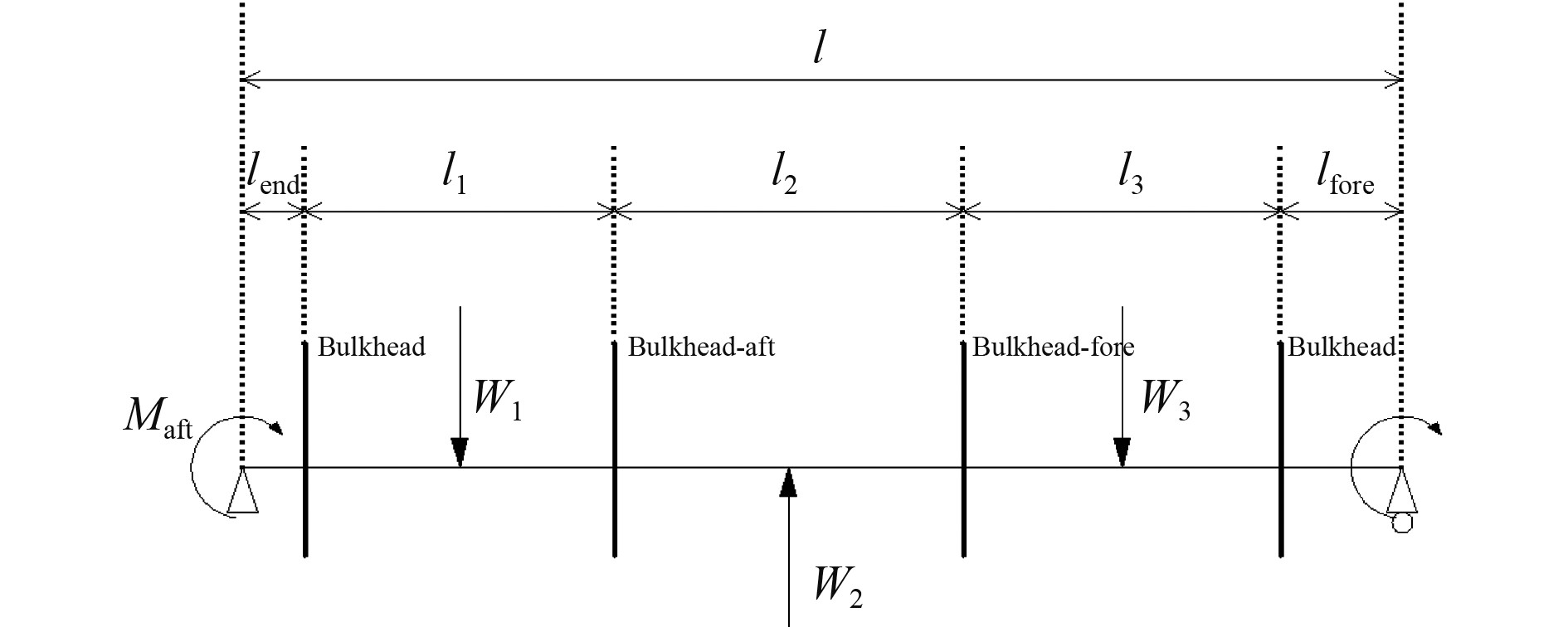
1 HCSR垂向剪力调整方法图1为三舱段模型的简化模型图。图中,l表示三舱段模型的总长度;l1,l2,l3分别表示3舱段模型后舱、中舱、前舱的长度;lfore,lend分别表示模型首尾端面至端部舱壁的距离;Maft,Mfore分别表示施加于模型尾、首端面的剖面弯矩;W1,W2,W3分别表示施加于模型后舱、中舱、前舱中部的垂向集中力;Bulkhead,Bulkhead-aft和Bulkhead-fore表示横舱壁。
|
图 1 垂向剪力调整基本原理图 Fig. 1 Basic principles of vertical shear force adjustment |
垂向剪力调整的目的是通过施加Maft,Mfore,W1,W2,W3等载荷,使得目标位置处(Bulkhead-aft或Bulkhead-fore)的垂向剪力值到达规范规定的目标值。HCSR根据不同工况的需要分为2种方法,分别为Mehtod1和Method2。
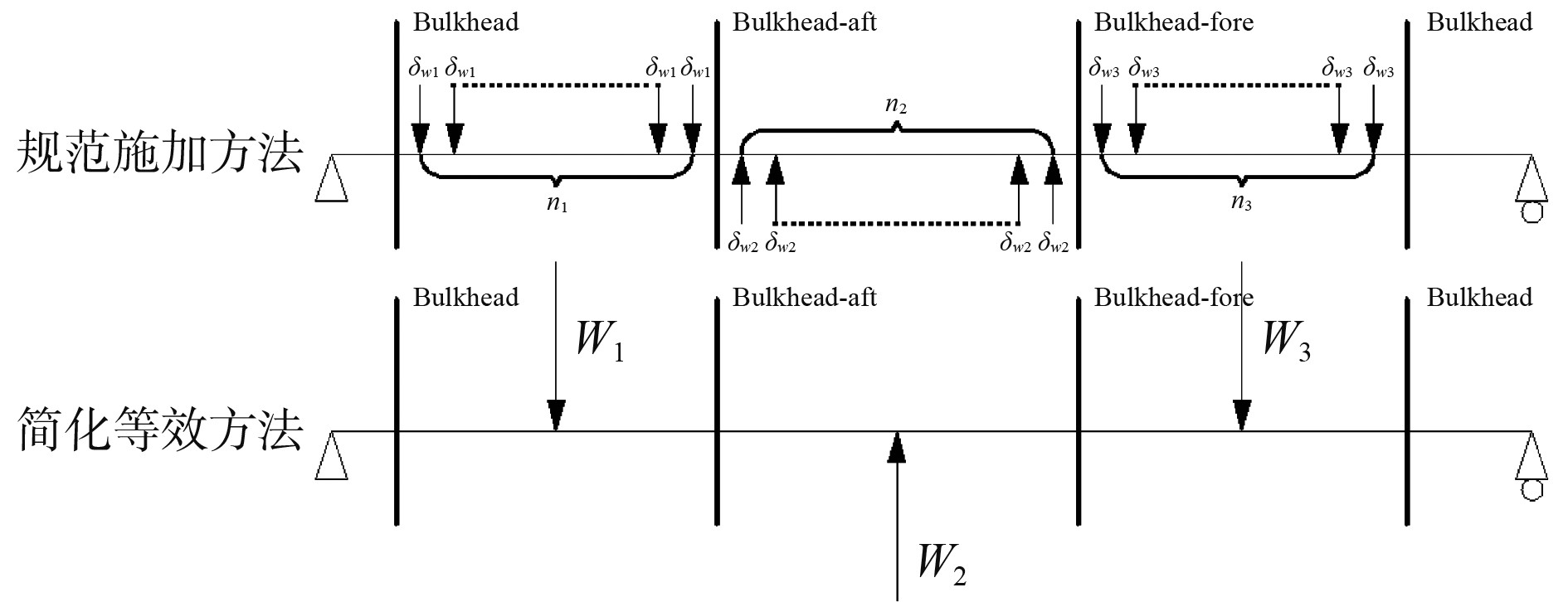
图2为简化分析过程,做了相应的等效转化,把推导的各个公式按δw1=W1/(n1-1),δw2=W2/(n2-1)以及δw3=W3/(n3-1)进行转化,即可得到规范正文的相关公式,其中n1,n2,n3分别表示三舱段模型后舱、中舱、前舱的横向强框架的间距数。
|
图 2 简化等效施加方法示意图 Fig. 2 Sketch of simplified equivalent application method |
方法1:通过施加端部弯矩Maft和Mfore,使某一处(Bulkhead-aft或Bulkhead-fore)的垂向剪力值到达目标值,Maft和Mfore的计算公式为[4]:
| $ {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = {{\Delta Q \cdot l} \mathord{\left/ {\vphantom {{\Delta Q \cdot l} 2}} \right. } 2},$ | (1) |
其中,ΔQ表示目标位置处垂向剪力目标值和由局部载荷引起的垂向剪力值的差值,计算公式:
| $ \Delta Q = \left\{ \begin{gathered} {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}}, \hfill \\ {Q_{{\text{targ - fore}}}} - {Q_{{\text{fwd}}}},\hfill \\ \end{gathered}\right. \begin{array}{l}当调整位置为\text{Bulkhead-aft}时,\\ 当调整位置为\text{Bulkhehead-fore}时。\end{array} $ | (2) |
其中:Qtarg-aft与Qtarg-fwd分别表示Bulkhead-aft和Bulkhead-fore处垂向剪力的目标值;Qaft与Qfwd分别表示Bulkhead-aft和Bulkhead-fore处由局部载荷引起的垂向剪力值。
方法2:通过施加端部弯矩Maft,Mfore以及集中力W1,W2,W3,将Bulkhead-aft和Bulkhead-fore两处位置的垂向剪力值均调整至目标值,计算公式为[4]:
| $\left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = {{\left( {{Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} + {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}}} \right) \cdot l}/4} ,\hfill \\ {W_1} = {\left( {\Delta {Q_{{\text{aft}}}}\left( {2l - {l_2} - {l_3}} \right) + \Delta {Q_{{\text{fwd}}}}\left( {{l_2} + {l_3}} \right)} \right)} /\hfill \\ \qquad\;\; {\left( {2l - {l_1} - 2{l_2} - {l_3}} \right)} ,\hfill \\ {W_2} = \Delta {Q_{{\text{aft}}}} - \Delta {Q_{{\text{fwd}}}},\hfill \\ {W_3} = - {\left( {\Delta {Q_{{\text{fwd}}}}\left( {2l - {l_1} - {l_2}} \right) + \Delta {Q_{{\text{aft}}}}\left( {{l_1} + {l_2}} \right)} \right)} /\hfill \\ \qquad\;\;{\left( {2l - {l_1} - 2{l_2} - {l_3}} \right)} ,\end{gathered} \right. $ | (3) |
其中,
| $\begin{split} \Delta {Q_{{\text{fwd}}}} =& - \Delta {Q_{{\text{aft}}}} ={{\left( {{Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} - \left( {{Q_{{\text{targ - aft}}}} - {Q_{{\text{fwd}}}}} \right)} \right)}/ 2}。\end{split}$ | (4) |
HCSR2020针对除最首最尾区域外的其他区域舱段的垂向剪力调整方法和HCSR2019完全一致,但对于最首和最尾舱段,提出新的调整方法。
方法1:除了在端部施加调整弯矩Maft,Mfore外,还额外在最尾三舱段模型的后舱以及最首三舱段的前舱分别额外的垂向力W′1和W′3,W′1和W′3施加原理同图1及图2中的W1和W3,计算公式为[5]:
| $ 对于最尾三舱段:\left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = {{\Delta Q \cdot l} \mathord{\left/ {\vphantom {{\Delta Q \cdot l} 2}} \right. } 2} - {{M'}_1},\hfill \\ {{W'}_1} = \Delta Q + {R_{{\text{V}}\_{\text{aft}}}}。\hfill \\ \end{gathered} \right. $ | (5) |
| $ 对于最首三舱段:\left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = {{\Delta Q \cdot l} \mathord{\left/ {\vphantom {{\Delta Q \cdot l} 2}} \right. } 2} - {{M'}_3},\hfill \\ {{W'}_3} = \Delta Q + {R_{{\text{V}}\_{\text{fore}}}}。\hfill \\ \end{gathered} \right. $ | (6) |
式中:RV_aft,RV_fore分别表示模型尾、首端面由局部载荷引起的支反力;W’1,W’3分别表示在模型的后、前舱额外施加的垂向集中力;M'1,M'3分别为补充调整扭矩计算公式为:
| $ \left\{ \begin{gathered} {{M'}_1} = (\Delta Q + {R_{{\text{V\_}}aft}}) \cdot {{{l_1}} \mathord{\left/ {\vphantom {{{l_1}} 4}} \right. } 4} ,\hfill \\ {{M'}_3} = (\Delta Q + {R_{{\text{V\_for}}e}}) \cdot {{{l_3}} \mathord{\left/ {\vphantom {{{l_3}} 4}} \right. } 4} 。\hfill \\ \end{gathered} \right. $ | (7) |
方法2:相关参数不变,但计算公式进行改变,各项调整载荷计算公式为[5]:
| $ \left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = ( {Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} +\hfill \\ \qquad\quad {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}} ) \times l / 4 - {{M'}_2} ,\hfill \\ {W_1} = {\left( {\Delta {Q_{{\text{aft}}}}\left( {2l - {l_2} - {l_3}} \right) + \Delta {Q_{{\text{fwd}}}}\left( {{l_2} + {l_3}} \right)} \right)} /\hfill \\ \qquad\;\;{\left( {2l - {l_1} - 2{l_2} - {l_3}} \right)} + {{W'}_1},\hfill \\ {W_2} = \Delta {Q_{{\text{aft}}}} - \Delta {Q_{{\text{fwd}}}},\hfill \\ {W_3} = - {\left( {\Delta {Q_{{\text{fwd}}}}\left( {2l - {l_1} - {l_2}} \right) + \Delta {Q_{{\text{aft}}}}\left( {{l_1} + {l_2}} \right)} \right)} /\hfill \\ \qquad\;\;{\left( {2l - {l_1} - 2{l_2} - {l_3}} \right)} - {{W'}_3} 。\hfill \\ \end{gathered} \right. $ | (8) |
其中,M′2为方法2的补充调整扭矩,其公式为:
| $ 对于最尾舱段:\left\{ \begin{gathered} {{W'}_1} = N + {R_{{\text{V}}\_{\text{aft}}}} ,\hfill \\ {{M'}_2} = {{{{W'}_1} \cdot {l_1}} \mathord{\left/ {\vphantom {{{{W'}_1} \cdot {l_1}} 4}} \right. } 4} ,\hfill \\ {{W'}_3} = 0 。\hfill \\ \end{gathered} \right. $ | (9) |
| $ 对于最首舱段:\left\{ \begin{gathered} {{W'}_3} = N + {R_{{\text{V}}\_{\text{fore}}}} ,\hfill \\ {{M'}_2} = {{{{W'}_3} \cdot {l_3}} \mathord{\left/ {\vphantom {{{{W'}_3} \cdot {l_3}} 4}} \right. } 4} ,\hfill \\ {{W'}_1} = 0。\hfill \\ \end{gathered} \right. $ | (10) |
其中,N为计算系数,其计算公式为:
| $ \begin{split}N =& ( ({Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}})(l - {l_1} - {l_2}) + ({Q_{{\text{targ - fwd}}}} -\\ &{Q_{{\text{fwd}}}})(l - {l_2} - {l_3}) ) / {2l - {l_1} - 2{l_2} - {l_3}}。\end{split}$ | (11) |
HCSR2019中方法1是通过在模型两端施加大小相等的弯矩Maft和Mfore,使整体剪力发生变化,从而达到使需要调整处的剪力到达目标值的目的。根据结构力学,控制方程为:
| $ \left\{ \begin{gathered} {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} = \Delta Q ,\hfill \\ {M_{{\text{aft}}}} = {M_{{\text{fore}}}} 。\hfill \\ \end{gathered} \right. $ | (12) |
求解方程(12),即可获得HCSR2019中方法1的计算公式,即式(1)及式(2)。
HCSR2019中方法2的原理是通过施加集中力W1和W2与W3和端部弯矩Maft和Mfore使Bulkhead-aft和Bulkhead-fore处的剪力值到达目标值。通过分析,其约束条件有:1)首尾弯矩大小相等;2)使Bulkhead-aft处剪力到达目标值;3)使Bulkhead-fore处剪力到达目标值;4)施加的垂向集中力互相力学平衡;5)仅通过施加端部弯矩,使两处目标位置处的剪力和目标值的差值互为相反数。
由此可得其控制方程为:
| $ \left\{ \begin{split} &{M_{{\text{aft}}}} = {M_{{\text{fore}}}},\\ &{{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} / l} + {R_{{\text{va}}}} + {W_1} = {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}} ,\\ &{{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} /l} + {R_{{\text{va}}}} + {W_1}{{ - }}{W_2} = {Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} ,\\ & {W_1} + {W_3} = {W_2} ,\\ &{Q_{{\text{targ - aft}}}} - \left( {{Q_{{\text{aft}}}} + {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)}/ l}} \right) = \\ & \qquad- \left( {{Q_{{\text{targ - fwd}}}} - \left( {{Q_{{\text{fwd}}}} + {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} / l}} \right)} \right) 。\end{split} \right. $ | (13) |
其中,Rva为由W1和W2与W3引起的尾端面支反力,根据结构力学[6],公式为:
| $\begin{split} {R_{{\text{va}}}} =& \left( {{{W_1} \cdot \left( { - 2l + {l_1} + 2{l_{{\text{end}}}}} \right)} / {2l}} + {{W_2} \cdot \left( {2l - 2{l_1} - {l_2} - 2{l_{{\text{end}}}}} \right)} / \right.\\ & \left. {2l} + {{{W_3} \cdot \left( { - 2l + 2{l_1} + 2{l_2} + {l_3} + 2{l_{{\text{end}}}}} \right)} / {2l}} \right)。\\[-10pt] \end{split}$ | (14) |
求解方程(13),即可获得HCSR2019中方法2的计算公式,即式(3)及式(4)。
2.2 HCSR2020垂向剪力调整方法原理以最尾三舱段模型为例,方法1通过施加Maft、Mfore以及W′1,使得除目标位置的垂向剪力值到达目标值外,额外使得模型尾端面的支反力为0。
由此可得其约束条件为:1)前后的调整施加弯矩相等;2)模型尾端面支反力为0;3)目标位置的垂向剪力值到达目标值,即目标位置剪力变化ΔQ。因此,控制方程为:
| $ \left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}},\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {R_{{\text{vb}}}} + {R_{{\text{V}}\_{\text{aft}}}} = 0,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {R_{{\text{vb}}}} + {{W'}_1} = \Delta Q。\hfill \\ \end{gathered} \right. $ | (15) |
其中,Rvb为由W'1引起的尾端面支反力,根据结构力学[6],计算公式为:
| $ {R_{{\text{vb}}}} = {{{{W'}_1} \cdot ({l_1} + 2{l_{{\text{end}}}})} \mathord{\left/ {\vphantom {{{{W'}_1} \cdot ({l_1} + 2{l_{{\text{end}}}})} {2l}}} \right. } {2l}} - {W'_1} 。$ | (16) |
对于最尾三舱段模型,lend=0,将其代入式(15)并求解,即可获得HCSR2020中方法1针对最尾三舱段模型的垂向剪力调整公式,即式(5)~式(7)。
方法2通过施加Maft,Mfore以及W1,W2,W3,除使得Bulkhead-aft和Bulkhead-fore处的垂向剪力值到达目标值外,还额外使得模型尾端面的支反力为0。
根据分析,HCSR2020中方法2的约束条件为:1)首尾弯矩大小相等;2)使Bulkhead-aft处剪力到达目标值;3)使Bulkhead-fore处剪力到达目标值;4)调整完后尾端面最终的垂向剪力为0;5)调整完后首端面最终的垂向剪力同原HCSR方法调整完后相同,即W3不变。
由此可得新的控制方程为:
| $ \left\{ \begin{split} {M_{{\text{aft}}}} = {M_{{\text{fore}}}},\hfill \\ &{{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {R_{{\text{va}}}} + {W_1} = {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}} ,\hfill \\ &{{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} / l} + {R_{{\text{va}}}} + {W_1} - {W_2} = {Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} ,\hfill \\ &{{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {R_{{\text{va}}}} + {R_{{\text{V}}\_{\text{aft}}}} = 0 ,\hfill \\ &{W_3} = - \left( {{Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} - \left( {{Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}}} \right)} \right) \times \hfill\\ &\qquad\;\; \left( {l - {l_1} - {l_2}} \right) /{\left( {2l - {l_1} - 2{l_2} - {l_3}} \right)}。\end{split} \right. $ | (17) |
求解方程(17),即可获得HCSR2020中方法2针对最尾三舱段模型的垂向剪力调整公式,即式(8)~式(11)。
同理,将上述约束条件中的“模型尾端面支反力为0”改为“模型首端面支反力为0”,可得HCSR2020中针对最首三舱段的垂向剪力调整公式。
3 垂向剪力调整新方法研究HCSR2020相对于HCSR2019,对于最首和最尾区域舱段,除了使得目标区域的垂向剪力值到达目标值外,还额外要求最尾舱段的尾端面和最首舱段的首端面的支反力为0,原因是防止端面过大的支反力会影响目标位置的剪力校核结果[7]。
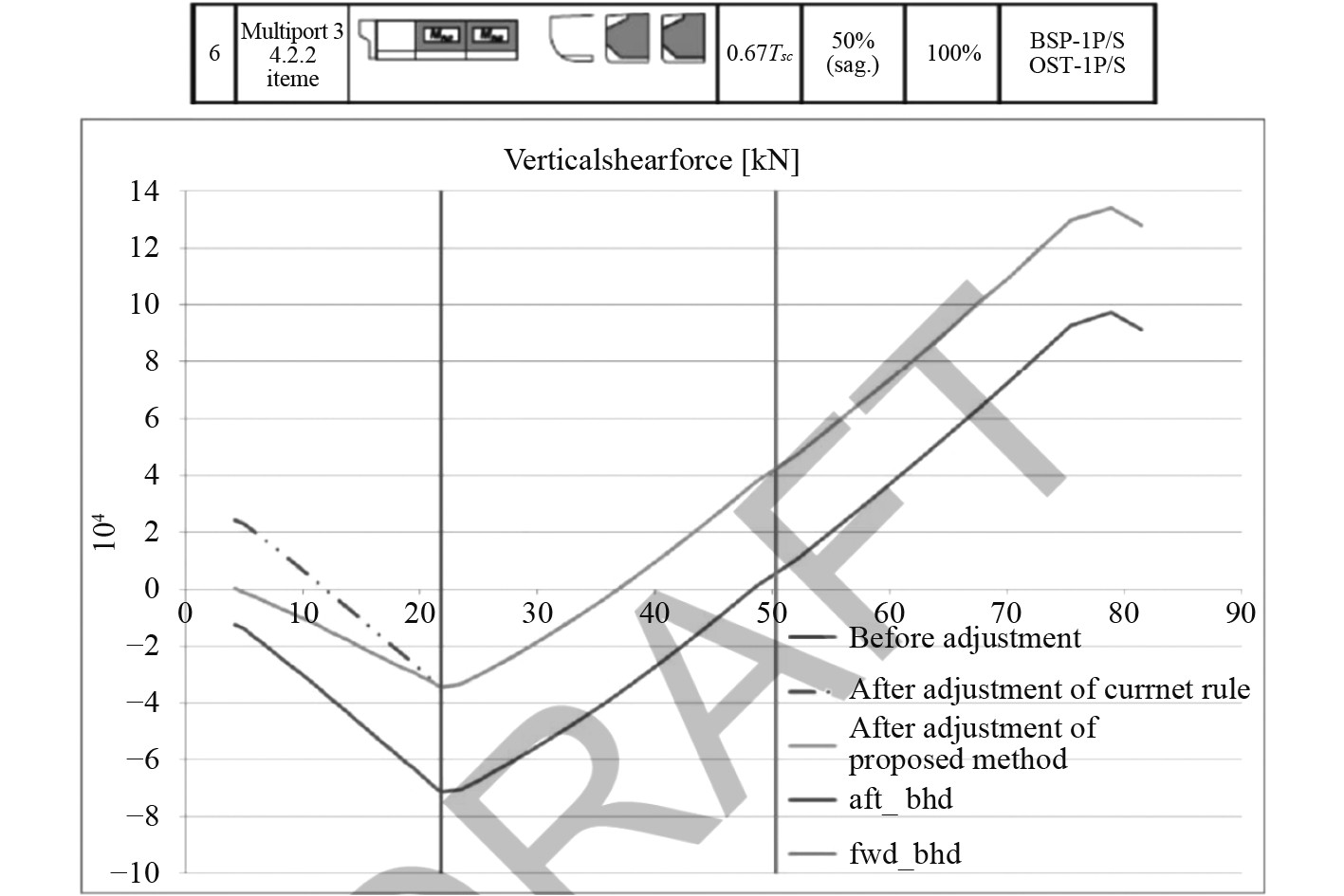
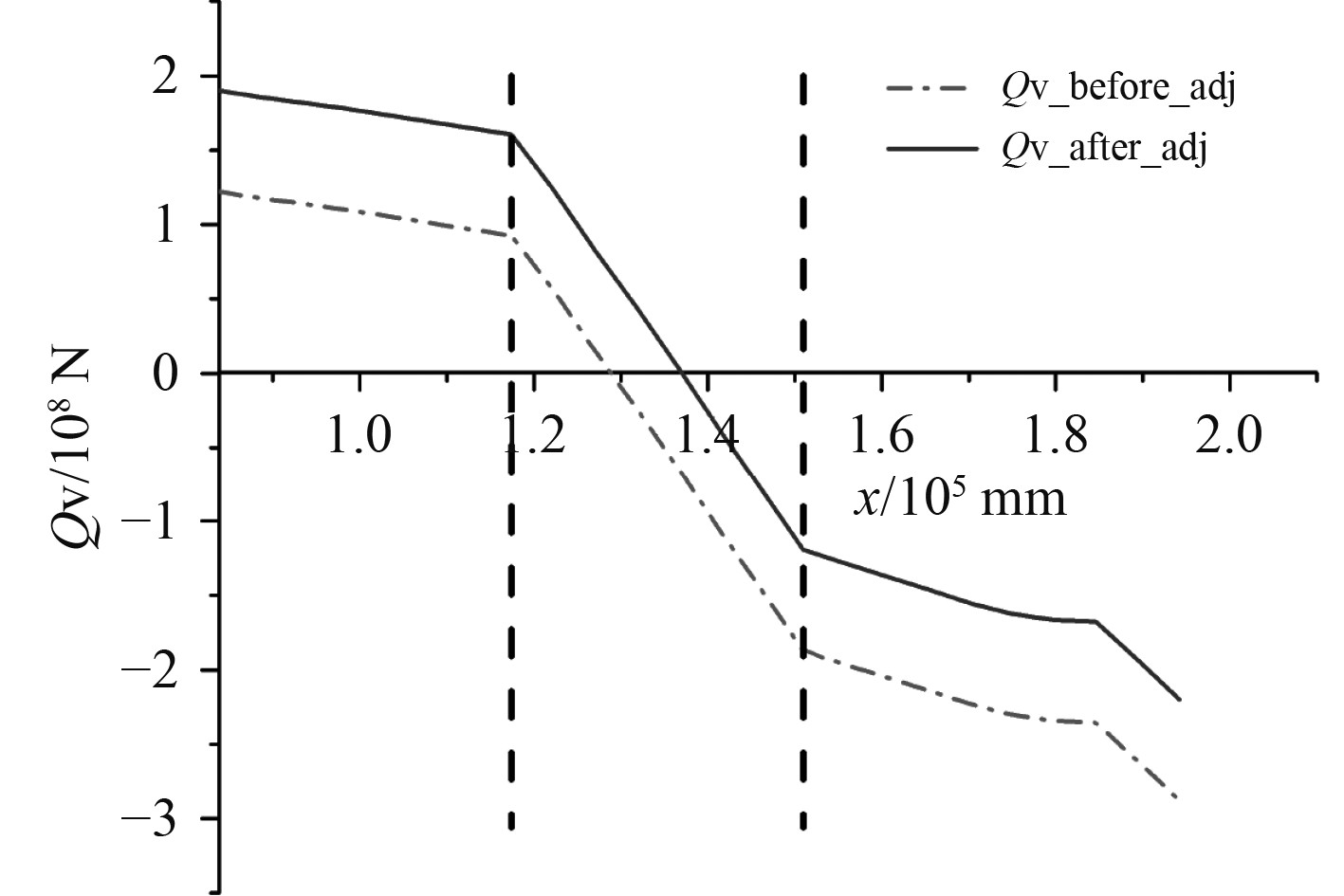
但在实际的舱段校核中发现,针对垂向剪力值的调整依然存在问题。图3为某散货船最尾三舱段的垂向剪力调整结果,其中Before Adjustment,After Adjustment of Current Rules,After Adjustment of Proposed Method分别表示未调整、HCSR2019方法、HCSR2020方法调整后的垂向剪力分布,Aft_bhd和fore_bhd分别表示Bulkhead-aft和Bulkhead-fore的位置;图4为某158 K油船船中三舱段垂向剪力调整结果,其中Qv_before_adj和Qv_after_adj分别表示由HCSR方法(HCSR2019和HCSR2020针对船中舱段的调整方法完全相同)调整前和调整后的垂向剪力分布。
|
图 3 某散货船最艉舱段垂向剪力调整结果[7] Fig. 3 Vertical shear force adjustment results for aft most cargo holds of a bulk carrier |
|
图 4 某158 K油船船舯舱段垂向剪力调整结果 Fig. 4 Vertical shear force adjustment results for mid cargo holds of an 158 K oil tanker |
可知,垂向剪力调整还存在以下问题:
1)对于最首最尾舱段,除规范(HCSR2020)要求的端面外,另一处端面的支反力依然存在过大的情况,依然可能会对校核结果产生影响;
2)对于非最首最尾舱段,也存在端面处支反力过大从而影响剪力校核结果的问题。
最理想的情况,是针对任意区域舱段,除使目标位置的垂向剪力值到达目标值外,还应额外使得首尾2个端面的支反力都为0。因此,结合HCSR2020的相关思路,对垂向剪力调整方法进行进一步修正,使得新方法能除了将所需位置的垂向剪力调整到目标值外,还使得模型(任意区域)首尾端面的支反力均为0,具体方法如下:
方法1:除端部弯矩Maft和Mfore外,添加2个垂向力W′1和W′3,满足以下约束条件:1)前后的调整施加弯矩相等;2)目标位置(Bulkhead-aft或Bulkhead-fore)的垂向剪力值到达目标值;3)模型尾端面支反力为0;4)模型首端面支反力为0。
由此可得其控制方程如下:
| $ \left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}},\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {{R'}_{{\text{vb}}}} + {R_{{\text{V}}\_{\text{aft}}}} = 0,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {{R'}_{{\text{vb}}}} + {{W'}_1} = \Delta Q ,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} l}} \right. } l} + {{R'}_{{\text{vb}}}} + {{W'}_1} + {{W'}_3} + {R_{{\text{V}}\_{\text{fore}}}} = 0。\hfill \\ \end{gathered} \right. $ | (18) |
其中,R′vb为由W′1和W′3引起的尾端面支反力,根据结构力学[6],可由下式计算:
| $ \begin{split}{R'_{{\text{vb}}}} =& {W'_1} \cdot {{\left( { - 2l + {l_1} + 2{l_{{\text{end}}}}} \right)} / {2l}} + {W'_3} \times\\ &{{\left( { - 2l + 2{l_1} + 2{l_2} + {l_3} + 2{l_{{\text{end}}}}} \right)} / {2l}}。\end{split}$ | (19) |
求解方程(18)可得:
| $ \left\{ \begin{gathered} {{W'}_1} = \Delta Q + {R_{{\text{V\_aft}}}} ,\hfill \\ {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = \hfill \\ \qquad\quad \left( \begin{gathered} {{\Delta Q \cdot \left( {{l_1} + 2{l_2} + {l_3}} \right)} /4} - {{{R_{{\text{V\_aft}}}} \times \left( {{l_1} + 2{l_{{\text{end}}}}} \right)} /4} \hfill \\ - {{{R_{{\text{V}}\_{\text{fore}}}} \cdot \left( {2l - 2{l_1} - 2{l_2} - {l_3} - 2{l_{{\text{end}}}}} \right)} / 4} \hfill \\ \end{gathered} \right),\hfill \\ {{W'}_3} = - {R_{{\text{V}}\_{\text{fore}}}} - \Delta Q 。\hfill\\ \end{gathered} \right. $ | (20) |
方法2:Maft,Mfore,W1,W2,W3的约束条件变为:1)首尾弯矩大小相等;2)使Bulkhead-aft处剪力到达目标值;3)使Bulkhead-fore处剪力到达目标值;4)调整完后尾端面支反力为0;5)调整完后首端面支反力为0。
由此可得其控制方程为:
| $ \left\{ \begin{gathered} {M_{{\text{aft}}}} = {M_{{\text{fore}}}} ,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} /l} + {R_{{\text{va}}}} + {W_1} = {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}} ,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} / l} + {R_{{\text{va}}}} + {W_1}{\text{ - }}{W_2}= {Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}} ,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} /l} + {R_{{\text{va}}}} + {R_{{\text{V}}\_{\text{aft}}}} = 0 ,\hfill \\ {{\left( {{M_{{\text{aft}}}} + {M_{{\text{fore}}}}} \right)} /l} + {R_{{\text{va}}}} + {W_1}{{ - }}{W_2} + {W_3} + {R_{{\text{V}}\_{\text{fore}}}} = 0 。\end{gathered} \right. $ | (21) |
求解方程(21)可得:
| $ \left\{ \begin{gathered} {W_1} = {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}} + {R_{{\text{V}}\_{\text{aft}}}} ,\hfill \\ {W_2} = {Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}} - ({Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}}),\hfill \\ {W_3} = - {R_{{\text{V}}\_{\text{fore}}}} - ({Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}}) ,\hfill \\ {M_{{\text{aft}}}} = {M_{{\text{fore}}}} = \left( \begin{gathered} {{({Q_{{\text{targ - aft}}}} - {Q_{{\text{aft}}}}) \times \left( {{l_1} + {l_2}} \right)} / 4} + \hfill \\ {{({Q_{{\text{targ - fwd}}}} - {Q_{{\text{fwd}}}}) \times \left( {{l_2} + {l_3}} \right)} / 4} \hfill \\ - {{{R_{{\text{V}}\_{\text{aft}}}} \cdot \left( {{l_1} + 2{l_{{\text{end}}}}} \right)} / 4} - {R_{{\text{V}}\_{\text{fore}}}} \times \hfill \\ \left( {2l - 2{l_1} - 2{l_2} - {l_3} - 2{l_{{\text{end}}}}} \right)/ 4 \hfill \\ \end{gathered} \right) 。\end{gathered} \right. $ | (22) |
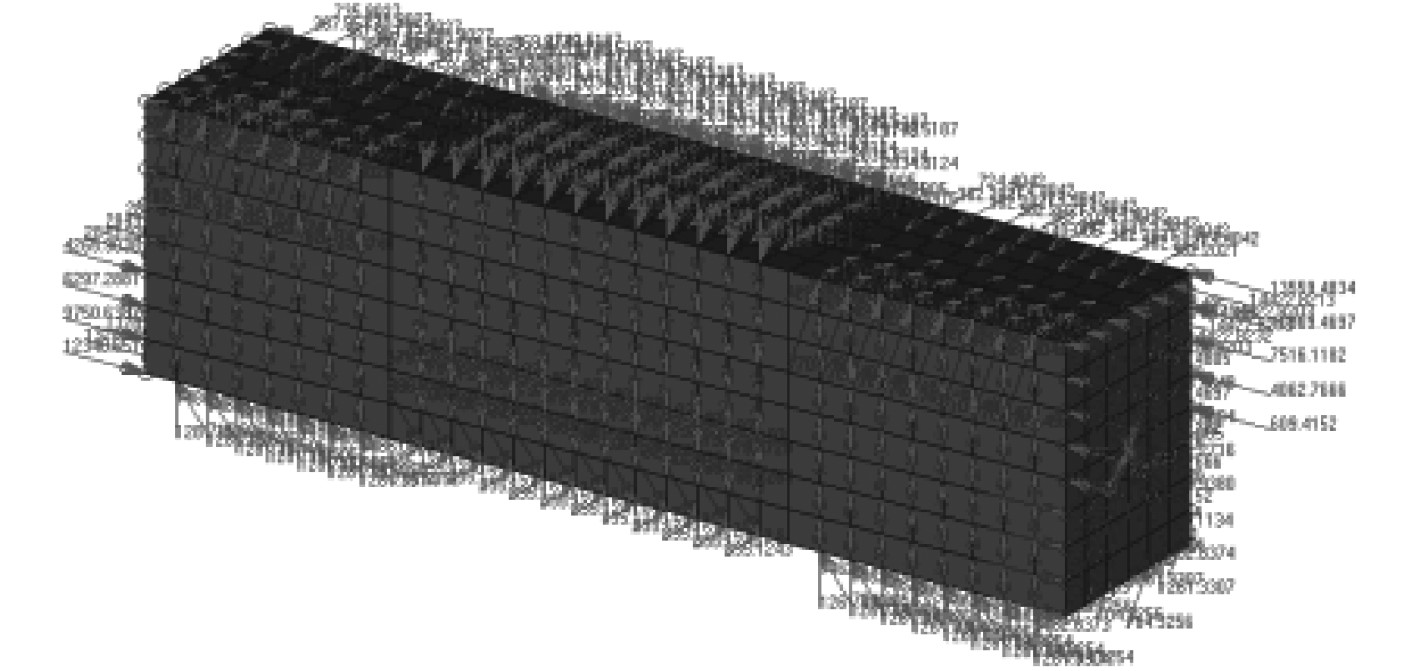
采用简化模型对上述相关公式进行数值验证,本次简化模型模拟的是最尾三舱段,对模型施加局部载荷,并分别采用HCSR2019,HCSR2020以及本文的新方法对其垂向剪力进行调整,然后根据应力计算结果,积分获得各个剖面的垂向剪力值[8]。模型局部载荷以及调整载荷施加效果如图5和图6所示。

|
图 5 理想模型及局部载荷加载示意图 Fig. 5 Idea model and the application of local loads |
|
图 6 调整载荷加载示意图 Fig. 6 Application of adjustment loads |
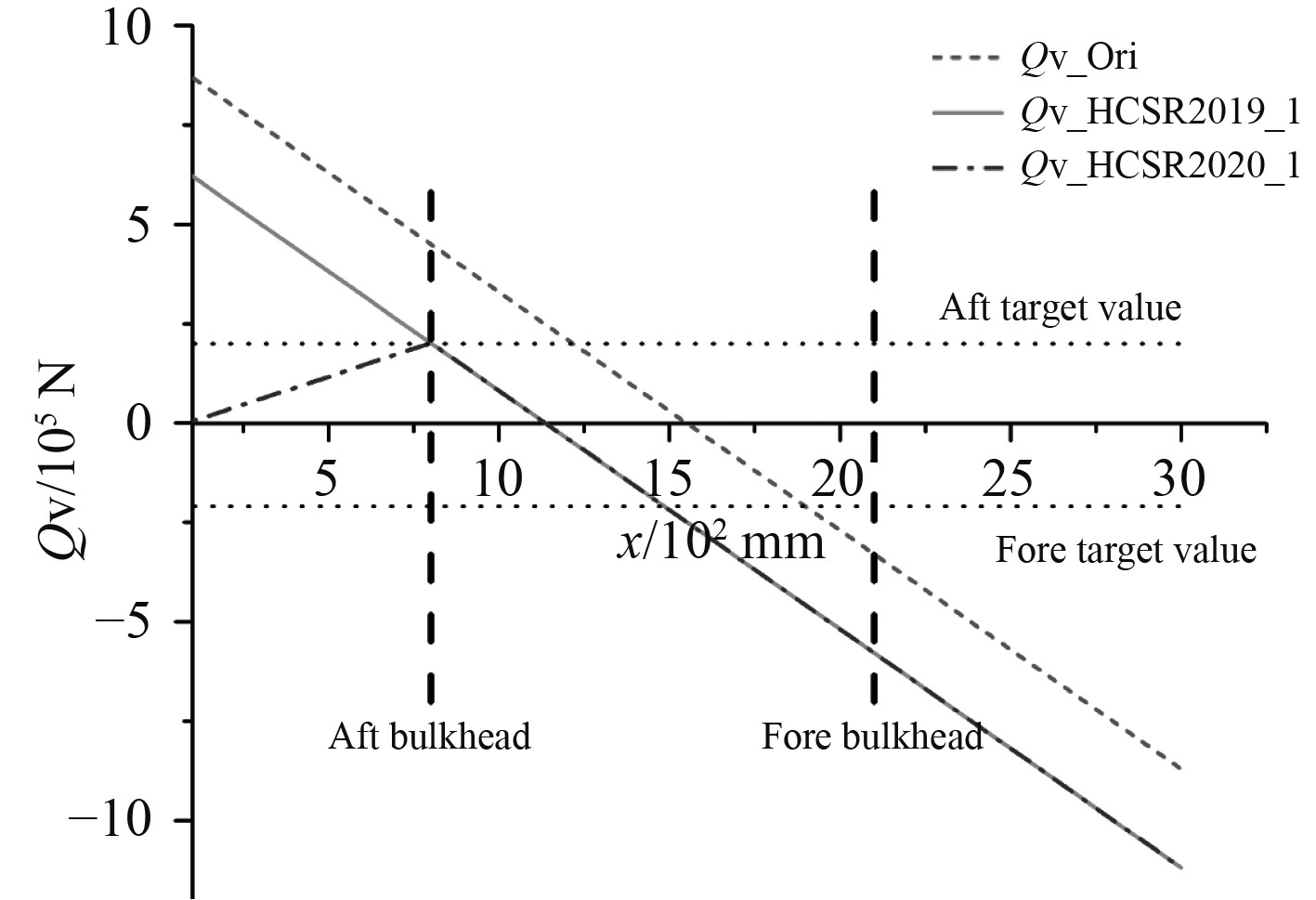
调整后的计算结果如图7~图10所示。其中Aft Bulkhead,Fore Bulkhead,Aft Target Value以及Fore Target Value分别表示三舱段模型中间评估舱段的后舱壁和前舱壁的位置及该位置处的垂向剪力目标值,Qv_Qri表示仅由局部载荷引起垂向剪力,Qv_HCSR2019_1,Qv_HCSR2019_2,Qv_HCSR2020_1,Qv_HCSR2020_2,Qv_NEW_1以及Qv_NEW_2分别表示HCSR2019和HCSR2020以及本文新方法中的方法1和方法2的调整结果。
|
图 7 HCSR2019和HCSR2020的方法1对比结果 Fig. 7 Comparison results between HCSR2019 and HCSR2020 in method1 |
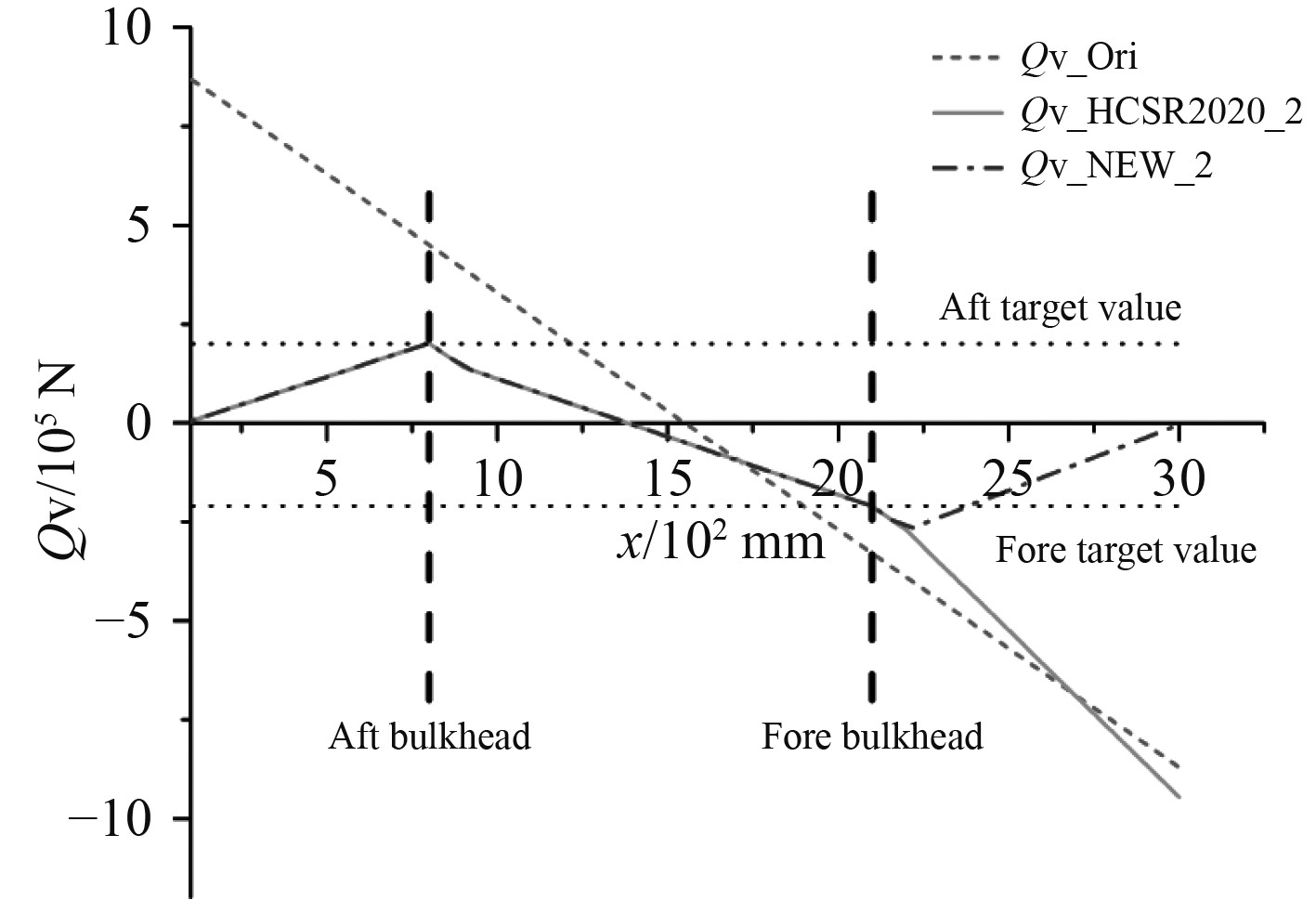
|
图 10 HCSR2020和本文新方法的方法2对比结果 Fig. 10 Comparison results between HCSR2020 and new method of the article in method2 |
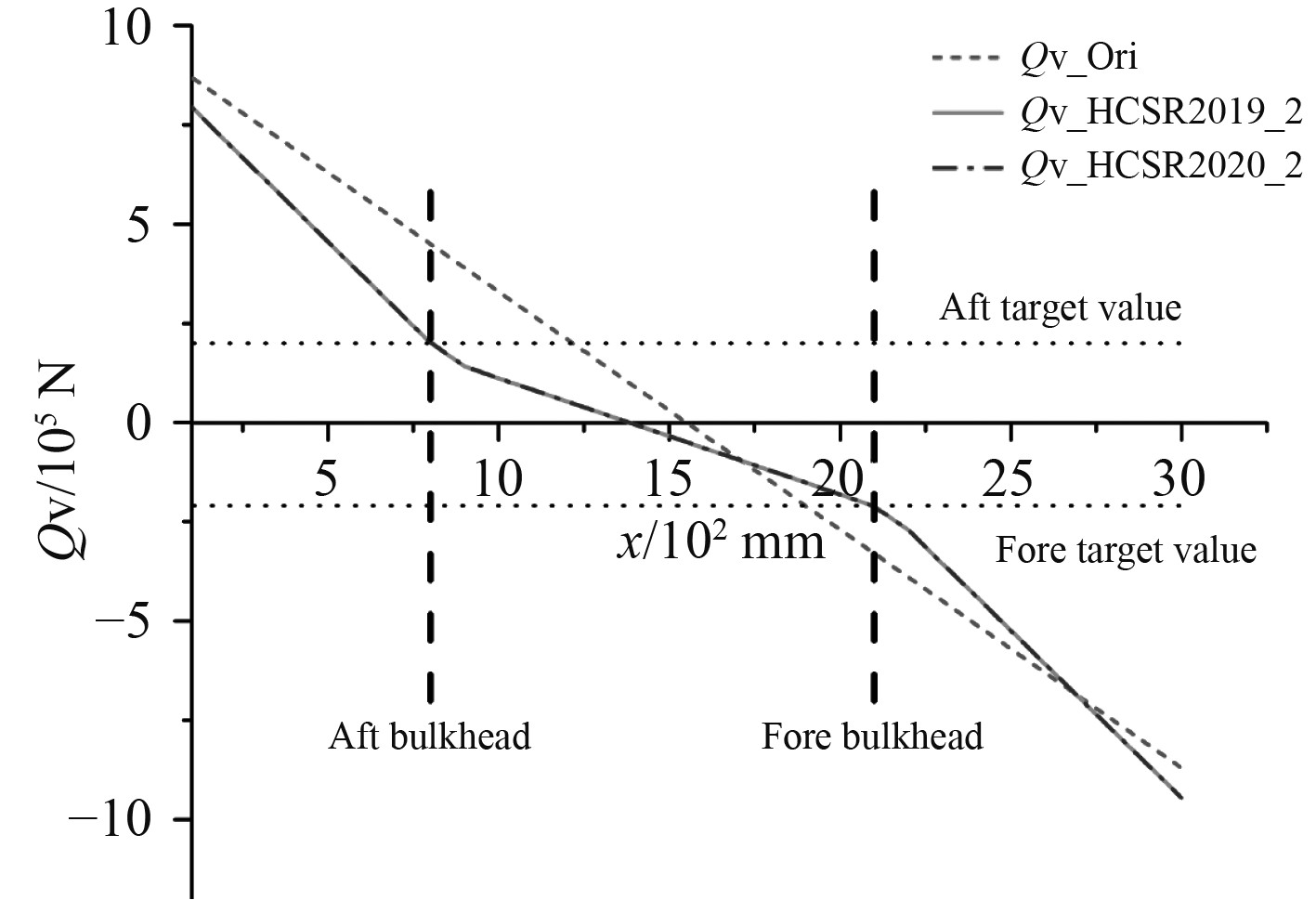
由图7和图8可知,相比于HCSR2019,HCSR2020除了将要求的位置的垂向剪力值调整至目标值外,还额外将尾端面的垂向剪力值(即尾端面支反力)调整为0。
|
图 8 HCSR2019和HCSR2020的方法2对比结果 Fig. 8 Comparison results between HCSR2019 and HCSR2020 in method2 |
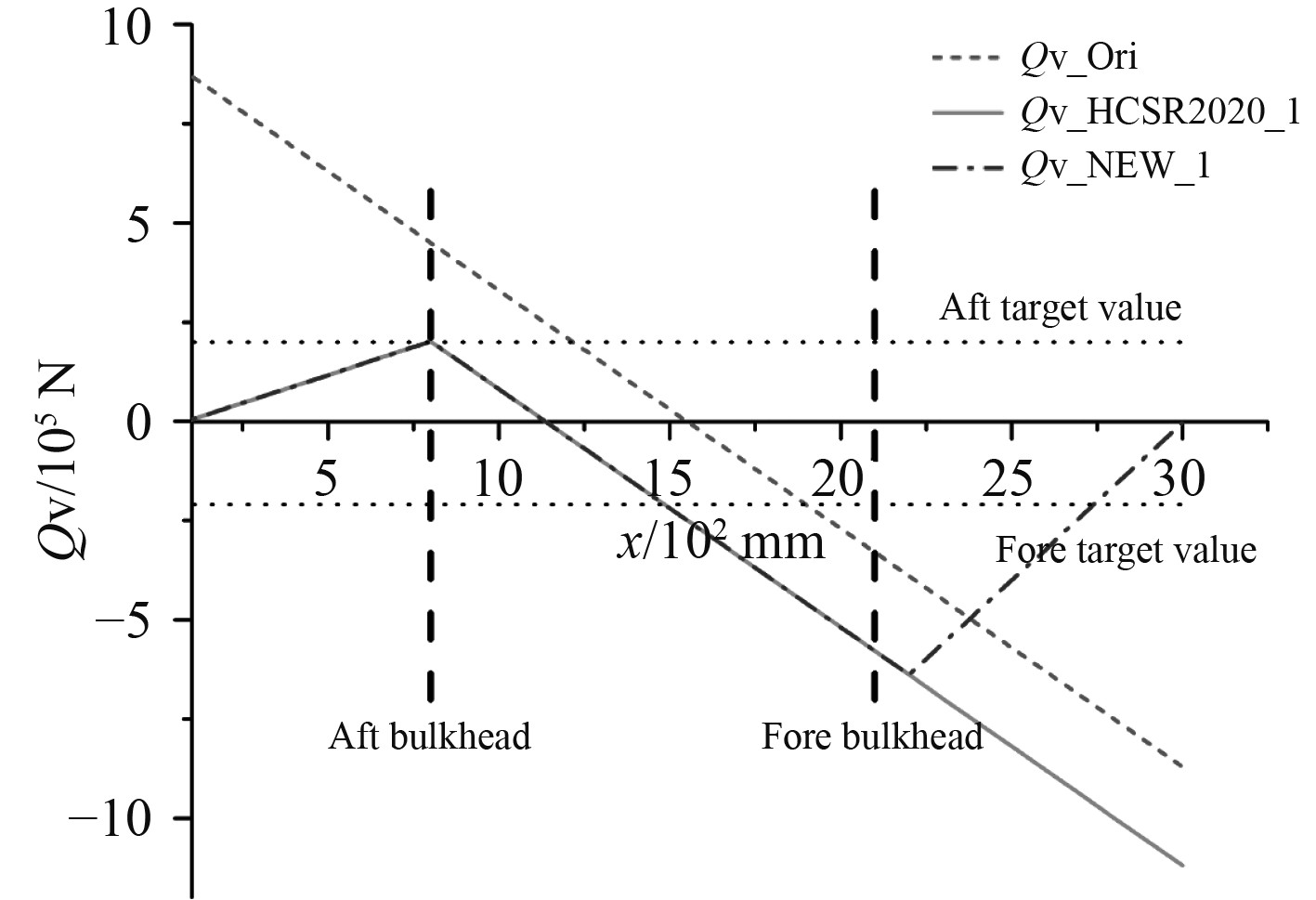
由图9和图10可知,相比于HCSR2020,本文的新方法除了将要求的位置的垂向剪力值调整至目标值外,还同时可以将首尾端面的垂向剪力值(即首尾端面支反力)均调整为0。
|
图 9 HCSR2020和本文新方法的方法1对比结果 Fig. 9 Comparison results between HCSR2020 and new method of the article in method1 |
通过对比HCSR2019和HCSR2020关于垂向剪力调整方法的不同,分析其背后的力学原理,并结合实际校核中遇到的问题,提出新的垂向剪力调整方法。与HCSR的方法相比,新调整方法除了可以将目标位置的垂向剪力值调整至目标值外,还同时可以将首尾端面的支反力均调整为0,避免模型首尾端面支反力过大对目标位置剪力校核结果的影响。
各垂向剪力调整方法对比结果如表1所示。
|
|
表 1 各垂向剪力调整方法对比表 Tab.1 Comparison between each vertical shear force adjustment method |
由于实船模型及工况的计算需要考虑后续的弯矩调整等工作(后续弯矩调整需要扣除由剪力调整引起的额外弯矩[9]),因此本次仅从理论和简化模型的数值上验证了本文提出的新方法的合理性,缺乏各方法对实际工况剪力校核结果的差异对比,接下来将针对实船模型以及实际的校核工况对新方法做进一步的验证。
| [1] |
张少雄, 李雪良, 陈有芳. 船舶结构强度直接计算中板单元应力的取法[J]. 船舶工程, 2004(3): 21-23. ZHANG Shao-xiong, LI Xue-liang, CHEN You-fang. Research on the stress in shell plate element in direct strength analysis of ship’s structure[J]. Ship Engineering, 2004(3): 21-23. DOI:10.3969/j.issn.1000-6982.2004.04.002 |
| [2] |
韩涛, 吴嘉蒙. CSR-H纵向不平衡力引起弯矩影响研究[J]. 船舶, 2018, 29(6): 123-128. HAN Tao, WU Jia-meng. Research on influence of moments caused by longitudinal unbalanced forces in CSR-H[J]. Ship & Boat, 2018, 29(6): 123-128. |
| [3] |
胡伟成. HCSR直接计算船体梁载荷研究[D]. 武汉: 武汉理工大学, 2013.
|
| [4] |
IACS. Common Structural Rules for Bulk Carriers and Oil Tankers[S]. IACS, 2019.1.
|
| [5] |
IACS. Common Structural Rules for Bulk Carriers and Oil Tankers[S]. IACS, 2020.1.
|
| [6] |
刘虓. 船舶结构力学[M]. 广州: 华南理工大学出版社, 2010.
|
| [7] |
IACS. Draft Technical Background for Rule Change Proposal 1 to 01 JAN 2019 version[S]. IACS, 2019.5.
|
| [8] |
唐旭东. 利用PCL语言查看船体剖面特性[J]. 船舶, 2011, 22(3): 27-29. TANG Xu-dong. Examination on hull section characteristics with PCL language[J]. Ship & Boat, 2011, 22(3): 27-29. |
| [9] |
肖茵茨. 40000DWT散货船舱段强度有限元分析[J]. 广东造船, 2012, 31(3): 52-54. XIAO Yin-ci. Finite element analysis on structural strength of cargo hold section for 40000dwt bulk carrier[J]. Guangdong Shipbuilding, 2012, 31(3): 52-54. |
 2022, Vol. 44
2022, Vol. 44
