声呐利用声信号来探测及定位的电子设备,安装于船首声呐平台内部。声呐的探测距离不仅取决于声呐本身的性能,同样与声呐所处环境的噪声水平有密不可分的联系,船首声呐平台内的噪声水平会直接影响声呐工作距离,即平台内自噪声水平越低声呐探测距离越远。船首声呐平台自噪声组成相对复杂,具体包括机械噪声、螺旋桨噪声、水动力噪声以及海洋环境背景噪声[1],机械噪声为主要噪声之一,其主要由舰船内部各种机械设备的振动而引发的噪声,此类噪声主要通过船体结构及舱室内流体传递至船首声呐平台。近年来越来越多的国内学者展开了相关研究,俞孟萨等[2]等分析了舰船首部声呐部位自噪声的特征,并较为全面地对首部和舷侧阵处声呐自噪声的预报及控制技术进行了综述。李东升等[3]等应用有限元法建立声呐平台数值模型,分析得出辐射噪声主要从平台底部及后部传递至基阵位置处。张洋波[4]基于有限元-边界元方法并结合实验方法,对某一导流罩模型在机械激励下的内部声场展开了研究,验证了有限元-边界元方法为处理封闭空间内部声场的有效方法。针对平台结构振动引起的低频自噪声,郭华林等[5]介绍了一种平台区低频自噪声预报方法。王祖华等[6]应用统计能量法预报了首部平台的自噪声并进行了模型试验。王毅娜等[7]利用统计能量法建立了声呐平台自噪声分析模型,并讨论了机械载荷和水动力载荷对自噪声特性的影响。庞福振等[8]针对吸声尖劈铺设方式、以及声波入射方式对平台内声学环境造成的影响进行了详细分析,并通过水下实验模型的验证,得出了吸声尖劈可有效改善平台内的声场分布,但是其降噪效果主要取决于非透声界面与透声窗的面积比例,因而存在较为明显的局限性。兰清[9]基于声学有限元法利用声呐平台局部模型对不同结构型式的声障板进行分析研究,得出凹角型声障板的性能相对较好,但并未将其应用于整船进行验证。船首声呐平台自噪声控制手段,其中包括在声呐平台内非透声界面铺设吸声材料或吸声结构、以及阻尼材料,这类措施的降噪效果除受到材料本身性能影响外,主要取决于透声窗面积与非透声界面比例,透声窗面积比例越大降噪效果越小。机械以及螺旋桨噪声主要是通过海水传递至声呐基阵处,声障板基于阻抗失配原理可有效阻截此类水载噪声。
本文基于统计能量法建立了船首声呐平台机械噪声仿真模型,并结合试验验证了凹角型声障板的降噪性能,同时仿真和试验结果两者间具有较好的一致性,表明了仿真模型的准确性与可行性。实际工程中开展此种类型的试验需要耗费相对较大的时间和成本,因此计算较准确且仿真周期短的船首声呐平台统计能量仿真模型,在实际工程应用中具有重要的指导意义。
1 理论基础统计能量法(SEA),是基于统计平均的概念,将结构按几何、物理等参数划分子系统,考虑子系统之间的能量传递,最终由能量方程求解得到各子系统平均能量的一种方法。
对于N个子系统组成的保守声-结构弱耦合系统,其功率流平衡方程的表达式如下[10]:其中:
| $\begin{split}& \omega \left[\begin{array}{cccc}\left({\eta }_{1}\text + {\displaystyle \sum _{i\ne 1}^{N}{\eta }_{1i}}\right){n}_{1}& -{\eta }_{12}{n}_{2}& \cdots & -{\eta }_{1N}{n}_{1}\\ -{\eta }_{21}{n}_{2}& \left({\eta }_{2}\text+{\displaystyle \sum _{i\ne 2}^{N}{\eta }_{2i}}\right){n}_{2}& \cdots & -{\eta }_{2N}{n}_{2}\\ \vdots & \vdots & \vdots & \vdots \\ -{\eta }_{N1}{n}_{N}& \cdots & \cdots & \left({\eta }_{N}\text+{\displaystyle \sum _{i\ne N}^{N}{\eta }_{Ni}}\right){n}_{N}\end{array}\right]\times\\ &\left\{\begin{array}{c}\dfrac{{E}_{1}}{{n}_{1}}\\ \dfrac{{E}_{2}}{{n}_{2}}\\ \vdots \\ \dfrac{{E}_{N}}{{n}_{N}}\end{array}\right\}=\left(\begin{array}{c}{P}_{1}\\ {P}_{2}\\ \vdots \\ {P}_{N}\end{array}\right) ,\\[-50pt]\end{split}$ | (1) |
在高频区域,当结构子系统的振动模态密集且重合度高,系统的动能和势能相差不大,结构子系统的总能量可以表示为:
| $ {E_i} = {M_i}\frac{{\displaystyle\sum\limits_j^{{N_i}} {{V_{ij}}^2} }}{{{N_i}}} = {M_i}\left\langle {{V_i}^2} \right\rangle。$ | (2) |
式中:
对于声腔子系统,当声腔摸态密度足够大时,声能与声腔空间的平均压力的平方成正比,这样声腔子系统的能量可表示为:
| $ {E_i} = \frac{{\left\langle {p_i^2} \right\rangle }}{{\rho {c^2}}}{V_i}。$ | (3) |
式中:
采用统计能量分析方法主要有2种频段划分方法,一种是依据子系统频段内的模态数N(Mode in band)进行划分:
| $ MOF = \frac{{{\Delta _{{1/ 2}}}{\omega _n}}}{{\delta \omega }} = \eta f \cdot n\left( \omega \right) = 2\zeta f \cdot n\left( \omega \right) ,$ | (4) |
当
船首声呐平台试验模型主体由空舱和水舱组成,模型最大尺寸为:长4.95 m,宽2.2 m,高2.16 m,模型最大重量为4.8 t,其中模型空舱上方有水密舱口盖和出线管,水舱采取沉浸式充水方式,水舱下方有水孔。试验过程中为保证模型下水时空舱与水舱保持平衡,使模型在水池中能基本保持水平的状态,在模型后端配备750 kg负载。试验模型采用B&KTYPE4826激振器来模拟机械激励,机械激励加载位置为平台空舱的前舱壁。
为模拟消声环境将试验模型放置于消声水池,其中水池的6个方向均进行消声处理,具体措施为:水池的四面墙壁及底部铺设固定式的吸声尖劈,水面上铺设可拆卸式的吸声尖劈。对船首声呐平台试验模型测试时放置在消声水池的位置及基阵处的测点位置,如图1所示。
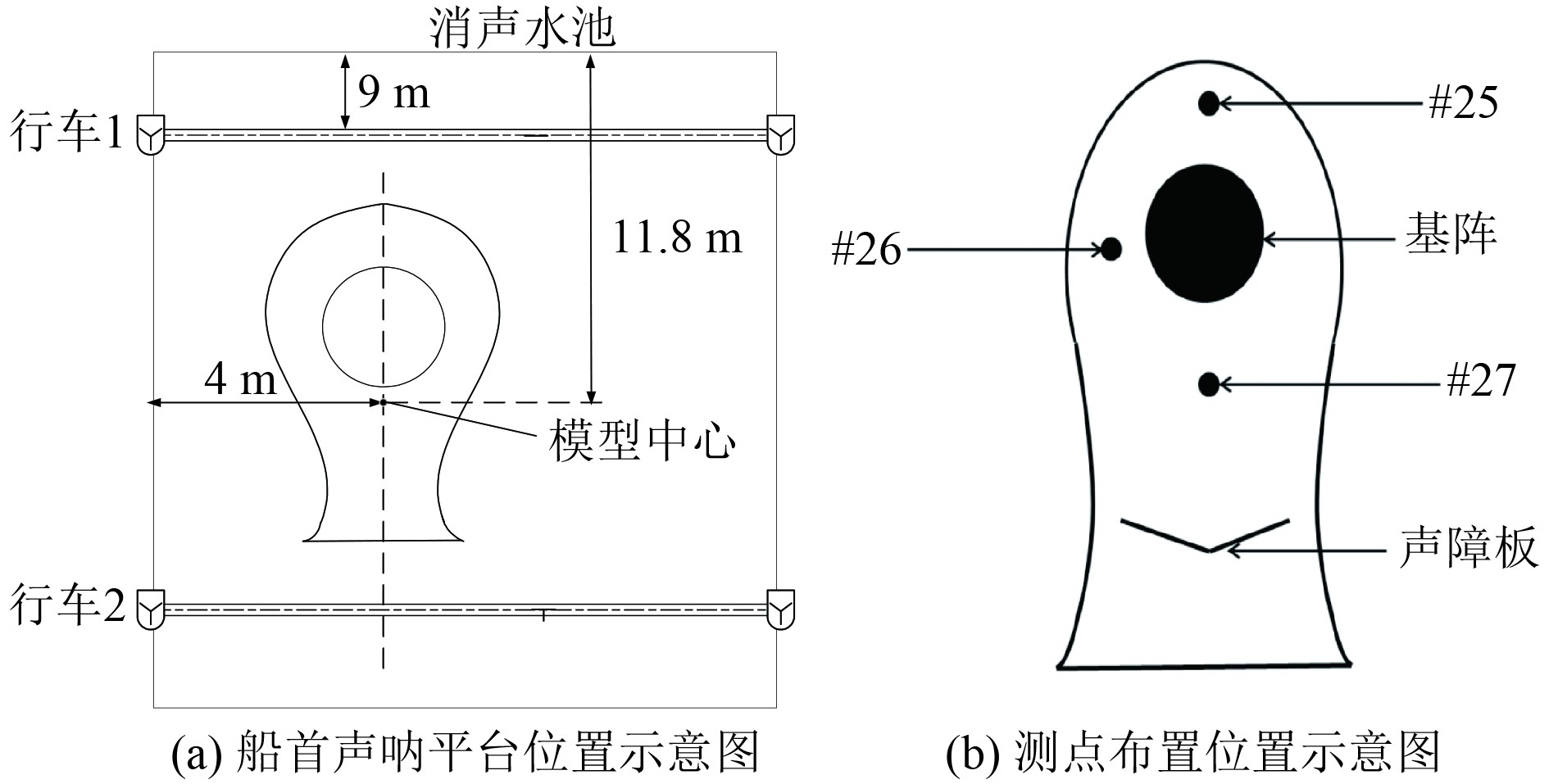
|
图 1 船首声呐平台位置以及测点布置位置示意图 Fig. 1 Schematic diagram of ship's sonar platform position and measuring point arrangement position |
船首声呐平台测点处的试验结果如图2所示。可知各测点位置处的声压级曲线变化趋势基本一致,由于3个测点与机械激励加载位置距离各不相同,因而距机械激励稍近的测点27的声压级明显高于其他2个测点的值。
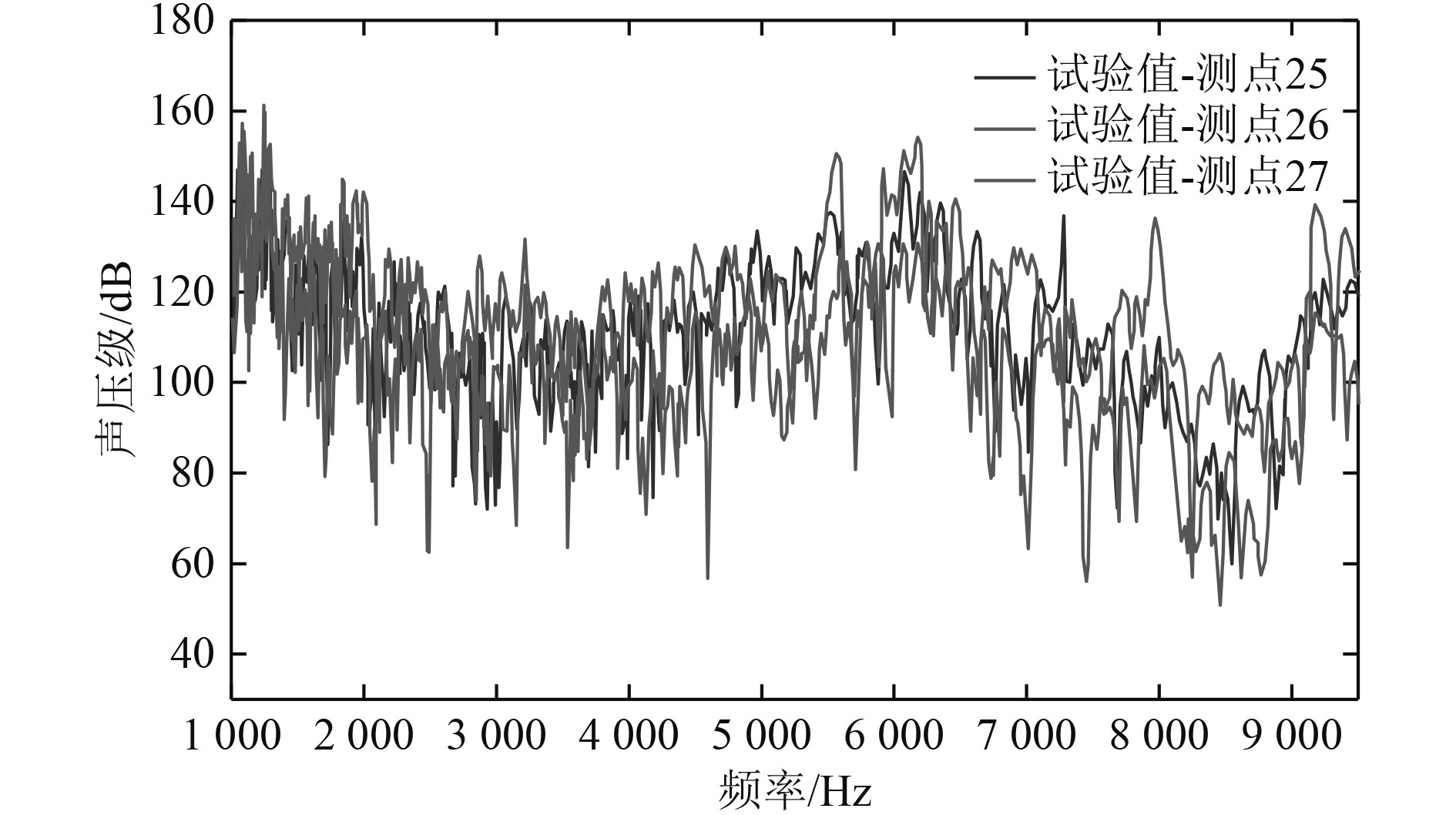
|
图 2 船首声呐平台测点处试验结果 Fig. 2 Experimental results at measurement points of bow sonar platform |
对凹角型声障板降噪性能进行试验验证,将声障板安装于声呐基阵与后舱壁之间(与仿真安装位置一致)。设置凹角型声障板前、后,各测点处的声压级变化曲线如图3所示,具体表现为测点25处的声压级降低了15 dB左右,测点26处的声压级降低了8 dB左右,测点27处的声压级降低了11 dB左右,其中测点25处的降噪效果相较于其他两侧点较好,主要是由于基阵的圆筒结构阻挡了部分声能的传递,试验结果表明凹角型声障板可有效控制船首声呐平台内的机械噪声。
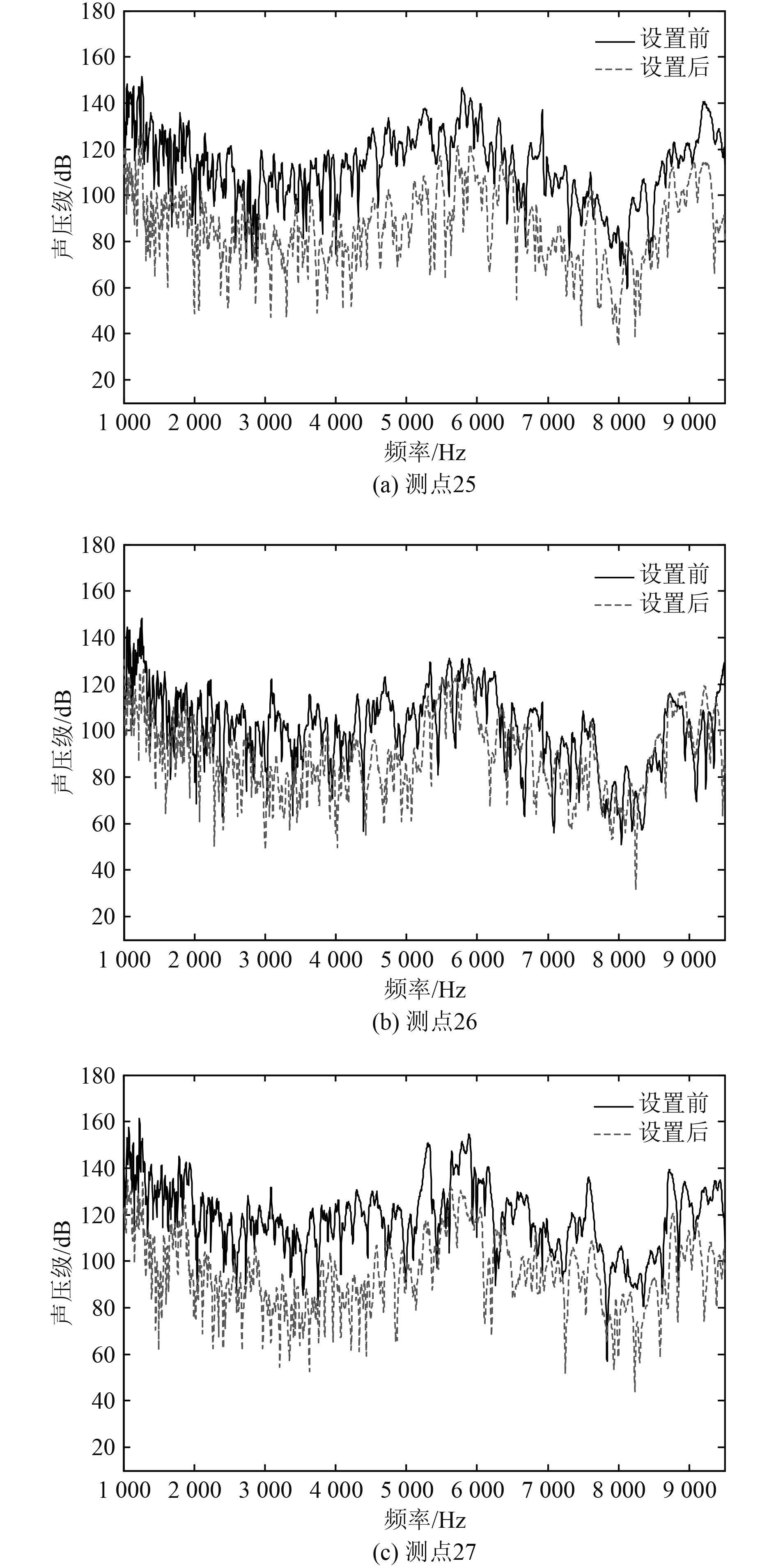
|
图 3 声障板设置前后三测点处声压级曲线对比图 Fig. 3 Comparison of sound pressure level curves at three measurement points before and after acoustic baffle setting |
基于统计能量法建立了船首声呐平台仿真模型,并采用VAOne中的点力模块来模拟试验的机械噪声源(机械激励为提取的试验机械激励数据),船首声呐平台仿真模型及机械激励加载位置,如图4(c)所示。其中仿真模型所选材料与试验模型保持一致,具体材料参数为表1所示。
|
|
表 1 仿真模型材料参数 Tab.1 Material parameters of simulation model |
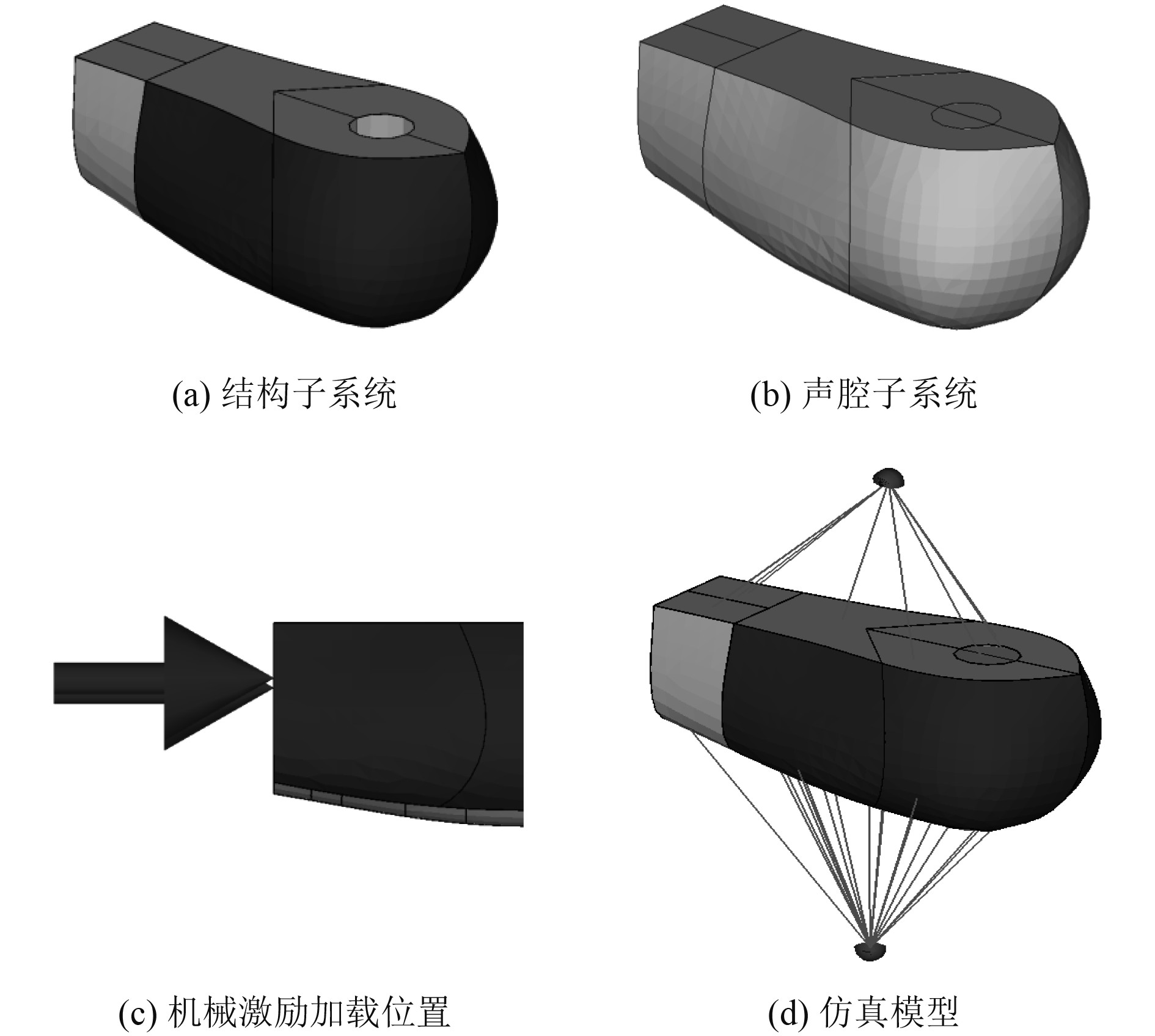
|
图 4 船首声呐平台仿真模型 Fig. 4 Simulation model of ship's sonar platform |
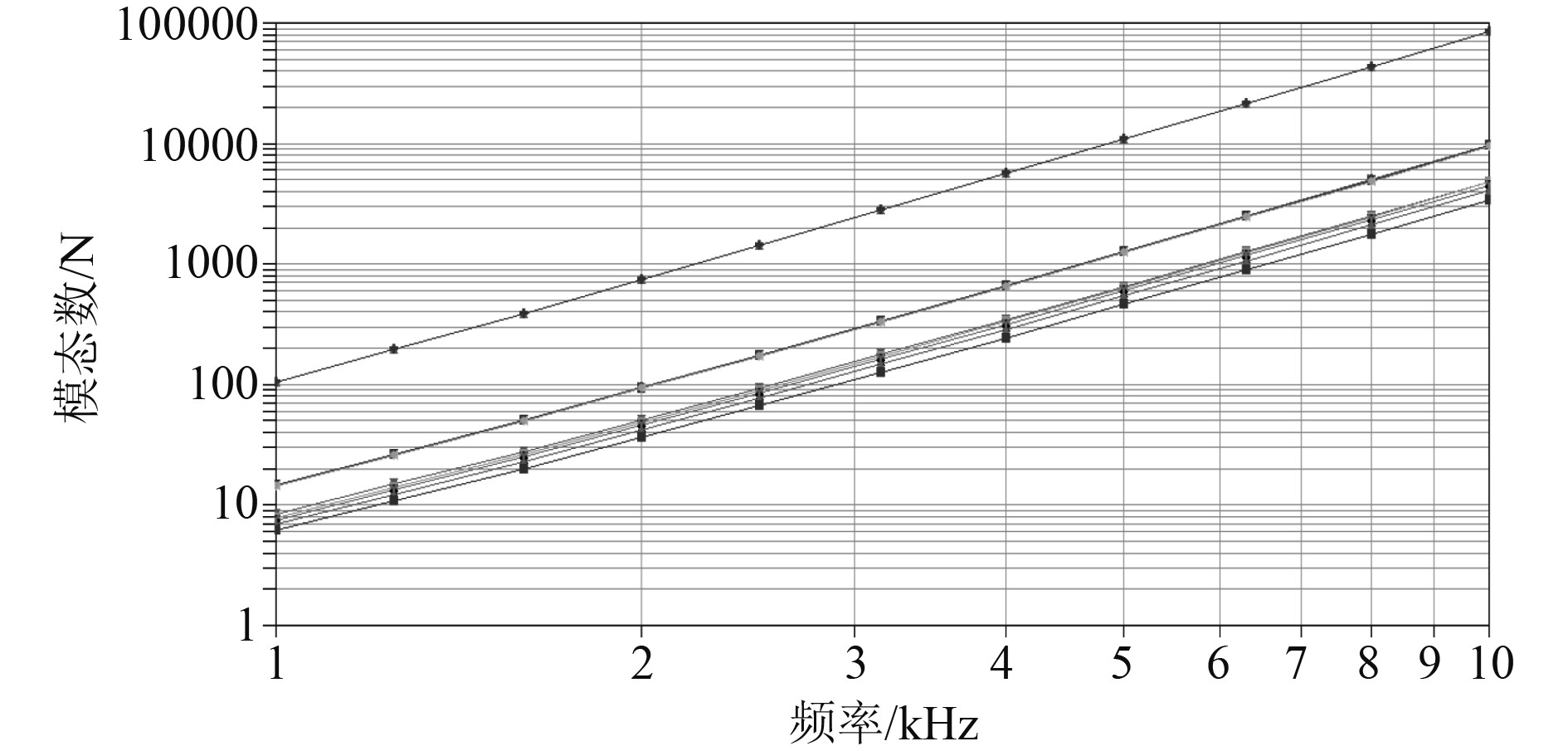
船首声呐平台局部仿真模型,共有88个结构子系统、17个声腔子系统以及2个半无限流体子系统,其中半无限流体子系统用于模拟沉浸式的充水方式以及无反射边界。船首声呐平台局部仿真模型的声腔子系统模态数如图5所示,可知在计算分析频段内声腔模态数都大于5,因而满足统计能量法的计算精度。
|
图 5 船首声呐平台各子系统模态数 Fig. 5 Mode number of each subsystem of ship's sonar platform |
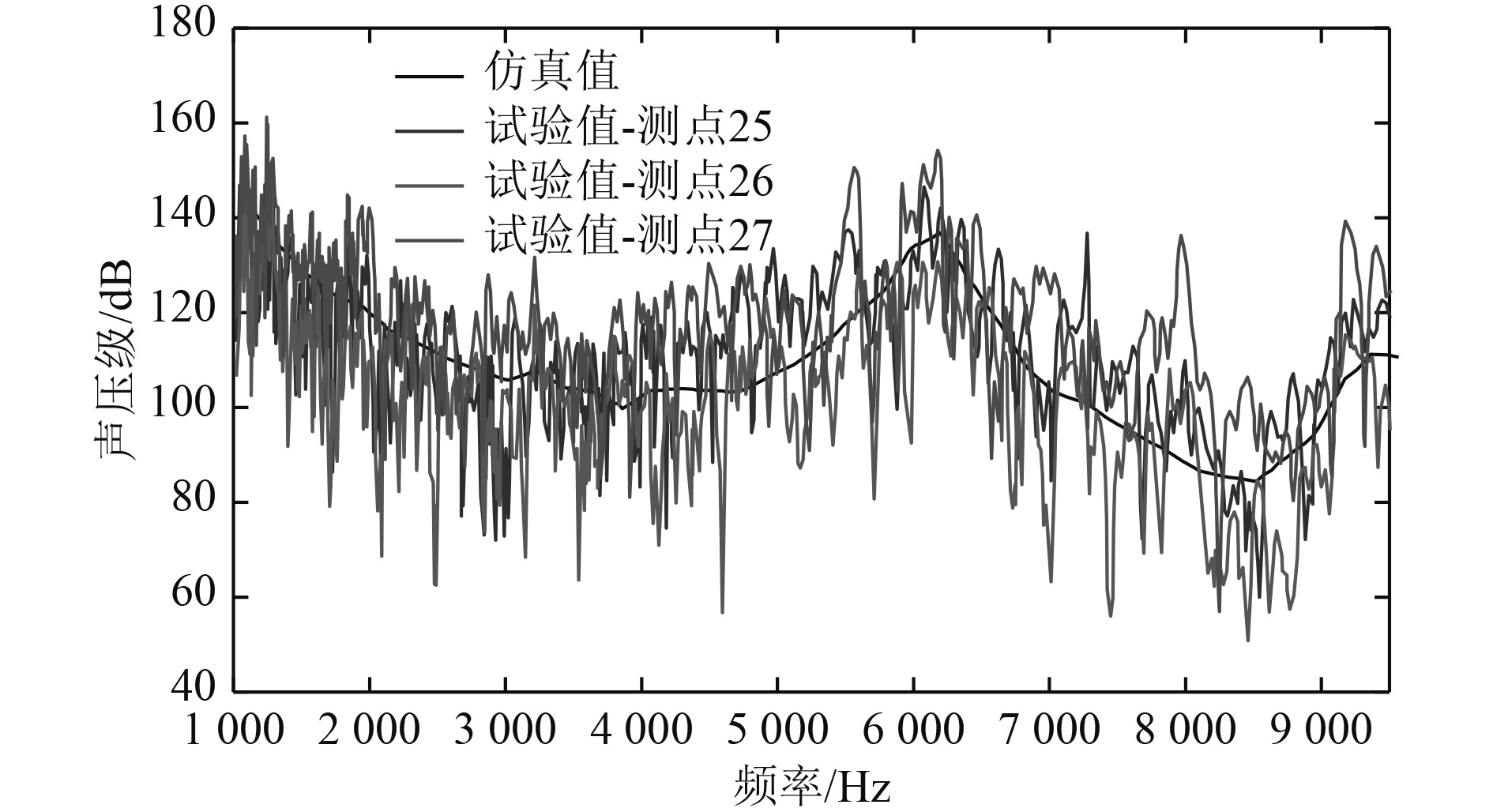
船首声呐平台测点处的试验结果与仿真值对比如图6所示,可知各测点位置处的声压级曲线变化趋势基本一致。由于3个测点与机械激励加载位置距离各不相同,因而距机械激励稍近的测点27的声压级明显高于其他2个测点的值。此外,试验结果与仿真值的声压级曲线变化趋势基本相同,且两者结果吻合较好,即验证了船首声呐平台局部仿真模型的正确性与可行性,为凹角型声障板的性能仿真研究奠定了基础。
|
图 6 试验结果与仿真值对比 Fig. 6 Comparison of test results with simulation values |
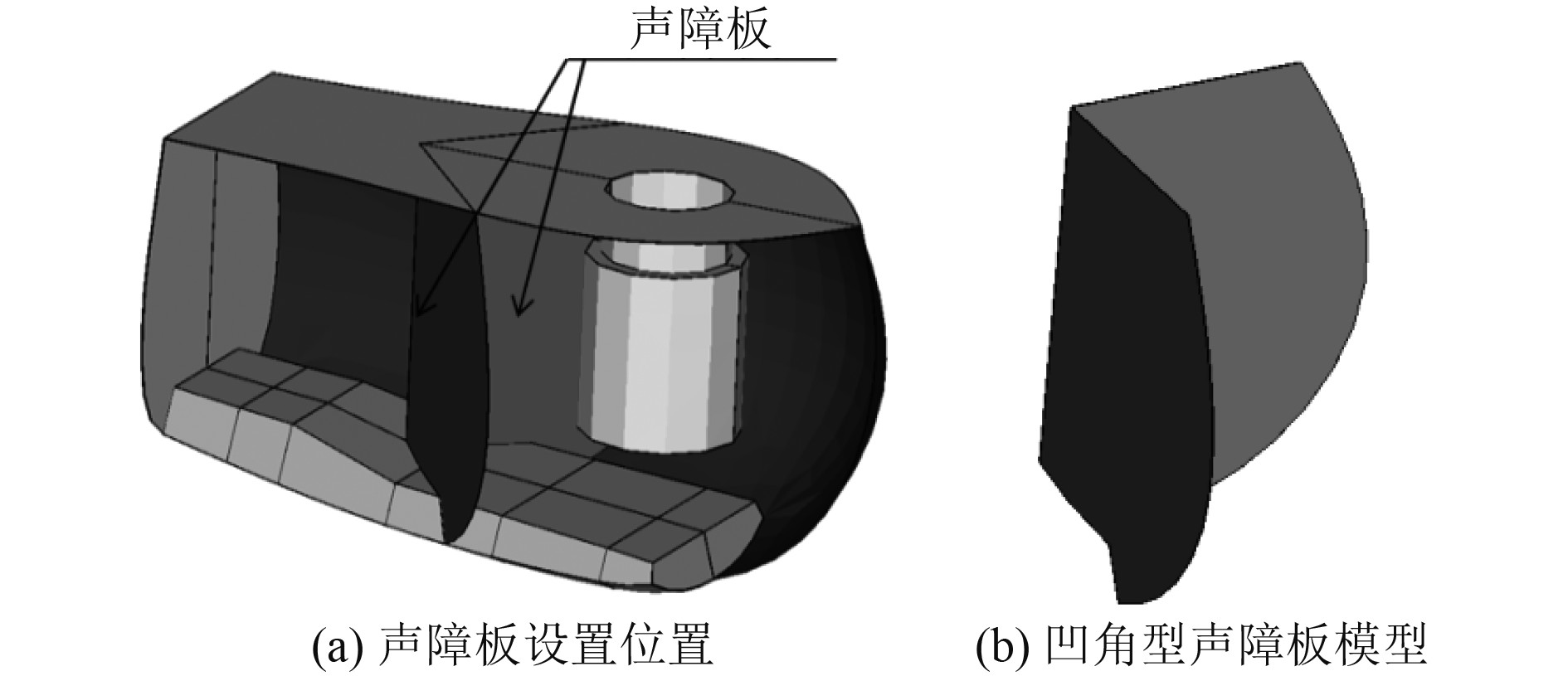
对凹角型声障板降噪性能进行仿真分析,其中船首声呐平台凹角型声障板仿真模型是在原有模型的基础上增设凹角型声障板,依据文献[7]可知凹角型声障板相较于其他型式的声障板具有更好的降噪效果,因此在基阵与后舱壁之间设置声障板,研究其对声呐平台内自噪声产生的影响。凹角型声障板性能仿真以及实验模型如图7所示,其中凹角型声障板由前部吸声层、中间层钢板、后部阻尼层3部分组成,总厚度为0.12 m。
|
图 7 声障板模型及设置位置 Fig. 7 Acoustic baffle model and position |
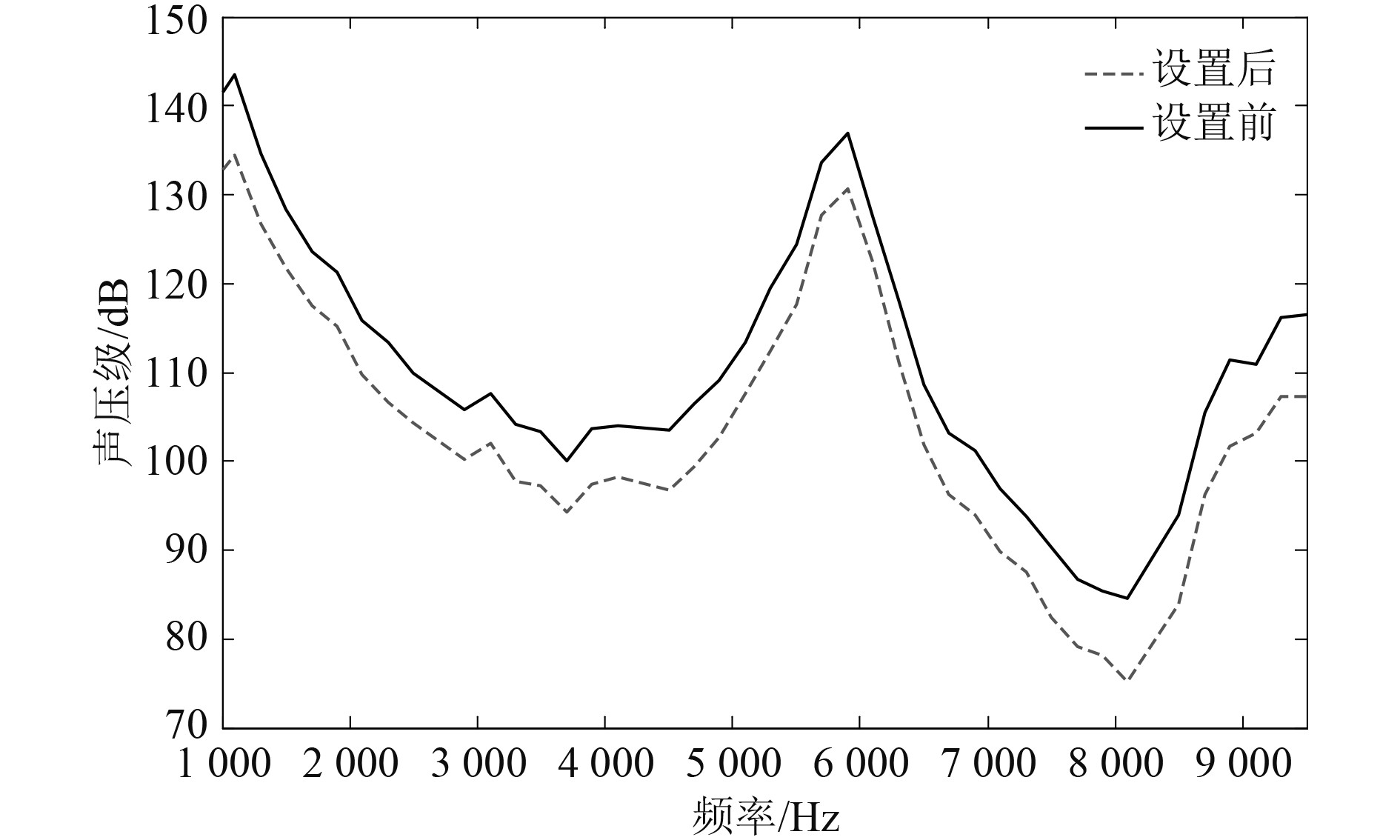
凹角型声障板设置前、后,船首声呐平台内仿真结果对比见图8所示。结果表明设置凹角型声障板后,船首声呐平台内噪声在整个试验频段内降低了10 dB左右,且随着频率的增加,降噪效果有逐渐提高的趋势。这是由于凹角型声障板对平台后舱壁的噪声起到了一定的阻隔及反射作用,降低了向声呐基阵处辐射的噪声,且随着频率减小声波的波长会逐渐增大,易在声障板边缘发生衍射效应从而导致声波绕过障板,因而频率越高凹角型声障板降噪性能越好。
|
图 8 声障板设置前后船首声呐平台内声压级曲线对比图 Fig. 8 Comparison of sound pressure level curves in the ship's sonar platform before and after acoustic baffle setting |
通过对凹角型声障板降噪性能仿真可知,凹角型声障板对船首声呐平台局部模型内的机械噪声有较为良好的控制效果,因而将凹角型声障板应用于基于整船的船首声呐平台模型中对机械噪声的降噪效果展开分析。整船基本参数为船舶总长135 m,舷宽16 m,吃水深度4.5 m,总吨位4200 t,其中机械设备主要包括主机、辅机、空压机以及空调机。基于整船的船首声呐平台仿真模型如图9所示。
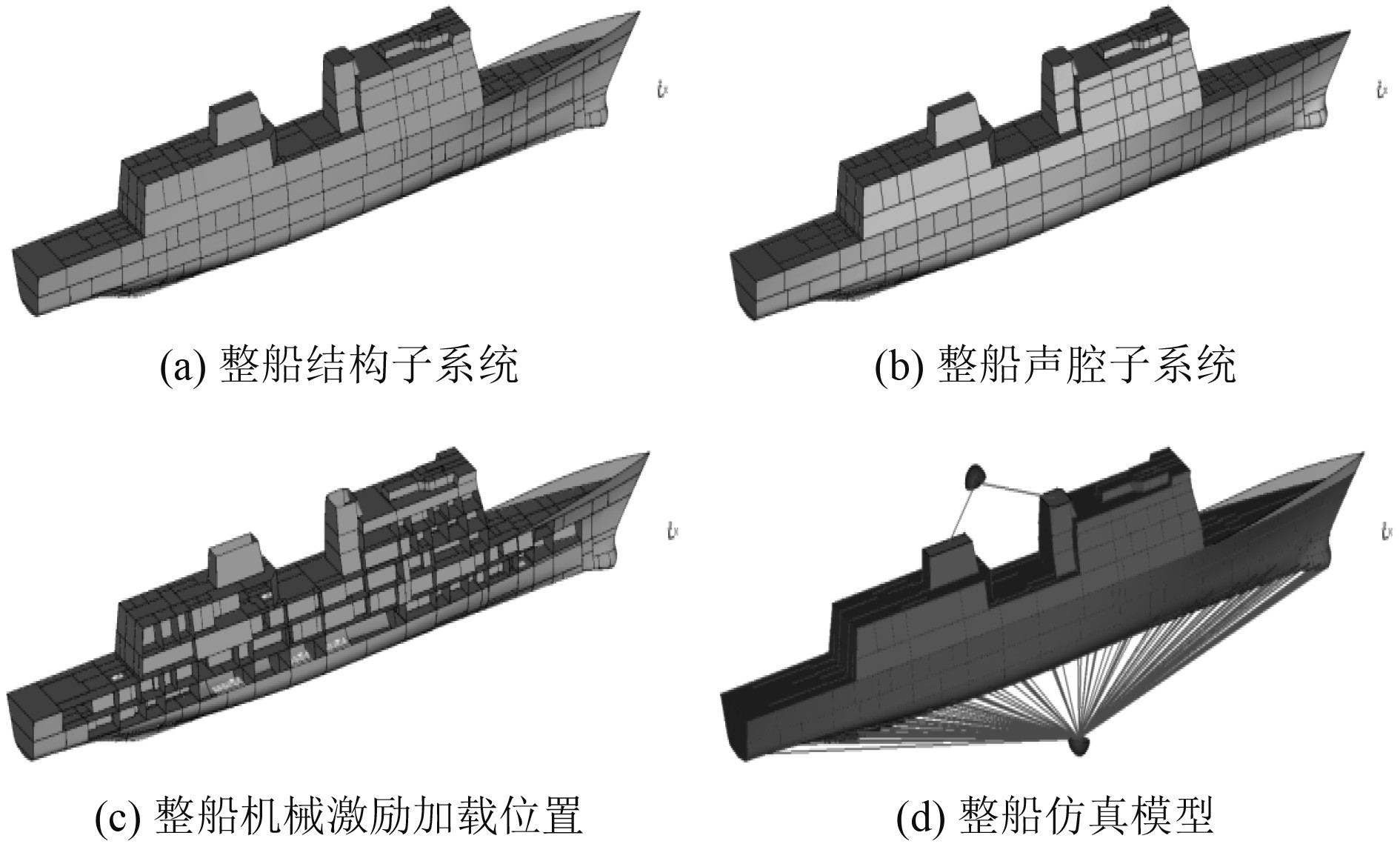
|
图 9 整船统计能量仿真模型 Fig. 9 Statistical energy simulation model for whole ship |
由图10可知,在整船的船首声呐平台中设置凹角型声障板,平台内机械噪声的降噪效果随着频率增加而逐渐提高,其中8 000 Hz处的降噪量可达7.5 dB左右。同时可以看出,凹角型声障板的降噪规律在整船和局部模型两者之间基本保持一致,但是降噪效果稍有差异,主要原因是整船与局部模型的结构以及机械激励源之间都存在较为明显差异。通过以上一系列研究可得,凹角型声障板对基于整船的船首声呐平台内的机械噪声依旧可以保持较好的降噪效果。
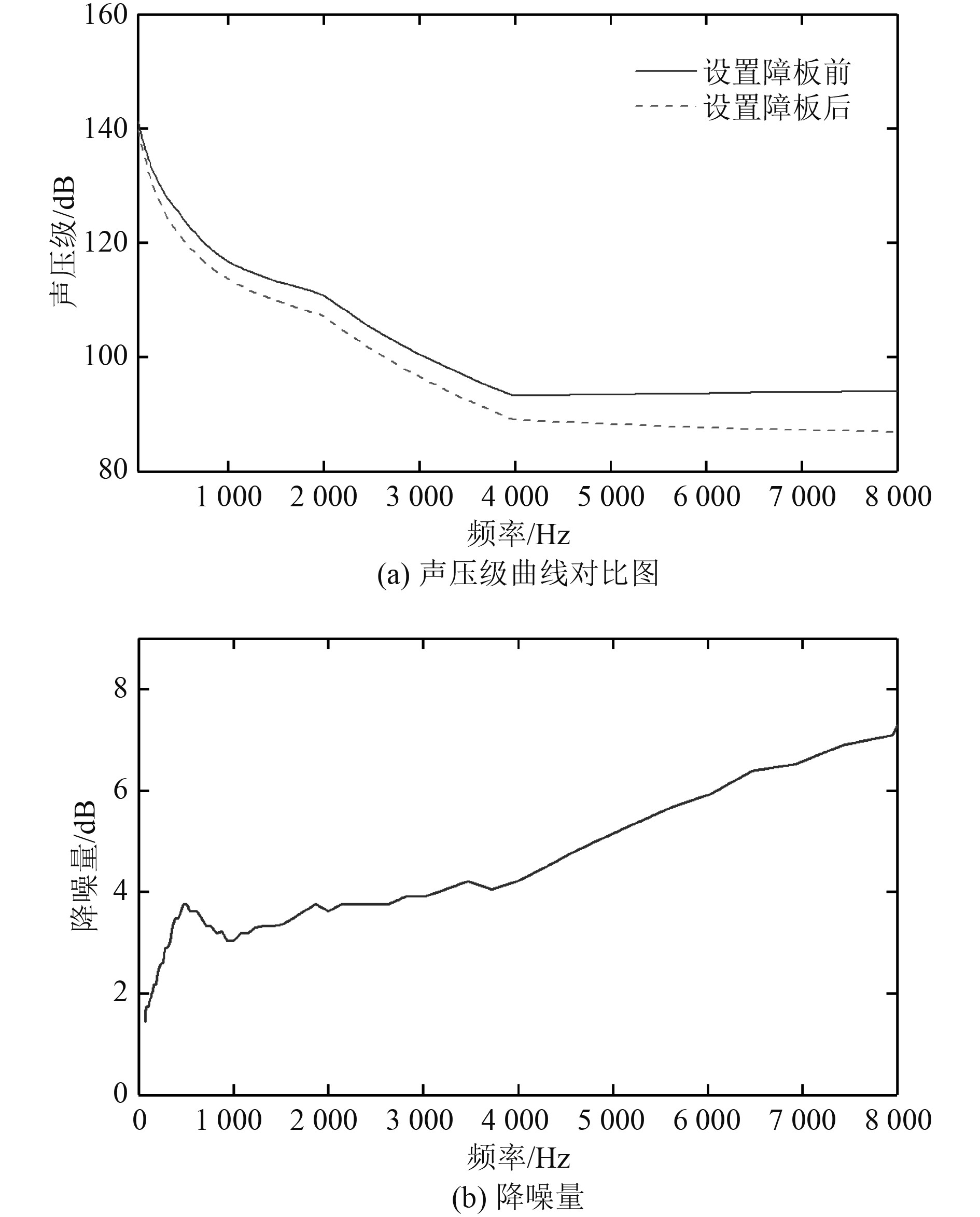
|
图 10 船首声呐平台内设置声障板前后降噪效果 Fig. 10 Noise reduction effect before and after setting acoustic baffle in the bow sonar platform |
本文以船首声呐平台为研究对象,从仿真与试验两方面对凹角型声障板的降噪性能展开分析。首先基于统计能量法建立了船首声呐平台机械噪声局部仿真模型,通过对比仿真与试验结果可知,两者在数值和变化趋势上具有较好的一致性,即验证了仿真模型的准确性以及开展凹角型声障板性能研究的可行性。进一步对比凹角型声障板性能的仿真值与试验结果可知,设置凹角型声障板可有效降低船首声呐平台局部模型内的机械噪声,其中在试验频段内可降低10 dB左右,最后将凹角型声障板应用于整船进行船首声呐平台内机械噪声降噪效果分析,结果表明其仍旧具有较为良好的降噪性能。
| [1] |
袁昌华. 潜艇低航速航行时的一种水下噪声源[J]. 舰船性能研究, 1990(2): 69-73. |
| [2] |
俞孟萨, 叶剑平, 吴有生, 等. 船舶声呐部位自噪声的预报方法及其控制技术[J]. 船舶力学, 2002, 6(5): 80-94. DOI:10.3969/j.issn.1007-7294.2002.05.012 |
| [3] |
李东升, 徐海宾, 蔡卫丰, 等. 声纳平台噪声控制机理分析[J]. 船舶力学, 2017, 21(7): 907-913. |
| [4] |
张洋波. 声纳导流罩内声场特性研究[J]. 声学技术, 2014, 33(5): 2014. |
| [5] |
郭华林, 骆东平, 陈美霞, 等. 潜艇首部声呐平台区低频自噪声预报方法[J]. 舰船科学技术, 2005, 27(4): 74-77. |
| [6] |
王祖华, 骆东平, 肖邵予. 潜艇首部声呐平台区中、高频自噪声预报[J]. 舰船科学技术, 2005, 27(5): 67-70. |
| [7] |
王毅娜, 庞福振, 苏楠, 等. 声纳平台自噪声特性及降噪措施优化研究[J]. 船海工程, 2014, 43(6): 44-47. DOI:10.3963/j.issn.1671-7953.2014.06.008 |
| [8] |
庞福振, 姚熊亮, 孙龙泉, 等. 敷设吸声尖劈的声纳平台水下声学特性实验研究[J]. 华中科技大学学报(自然科学版), 2011, 39(4): 106-109. |
| [9] |
兰清. 声纳平台自噪声控制方案研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [10] |
姚德源. 统计能量分析原理及其应用[M]. 北京: 北京理工大学出版社, 1995.
|
| [11] |
向育佳. 自航甲板货船舱室噪声预报及控制[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
 2022, Vol. 44
2022, Vol. 44
