2. 陆军军事交通学院镇江校区,江苏 镇江 212003;
3. 中国船舶科学研究中心,江苏 无锡 214082;
4. 上海船舶设计院,上海 201203
2. Army Military Transportation University of PLA, Zhenjiang Campus, Zhenjiang 212003, China;
3. China Ship Scientific Research Center, Wuxi 214082, China;
4. Shanghai Merchant Ship Design and Research Institute, Shanghai 201203, China
远洋船舶结构、水下耐压结构及海洋平台等都为大型焊接结构物,通常采用高强度钢或钛合金材料进行建造。对接焊是船舶与海洋结构物建造过程中最常用的一种焊接方式。焊接加工后的残余应力可能会对结构的力学性能产生一定的影响,并且焊接过程还有可能会使焊缝及热影响区域产生加工硬化现象。如果在焊接残余应力的计算过程中不考虑材料的加工硬化现象,就有可能使分析出来的结果与实际情况不符,从而导致后续结构力学性能分析的结果不合理,这会对大型船舶与海洋结构物的安全评估造成不利的影响。
在Lemaitre和Chaboche[1-2]提出的应变硬化模型的基础上,Smith等[3-7]应用混合硬化模型模拟了奥氏体不锈钢平板堆焊接头的残余应力。Sun等[8]研究了材料加工硬化行为对S355钢平板堆焊残余应力的影响。Deng等[9-10]通过SUS304奥氏体不锈钢的非线性硬化参数数据,研究了材料硬化模型对平板对接焊残余应力的影响。Wang等[11-12]采用二维数值模拟方法研究了材料硬化模型对高强度钢对接焊平板模型和超厚圆筒对接环焊模型残余应力的影响。总体上来说,目前有较少文献采用三维数值模拟方法研究硬化模型对高强度钢材料和钛合金材料对接焊残余应力的影响。
因此,本文采用三维数值模拟方法研究不同材料硬化模型分别对SUS304奥氏体不锈钢、屈服强度为918 MPa的高强度钢、Q345高强度钢和Ti80多层多道对接焊平板模型残余应力的影响,部分数值结果与文献试验数据进行了对比研究。研究结果可为大型船舶与海洋结构物工艺力学性能和结构安全可靠性分析提供相关的理论基础。
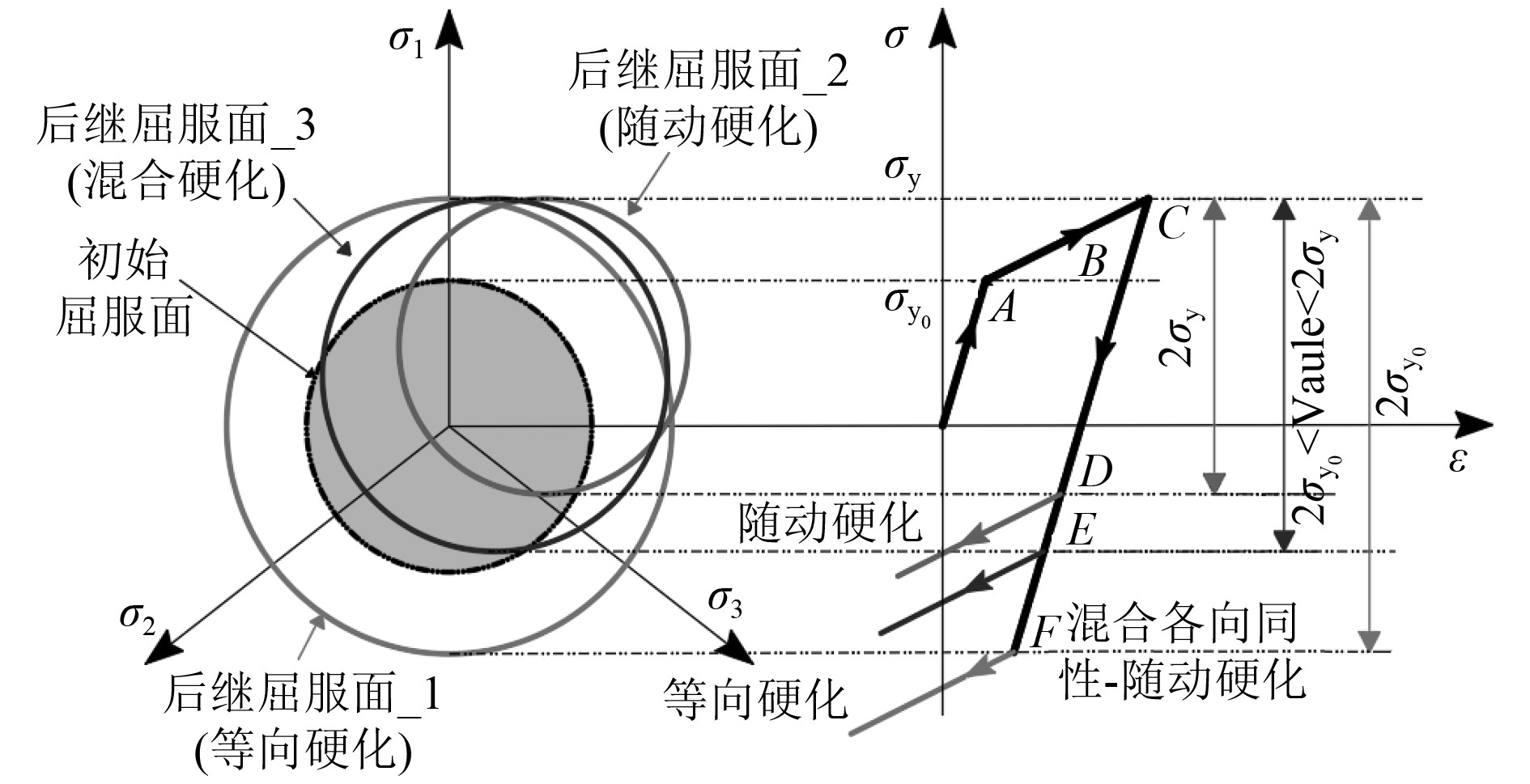
1 基本理论金属在塑性变形时,晶粒发生滑移,出现位错的缠结,使晶粒拉长,提高了材料的强度和硬度,这一阶段材料的抗变形能力得到了提高[13]。例如某些不锈钢材料,应变硬化率较高,硬化模型对焊接残余应力的影响较为明显。所以在某些情况下计算焊接残余应力时,需要考虑材料硬化现象对残余应力的影响。其中,目前常用的硬化模型主要有以下3种:等向硬化模型、随动硬化模型和混合硬化模型[5],它们的塑性模型对初始屈服强度和循环屈服强度的预测方式不同,如图1所示,
|
图 1 硬化模型原理示意图 Fig. 1 Schematic illustration of strain hardening models |
等向硬化模型假定后继屈服面的形状、中心和方位与初始屈服面相同,而后继屈服面的大小将随材料强化围绕初始屈服面中心均匀膨胀[14],使得屈服应力在塑性应变发生时在所有应力方向上增加(或减小)。在单轴拉伸加载后,压缩屈服应力F等于拉伸至屈服时获得的最大屈服应力值C,即|F|=|C|。其加载函数可以表示为[15]:
| $ f\left(\sigma \right)={\sigma }^{0}\left({\varepsilon }^{pl},\theta \right)。$ | (1) |
其中:
随动硬化模型假设后继屈服面是初始屈服面仅做刚体运动后形成的,该屈服面的形状、大小和方向均保持不变,只是屈服面中心位置移动了一段距离。随动硬化模型在初始加载方向的后继屈服极限提高了,而在其反方向的后继屈服极限却降低了。这表明随动硬化模型能够反映材料的包辛格效应。
1.3 混合硬化模型混合硬化模型允许屈服面扩张或收缩并同时平移,反向加载后,压缩屈服应力|E|介于等向硬化模型|D|和随动硬化模型|F|之间(图1中|D|<|E|<|F|)。混合硬化模型通常通过Lemaitre-Chaboche[1-2]公式描述,包含了等向硬化和非线性随动硬化2个成分。其中,等向硬化成分描述了屈服面半径的变化过程,其函数形式可以表示为:
| $ {\sigma ^0} = {\sigma _{|0}} + {Q_{\inf }}\left( {1 - {e^{ - b\overline \varepsilon pl}}} \right)。$ | (2) |
其中:
非线性随动硬化成分的函数形式可以用下式表示:
| $ \dot \alpha {\text{ = }}\sum\nolimits_i \left[ {C_i}\frac{{\text{1}}}{{{\sigma _{\text{0}}}}}\left( {\sigma {{ - }}\alpha } \right){{\dot {\bar \varepsilon} }^{pl}}{{ - }}{\gamma _i}\alpha {\dot {\bar \varepsilon} }^{pl} \right]。$ | (3) |
其中:
通常材料的等向硬化和随动硬化参数数据较容易获得,并且相比混合硬化模型计算时间短,在复杂工况或者大型结构计算过程中使用等向硬化模型和随动硬化模型的需求较多、实用性较强,所以本文研究针对等向硬化模型、随动硬化模型和理想弹塑性模型展开对接焊平板残余应力的影响研究。
2 加工硬化对SUS304对接焊平板残余应力影响研究为了更好地进行后续加工硬化对高强度材料对接焊残余应力的影响研究,对文献[9]中的对接焊平板残余应力进行模拟和试验结果比对研究。
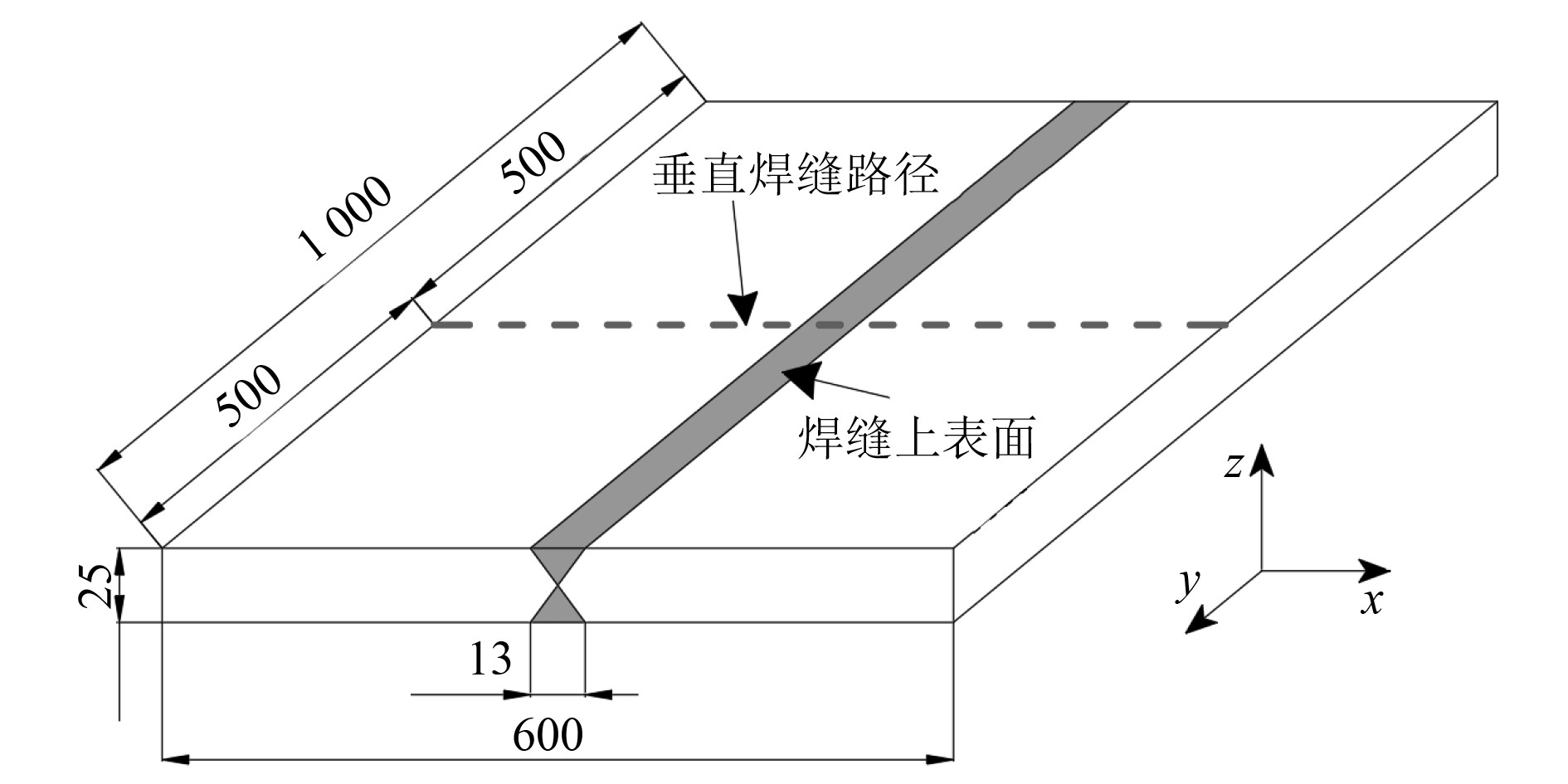
SUS304对接焊平板模型[9]由2块长度、宽度和厚度分别为1 000 mm,300 mm和25 mm的平板焊接而成,焊缝为双V型坡口,焊后表面焊缝宽度为13 mm,如图2所示。有限元模型的焊缝及热影响区附近的网格较为密集,远离焊缝处网格逐渐稀疏。SUS304对接焊平板模型的材料参数、焊接工艺参数和边界条件等与文献[9]相一致。
|
图 2 SUS304对接焊平板示意图(mm) Fig. 2 SUS304 schematic diagram of butt welding plate |
基于热弹塑性热力学理论[16-17]、生死单元法和给定温度法[18-20],采用Ansys软件的APDL语言编制焊接残余应力有限元计算程序;分析理想弹塑性模型、等向硬化模型和随动硬化模型对对接焊平板残余应力的影响。
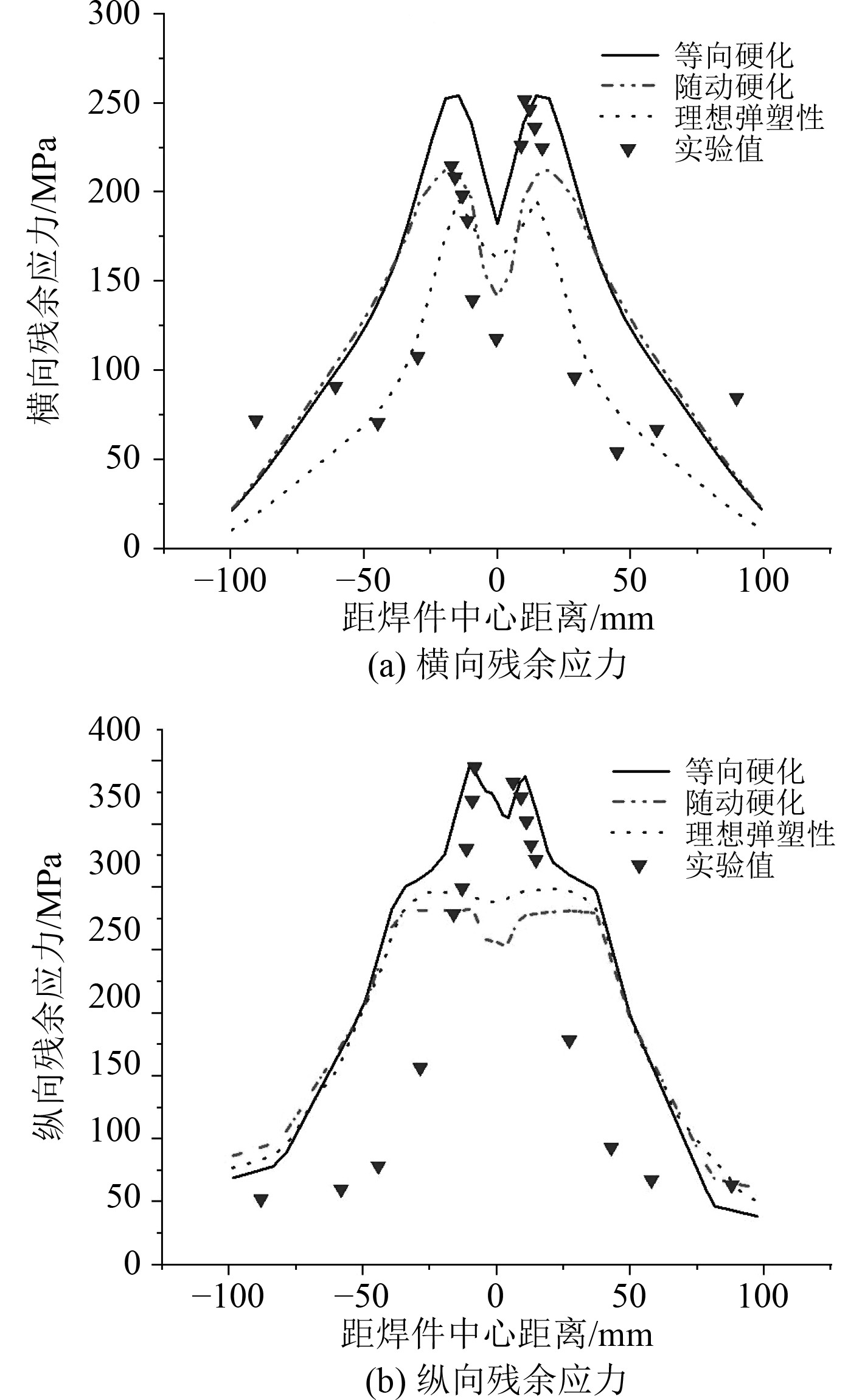
图3为SUS304对接焊平板上表面采用不同材料硬化模型的残余应力数值模拟及与文献[9]中的试验结果。
|
图 3 不同硬化模型的SUS304对接焊平板残余应力数值模拟和文献[9]中试验结果 Fig. 3 Numerical simulation of residual stress of SUS304 butt welding plate with different hardening models and experimental results in reference [9] |
可以看出,SUS304对接焊平板不同材料硬化模型的对接焊平板上表面垂直焊缝路径上。
1)如图3(a)所示,横向焊接残余应力呈现明显的双峰分布趋势,最大残余拉应力出现在焊缝热影响区附近;其中,采用等向硬化模型的横向拉残余应力预测结果最大,最大拉应力约为260 MPa,随动硬化模型次之,理想弹塑性模型最低。
2)如图3(b)所示,纵向残余应力在焊缝附近有较大的拉应力;采用等向硬化模型计算的纵向残余拉应力最高,最大值约为400 MPa,而随动硬化模型和理想弹塑性模型较低。
总体来说,本文采用的模拟方法与文献试验结果较为接近,纵向残余应力结果明显大于横向残余应力结果。采用等向硬化模型计算的焊接残余应力数值模拟结果与试验结果最为接近。所以,在分析SUS304对接焊平板残余应力时,采用等向硬化模型来分析焊接残余应力更合理,较为接近实际情况。
3 加工硬化对高强度材料对接焊平板残余应力影响研究在研究SUS304不锈钢平板对接焊残余应力结果与文献试验相一致的基础上,考虑不同材料硬化模型对高强度材料的对接焊平板残余应力进行研究。
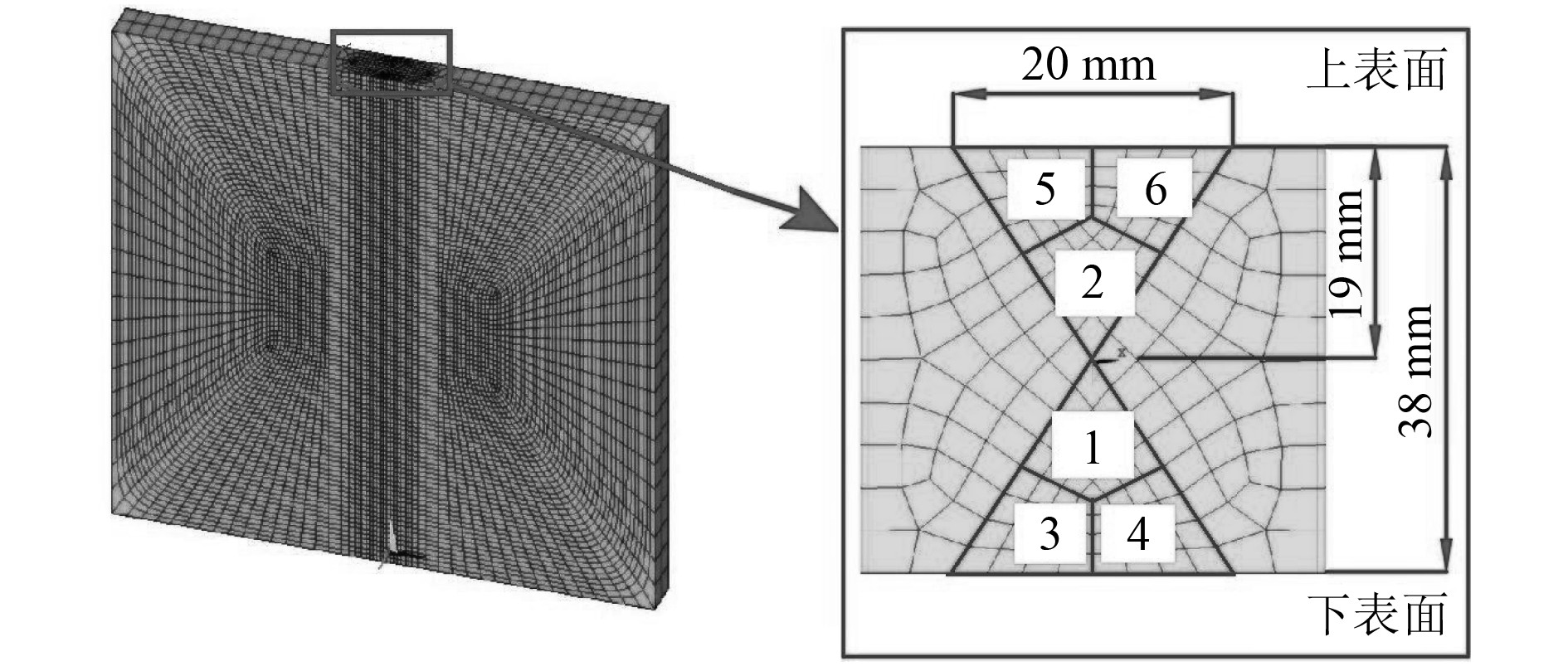
3.1 屈服强度为918 MPa的高强度钢屈服强度为918 MPa的高强度钢对接焊平板模型长度、宽度和厚度分别为500 mm、500 mm和38 mm,焊接坡口为双V型,表面焊缝宽度为20 mm,如图4所示。图5为焊接模型网格划分及焊道设置,焊接顺序为正反面坡口交替焊接,且焊接模型的材料参数、焊接尺寸和焊接工艺参数等与文献[2]相一致。
|
图 4 屈服强度为918 MPa高强度钢焊接件尺寸示意图(mm) Fig. 4 Schematic diagram of welding parts size of high strength steel with yield strength of 918 MPa |
|
图 5 网格划分及焊道分布设置 Fig. 5 Grid generation and weld bead distribution |
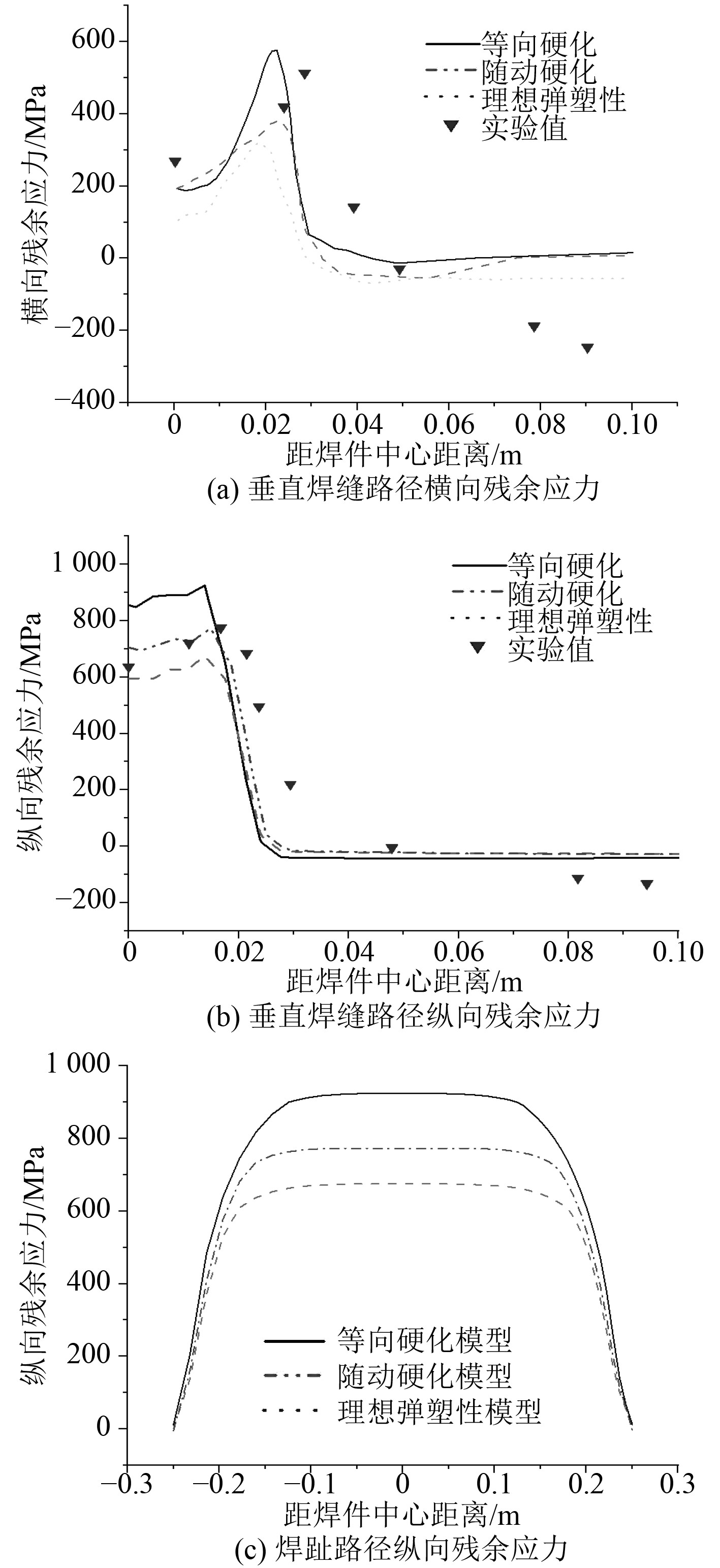
图6(a)和图6(b)显示了考虑不同材料硬化模型的对接焊平板上表面垂直焊缝路径横向和纵向残余应力数值模拟结果,并与文献数据对比;图6(c)显示了考虑不同材料硬化模型的对接焊平板上表面焊趾路径纵向残余应力分布。
|
图 6 不同硬化模型屈服强度为918MPa的高强度钢对接焊平板残余应力和试验结果 Fig. 6 Figure of welding residual stress with yield strength of 918MPa of different hardening criteria |
由图6可知,考虑不同材料硬化模型的屈服强度为918 MPa的高强度钢对接焊模型:
1)图6(a)中垂直焊缝路径横向焊接残余应力数值模拟结果呈现明显的双峰分布趋势,最大残余拉应力出现在焊缝热影响区附近。其中,采用等向硬化模型的横向拉残余应力预测结果最大,最大拉应力约为600 MPa;随动硬化模型次之,理想弹塑性模型最小。
2)图6(b)中垂直焊缝路径纵向残余应力数值模拟结果在焊缝部位表现为拉应力。理想弹塑性模型纵向残余拉应力最大值约为750 MPa;等向硬化模型的纵向残余应力最大值约为930 MPa,与理想弹塑性模型相比提高了约25%;随动硬化模型的纵向残余应力最大值约为780 MPa,与理想弹塑性模型较为接近。
3)图6(c)中沿焊趾路径纵向残余应力分布趋势相同,靠近焊缝中心处纵向残余应力数值差距较大。
总体来说,等向硬化模型得到的焊接残余应力结果更加合理。
3.2 Q345高强度钢Q345高强度钢对接焊平板模型尺寸与屈服强度为918 MPa的高强钢平板对接焊模型相同,材料采用Q345高强度钢,相关热物理性能和力学性能参数参考文献[21],其有限元模型网格划分、数值模拟方法和边界条件与屈服强度为918 MPa的高强钢平板对接焊模型相一致。
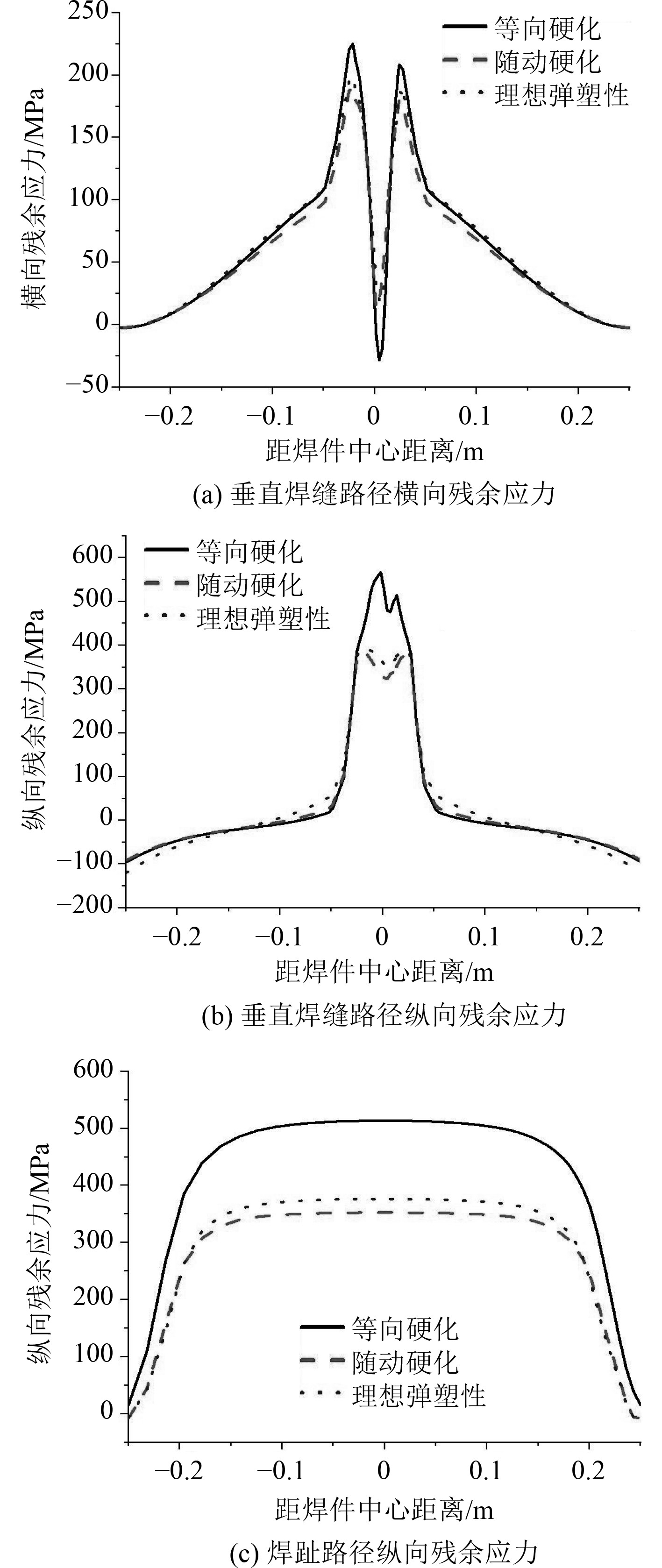
图7分别为不同硬化模型Q345对接焊平板模型垂直焊缝路径上横向、纵向残余应力和焊趾路径上的纵向残余应力。
|
图 7 不同硬化模型的焊接残余应力 Fig. 7 Welding residual stress distribution of different hardening models |
由图7可知,不同硬化模型下的Q345高强度钢对接焊平板模型:
1)图7(a)和图7(b)中横向和纵向残余应力在垂直焊缝路径上焊缝及热影响区处均表现为拉应力,呈双峰分布,横向残余应力最大值约为250 MPa,而纵向残余应力最大值约为550 MPa;等向模型的焊接残余拉应力均较大。
2)图7(c)中焊趾路径上的纵向残余应力表现为拉应力,最大值约为500 MPa,纵向焊接残余应力最大值大于横向焊接残余应力;从图7(b)和图7(c)可以看出,等向硬化模型的纵向焊接残余拉应力在焊缝附近较高,相比理想弹塑性模型和随动硬化模型增加了约45%。
总的来说,硬化模型对Q345对接焊平板模型表面横向焊接残余应力的影响不大,而对纵向焊接残余应力有较大的影响。
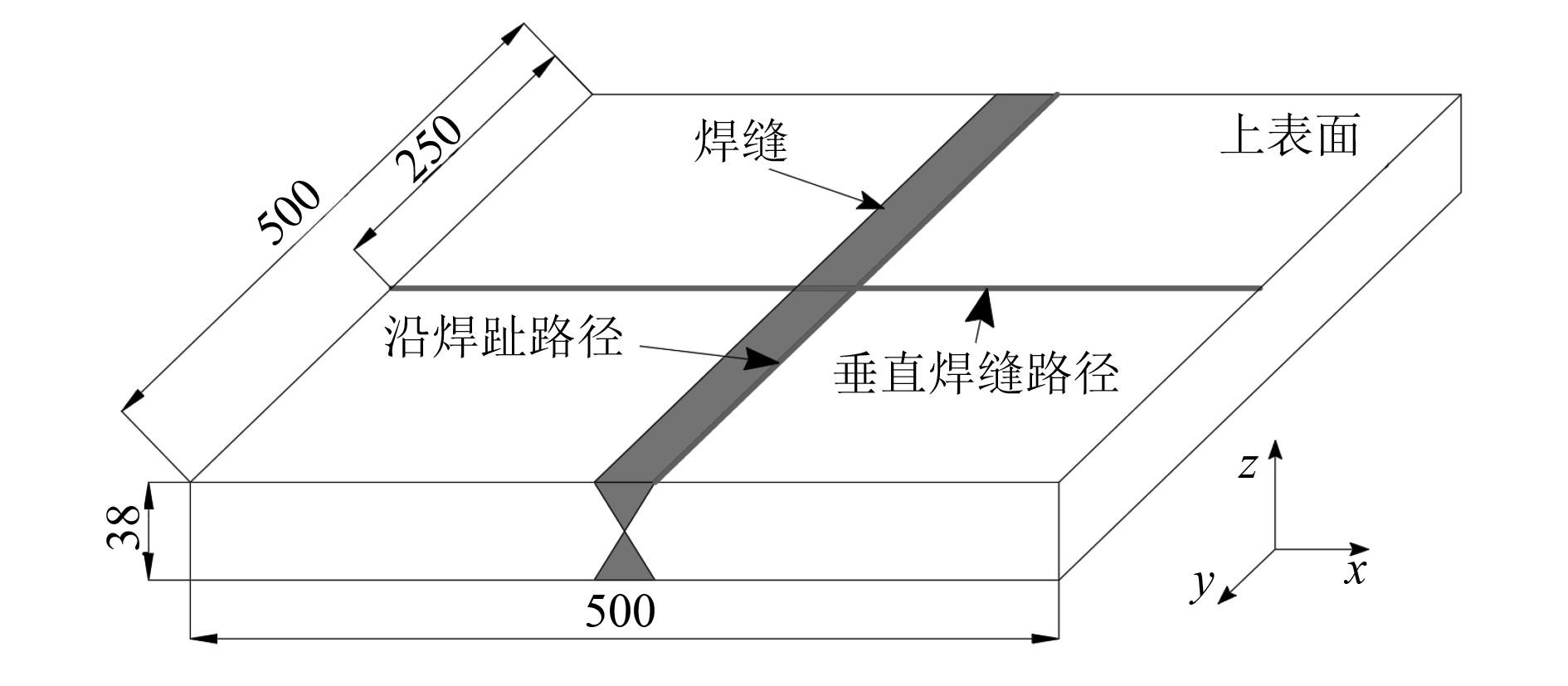
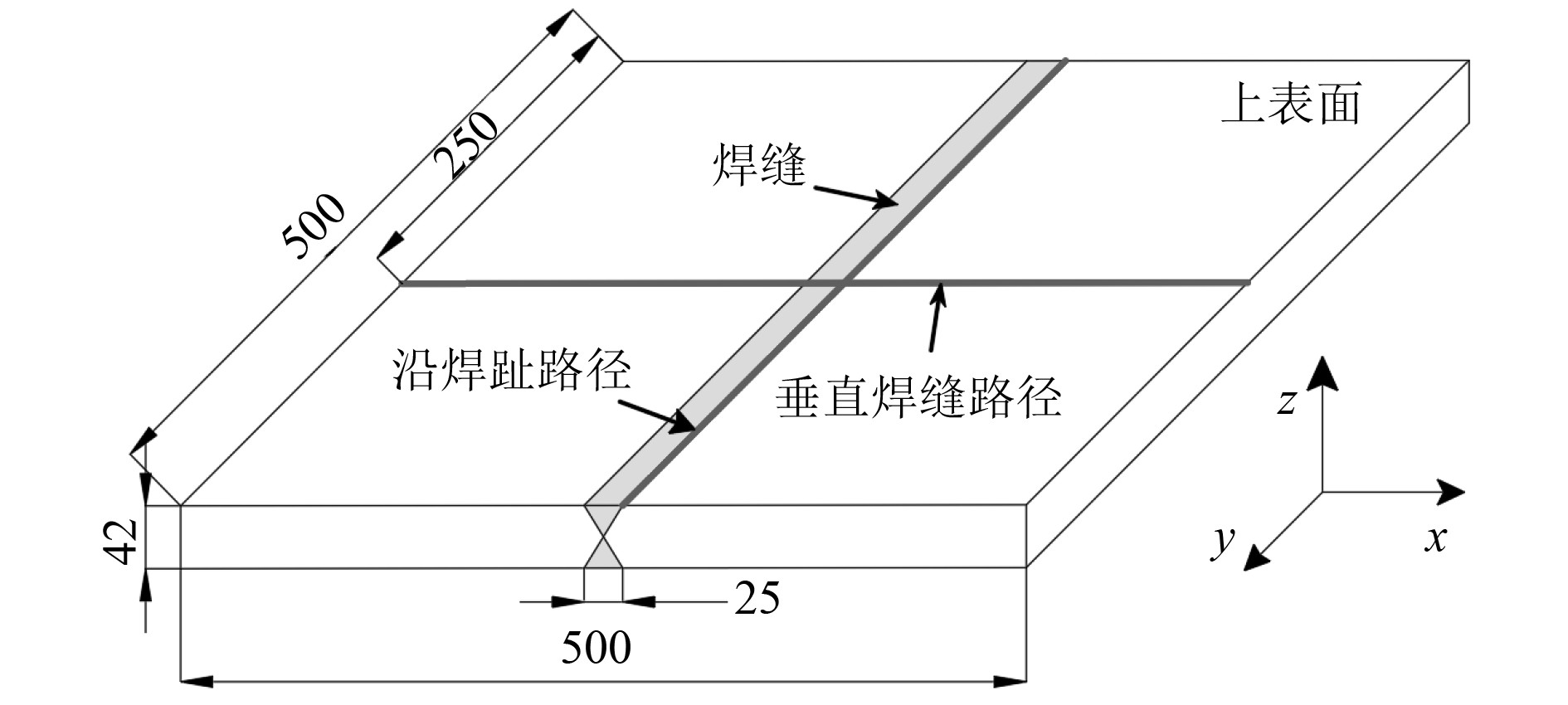
3.3 Ti80Ti80对接焊平板的长度、宽度和厚度分别为500 mm、500 mm和42 mm,焊接坡口为双V型,上下表面焊缝宽度分别为25 mm,如图8所示。焊接过程为正反面交替焊接,并与文献[22]保持一致。模拟使用的焊缝填充材料与焊板为同一种材料;材料的热物理性能参数、力学性能和焊接工艺参数均参考文献[22]。
|
图 8 Ti80焊接件尺寸示意图(mm) Fig. 8 Dimension diagram of Ti80 weldment |
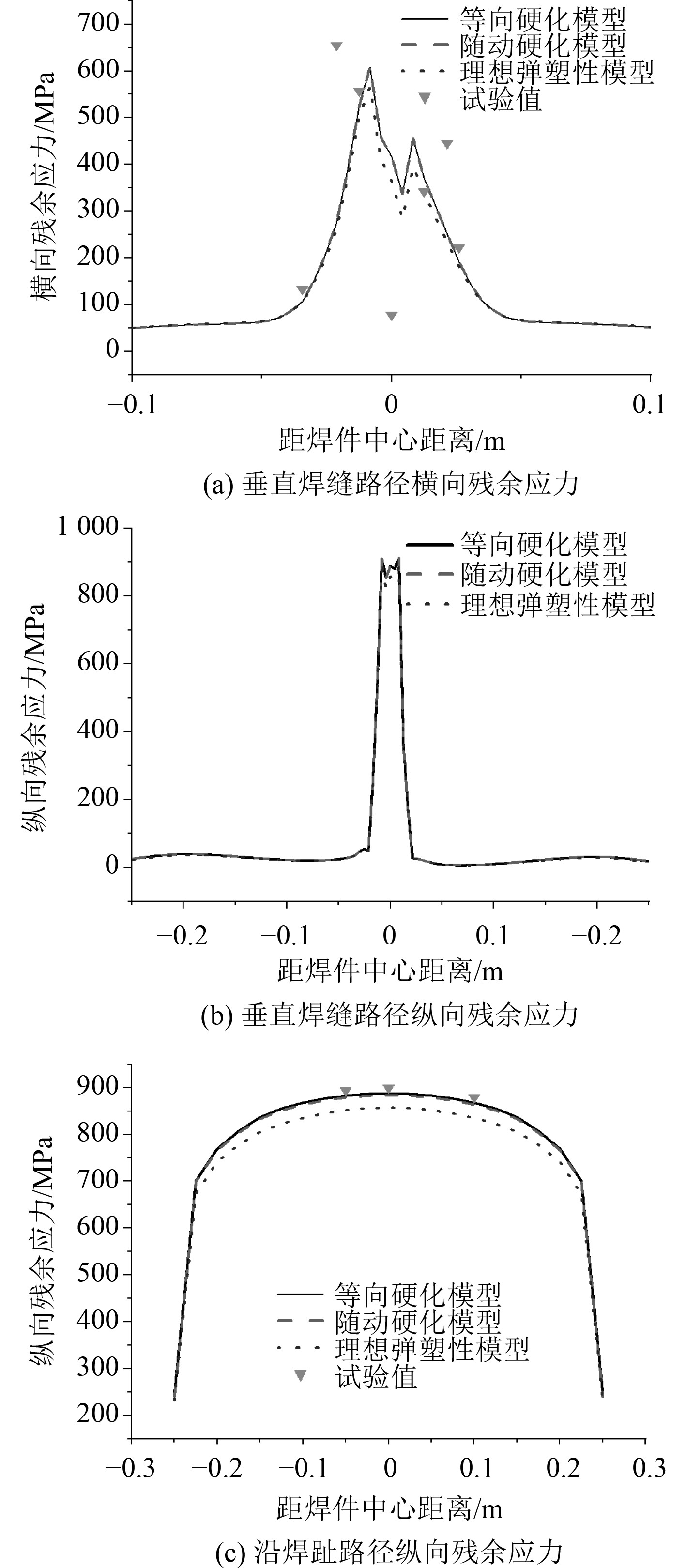
图9分别为Ti80对接焊平板垂直焊缝路径、沿焊趾路径的横向和纵向残余应力和试验结果对比。
|
图 9 不同硬化模型的焊接残余应力 Fig. 9 Welding residual stress distribution of different hardening models |
1)由图9(a)可知,垂直焊缝路径的横向残余应力表现为拉应力;横向残余应力最大值约为630 MPa,等向硬化模型和随动硬化模型的残余应力结果较大。
2)由图9(b)可知,纵向残余应力最大值约为910 MPa,超过了材料的屈服强度,且纵向残余应力最大值大于横向残余应力,等向硬化模型和随动硬化模型的残余应力结果较大。
3)由图9(c)可知,沿焊趾路径上纵向残余应力均表现为拉应力,纵向残余应力最大值约为890 MPa。
总体来说,硬化模型对Ti80对接焊平板模型残余应力影响较小。等向模型和随动硬化模型的焊接残余应力结果更加接近文献试验结果。
4 结 语本文采用数值模拟方法对材料硬化模型对钢材和钛合金对接焊平板模型残余应力的影响进行研究,得到如下结论:
1)采用等向硬化模型计算分析的SUS304不锈钢和屈服强度为918 MPa高强度钢对接焊平板模型的残余应力结果较大,与文献试验结果更加符合;随动硬化模型和理想弹塑性模型的残余应力结果偏小;硬化模型对这2种材料的对接焊平板模型纵向残余应力影响更加明显。
2)等向模型下的Q345钢对接焊平板的焊接残余应力结果最大,而随动硬化模型和理想弹塑性模型结果偏小;硬化模型对纵向焊接残余应力的影响更加明显。
3)硬化模型对Ti80对接焊平板残余应力的影响不明显,数值模拟结果与试验结果接近。
总体来说,硬化模型对SUS304不锈钢、屈服强度为918 MPa的高强度钢和Q345钢这3种钢材的对接焊平板模型的纵向残余应力影响更加明显,对横向残余应力的影响较小;而硬化模型对Ti80对接焊平板模型的残余应力影响不大。
| [1] |
LEMAITRE J, JEAN-LOUIS C. Mechanics of Solid Materials[M]. Cambridge University Press, 1990.
|
| [2] |
JEAN-LOUIS C. A review of some plasticity and viscoplasticity constitutive theories[J]. International Journal of Plasticity, 2008, 24(10): 1642-1693. DOI:10.1016/j.ijplas.2008.03.009 |
| [3] |
MICHAEL C S, RENÉ V M, MURÁNSKY O, et al.. Comprehensive numerical analysis of a three-pass bead-in-slot weld and its critical validation using neutron and synchrotron diffraction residual stress measurements[J]. International Journal of Solids and Structures, 2012, 49(9): 1045-1062. DOI:10.1016/j.ijsolstr.2011.07.006 |
| [4] |
MICHAEL C S, ROGER J D, JOHN B, et al.. Accurate prediction of residual stress in stainless steel welds[J]. Computational Materials Science, 2012, 54: 312-328. DOI:10.1016/j.commatsci.2011.10.024 |
| [5] |
MURANSKY O, CORY H, VIPULKUMAR I P, et al. The influence of constitutive material models on accumulated plastic strain in finite element weld analyses[J]. International Journal of Solids and Structures, 2015, 69/70: 518-530. DOI:10.1016/j.ijsolstr.2015.04.032 |
| [6] |
XU Jijin, PHILIPPE G, et al. Temperature and residual stress simulations of the NeT single-bead-on-plate specimen using SYSWELD[J]. International Journal of Pressure Vessels and Piping, 2012, 99-100. DOI:10.1016/j.ijpvp.2012.08.002 |
| [7] |
MICHAEL C S, ANN C S. NeT bead-on-plate round robin: Comparison of residual stress predictions and measurements[J]. International Journal of Pressure Vessels and Piping, 2008, 86(1). DOI:10.1016/j.ijpvp.2008.11.017 |
| [8] |
JIAMIN S, JONAS H, JAKOB K, et al. Solid-state phase transformation and strain hardening on the residual stresses in S355 steel weldments[J]. Journal of Materials Processing Technology, 2019, 265: 173-184. DOI:10.1016/j.jmatprotec.2018.10.018 |
| [9] |
DENG D, ZHANG Chaohua, PU Xiaowei, et al. Influence of material model on prediction accuracy of welding residual stress in an austenitic stainless steel multi-pass butt-welded joint[J]. Journal of Materials Engineering and Performance, 2017, 26(4): 1494-1505. DOI:10.1007/s11665-017-2626-6 |
| [10] |
戴德平. 奥氏体不锈钢焊接接头残余应力的数值模拟研究[D]. 重庆: 重庆大学, 2016.
|
| [11] |
WANG Qiang, LIU Xuesong, WANG Ping, et al. Numerical simulation of residual stress in 10Ni5CrMoV steel weldments[J]. Journal of Materials Processing Technology, 2017, 240: 77-86. DOI:10.1016/j.jmatprotec.2016.09.011 |
| [12] |
耿鲁阳, 涂善东, 巩建鸣, 等. 不同材料硬化模型模拟13MnNiMoR钢超厚圆筒对接环焊接残余应力[J]. 机械工程材料, 2019, 43(3): 60-66. DOI:10.11973/jxgccl201903012 |
| [13] |
刘瑞堂, 刘文博, 刘锦云. 工程材料力学性能[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001.
|
| [14] |
卓家寿, 黄丹. 工程材料的本构演绎[M]. 北京: 科学出版社, 2009: 58-86.
|
| [15] |
LI Liangbi, JIA Qianqian, WAN Zhengquan, et al. Experimental and numerical investigation of effects of residual stress and its release on fatigue strength of typical FPSO-unit welded joint[J]. Ocean Engineering, 2020, 196: 106858. DOI:10.1016/j.oceaneng.2019.106858 |
| [16] |
拉达伊. 焊接热效应: 温度场﹑残余应力﹑变形[M]. 北京: 机械工业出版社, 1997.
|
| [17] |
CARLOS G. Matos, Robert Dodds. Modeling the effects of residual stresses on defects in welds of steel frame connections[J]. Engineering Structures, 2000, 22(9): 1103-1120. DOI:10.1016/S0141-0296(99)00055-3 |
| [18] |
陈家权, 沈炜良, 尹志新, 等. 基于单元生死的焊接温度场模拟计算[J]. 热加工工艺, 2005(7): 64-65. DOI:10.14158/j.cnki.1001-3814.2005.07.026 |
| [19] |
LIU Chuan, LUO Ying, YANG Min, et al. Effects of material hardening model and lumped-pass method on welding residual stress simulation of J-groove weld in nuclear RPV[J]. Engineering Computations (Swansea, Wales), 2016, 33(5): 1435-1450. DOI:10.1108/EC-08-2015-0216 |
| [20] |
LIU Chuan, LUO Ying, YANG Min, et al. Three-dimensional finite element simulation of welding residual stress in RPV with two J-groove welds[J]. Welding in the World, 2017, 61(1): 151-160. DOI:10.1007/s40194-016-0392-y |
| [21] |
李万润, 张广隶, 刘宇飞, 等. Q345B钢梁柱节点焊接残余应力模拟及试验验证[J]. 华南理工大学学报(自然科学版), 2019, 47(10): 114-123. DOI:10.12141/j.issn.1000-565X.190044 |
| [22] |
孙凯翔. 深海载人潜水器耐压球壳赤道焊接残余应力研究[D]. 镇江: 江苏科技大学, 2020.
|
 2022, Vol. 44
2022, Vol. 44

