2. 北京大学南昌创新研究院,江西 南昌 330096;
3. 中国船舶集团有限公司第七〇五研究所昆明分部,云南 昆明 650101
2. Nanchang Innovation Institute of Peking University, Nanchang 330096, China;
3. Kunming Branch of the 705 Research Institute of CSSC, Kunming 650101, China
水下航行器是实施水下勘探、运输、侦察、作战等活动的重要载体,在海洋科学及国防军事等领域具有重要应用价值。水下航行器行进时受到的阻力限制了航行速度,其带来的能量消耗不仅制约了航程,也限制了负载能力,对水下航行器的快速性产生严重影响[1-2]。水下航行器在航行过程中一般需要克服2种阻力:1)压差阻力,即水下航行器头部和尾部之间的压力差所形成的阻力,与航行器的外形设计有关;2)摩擦阻力,即航行器与周围水流摩擦而形成的阻力,与航行器表面的结构形貌、浸润特性等有关。水流场中近壁面摩擦阻力占到总阻力的比例可以高达70%[3]。因此,近壁面摩擦阻力是影响水下航行器速度和能耗的关键,是水动力学、船舶工程等领域关注的重要问题。
本文立足于水下滑移边界减阻技术,重点论述水下滑移边界的基本理论、实现形式,以及气-液界面和液体浸润表面减阻的研究进展,探讨水下滑移边界减阻研究中存在的关键科学问题,并对水下航行器减阻技术的未来发展趋势进行展望,为水下航行器减阻性能优化提供参考借鉴。
1 滑移边界条件 1.1 理论模型对于完全浸润的固-液表面,一般认为固-液界面处的速度为0,即无滑移边界条件,如图1(a)所示。相比之下,气-液界面或者液体浸润表面导致流体不再与固体直接接触,而是与气体或者润滑液体接触,形成滑移边界条件,如图1(b)所示,其中,Fluid 1为外部连续运动的流体,Fluid 2为固体表面微结构中的浸润流体(气体或润滑液体)。水下固体微结构表面的优良减阻特性源于滑移边界条件,滑移边界条件使得水下固体结构表面附近流体的流动性增强,同时还具有减阻、防粘附、防结冰、防腐蚀的潜力[4]。

|
图 1 边界条件 Fig. 1 Boundary conditions |
早在1823年,Navier提出了滑移边界条件的概念[5]。在Navier滑移模型中,滑移速度(us)正比于壁面处的速度剪切率为:
| $ {u_s} = b{\left. {\frac{{\partial u}}{{\partial y}}} \right|_{wall}}。$ | (1) |
式中:b是滑移长度,
当具有疏水性质的固体微结构表面浸润在水下时,气层被钉扎在固体微结构表面的顶部,因此,在流体和浸没的固体微结构之间会形成气-液界面[4]。对于气-液界面,由于气体的粘度比水的粘度低98%,所以气-液界面在理论可以被认为是无剪切的滑移表面[7],导致其可以实现很大的减阻。
气-液界面在复杂流动下的形态演化和稳定性是评估滑移边界能否实现的必要因素,对于其工程应用是非常重要的。目前关于气-液界面形态演化和稳定性的理论一般分为2类,分别是从力学平衡和能量角度考虑的。Emami等[8]和Piao等[9]从液-气界面力学平衡的角度出发,分别给出了界面在静水和流动状态下失稳的判据;吕鹏宇等[10]从能量角度出发,建立了界面的热力学自由能模型,研究了不同压强和溶解度影响下的气层稳定性,预测了长时间稳定状态的存在,并通过实验得以证实。结果表明,在高静水压和流动剪切作用下,气-液界面会失稳,导致减阻性能消失。然而,目前的研究局限于简单流动环境和简单固体结构,针对复杂流动条件下,复杂固体表面构型的气-液界面稳定性理论还不完善。因此,进一步研究复杂流动条件下复杂微结构表面的稳定性,实现稳定的滑移边界条件是亟待解决的科学问题。
1.2.2 液体浸润表面受猪笼草的启发,当水下固体表面微结构内部的气体被与水互不相容的润滑液体替代之后会形成液体浸润表面。与气-液界面类似,液体浸润表面也可以在界面处形成滑移边界条件,增强界面外液体的流动性能,实现减阻[11]。此外,液体浸润表面还具有自清洁、防污、自修复、抵抗各种液体、定向收集水和与摩擦纳米发电机(Teng)结合发电等工程应用价值[12]。
液体浸润表面的减阻特性也源于其滑移特性。但是,与气-液界面不同的是,液体浸润表面中润滑液体具有不可压缩的特性,可以很好地克服气-液界面存在的高静水压失稳问题[13]。润滑液体具有一定的粘性,粘度记为μi,界面外连续流体的粘度为μo,则粘度比为N=μo/μi。研究表明,界面两侧的流体属性(粘度比N)会影响液体浸润表面的稳定性,进而影响减阻率[14]。虽然液体浸润表面能够承受较高的静水压,但是面对流动剪切环境,微结构中的润滑油会被剪切走,导致减阻效果下降,相关研究还处于初步探索阶段。
2 气-液界面的减阻机理 2.1 层流减阻机理经过几十年的研究,研究者已经从理论分析、数值模拟、实验测量等不同角度证实了层流状态下水下气-液界面的减阻机理,即气-液界面的减阻率(DR)主要由滑移长度(b)决定,即DR=f(b)。而气-液界面分数(GF)对气-液界面的滑移长度有较大的影响,因此,水下固体微结构表面的流动减阻性能主要依赖于所维持的气-液界面的比例[15]。
从理论分析的角度,研究人员分析出减阻率与滑移长度的关系。2006年,Choi等[16]针对Couette流,提出了减阻率和滑移长度的表达式:DR=1/(1+H/b)。其中,H表示滑移表面和无滑移表面之间的距离,b表示滑移长度。针对Poiseuille 流动,Qu等[17]提出了一个类似的表达式:DR=3/(3+H/b)。因此,在层流状态下,减阻率和滑移长度直接相关。
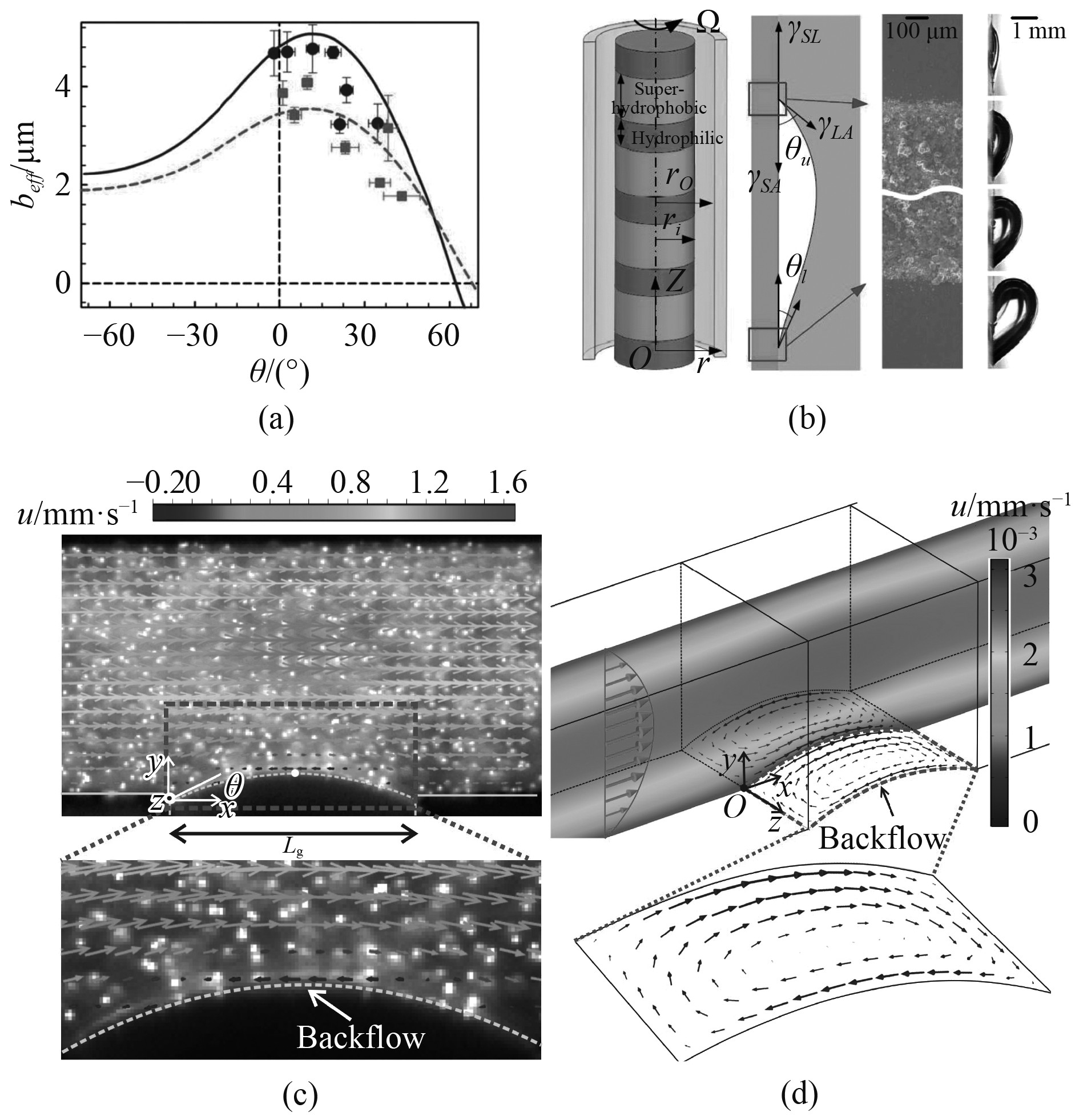
从数值模拟的角度,研究人员分析了减阻率和滑移长度之间的关系。Karatay[6]通过Comsol软件研究了气-液界面突出角度对减阻率的影响,结果表明,气-液界面的减阻率和滑移长度均随气-液界面的突出角度先增加后减小(图(2a)),最大减阻率为23%,对应的滑移长度也为最大值。Park等[18]通过DNS研究了不同雷诺数情况下气-液界面减阻率的变化规律,结果表明,在层流状态下,减阻率和滑移长度均不随雷诺数变化,且最大减阻率为40%,对应的滑移长度也为最大值。
|
图 2 层流减阻研究现状 Fig. 2 Laminar drag reduction |
从实验的角度,研究人员通过流变仪、Taylor-Couette、micro-PIV、压降测量等滑移长度测量方法,对层流状态下滑移边界的减阻率进行了研究。Hu等[19]在Taylor-Couette实验中对环形的疏水表面进行减阻测试,得到的最大减阻率为77.2% (见图2b)。Song等[20]通过micro-PIV实验,研究了微流道中流向沟槽气-液界面的减阻率,实验观察到的最大减阻率仅仅为1.2%。Peaudecerf等[21]通过micro-PIV实验也发现,实验测量得到的气-液界面的滑移长度远小于理论预测。
尽管理论和数值模拟预测出在层流状态下气-液界面可能具有较大的滑移长度和减阻效果,但是在micro-PIV实验中发现滑移长度的测量值与理论预测值依然存在显著的差异,这是因为流体中的表面活性剂对滑移长度和减阻率的影响一直被忽略,直到Peaudecerf等[21]的研究表明,连续流体中的溶解物(表面活性剂)会大大降低气-液界面的滑移性能和减阻效果。进一步地,Li等[22]通过micro-PIV实验发现,在三维流动下,活性剂甚至会导致气-液界面附近产生回流现象(见图2(c)和图2(d))。揭示了三维回流的产生机制,主要是由于展向和流向的表面张力梯度共同导致,还评估了活性剂对滑移特性和减阻效果的影响。
2.2 湍流减阻机理与层流不同,在湍流状态下,气-液界面的减阻机理尚不清楚。但是可以推断的是,湍流减阻是由气-液界面有效滑移长度和近壁流动结构共同影响的。研究人员已经对湍流状态下气-液界面的减阻机理进行了一定的研究,但并未达到共识。
2006年,研究人员开始试图预测湍流中气-液界面减阻率的理论表达式。Fukagata等[23]推导了槽道湍流中减阻率与流向和展向滑移长度之间的理论关系式。Min等[24]采用直接数值模拟方法,通过给定无量纲的滑移长度,研究了气-液界面在槽道湍流中的减阻率。结果表明,滑移长度越大,减阻率越大,最大减阻率为29%。2013年,Park等[18]也采用直接数值模拟方法,将气-液界面的边界条件设置为无剪切,研究了气-液界面在槽道湍流中的减阻率。结果表明,随着GF增加,无量纲滑移长度增加,减阻率也增加,最大减阻率为90%。
然而,在已有的文献中,关于气-液表面湍流状态下的减阻率并不一致,对减阻机理的认识也不清楚。研究者通过实验测量得到的减阻率从0%,11%到最高80%[25]都有报道。这是因为与层流实验对比,湍流实验的测量增加了许多挑战。1)湍流状态下较大的压力波动会降低气-液界面的稳定性,流动切应力会破坏固体表面的物理结构,导致转变;2)由于实验中有限的空间分辨率和气-液界面的反射,传统PIV方法测量近壁(粘性子层区域)速度场的难度增大[26]。因此,受上述挑战的限制,只有很少的几个实验研究了湍流状态下气-液界面的滑移速度或者滑移长度对DR的影响。2016年,Ling等[27]使用数字全息PIV的方法在湍流边界层流动中测量了气-液界面附近(y+<5)的滑移速度,实验结果表明,在平均速度为2.0 m/s时,最大减阻率为36%。
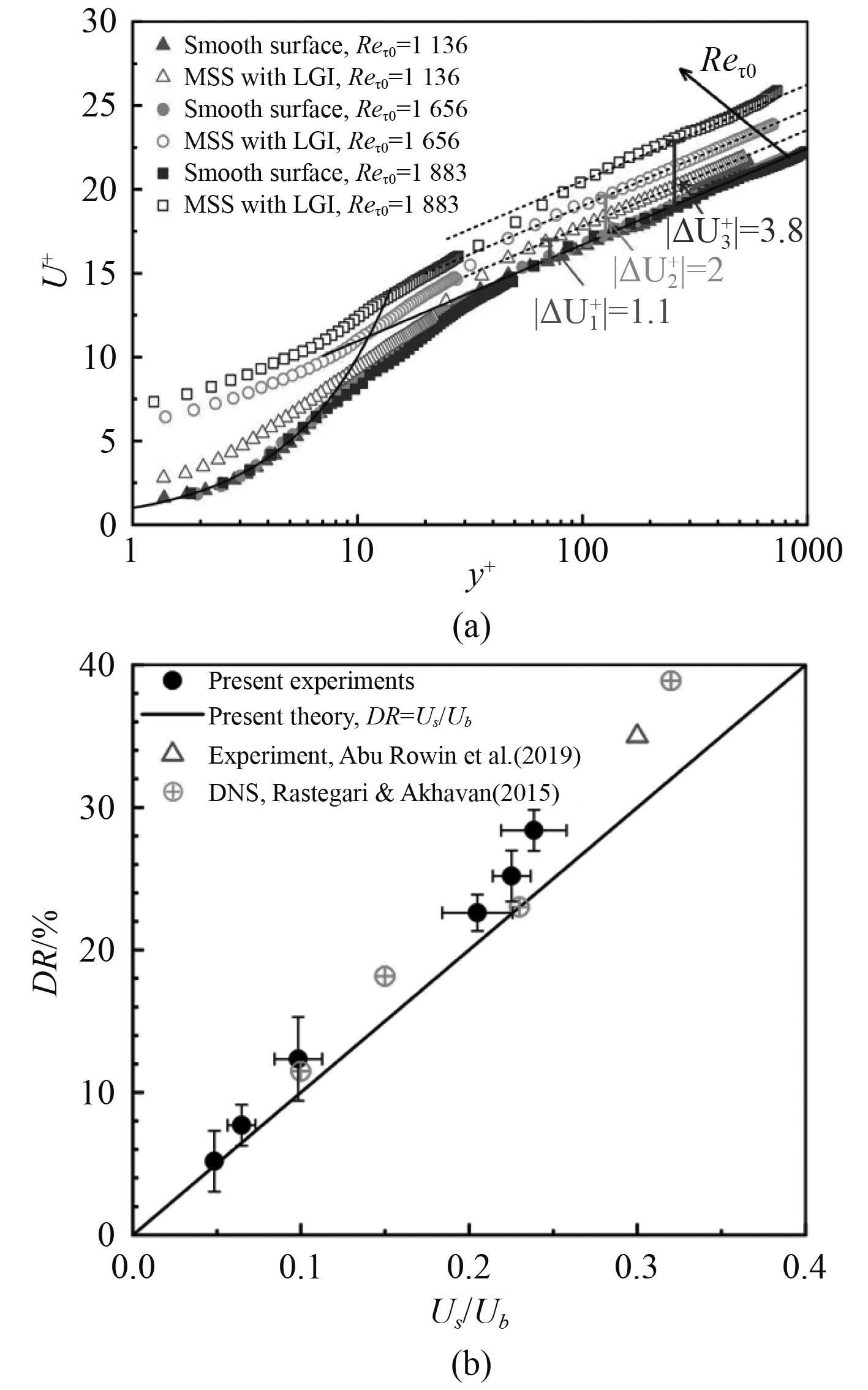
尽管最近的实验研究已经报道了在湍流状态下使用气-液界面可以获得一定的减阻,但是,实验测量得到的DR与滑移长度、近壁面湍流结构的关系并不清楚。Li等[28]搭建了重力式湍流循环水洞,开发了近壁PIV算法,直接测量了气-液界面在不同摩擦雷诺数下的近壁速度剖面并计算了流动剪切力,实验发现减阻率随着摩擦雷诺数的增加而增加,如图3所示。通过理论与实验结果对比,揭示了雷诺数对气-液界面湍流减阻的影响机理:减阻率随雷诺数增加主要是由于气-液界面的滑移特性随着雷诺数增加导致。
|
图 3 雷诺数对气-液界面速度和减阻率的影响[28] Fig. 3 Effect of Reynolds number on velocity and drag reduction at liquid-gas interface |
近20年来,研究人员已经对气-液界面的减阻机理有了一定的认识。但是,直到最近几年才有研究者证实液体浸润表面在层流和湍流中能够减阻。2014年,Solomon等[29]通过平板流变仪实验测量得到液体浸润表面的最大减阻率为16%,对应的滑移长度为18 μm。Rosenberg等[30]首次通过Taylor-Couette实验证明了湍流状态下,液体浸润表面可以实现减阻。同时对比了高流速下气-液界面和液体浸润表面的减阻率。在所测试的雷诺数范围内,气-液界面的减阻率约为10%,而液体浸润表面减阻率约为14%,这是因为高速剪切下液体浸润表面的界面稳定性更好。除了实验测量之外,研究者还通过数值模拟对液体浸润表面的减阻率进行了预测。2017年,Buren等[31]通过直接数值模拟同时预测了湍流状态下,气-液界面和液体浸润表面在Taylor-Couette流动中的减阻效果,数值计算结果表明,气-液界面可实现的最大减阻率为35%,液体浸润表面可以实现的最大减阻率为45%。Fu等[32]也通过直接数值模拟方法研究了湍流状态下液体浸润表面的减阻率随粘度比和滑移长度的变化规律,实现的最大减阻率约为78%。
综上所述,研究人员目前主要采用数值模拟和实验测量的方法研究液体浸润表面的减阻机理,然而实验研究主要集中在Taylor-Couette流动,对于其他流动形式下(比如,槽道流、湍流边界层流动)液体浸润表面的减阻机理还缺乏系统的研究。这是因为液体浸润表面减阻实验研究具有许多挑战:1)高速流动剪切会导致液体浸润表面上的液-液界面失稳,导致减阻测量结果随机误差较大;2)较大的压力脉动会导致界面形貌发生变化,导致实验过程中难以精准捕捉其位置。因此,需要对液体浸润表面附近开展更精细的流场精细测量,并结合理论和数值模拟来揭示其减阻机理。
4 滑移边界减阻技术的工程应用到目前为止,受限于滑移表面大面积制备技术和减阻率测试方法,现有滑移边界减阻技术大部分应用于有限大小的表面,并在实验室开展实验,而将滑移减阻技术应用到整个水下航行器上并在湖上或海上进行减阻实验研究的文献屈指可数。
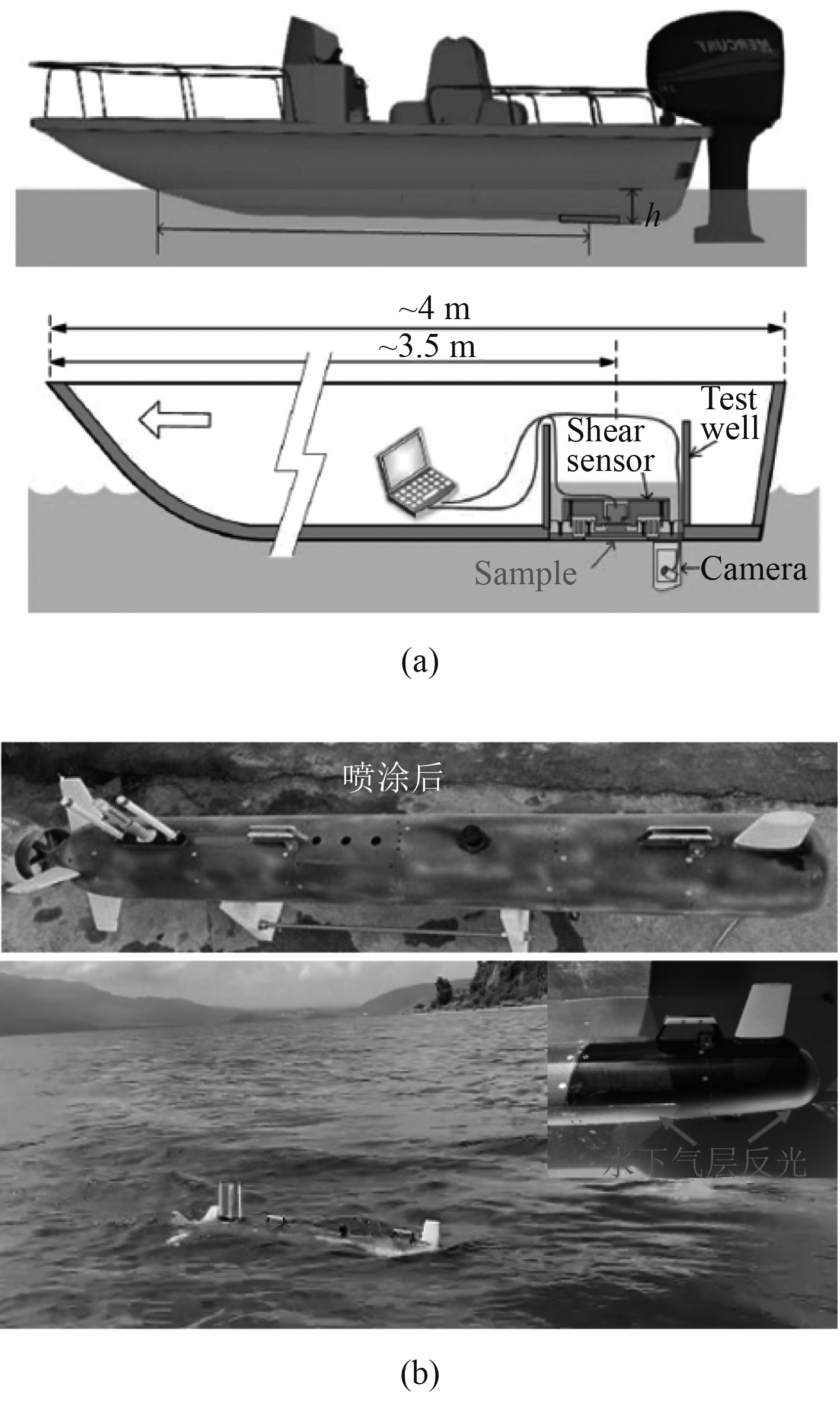
Zhang等[33]开展了潜艇模型在层流状态下的减阻实验,模型的尺寸为3.5 cm×3.7 cm×33.0 cm。通过将疏水性铜颗粒固定在预交联的聚二甲基硅氧烷(PDMS)表面上,实现在潜艇模型表面上大面积制备超疏水涂层。实验过程中,保证相同的功率和实验条件,分别测试亲水和疏水模型,疏水模型减阻率达到15%。2018年,Reholon等[34]研究了在湍流状态下总长度为508 mm的自主水下航行器(AUV)模型的减阻特性,测试的雷诺数范围是5.0×105~1.2×106,当雷诺数为5.0×105时测量得到的最大减阻率为36%,这与其他文献中减阻的规律不同,对滑移边界减阻技术的工程应用又提出了新的挑战。2020年,Xu等[35]在开放水域对摩托艇下方的船体表面进行阻力测试,基于微梁测力系统测得的最大减阻约为30%,测试的样品大小为40 mm×70 mm,对应的航速约为5.14 m/s(见图4(a))。北京大学段慧玲团队结合水下装备减阻的需求,将滑移边界减阻技术应用到水下航行器上,有效提升了该型水下装备的航程与航速,满足了新型装备对快速性的需求,如图4(b)所示。
|
图 4 海洋装备减阻测试 Fig. 4 Drag reduction test with marine equipments. |
目前,对水下航行器等装备减阻技术的研究已经不再局限于传统水动力学领域,而是与流体力学、固体力学、仿生学、智能材料、协同控制、流固耦合力学等各学科交叉,朝着减阻率更高、隐蔽性更强、综合性能更优的方向发展。未来,在深入研究超强动力推进器、超长续航电池、低阻力型线的基础上,进一步考虑表面微结构形貌、等效滑移边界等表界面科学与技术的应用,将为研发出新一代高效减阻技术提供重要的支撑。
| [1] |
RASHIDI S, HAYATDAVOODI M, ESFAHANI J A, Vortex shedding suppression and wake control: A review [J]. Ocean Engineering, 2016, 126: 57–80.
|
| [2] |
冯景祥, 姚尧, 潘峰, 等. 国外水下无人装备研究现状及发展趋势[J]. 舰船科学技术, 2021, 43(23): 1-8. |
| [3] |
FUKUDA K, TOKUNAGA J, NOBUNAGA T, et al. Frictional drag reduction with air lubricant over a super-water-repellent surface[J]. Journal of Marine Science & Technology, 2000, 5(3): 123-130. |
| [4] |
XUE Y H, LV P Y, LIN H, et al. Underwater superhydrophobicity: Stability, design and regulation, and applications[J]. Applied Mechanics Reviews, 2016, 68(3): 30803. DOI:10.1115/1.4033706 |
| [5] |
ROTHSTEIN J P. Slip on Superhydrophobic Surfaces[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 89-109. DOI:10.1146/annurev-fluid-121108-145558 |
| [6] |
KARATAY E, HAASE A S, VISSER C W, et al. Control of slippage with tunable bubble mattresses[J]. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(21): 8422-8426. DOI:10.1073/pnas.1304403110 |
| [7] |
LI D D, LI S C, XUE Y H, et al. The effect of slip distribution on flow past a circular cylinder[J]. Journal of Fluids and Structures, 2014, 51: 211-224. DOI:10.1016/j.jfluidstructs.2014.07.017 |
| [8] |
EMAMI B, TAFRESHI H V, GAD-EL-HAK M, et al. Effect of fiber orientation on shape and stability of air–water interface on submerged superhydrophobic electrospun thin coatings[J]. Journal of Applied Physics, 2012, 111(6): 64325. DOI:10.1063/1.3697895 |
| [9] |
PIAO L, PARK H. Two-dimensional analysis of air-water interface on superhydrophobic grooves under fluctuating water pressure[J]. Langmuir, 2015, 31(29): 8022-8032. DOI:10.1021/acs.langmuir.5b01847 |
| [10] |
吕鹏宇, 薛亚辉, 段慧玲. 超疏水材料表面液-气界面的稳定性及演化规律[J]. 力学进展, 2016, 46(1): 179-225. |
| [11] |
WONG T S, KANG S H, TANG S, et al. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity[J]. Nature, 2011, 477(7365): 443-447. DOI:10.1038/nature10447 |
| [12] |
FU M K, ARENAS I, LEONARDI S, et al. Liquid-infused surfaces as a passive method of turbulent drag reduction[J]. Journal of Fluid Mechanics, 2017, 824: 688-700. DOI:10.1017/jfm.2017.360 |
| [13] |
YAN X T, JIN Y K, CHEN X M, et al. Nature-inspired surface topography: design and function[J]. Science China Physics, Mechanics & Astronomy, 2019, 63(2): 224601. |
| [14] |
LIU Y, WEXLER J S, SCHÖNECKER C, et al. Effect of viscosity ratio on the shear-driven failure of liquid-infused surfaces[J]. Physical Review Fluids, 2016, 1(7): 74003. DOI:10.1103/PhysRevFluids.1.074003 |
| [15] |
文俊, 胡海豹, 杜鹏, 等. 超疏水表面水下减阻研究[C]//第二十九届全国水动力学研讨会, 2018.
|
| [16] |
CHOI C H, KIM C J. Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface[J]. Physical Review Letters, 2006, 96(6): 66001. DOI:10.1103/PhysRevLett.96.066001 |
| [17] |
OU J, PEROT B, ROTHSTEIN J P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces[J]. Physics of Fluids, 2004, 16(12): 4635-4643. DOI:10.1063/1.1812011 |
| [18] |
PARK H, PARK H, KIM J. A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow[J]. Physics of Fluids, 2013, 25(11): 110815. DOI:10.1063/1.4819144 |
| [19] |
HU H, WEN J, BAO L, et al. Significant and stable drag reduction with air rings confined by alternated superhydrophobic and hydrophilic strips[J]. Science Advances, 2017, 3(9): 1603288.
|
| [20] |
DONG S, SONG B, HU H, et al. Effect of a surface tension gradient on the slip flow along a superhydrophobic air-water interface[J]. Physical Review Fluids, 2018, 3(3).
|
| [21] |
PEAUDECERF F J, LANDEL J R, GOLDSTEIN R E, et al. Traces of surfactants can severely limit the drag reduction of superhydrophobic surfaces[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(28): 7254-7259. DOI:10.1073/pnas.1702469114 |
| [22] |
LI H, LI Z, TAN X, et al. Three-dimensional backflow at liquid–gas interface induced by surfactant[J]. Journal of Fluid Mechanics, 2020, 899. |
| [23] |
FUKAGATA K, KASAGI N, KOUMOUTSAKOS P. A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces[J]. Physics of Fluids, 2006, 18(5): 360. |
| [24] |
TAEGEE M, JOHN K. Effects of hydrophobic surface on skin-friction drag[J]. Physics of Fluids, 2004, 16(7): 55-58. DOI:10.1063/1.1755723 |
| [25] |
GOSE J W, GOLOVIN K, BOBAN M, et al. Characterization of superhydrophobic surfaces for drag reduction in turbulent flow[J]. Journal of Fluid Mechanics, 2018, 845: 560-580. DOI:10.1017/jfm.2018.210 |
| [26] |
ZHANG J, TIAN H, YAO Z, et al. Mechanisms of drag reduction of superhydrophobic surfaces in a turbulent boundary layer flow[J]. Experiments in Fluids, 2015, 56(9).
|
| [27] |
LING H, SRINIVASAN S, GOLOVIN K, et al. High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces[J]. Journal of Fluid Mechanics, 2016, 801: 670-703. DOI:10.1017/jfm.2016.450 |
| [28] |
LI H, JI S, TAN X, et al. Effect of Reynolds number on drag reduction in turbulent boundary layer flow over liquid–gas interface[J] Physics of Fluids, 2020, 32: 122111.
|
| [29] |
SOLOMON B R, KHALIL K S, VARANASI K K. Drag reduction using lubricant-impregnated surfaces in viscous laminar flow[J]. Langmuir, 2014, 30(36): 10970. DOI:10.1021/la5021143 |
| [30] |
ROSENBERG B J, BUREN T V, FU M K, et al. Turbulent drag reduction over air and liquid impregnated surfaces [J]. Physics of Fluids, 2016, 28(1).
|
| [31] |
VAN BUREN T, SMITS A J. Substantial drag reduction in turbulent flow using liquid-infused surfaces[J]. Journal of Fluid Mechanics, 2017, 827: 448-456. DOI:10.1017/jfm.2017.503 |
| [32] |
FU M K, ARENAS I, LEONARDI S, et al. Liquid-infused surfaces as a passive method of turbulent drag reduction[J]. Journal of Fluid Mechanics, 2017, 824: 688−700.
|
| [33] |
ZHANG S, OUYANG X, Li J, et al. Underwater drag-reducing effect of superhydrophobic submarine model[J]. Langmuir, 2015. 31(1): 587.
|
| [34] |
REHOLON D, GHAEMI S. Plastron morphology and drag of a superhydrophobic surface in turbulent regime[J]. Physical Review Fluids, 2018, 3(10).
|
| [35] |
XU M, GRABOWSKI A, YU N, et al. Superhydrophobic drag reduction for turbulent flows in open water[J]. Physical Review Applied, 2020, 13(3).
|
 2022, Vol. 44
2022, Vol. 44
