0 引　言

随着电子商业快速发展，容积率大、时效性强的多载具自动化存取系统正在成为物资存储的主要形式，整齐优化的货位摆放是该存取系统高效出库的前提，自动化存取系统优化问题是目前物资仓储领域的研究热点之一。文献[1]已将仓储货位分配问题归纳为广义的布局问题，其复杂性等价于NP完全问题。

文献[2-7]从优化同组货品距离、最小化作业时间、货架重心等方面建模，使用改进遗传算法优化货架存储结构；文献[8]参考货架重心、物资选用频率、货物出入时间等因素建立货位分配模型，使用优化的差分进化算法优化货位分配；文献[9]考虑了货架的稳定性和出入库效率等因素，建立了自动化存取系统货位优化的数学模型，提出了改进粒子群算法来解决该问题。

上述研究多采用遗传、粒子群等优化类算法求解。其中，遗传算法基于概率规则，具有搜索灵活、全局搜索能力强的优点，但易过早收敛陷入局部最优解；粒子群算法局部搜索能力强，但收敛速度慢。考虑到本系统对货位优化效率的要求，将结合蒙特卡罗树搜索（Monte Carlo tree search，MCTS）算法进行货位优化求解，该方法通过提前预测输入优化步骤在模拟运行的输出值，不断以模型优化为目标学习货位优化运行策略，通过快速模拟试错实现该自动化存取系统货位优化分配。

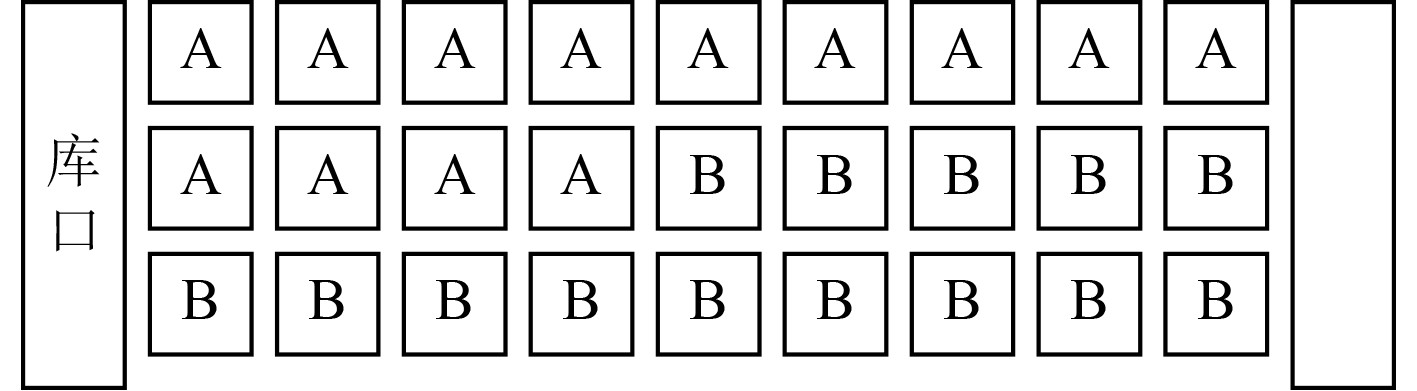
1 问题描述及建模 1.1 问题描述

以某型多载具自动化存取系统为研究对象，该系统包含3层理货通道（位于仓库中间）和2个垂直通道，出口在仓库前方，货物统一由出口出库。该自动化存取系统初始为同类聚集排列状态，如图1所示。在日常运行过程中，调度员按需控制货箱进行出入库操作，使用中有可能会将一箱物资全部使用，有可能只使用其中一部分。物资出库完成后，将货箱回库。形成的状态之一如图2所示。图中“空”代表空箱，“半A”代表半箱A类型物资，“半B”以此类推。入库及使用过程中A（代表整箱A，同理于B）、B、半箱A、半箱B、空箱出现库存乱序现象。

该状态下，再执行某型货箱的出库操作，如图2中需要A类物资出库，此时需进行3轮循环操作，将A循环至库口才能出库，这将导致拣货员等待时间过长（每轮循环需对2行所有货箱移动一位），出库效率大幅度降低，同时可能导致自动化存取系统的库房载荷不均衡等问题。

1.2 模型建立

根据文献[10]货位分配中的选择自动货箱进行库存调整的过程可以被视为马尔科夫决策过程（Markov decision process, MDP），因此，自动化存取系统内货位优化可采用马尔科夫决策通过4元组{S，A，P，R}进行建模。其中，S表示自动化存取系统货位状态空间，A表示仓库机构当前可执行的动作空间，R表示货位移动后可获得的奖励函数，P表示根据仓库现有节点树进行的剪枝优化操作。

1）状态空间

状态空间中的每一个状态S都是一个三维特征向量，如第i阶段状态Si=（Vi，Ai-1，Mi），其中Vi代表第i阶段初累计货位优化动作，Ai-1代表第i-1阶段选择的计划货位优化动作，Mi代表第i阶段对应的时间信息。如此来描述状态是因为在货位形式确定的情况下，Vi可以反映第i阶段的货位状态，Ai-1的设定可以约束第i阶段的货位优化工程量，Mi可以反映当前步骤对应的货位优化搬运量时间量化因子，以表示货位优化动作对时间的影响。

2）动作空间

货位优化过程中，算法根据当前库存状态选择货箱运行动作，货箱运行的目的是将同类型分布于自动化存取系统各层的同类型货箱进行合并。多载具自动化存取系统按照指令周期模式进行运作，通过平移装置、货箱升降平台的配合完成各指令操作。自动化基本动作集合见表1。其中， $\left[ {{x_{{K_{ij\left( {t - 1} \right)}}}},{y_{{K_{ij\left( {t - 1} \right)}}}}} \right]$ 表示第Ki类型货箱的第j个货箱的当前坐标， $\left[ {{x_{{K_{ijt}}}},{y_{{K_{ijt}}}}} \right]$ 为货箱移动后坐标； ${\eta _1}$ 和 ${\eta _2}$ 分别为平移、纵移时间参数。

3）奖励函数

在货位优化马尔科夫模型中，奖励函数主要包含收益计算、整体奖励得分。收益计算包括对库存的聚合度、货位优化时间当前状态与之前状态的对比，其中货位聚合度是指自动化存取系统内同类型货箱坐标集中程度。

计算货位聚合度。首先，定义第t次货位优化后第K_i类货箱的平均坐标：

$ \overline {{c_{t{K_i}}}} \left[ {x,y} \right] = \frac{1}{{{K_i}}}\mathop \sum \limits_{j = 1}^{{K_{in}}} \left[ {{x_{t{K_{ij}}}},{y_{t{K_{ij}}}}} \right] 。$

(1)

其中， $\overline {{c_{t{K_i}}}} \left[ {x,y} \right]$ 表示第t次货物优化时第K_i类货箱的坐标均值，j表示第K_i类型货箱的第j个货箱， $[ {x_{t{K_{ij}}}}, $ $ {y_{t{K_{ij}}}} ]$ 表示第K_i类型货箱的第j个货箱的行、列坐标。

定义所有货箱到对应组内平均坐标距离的总和为：

$ d = \mathop \sum \limits_{i = 1}^{{K_I}} \mathop \sum \limits_{j = 1}^{{K_{in}}} \sqrt {{{\left[ {{x_{t{K_{ij}}}} - \overline {{c_{t{K_i}}}} \left( x \right)} \right]}^2} + {{\left[ {{y_{t{K_{ij}}}} - \overline {{c_{t{K_i}}}} \left( y \right)} \right]}^2}} 。$

(2)

最后计算所有分类货箱平均坐标的均值：

$ C = \frac{1}{n}\sum\limits_{i = 1}^n {\overline {{c_{t{K_i}}}} \left[ {x,y} \right]} 。$

(3)

根据式（1）和式（3）计算所有组内平均坐标到货箱中心坐标距离的总和为：

$ D = \mathop \sum \limits_{i = 1}^n \sqrt {{{\left[ {\overline {{c_{t{K_i}}}} \left( x \right) - C(x)} \right]}^2} + {{\left[ {\overline {{c_{t{K_i}}}} \left( y \right) - C(y)} \right]}^2}} 。$

(4)

因此，结合式（2）和式（4）得到第1个目标函数：

$ \min {F_1} = \frac{d}{D} 。$

(5)

货位优化是对货位进行重新调整、同类聚合，货箱的重新摆放就涉及到货箱的搬运，主要通过水平步进、垂直步进以及货箱出入库实现货箱的重新分配。为满足仓库使用需求，需要使设备整体搬运量最小。各动作所需时间参考表1。

水平移动时货位优化搬运时间为：

$ \mathop \sum \limits_{n = 1}^{{N_r}} {f_h}({x_{{K_{ijt}}}},{x_{{K_{ij\left( {t - 1} \right)}}}}) 。$

(6)

式中：r为有2行货箱，N_r为当前行货箱数量， $| {x_{{K_{ijt}}}} - $ $ {x_{{K_{ij\left( {t - 1} \right)}}}} |$ 为货箱水平移动距离。

出/入缓存区、单个货箱换层操作，货位优化搬运时间为：

$ {\eta _2}{f_v}({y_{{K_{ijt}}}},{y_{{K_{ij\left( {t - 1} \right)}}}}) + {\eta _1}{f_h}({x_{{K_{ijt}}}},{x_{{K_{ij\left( {t - 1} \right)}}}}) ，$

(7)

式中， $\left| {{y_{{K_{ijt}}}} - {y_{{K_{ij\left( {t - 1} \right)}}}}} \right|$ 表示升降平台移动距离。

则货位优化每步搬运时间为:

$ {{{Q}}_{S{{i}}}} = \left\{ {\begin{aligned} &{\mathop \sum \limits_{r = 1}^2 \mathop \sum \limits_{n = 1}^{{N_r}} {\eta _1}{f_h}({x_{{K_{ijt}}}},{x_{{K_{ij\left( {t - 1} \right)}}}})} ，\\ &{{\eta _2}{f_v}({y_{{K_{ijt}}}},{y_{{K_{ij\left( {t - 1} \right)}}}}) + {\eta _1}{f_h}({x_{{K_{ijt}}}},{x_{{K_{ij\left( {t - 1} \right)}}}})} 。\end{aligned}} \right. $

(8)

因此，得到第2个目标函数：

$ \min {F_2} = T{{\text{Q}}_{S{{i}}}} 。$

(9)

式中，T为货位优化总搬运量。

将聚合度及搬运量目标函数统一，得出总的优化函数：

$ R = {\omega _1}{F_{\text{1}}} + {\omega _2}{F_2}。$

(10)

由于上述2个结果不是统一单位，需要做归一化处理。使用层次分析法( analytic hierarchy process，AHP)对目标函数进行权重分析，得到权重系数为 $ {\omega _1} $ =0.6852， $ {\omega _2} $ =0.3148。

根据该自动化存取系统货箱运动， $ \min {R_F} $ 和 $ \min {R_C} $ 分别表示前一次和当前的优化收益值，可能存在的收益包括：收益增加、收益不变、收益减少，其中收益不变和收益减少均因为做了无效搬运，收益为负，因此收益的设计为：

$ {{reward}} = \left\{ \begin{aligned} &1\quad&{\min {R_F} - \min {R_L} > 0} ，\\ &{ - 1}\quad&{{\text{min}}{R_F} - \min {R_L} \leqslant 0} 。\end{aligned} \right. $

(11)

4）剪枝优化

采用蒙特卡罗搜索策略，基于货位优化收益模型和动作空间，对于当前货箱分布状态S_t，对每一个可能采样的动作a∈A，都进行H轮采样，因此，每个动作a都会得到H组经历完整的状态序列。即

$ \left\{ {{S_t},a,R_{t + 1}^h,S_{t + 1}^h,A_{t + 1}^h, \cdots ,S_T^h} \right\}_{h = 1}^H\text{～}{M_{{v}}},{\text{π}} 。$

(12)

对于每个状态及其对应组合，可以通过统计状态序列来计算其动作价值函数并选择最优的动作。随后，创建一个由已经访问过结点和动作所组成的树，统计树内的每个状态行为价值进行评估；选择当前状态S_t所能执行动作中评估值最大的子节点作为后续搜索起点，达到剪枝效果。

2 改进型MCTS算法设计

MCTS算法属于强化学习的一种，对路径规划、序贯决策问题具有良好适应性^[11]，且能够在拥有较少专业知识的情况下仍能够有较好收敛效果，本文基于自动化存取系统货位优化问题提出兼顾节点收益的蒙特卡洛树搜索的货位优化算法。求解货位优化问题的总体思路是将货位优化过程看作成一个模拟随机货位运动的过程，以当前状态得分作为货位优化效果。然后依据数学模型中的约束关系制定规则，以模型中定义的收益最大化为优化目标，整个搜索过程包括选择、扩展、模拟和更新４个阶段。

MCTS算法每次迭代均通过树策略选择下一个节点进行扩展，不断从扩展节点开始，递归地选择得分最高的货位优化最终状态（循环时间到时停止）。在MCTS中通过树的方法遍历所有可能动作空间，其中，选择步骤被称为树策略，该策略统计分数由上限界限信心（upper confidence bound，UCB）方程给出：

$ {V_{UCB}} = \frac{{Q\left( {{v_i}} \right)}}{{N\left( {{v_i}} \right)}} + c\sqrt {\frac{{{\text{ln}}\left( {N\left( v \right)} \right)}}{{N\left( {{v_i}} \right)}}} 。$

(13)

其中， ${V_{UCB}}$ 表示该状态下搜索树某节点的 $UCB$ 得分， $Q$ 为树策略遍历并选择该节点累计价值的函数，状态v_i为本次搜索根节点v 经过扩展后的第i 个子节点， $Q\left( {{v_i}} \right)$ 为在v节点处进行i动作并进行后续动作获得的总得分，N为获取节点累计遍历次数的统计。因此， $N\left( v \right)$ 为节点v的所有搜索次数，Q(v_i)/ N(v_i)强调了对前续搜索结果的利用；c为用于调整公式前后2部分在整体得分中的比例。因此，该系数较大时算法侧重广度搜索，偏小时该算法则侧重深度搜索。

根据文献[12]中提出的在游戏中增加节点偏差项的思想，通过在UCB方程中添加该偏差项来保障收益变化幅度大的节点被优先搜索，该方法不仅兼顾收益稳定的节点，同时兼顾收益变化幅度大的节点，确保得到各个节点准确的收益估计，保证了分支搜索的合理性。针对货位优化问题，本文目标是动态制定满足搬运量最小且同类型货箱聚合度最好的货位分配方案，通常采取奖励值最高的方案。

由于MCTS循环试探结果具有一定波动性，会出现库存分配较差的结果，由于这些奖励值较差的方案在货位优化过程中被采用的概率较低，没有实际参考意义，但是其对UCB算法中的平均奖励值因数影响较大，为了削弱少量较差的模拟对UCB值的影响，在Schadd等基础上又对考虑偏差的UCB算法进行以下改进：1）随机选取节点上90%模拟结果计算平均奖励值；2）对于围棋等对弈游戏，获取最高奖励值依赖对手选取较差的动作，在动作选择时不能考虑最高奖励值，但提出的货位问题类似于单人游戏，不用考虑对手带来的不确定性，因此节点选择时可以考虑节点最大奖励值。改进后的UCB公式如下：

$ \begin{split}{V_{UCB}}^{1} = &0.5 \times Q{\left( {{v_i}} \right)^{\max }} + 0.5 \times Q\left( {{v_i}} \right)_{_{random}}^{90\% } +\\ &\frac{{Q\left( {{v_i}} \right)}}{{N\left( {{v_i}} \right)}} + c\sqrt {\frac{{{\text{ln}}\left( {N\left( v \right)} \right)}}{{N\left( {{v_i}} \right)}}} 。\end{split}$

(14)

其中： $ Q{\left( {{v_i}} \right)^{\max }} $ 为节点i上所有模拟结果中的最高分；第2项 $ Q\left( {{v_i}} \right)_{_{random}}^{90\% } $ 为节点i上随机选取90%模拟。

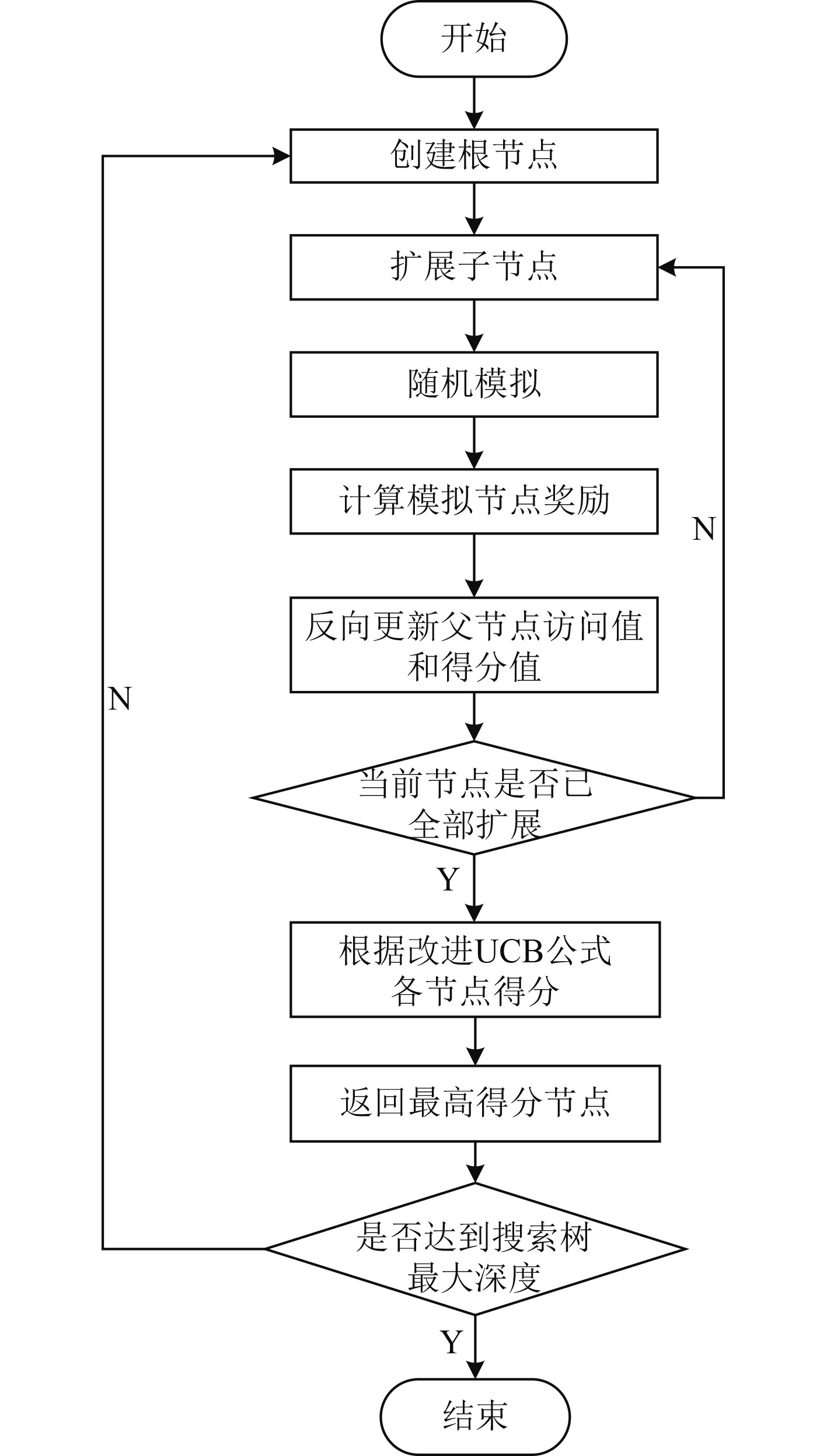
改进后的MCTS算法搜索流程如图3所示。具体步骤如下：

步骤1　初始化系统，根据当前库存状态创建根节点，选择根节点作为当前节点；

步骤2　判断当前是否已达到限定的搜索树最大深度，如果未达到最大深度则继续，否则，结束搜索；

步骤3　 判断当前节点状态，如果没有子节点可以扩展，则根据公式（14）计算得分，返回得分最高的子节点；否则，根据表1随机选择库位优化动作，继续进行扩展；

步骤4　根据步骤3得到的最优可扩展子节点，随机选择下一步策略对此子节点进行模拟，对当前情况进行模拟，直到判断出胜负或到达循环限制，返回该节点模拟得分；

步骤5　将该节点模拟得分进行回溯上传，回溯时，累加各节点访问次数、得分；

步骤6　遍历当前轮循环根节点的所有子节点，比较各节点得分情况，得到本轮次循环优胜可能性最大的子节点；

步骤7　使用步骤6得到的最优子节点，重复步骤2～步骤6，直至结束。

3 仿真结果及分析

依据上述方法改进的MCTS 算法对某型多载具自动化存取系统货位进行优化排列，实验中使用货位优化模拟器软件，该软件能够根据货位优化算法模拟货位运行动作。本次实验采用3行10列的库存布列，模拟器下自动化存取系统货位初始状态如图4所示，其中类型A和类型B货箱乱序摆放。

图5为货位优化中间状态及优化后的货位摆放结果。其中，货位优化共需61步，耗时约4 h 24 min，可以看出，货位优化后，各类型货物聚合排列，改进后的MCTS货位优化算法能够实现自动化存取系统货位的优化摆放。

随后，为了和改进型MCTS进行比较，设计采用贪心算法思想、采用魔方还原思想和基于普通MCTS的货位优化算法，其中，普通MCTS参数设置为每轮学习500次，共进行50轮循环。采用魔方还原的货位优化算法的思想是在货位优化时，通过换行操作快速建立“基准行”，随后以“基准行”为基础进行货位同类型聚合操作。上述对比共采用100组随机库存样本，货位优化步骤结果取均值，最后得到各货位优化算法的优化所需运行步骤对比，各算法对比结果如表2所示。

根据各算法的货位优化对比结果，采用贪心思想的货位优化算法在货箱规模较大时，收敛速度明显较慢，采用魔方还原思想的货位优化算法由于其通过快速小范围的水平、垂直操作，货箱已经达到部分聚合，快速形成“基准行”，随后货箱只通过较少移动便达到优化效果，因此能够优于基于贪心算法和普通MCTS算法。改进型MCTS算法在货箱较少时优势并不明显，当库存大幅度增加后，模拟动作样本数更多，能够更好地选择后续优化步骤，从而取得较好优化效果。

4 结　语

为实现某型多载具自动化存取系统货位优化排列问题，从优化问题的描述、数学模型的建立、算法的选择及优化等多角度对货位优化算法进行分析、设计，提出了一种改进MCTS的货位优化算法，并与贪心等其他货位优化算法进行仿真对比实验，在货位优化时间上表现显著，能够有效解决该自动化存取系统货位优化问题。