近年来,神经网络理论在不断延伸,图像编码得到迅速发展,图像之间存在相似性,利用神经网络编码分析图像之间的自相似性,然后进行压缩,可以很好地实现图像压缩。针对图像压缩,相关领域学者做出了较多的研究。通过数据匹配搜索实现数据压缩,但是这样会直接导致压缩时间过长,压缩的复杂度也随之提高[1]。
传统的压缩方法压缩速度难以提高的根本原因主要在于采用的编码方式为全局编码,由于分形理论以全局搜索为基础,所以只能从全局视域实现编码,因此编码时间过长,压缩效果难以达到理想效果。蚁群算法通过图像分割构建更小的搜索空间,通过小波变换方法对数据分辨率进行研究,实现信息匹配,通过这种方法来进行数据搜索,能够很好地解决压缩时间。神经网络通过建立神经元模仿数据系统,从而实现信息处理,能够确保处理后的数据准确率[2]。本文基于蚁群算法和神经网络的船舶图像压缩方法,并通过实验验证了方法的实际应用效果。
1 蚁群算法和神经网络的船舶图像编码首先,需要采用图像分析工具对船舶图像的空间构造进行识别,再划分出不同子图像区域并进行分割。然后利用神经网络算法对识别出的图像构造各部分的相关性进行推算,得到各部分之间部分与整体之间图像的相似性与差异性,并根据其相似性对各部分图像进行解码。通过蚁群算法将各部分图像转化成数据样本,得到蚁群算法聚类形成的船舶图像数据样本空间,将根据蚁群算法得到的数据样本进行平均值运算,得到图像平均灰度值[3-4]。
基于蚁群算法建立的图像数据聚类模型如下式:
| $ {P_{}} = {\left( {\frac{{{k_{}}}}{{{k_{}} + f}}} \right)^2}。$ | (1) |
其中:P表示得到的聚类模型;
根据式(1)可知,在不同情况下,对象状态也不同,如果对象的接受度低于阈值,则对象将会被捡起;如果对象的接受度超过阈值,则对象被放下[5]。
其次,对需要进行处理的图像划分定义域块与值域块,分别对两者图像区域内的要素进行匹配。由于图像元素匹配概率不等,会存在多个图像区域均相匹配的情况。为此,要对各个图像区域进行优化处理。根据参照物进行压缩变换,在保证图像内容不会发生变化的情况下,调整图像域块的分布情况[6-7]。分析蚂蚁数据聚类后的相似性,规则判定公式如下:
| $ g\left( {{N_i},{N_j}} \right) = \sum\limits_{{N_j} \in {arces} \left( {{N_i},r} \right)} {\left( {1 - t\left( {{N_i},{N_j}} \right)} \right)} 。$ | (2) |
其中:
针对图像可能存在纹理偏差方面的问题,对图像进行变换处理时,很可能会导致图像失真。因此,需要对图像分辨率进行小波分析,将目标图像进行三级分解,得到水平垂直与倾斜方向3个维度的分辨率频度分量[9]。将经过三级分解后的高频图像按照对应维度进行分割,运用蚁群聚类算法,导入图像数据样本空间进行数据运算,根据匹配概率对值域块内部元素分类与判断,将所得结果与定义域块数据进行对照分析,如果数据之间的差大于阈值,则2种元素属于不同类别,如果数据差小于阈值,则属于同一类别。
提取图像中纹理信息特征,对各维度信息数据进行编码预测,运用神经网络处理方法对数据之间的相关性进行识别提取,在保证图像内容完整稳定的条件下,对各区域图像关系进行分析处理。通过蚁群算法得到图像各种状态下的数据样本空间,再通过神经网络对图像之间的相关关系进行识别处理,从而能够对图像分辨率进行恢复与提高,修复效果更加精准,图像处理效率更高。
2 基于蚁群算法和神经网络的船舶图像压缩船舶图像内容多样,十分复杂,在对船舶图像进行压缩时,需要考虑目标之间的差异以及噪声。利用蚁群算法进行船舶图像压缩,将蚁群压缩分为两类,根据不同的搜索策略和信息更新手段对图像进行分割,并检测船舶的边缘[10]。由于船舶图像的搜索策略和信息素更新策略存在一定的差异,因此需要对蚁群进行分类,将蚁群分成区域蚁群和边界蚁群,通过2种导向函数控制不同的蚁群选择不同的路径。边界蚁群进行边界的数据搜索和分析,区域蚁群针对非边界地方进行数据搜索,每次区域蚁群完成一次遍历后,进行数据更新,边界蚁群和区域蚁群互相配合,补偿搜索,实现信息更新。在完成多次遍历之后,分析路径内部所有信息,更新信息数据,利用边界蚁群对小范围的数据进行补偿边界搜索,通过精确指导得到信息数据,完成补偿后进行数据补偿,防止由于无效搜索而造成的算法效率过低。
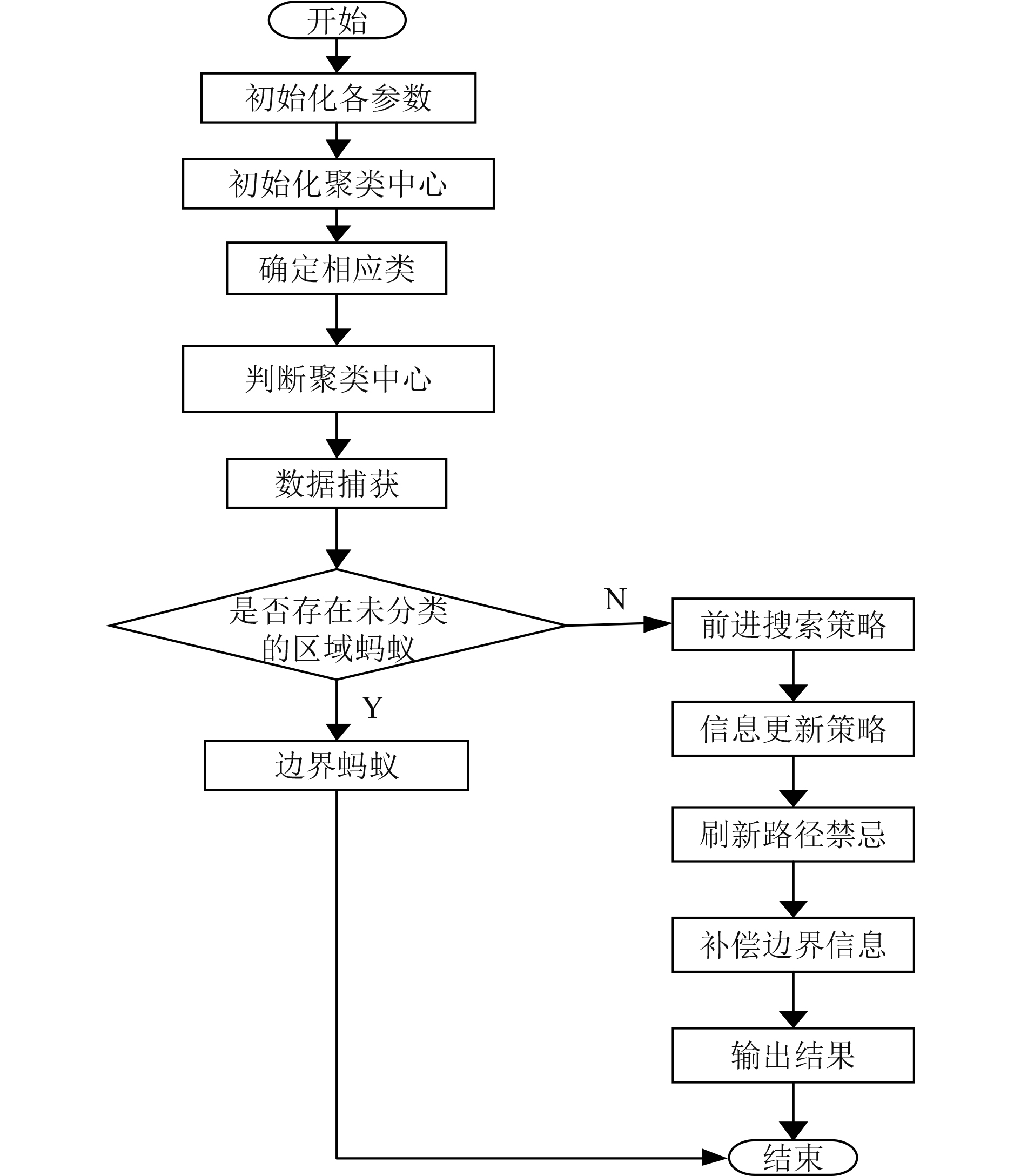
基于蚁群算法和神经网络的船舶图像压缩流程如图1所示。可知,将背景、目标、边缘和噪声组成一幅图像,提取船舶图像的内部特征,根据船舶图像特征区分各种图像信息,从而更好地分析图像信息。通过灰度值确定图像目标和背景,并引入灰度梯度来表述边缘点和噪声点像素周围的灰度值,分析高梯度像素点,将边界点和噪声点引入特征元素,建立3×3像素,得到变量sim=0,通过计算得到领域内部像素点的灰度值差,根据给定阈值计算差值,从而得到三维特征向量,通过表格记录灰度值、灰度梯度值和领域特征值。
|
图 1 蚁群算法和神经网络的船舶图像压缩流程 Fig. 1 The ship image compression process of ant colony algorithm and neural network |
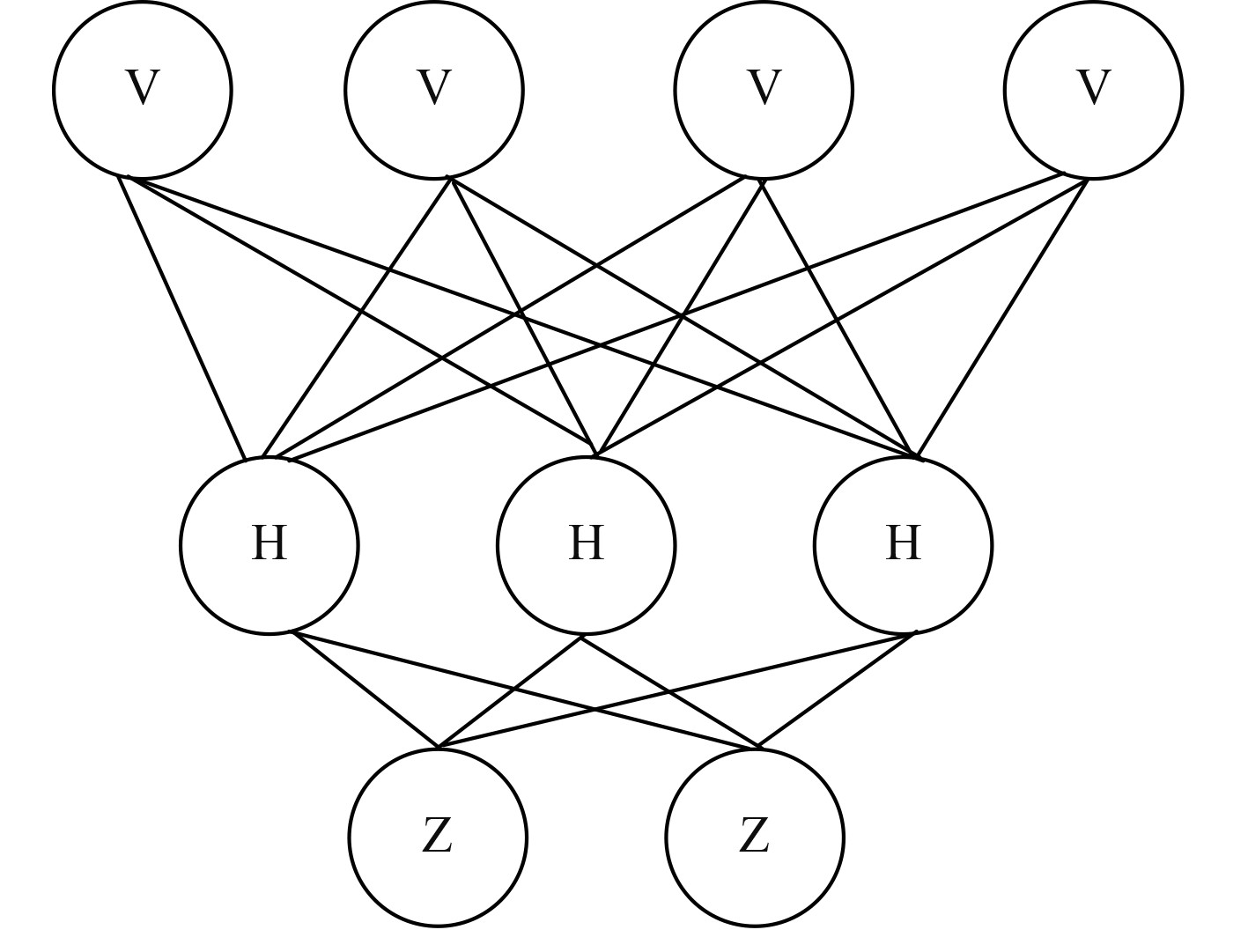
由于随机搜索具有一定的盲目性,会造成无效搜索,因此引入神经网络进行聚类,通过蚂蚁搜索进行引导,通过聚类中心得到目标像素点,分析灰度值,确定不同直方图的峰值,这样能够很好地减少计算量,分析领域特征值,根据梯度判断信息边界和噪声点,确定信息内部的邻域特征值。采集需要压缩图像的信息,并进行备份,通过神经网络将提取图像的各类基本信息按照集合的分类形式进行存储。应用的神经网络如图2所示。
|
图 2 神经网络 Fig. 2 Neural Network |
压缩变换的数据不动点具有稳定性,即
| $ d\left( {{{\bar x}_1},{{\bar x}_2}} \right) \leqslant \frac{1}{{1 - s}}d\left( {{\omega _1},{\omega _2}} \right) 。$ | (3) |
式中:
随机选择图像各类集合中相同数量的像素点信息作为蚂蚁初始化个数,在图像搜索空间内构建一组新的混合图像参数,以此类推,将所有带压缩图像的信息都组合成多个形式的数据参数集合,方便网络数据筛选计算,对图像重构参数的可变半径进行重新设置。当算法输出待压缩图像的蚁群数据聚类结果后,初始化步骤1中采集的所有数据集合,为图像值域匹配搜索提供控制压缩边缘。通过区域蚁群路径进行选择,通过补偿搜索确保边界检测的精确性,由于边界在移动过程中会存在误差,因此需要确定边界信息强度,根据边界信息强度得到真实错觉。设置的启发函数为:
| $ \eta _{ij}^\prime = \frac{{V\left( {{x_j}} \right)}}{{\max \left\{ {1,\left| {{x_j} - {x_i}} \right|} \right\}}} ,V\left( {{x_i}} \right) = \frac{{\displaystyle\sum\limits_{l \in N{E_j}} {\left| {{x_j} - {x_i}} \right|} }}{8}。$ | (4) |
式中:
利用网络网格计算图像数据定域块内的误差加权值并随之携带匹配编码,每次输出单个区域的值域编码后,蚁群算法同时更新匹配概率表,避免网络数据遍历时出现数据冲突,直至算法检测不到压缩图像值域存在空缺编码,输出压缩图像,完成计算。遗传信息与其他蚂蚁进行交流,分析蚂蚁的行动方向,根据状态转移规则对路径进行选择,利用蚁群的相互协作能力对信息进行通信,分析船舶图像像素之间的目的和功能,利用数据信息完成交流,应用的全局更新策略如下式:
| $ {\tau _{ij}}\left( {{t^\prime }} \right) = \rho \cdot{\tau _{ij}}(t) + \sum\limits_{k = 1}^N \Delta \tau _{ij}^k。$ | (5) |
式中:
通过中心搜索内部的边界蚂蚁对数据进行标志,如果像素之间面对面,分析不同像素的距离,如果确定像素相遇,则数据停止。建立禁忌表,从而记录不同数据之间的路径,确定时间阈值,通过时间阈值进行路径返回,限制不同路径密度,防止信息预先定义的数值停止搜索,完成数据压缩。
3 仿真实验为了验证蚁群算法和神经网络的船舶图像压缩方法的有效性,选择分形理论的船舶图像压缩方法、数据挖掘的船舶图像压缩方法进行实验对比。船舶图像为256×256的Lena图像,系统内部的CPU容量为1.7 G,通过256 M的RAM进行数据分析,采用的操作系统为Windows10,通过数据编码将值域块为4×4,实验迭代10次,设定初始数number=36。
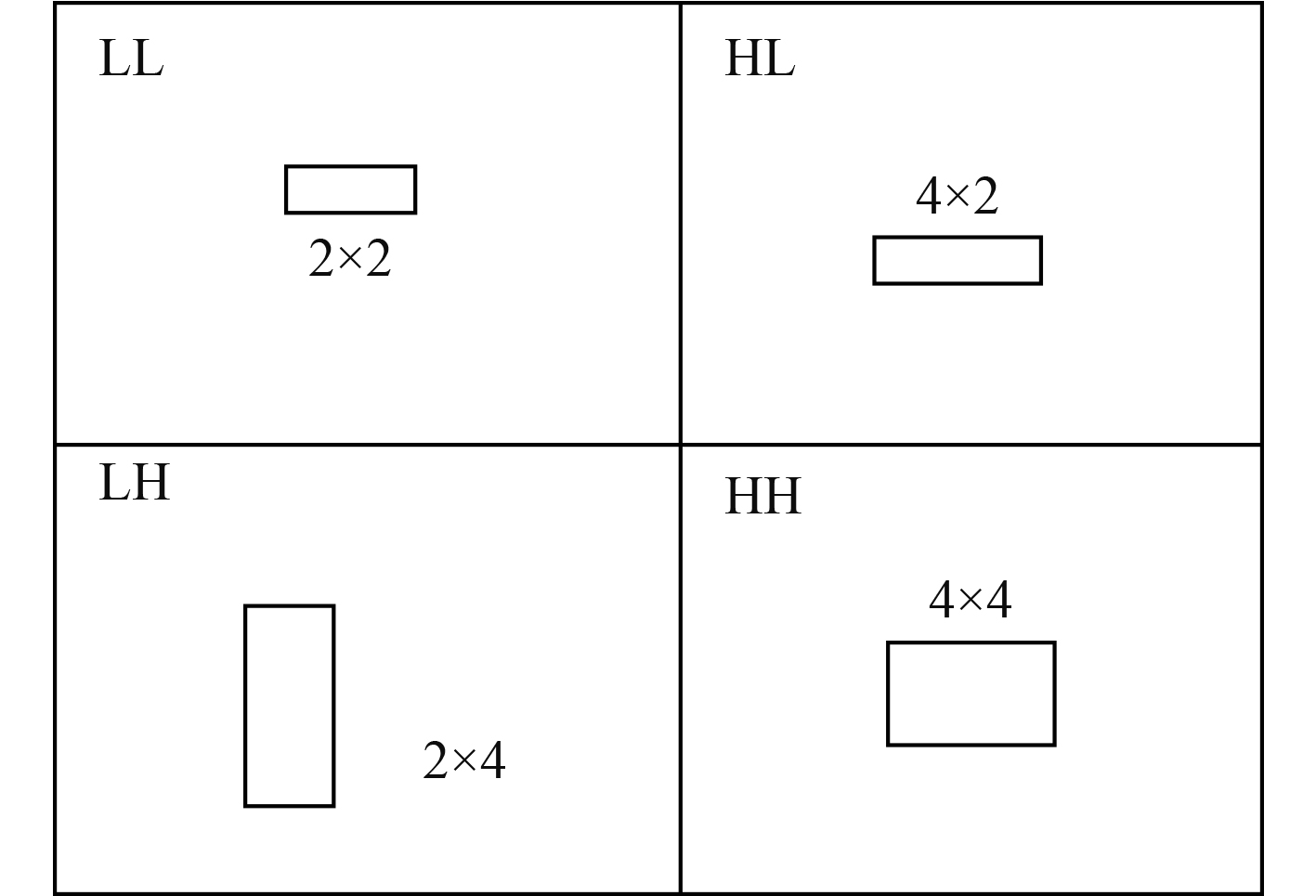
对图像进行分割,得到的分割值域如图3所示。
|
图 3 分割值域 Fig. 3 Splitting the range of values |
选用本文方法和传统方法对船舶图像进行压缩,得到的压缩时间实验结果如表1所示。可知,在6次实验中,利用蚁群算法和神经网络对船舶图像进行压缩花费的压缩时间最短,压缩效率最高。本文提出的压缩方法在对图像质量进行分析和数据编码方面有较大的优势。
|
|
表 1 压缩时间实验结果 Tab.1 Compression time experimental results |
分析图像的压缩比,得到的压缩比实验结果如表2所示。可知,在6次实验中,本文提出的方法压缩比最低,压缩能力更好,在压缩过程中,能够保证图像质量。
|
|
表 2 压缩比实验结果 Tab.2 Compression ratio experimental results |
针对船舶图像进行压缩,选用本文的压缩方法和传统的分形理论压缩方法和数据挖掘压缩方法进行实验对比,得到的压缩结果如图4所示。可知,本文压缩后图像轮廓更加清晰,能够很好地把控纹理细节,通过调节人工调试参数和数据参数实现信息压缩,与传统方法相比,本文方法消耗的时间更少。本文提出的方法能够更好地将船舶图像轮廓分析,压缩后数据更加清晰。

|
图 4 压缩实验结果 Fig. 4 Compression experiment results |
本文利用蚁群算法和神经网络对船舶图像进行压缩,通过数据库转变对船舶图像的分辨率进行分析,采用蚁群算法实现信息编码和聚类,利用定义域块和值域块实现数据搜索,分析图像之间的纹理特征,采用分形预测实现图像压缩,与传统的图像压缩方法相比,本文提出的压缩方法不仅能够缩短压缩时间,同时能够提高压缩比,具有很好的压缩性能。本文压缩方法针对编码率进行了重点研究,但是在执行效率方面研究相对较少,未来需要进一步深入探讨执行效率这一方面的问题,从而确保船舶图像压缩实际应用效果。
| [1] |
南敬昌, 臧净, 高明明. 改进蚁群算法的BRBP神经网络功放逆向建模方法[J]. 激光与光电子学进展, 2020, 57(1): 190-197. |
| [2] |
魏焕新, 张宏国. 深度神经网络结合蚁群算法的躲避攻击多目标对抗方法[J]. 计算机应用与软件, 2020, 37(11): 292-298. DOI:10.3969/j.issn.1000-386x.2020.11.047 |
| [3] |
谢云, 李志中, 唐广花, 等. 卷积神经网络的舰船图像快速无损压缩算法[J]. 舰船科学技术, 2020, 42(10): 62-64. DOI:10.3404/j.issn.1672-7649.2020.10.013 |
| [4] |
莫小芹, 魏进国, 付鹏浩. 基于图像处理技术的玉器自动比对鉴证溯源方法[J]. 工程技术研究, 2021, 6(23): 194-196. DOI:10.3969/j.issn.1671-3818.2021.23.059 |
| [5] |
孙洁, 于孟晗. 轧钢加热炉钢坯温度神经网络预测模型[J]. 国外电子测量技术, 2021, 40(9): 24-28. |
| [6] |
张达明, 何小海, 任超, 等. 基于自适应下采样和超分重建的图像压缩框架[J]. 太赫兹科学与电子信息学报, 2020, 18(2): 298-305. DOI:10.11805/TKYDA2018376 |
| [7] |
邓浩然, 吕成文, 陈东来, 等. 蚁群算法在土壤质地高光谱预测建模中的应用[J]. 土壤通报, 2021, 52(5): 1063-1068. |
| [8] |
周建新, 黄剑雄. 基于改进蚁群算法的加热炉温度控制研究[J]. 机床与液压, 2020, 48(18): 157-162,195. DOI:10.3969/j.issn.1001-3881.2020.18.023 |
| [9] |
李志军, 杨楚皙, 刘丹, 等. 基于深度卷积神经网络的信息流增强图像压缩方法[J]. 吉林大学学报:工学版, 2020, 50(5): 1788-1795. |
| [10] |
张红梅, 严海兵, 张向利. 结合半波高斯量化与交替更新的神经网络压缩方法[J]. 计算机工程, 2021, 47(5): 80-87. |
 2022, Vol. 44
2022, Vol. 44
