随着船舶结构朝着多样化、复杂化方向发展以及对船舶性能要求的不断提高,传统的船舶设计制造技术已经无法满足现代船舶先进的设计制造以及市场的发展需求。利用现代信息技术进行船舶的数字化生产制造,已经成为现代船舶企业提升自身竞争力的重要方法。船舶的数字化设计贯通了船舶设计生产的整个周期,涉及范围十分广泛,本文基于目前船舶设计生产的实际情况以及发展要求,以降低船舶设计生产周期、提高开发效率以及扩大经济效益为目标,着重研究船舶的数字化设计技术以及分段测量数据匹配计算方法,为提高船舶的设计制造技术提供参考。
1 船舶的数字化设计技术 1.1 船舶数字化设计平台船舶的数字化设计生产内容主要包括船舶的设计、生产制造、管理控制、经营决策以及船舶的维护数字化5个方面。船舶数字化设计框架的重点在于利用船舶的3D设计技术构建船舶的3D数字化模型,并且使用现有的比较成熟的工具和算法,在构建船舶3D模型之前进行设计参数的获取,以及船舶3D模型构建之后对构建出的船舶3D模型进行计算、分析。因此船舶数字化设计平台在构建过程中需要考虑船舶数字化建模的短周期、不同设计人员之间的协同性、各设计阶段之间的继承性以及可回溯性等一系列技术问题。本文提出的船舶数字化设计平台结构如图1所示。

|
图 1 船舶数字化设计平台 Fig. 1 Ship digital design platform |
可以看出,在进行船舶的数字化设计过程中,首先进行船舶的船体曲面设计,然后基于船舶的船体曲面进行船体结构建模以及船体数字建模,因此船体曲面设计是船舶一切数字化设计的基础,船舶其他的数字化设计均是基于船舶的曲面设计的。基于船体曲面模型,可以对船舶的性能进行估算,并且可以提取船舶曲面数字模型上的任意曲线,基于这些曲线可以对船舶的结构进行分舱设计。通过配置船舶结构的几何参数,可以对船舶的结构进行参数化设计,考虑到参数化设计的便捷性,通常使用船舶的参数化设计进行舱壁以及舱室的建模。
全船结构模型的构建是在船舶数字曲面模型的基础上并且以舱段为单位,建立每个舱段的数字模型,同时对船舶结构的数据信息进行管理。船舶数字模型中不同部分的属性是通过船舶数字模型中的特征来描述的,船舶的实体制造技术就是利用船舶数字模型中的三维结构拓扑信息来精确地对船舶的几何形状进行表示,因此以特征信息为基础的船舶参数化建模,就是利用船舶数字模型的特征信息集进行船舶结构的参数化处理,最终构建出船舶的三维结构模型。
船舶数字化设计核心是实现船舶数字模型信息的分布式共享,船舶数字模型信息的分布式共享是以船舶的结构为基础,将计算量巨大的船舶数字造型操作在服务器中执行,船舶数字化设计平台的客户端可以给用户提供船舶模型观测以及操作的界面,并且可以提供船舶结构造型系统的应用接口。
船舶快速设计是基于分布式计算环境,以船舶整体设计为目标,将船舶结构的设计流程进行切分细化,同时基于模块化的船舶组件库,对分解之后的船体结构进行构建,这样可以实现船舶结构的快速建模以及修改。
1.2 船舶数字建模设计船舶数字建模设计主要包括NURBS船体曲面数字模型建立、船舶参数化分舱设计2个内容。
作为复杂双曲面,船体曲面无法利用解析曲面进行数学描述,在对船舶进行数字船体曲面模型构建之前要先获得构建型线所需要的点信息,利用差值运算的方法进行船体曲面网格模型的构建,最终可以得到船舶整体的曲面模型。船舶结构表面的离散坐标使用型值表来表示,使用插值运算方法对型值表中的数据进行计算,则可以构建船舶的船体型线。在船舶的坐标系中,假设船长方向、船深方向、船舶的左舷方向分别为X轴、Y轴以及Z轴,船舶数字化设计系统图形界面中的原点为坐标系的原点,由于船舶的型线有着造型灵活等特点,因此为确保船舶型体曲线的计算精度,采用非均匀有理B样条曲线来描述船舶的型体曲线,分段有理B样条的数学模型如下式:
| $ p\left( u \right) = \sum\limits_{i = 0}^n {{p_i}{R_{i,k}}\left( u \right)} 。$ | (1) |
式中,K次有理基函数Ri,k(u)可以用下式表示:
| $ {R_{i,k}}\left( u \right) = \frac{{{W_i}{N_{i,k}}\left( u \right)}}{{\displaystyle\sum\limits_{j = 0}^n {{W_j}{N_{j,k}}\left( u \right)} }}\text{。} $ | (2) |
式中:Pi为多边形的控制点;Wi为多边形控制点的权重系数。权重系数Wi可以对区间[ui,ui+k+1]内的船舶曲线形状产生影响,因此权重系数Wi具备局部特性,这样可以十分便捷地对船体曲线进行分段加工处理,并且可以自由地对船体曲线的局部形状进行修正。当船舶的型线模型中同时含有B样条曲线以及直线的时候,在曲线设计上既要确保曲线和直线之间的分离,又要保证曲线和直线之间的连续性以及相切等特点。当完成船舶型线模型的构造之后,则可以基于船舶的型线模型进行船体曲面模型的构建。作为一种可以对控制点进行加权运算的曲面,NURBS曲面通常可以使用对控制点坐标进行修改或者对控制点的权重系数进行修改来进行船舶曲面的设计,并且这种修改设计方法只会影响到船舶的局部曲面的形状,因此船舶曲面通常使用双参数变量的B样条曲线来表示,如下式:
| $ p\left( u \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{W_{i,j}}{P_{i,j}}{N_{i,k}}\left( u \right){N_{j,l}}\left( v \right)} } }}{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{W_{i,j}}{N_{i,k}}\left( u \right){N_{j,l}}\left( v \right)} } }}\text{。} $ | (3) |
式中:Pi,j为网格阵列中的控制顶点;Wi,j为控制顶点的权重系数,网格阵列中四角控制点的权重系数大于0,其他地方控制点的权重系数大于等于0。
在船舶曲面设计过程中,如果直接对船舶曲面进行光顺处理,计算机系统则会花费很长的时间进行运算,因此本文直接对船舶曲线进行光顺处理,基于船舶曲线的光顺处理,计算机运行时间较短,同时也有助于对船舶曲线模型进行修改。通常使用圆率序列法来获得一条曲线变化均匀且无拐点的光滑船舶曲线,该计算方法是求解船舶曲线上任意三点的圆率k,公式如下:
| $ k = \frac{{2\sin \alpha }}{l}\text{。} $ | (4) |
式中:l为船舶曲线上三点所构成的圆弧的弧长;α为圆心角的一半。
船舶的分舱设计是指采用多个船舶甲板、舱壁等船舶部件对船舶结构进行合理划分,并且在划分过程中,要确保船舶内部空间的利用率足够大,同时能够提高船舶抗沉能力。船舶的分舱设计是一个不断修改以及完善的过程,为了提高船舶的设计效率,通常利用参数化设计对船舶的结构进行分舱设计。参数化设计使得船舶的模型具备可重构性以及可并行设计等特性,因此在船舶舱壁设计的过程中使用参数化方法,该方法又被叫做尺寸驱动,这使得船舶的CAD软件系统具备交互式模型设计功能。船舶分舱的参数化设计方法的核心是约束造型,船舶的几何约束代表了不同特征层次的元素之间的约束关系以及位置关系,船舶结构和尺寸约束如下式:
| $ C = \left( {T,01,02,V} \right)\text{。} $ | (5) |
式中:C为船舶约束;T为船舶约束类型;01和02为约束目标;V为约束值。
1.3 船舶结构建模方法船舶结构建模是先对船舶的板、梁、骨架尺寸进行定义,同时添加结构设计约束以及相互依赖关系,最后获得船舶的设计参数。船舶结构的建模方法如图2所示。可以看出,在对船舶的结构进行建模的过程中,首先构建出船体的型线、曲面以及分舱等模型,然后进行船舶结构的模型设计,在构建船舶结构模型的过程中分成货舱、船首、船尾以及机舱等部分,并分别进行结构建模,得到各部分结构模型之后,则可以对这些结构模型进行信息计算分析,例如重量重心、材料统计、振动计算、有限元分析等,并对计算出的结果进行总结分析,将计算结果不符合设计要求的结构模型进行快速地修改,一直修改到计算结果符合设计要求为止。

|
图 2 船舶结构建模方法 Fig. 2 Ship structure modeling method |
船舶分段测量技术可以分成接触式和非接触式2种。由于船舶分段结构都比较大,因此采用接触式测量技术进行测量效率比较低、时间比较长。采用基于全站仪的非接触式测量技术,全站仪是以光的直线传播以及波速稳定为基础,根据测量两点之间的电磁波传输延时,间接地测量出直线距离。船舶分段结构测量的核心思想是根据船舶分段结构的特点提前标定管理点位置,然后使用全站仪对坐标系中管理点位置的坐标进行测量,这样可以避开接触力导致的系统和随机误差。船舶结构分段特征点和设计点之间的偏差,需要在测量点的数据信息和船舶分段模型设计点的数据信息之间进行坐标匹配来调整。
全站仪测量系统可以完成电子测角的测量、距离的测量,以及相关测量数据存储等工作,该系统的基本测量原理如图3所示。可以看出,利用全站仪进行船舶结构分段测量的过程中,根据船舶分段结构摆放的角度,设计出合理的全站仪测量坐标系,在该坐标系中全站仪定义为原点,水平面、垂直方向、水平方向分别为坐标系的XOY面、Z轴、Y轴,根据右手定理确定X轴,则坐标系中点Si的XYZ坐标如下式:

|
图 3 全站仪测试原理 Fig. 3 Test principle of total station |
| $ \left\{ {\begin{array}{*{20}{l}} {{X_{i,s}} = S \cdot \cos \beta \cdot \cos \alpha },\\ {{Y_{i,s}} = S \cdot \cos \beta \cdot \sin \alpha } ,\\ {{Z_{i,s}} = S \cdot \sin \beta } 。\end{array}} \right.$ | (6) |
式中:S为斜距;α为天顶角;β为水平角。
2.2 船舶数据匹配技术在船舶分段结构测量数据和设计数据匹配过程中,首先通过初始变换,将船舶分段结构的实际测量点的坐标转变到设计点坐标系中,接着使用四元数粗配准方法,降低船舶分段结构测量点坐标和船舶分段设计模型之间因坐标旋转而产生的误差,同时该方法可以对船舶的数据模型进行旋转矩阵的求解。使用基于ICP迭代的最大似然估计算法,对船舶分段测量数据进行精匹配,使得船舶分段测量数据和船舶设计数据之间最贴近,降低两者之间的坐标以及距离的偏差,实现2个数据坐标集的二次匹配。ICP算法是通过最小二乘法转换过来的,该算法要求待匹配的2个数据集之间的偏差不能过大,否则无法得到理想的匹配结果。
ICP算法的核心在于使用全站仪测出船舶分段结构体表面的特征点数据集s,并且数据集s要包含于设计数据集m中。对船舶分段结构测量点集s中的任意坐标点进行初始变换,并在设计数据集m中找出最接近的设计点,构建出一一对应的关系,然后根据迭代ICP算法进行迭代计算,直至满足设计阈值为止。两特征点集的配准变换的目标最小函数如下式:
| $ \min {\text{ }}d\left( {{R^k},{T^k}} \right) = \sum\limits_{i = 1}^N {{{\left[ {{R^k}{s_i} + {T^k} - {m_i}} \right]}^2}} \text{。} $ | (7) |
当式d(Rk,Tk)=0时,意味着船舶分段结构测量点集和设计点集完全重合。通过对目标最小函数误差的解算,可以获得数据配准参数Rk,Tk,那么船舶分段结构测量点集和设计点集之间的配准误差如下式:
| $ \min {\text{ }}{d^k} = \sum\limits_{i = 1}^N {{{\left[ {{R^k}{s_i} + {T^k} - {m_i}} \right]}^2}} \text{。} $ | (8) |
经过k次迭代之后,船舶分段结构测量点集和设计点集之间的距离估计如下式:
| $ {e^k} = \sum\limits_{i = 1}^N {\left\| {m_i^k - s_i^k} \right\|} _2^2\text{,} $ | (9) |
假设配准误差的阈值要求为dk≤ek,则船舶分段结构的测量点集和船舶设计点集之间的距离估计如下式:
| $ {d^k} = \sum\limits_{i = 1}^N {\left\| {m_i^k - s_i^{k + 1}} \right\|} _2^2\text{,} $ | (10) |
在第k+1次迭代过程中,船舶分段结构的测量点集sk+1中的任意一点sk+1 i,都可以在船舶设计点集sk+1中找到最近的点mk+1 i,如下式:
| $ \left\| {m_i^{k + 1} - s_i^{k + 1}} \right\|_2^2 \leqslant \left\| {m_i^k - s_i^{k + 1}} \right\|_2^2\text{。} $ | (11) |
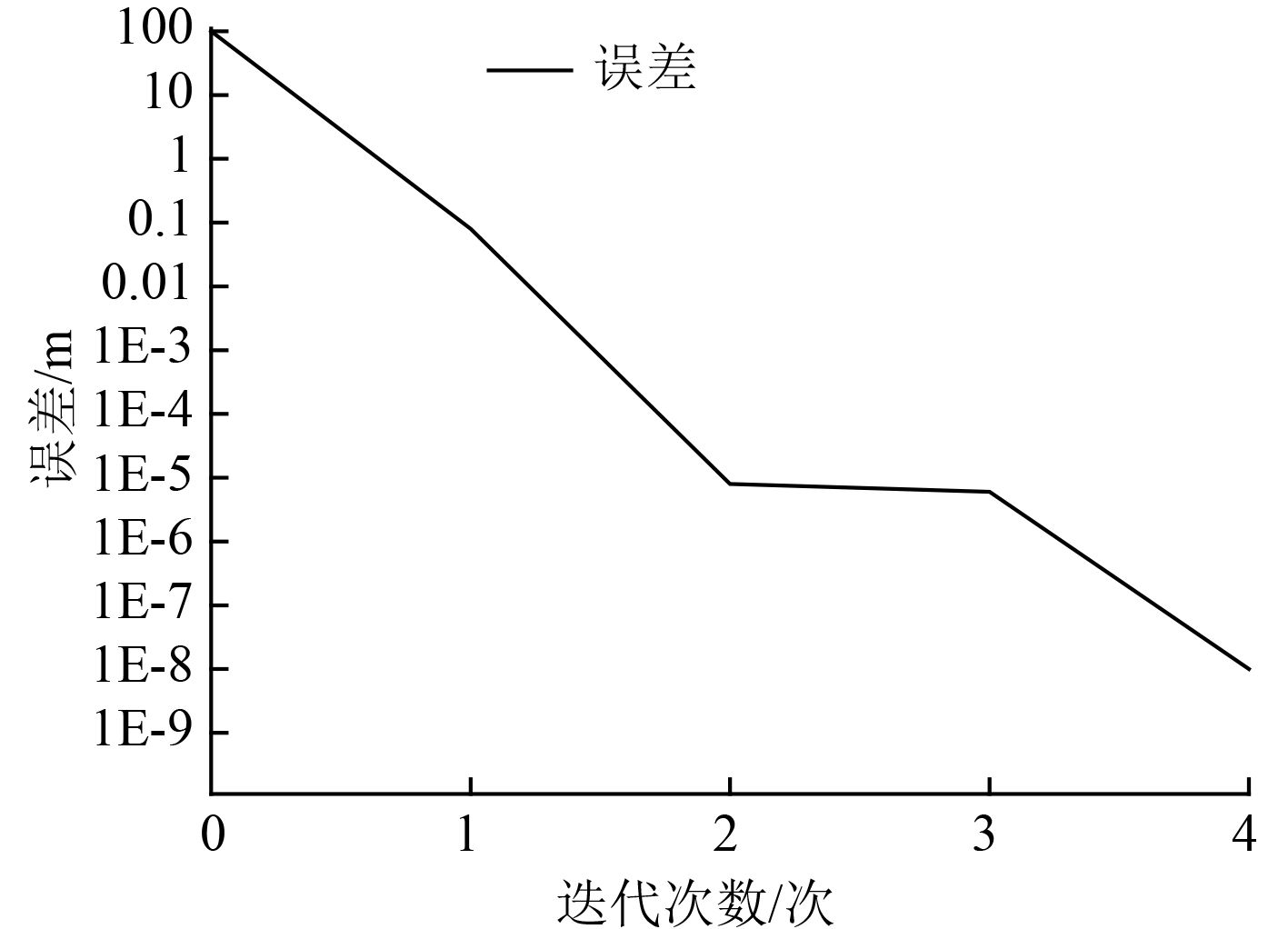
ICP算法迭代次数所对应的误差如图4所示。
|
图 4 ICP算法迭代次数和误差曲线 Fig. 4 Iteration times and error curve of ICP algorithm |
现代化船舶设计制造要求在确保船舶质量的情况下,最大化地降低船舶的设计周期,提升船舶的设计效率,降低船舶的设计缺陷。为了适应这种发展趋势,船舶的数字化设计技术应运而生,为船舶的设计生产带来了新的技术支持。本文研究了船舶的数字化设计技术以及分段测量数据匹配计算方法,有助于促进船舶工业设计技术的发展。
| [1] |
郝江凌, 单雄飞, 赵利宁, 等. 电子海图导航系统的研究进展与未来趋势[J]. 大连海事大学学报, 2021(47): 1-7. HAO Jiang-ling, SHAN Xiong-fei, ZHAO Li-ning, et al. Research progress and future trend of electonic chart navigation system[J]. Journal of Dalian Maritime University, 2021(47): 1-7. |
| [2] |
甘丽霞. 基于增强现实技术的船舶智能导航系统[J]. 舰船科学技术, 2021, 43: 118-120. GAN Li-xia. Design of ship intelligent navigation system based on augmented reality technology[J]. Ship Science and Technolgoy, 2021, 43: 118-120. |
| [3] |
龚茜茹, 赵建超. 卫星导航系统的船舶航行轨迹智能跟踪方法[J]. 舰船科学技术, 2019, 41: 37-39. GONG Qian-ru, ZHAO Jian-chao. Intelligent tracking method of ship’s navigation track information in satellite navigation system[J]. Ship Science and Technolgoy, 2019, 41: 37-39. |
| [4] |
王刚. 船舶导航轨迹识别中智能算法研究[J]. 舰船科学技术, 2016, 38: 142-144. |
| [5] |
李慧真. 基于大数据处理技术的界面交互设计研究[J]. 现代电子技术, 2019, 42: 38-41. |
| [6] |
李静, 东星, 曾健友. 船舶推进监控系统终端显示界面交互设计方法[J]. 舰船科学技术, 2021, 43: 109-111. Li Jing, DONG Xing, ZENG Jian-you. Interactive design methond for terminal display interface of ship propulsion monitoring system[J]. Ship Science and Technolgoy, 2021, 43: 109-111. |
| [7] |
刘岗, 陈超, 赵轶男, 等. 作战指挥控制系统人机交互设计流程研究[J]. 包装工程, 2020, 41: 85-91. |
| [8] |
马超民, 赵丹华, 辛灏. 基于用户体验的智能装备人机交互界面设计[J]. 计算机集成制造系统, 2020, 26: 2650-2660. |
 2022, Vol. 44
2022, Vol. 44
