2. 海军航空大学信息融合研究所,山东 烟台 264001;
3. 海军航空大学航空基础学院,山东 烟台 264001
2. Department of Information Fusion, Naval Aviation University, Yantai 264001, China;
3. School of Aviation Basis, Naval Aviation University, Yantai 264001, China
目前,在海战场通信这种非合作通信环境中,往往存在大量未知的通信信号,这些信号通常来源、性质或者内容未知,这对于舰船通信对抗是一种挑战。如何有效区分这些信号,在舰船通信电子战中掌握主动权,进而掌握海战场的战场态势,是目前亟待解决的一类问题。而这其中最首要的一项技术便是识别出接收信号的调制方式类别。
通信信号调制识别的步骤主要分为预处理、特征提取和分类识别[1]。早期的调制识别,主要是通过频域分析,提取不同调制信号的频域差异来识别不同的调制类型[2-3]。在高斯白噪声条件下,Ghani[4]提出了基于功率谱和谱峰数量的调制识别方法,有效识别了AM,QPSK等10种不同调制类型的调制信号。但是该方法仅限于高斯白噪声信道,对于瑞利衰落信道、莱斯信道等乘性噪声信道则没有研究。1998年,Desinio[5]提出采用信号谱特征来进行通信调制识别的算法,但仅能识别有限种类的调制信号,实用性较差。Huo等[6]提出了基于星座点Hellinger特征量的通信调制识别方法,相比于文献[5],此算法能够完成多种类的调制识别任务。
上述算法虽能一定程度识别不同调制类型的通信信号,但在识别过程中易受噪声影响,算法的抗噪性能较差。对此,信号的高阶累积量开始作为调制信号的特征参数进行调制识别,该信号特征具有抗噪性能强的特性。Lopatka等[7]提出了基于高阶矩累积量的调制识别方案,该算法在低信噪比环境下显著提升了调制识别性能,且无需获得噪声等先验信息。但该算法的缺点在于算法的复杂性引入了大量的计算量,导致识别的实时性较差。Swami等[8]提出了基于信号的4阶累积量的通信调制识别方案,该方法在载波相位和频率偏移、非高斯白噪声情况下具有较强的噪声鲁棒性,但算法的复杂度与计算量进一步增大。Maliatsos等[9]首次采用小波变换进行调制识别,先通过小波变换提高抗噪性能,然后提取信号小波特征参数进行调制识别,实现了PSK,FSK,ASK和QAM的多种调制方式的识别,同时降低了计算复杂度。但该算法在低信噪比环境下的识别性能没有进行讨论,具有一定缺陷。
上述识别方法均是基于人工预定义特征提取的调制识别方法,需要人工设计特征参数的提取,当选择的特征参数不适用于所识别的调制类型时,会严重影响识别效果。因此,基于人工预定义特征提取的调制识别方法泛化能力弱。对此需要找到一种鲁棒性更好、适用范围更广的调制识别方法是至关重要的[10]。2016年,Timothy等[11]提出了基于卷积神经网络(convolutional neural network,CNN)的调制识别方法,实现了11种调制信号的识别分类。实验表明,该方法优于传统的特征提取的识别方法,在识别种类和准确率上都得到了提高。此算法的本质也是基于特征参数提取的调制识别算法,只不过特征参数的确定是通过神经网络模型进行训练学习得到,能够自适应地提取特征,直接从接收到的原始信号进行特征提取和分类。同时,相比于SVM和决策树等传统的机器学习方法,基于神经网络模型的调制识别算法的识别率得到了极大的提高。但是由于训练样本的影响,对部分调制类型的识别区分度不是特别理想。2017年,Krishna等[12]提出了基于深度神经网络(hierarchical deep neural networks, H-DNN)的识别方法,该方法解决了文献[11]中对WBFM识别率不高的问题,但对于4-QAM和16-QAM两种调制方式的识别率不理想。2018年,Li等[13]提出了基于深度卷积神经网络的鲁棒自动VHF用于调制识别,该方法提高了抗噪声性能和算法的鲁棒性,但是识别种类有所降低,共识别了7种调制方式,同时网络复杂度有所增加。
针对传统基于卷积神经网络的通信调制识别方法存在的易受噪声干扰缺陷,本文提出一种基于卷积神经网络与对抗训练的调制识别方法。选择卷积神经网络作为深度学习的模型,通过卷积核自适应提取调制信号的特征参数,并通过对抗训练的方法提升网络的抗噪性能。最后采用SoftMax层输出识别概率,达到多调制识别的目的。
1 调制识别方法 1.1 通信信号调制原理
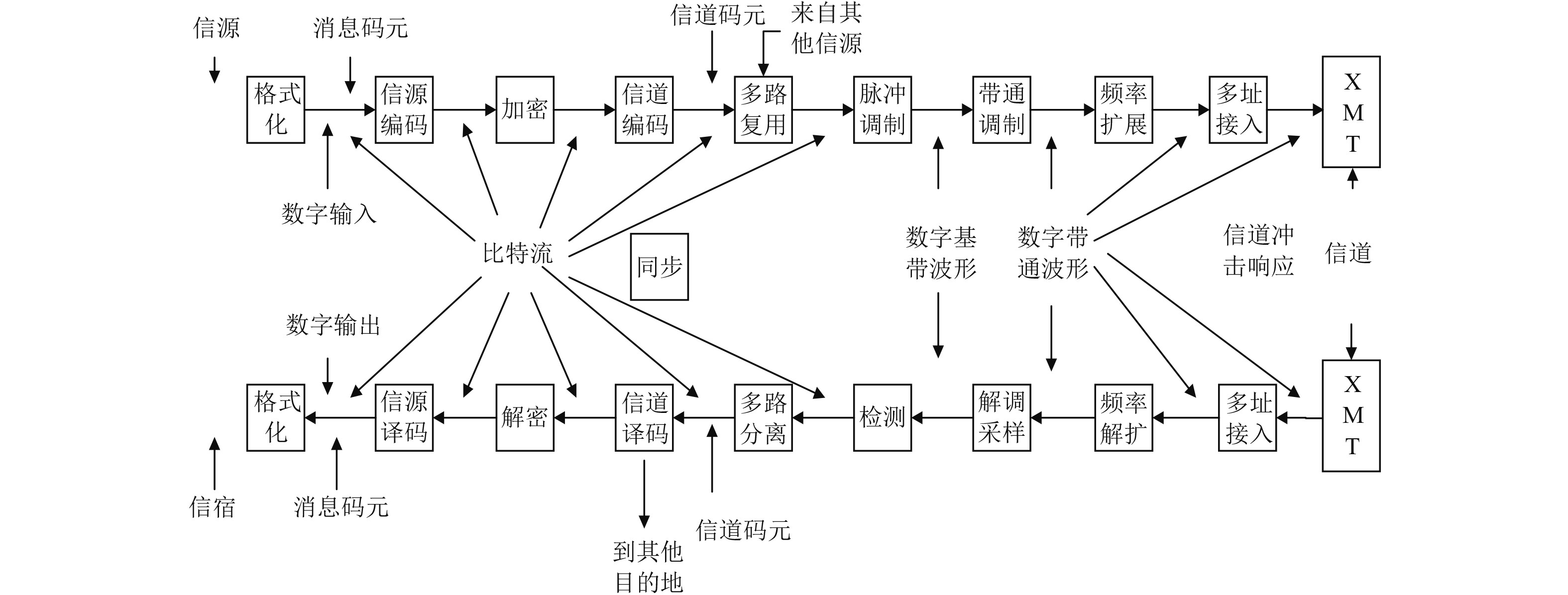
|
图 1 通信信号传输系统 Fig. 1 Communication signal transmission system |
卷积神经网络是一种前馈神经网络,通过卷积核的卷积与平移提取数据的特征,然后通过全连接层来完成特征参数的向量化,以及最终的识别分类[14]。卷积神经网络的结构图如图2所示。

|
图 2 标准卷积神经网络 Fig. 2 Standard convolutional neural network |
可知,送入卷积神经网络的信号数据通过3层卷积层(CNN Ⅰ,CNN Ⅱ,CNN Ⅲ)自适应地提取调制信息的特征参数。经过卷积层的特征提取,特征向量被送入全连接层进行分类处理,进而完成调制识别。其中最后一层全连接层包含K个神经元,对应K个不同的待识别调制类别。
1.3 对抗训练现实情况中,调制信号受到噪声干扰而影响卷积神经网络的特征提取,从而导致误识别的现象出现。为解决传统的卷积神经网络解决此类问题所存在的弊端,本文引入对抗训练算法来提升网络的抗噪性能,进而提升识别系统的泛化能力,最终提升识别性能。
对抗训练可通过如下数学模型表示[15]:
| $ \mathop {\min }\limits_\theta {{E}_{\left( {x,y} \right) \sim D}}\left[ {\mathop {\max }\limits_{\Delta x} J\left( {x + \Delta x,y;\theta } \right)} \right] 。$ | (1) |
式中:
| $ J\left( {x,y;\theta } \right) = - y\log {y_{pre}}\left( {x;\theta } \right) 。$ | (2) |
根据最大梯度下降原理,最优的人工噪声扰动
| $ \Delta x = {\nabla _x}J\left( {x,y;\theta } \right) ,$ | (3) |
对其进行归一化处理得到:
| $ \Delta x = \frac{{{\nabla _x}J\left( {x,y;\theta } \right)}}{{{{\left\| {{\nabla _x}J\left( {x,y;\theta } \right)} \right\|}_2}}} 。$ | (4) |
从而得到人工噪声扰动,又称为对抗样本。
计算得到原始调制信号数据的对抗样本后,通过正则化的形式添加至损失函数中,如下式:
| $ \tilde J\left( {x,y;\theta } \right) = J\left( {x,y;\theta } \right) + \lambda J\left( {\tilde x,y;\theta } \right)。$ | (5) |
根据最大梯度下降法,通过损失函数
| $ {\theta ^{i + 1}} \leftarrow {\theta ^i} - \eta {\nabla _\theta }\tilde J 。$ | (6) |
最终完成卷积神经网络的对抗训练。训练完成的卷积神经网络将用于通信调制信号的识别分类。
2 实验验证与分析 2.1 实验数据库调制识别的数据库来源于Timothy J O'Shea公开的RML2016.04C[16] 和RML2016.10a[17]数据集,该通信调制数据由采样数据的同相分量(Inphase)与正交分量(Quadrature)组成,即I/Q两路数据,其数据样本的维度为128×2。2个数据集包含的通信调制信号数据样本分别为220000和162060[18],共包含11种调制类别。其中模拟调制方式包括AM-DSB,AM-SSB,WBFM,数字调制方式BPSK,8PSK,CPFSK,GFSK,4QAM,16QAM,64QAM和QPSK。这些信号的信噪比(Signal to Noise Ratio,SNR)分别为−20 dB,−18 dB,…16 dB,18 dB。
2.2 网络结构与网络实现因为输入数据的维度为128×2,因此输入层尺寸设置为128×2。卷积层Ⅰ包含128个卷积核,每个卷积核的尺寸为20×2;卷积层Ⅱ包含64个卷积核,每个卷积核的尺寸为20×2;卷积层Ⅲ包含64个卷积核,每个卷积核的尺寸为10×2。卷积层均采用ReLU作为激活函数,具体表达式为:
| $ {ReLU} (x) = \max (0,x) 。$ | (7) |
全连接层Ⅰ的神经元个数为32,其作用是向量化卷积特征参数,将分布式特征表现映射到样本的标记空间;全连接层Ⅱ的神经元个数为11,通过SoftMax分类函数完成分类。
神经网络模型的结构与参数如图3所示。

|
图 3 神经网络模型的结构与参数 Fig. 3 Structure and parameters of the neural network model |
实验验证分别通过上述2组实验数据集开展,并且分别选用信噪比为−12 dB,−8 dB,…,12 dB,16 dB的实验数据集。实验验证过程中,卷积神经网络的训练方式采用常规训练方式与对抗训练方式进行对比,并测试2种训练方式下的不同信噪比下对应的识别率,实验结果如表1和表2所示。
|
|
表 1 采用实验数据集RML2016.04C时,对抗训练与常规训练下调制识别率数值 Tab.1 Modulation recognition rate under adversarial training and conventional training with experimental data set RML2016.04C |
|
|
表 2 采用实验数据集RML2016.10a时,对抗训练与常规训练下调制识别率数值 Tab.2 Modulation recognition rate under adversarial training and conventional training with experimental data set RML2016.10a |
由表1与表2可得,在不同信噪比下,采用对抗训练算法的卷积神经网络的识别性能均有不同程度的提升,特别在低信噪比下,识别性能提升明显。只有在高信噪比下,2种训练方式得到的卷积神经网络的识别性能才大致相同。这是因为此时的数据受噪声污染程度较低,数据质量较好,对抗训练与不进行对抗训练的识别效果才会相同。
图4和图5表示本文算法在0 dB与16 dB信噪比下的识别混淆矩阵。

|
图 4 SNR=0 dB时的识别混淆矩阵 Fig. 4 Recognition confusion matrix with SNR=0 dB |

|
图 5 SNR=16 dB时的识别混淆矩阵 Fig. 5 Recognition confusion matrix with SNR=16 dB |
本文针对通信调制识别问题,提出一种基于卷积神经网络与对抗训练的调制识别方法。选择卷积神经网络作为深度学习的神经网络模型,通过卷积核自适应提取调制信号的特征参数。根据训练数据集计算网络的对抗样本,并添加至原始数据集中,送入神经网络进行对抗训练,以提升网络的抗噪性能。最后采用SoftMax层输出识别概率,达到多调制识别的目的。实验结果表明,对比常规训练方式,采用对抗训练算法训练网络可以整体提升网络的识别性能,特别在低信噪比下,网络的识别性能提升明显。
下一步将重点针对非高斯环境下的通信调制信号的调制识别开展研究,进一步对算法进行创新优化,从而提升算法的实用性。
| [1] |
DOBRE O A, BAR-NESS Y, SU W. Higher-order cyclic cumulants for high order modulation classification[C]// Military Communications Conference, Milcom '03. IEEE, 2003: 112−117.
|
| [2] |
WU H C, SAQUIB M, YUN Z. Novel automatic modulation classification using cumulant features for communications via multipath channels[J]. IEEE Transactions on Wireless Communications, 2008, 7(8): 3098-3105. DOI:10.1109/TWC.2008.070015 |
| [3] |
曾创展, 贾鑫, 朱卫纲. 通信信号调制方式识别方法综述[J]. 通信技术, 2015, 48(3): 252-257. DOI:10.3969/j.issn.1002-0802.2015.03.002 |
| [4] |
GHANI N, LAMONTAGNE R. Neural networks applied to the classification of spectral features for automatic modulation recognition[C]// Military Communications Conference, MILCOM '93. Conference record. Communications on the Move, IEEE, 1993: 111−115.
|
| [5] |
DESIMIO M P, PRESCOTT G E. Adaptive generation of decision functions for classification of digitally modulated signals[C]// Aerospace and Electronics Conference, NAECON 1988. Proceedings of the IEEE 1988 National, IEEE, 1988: 1010−1014.
|
| [6] |
HUO X, DONOHO D. A simple and robust modulation classification method via counting[C]// IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 1998: 3289−3292.
|
| [7] |
LOPATKA J, PEDZISZ M. Automatic modulation classification using statistical moments and a fuzzy classifier[C]// International Conference on Signal Processing Proceedings, IEEE, 2000: 1500−1506.
|
| [8] |
SWAMI A, SADLER B M. Hierarchical digital modulation classification using cumulants[J]. IEEE Translation and Communication, 2000, 48(3): 416-429. DOI:10.1109/26.837045 |
| [9] |
MALIATSOS K, VASSAKI S, CONSTANTINOU P. Interclass and intraclass modulation recognition using the wavelet transform[C]// IEEE, International Symposium on Personal, Indoor and Mobile Radio Communications, IEEE, 2007: 1−5.
|
| [10] |
FAISAL N K, ZHONG Kang-ping, ZHOU Xian. Joint OSNR monitoring and modulation format identification in digital coherent receivers using deep neural networks[J]. Optics Express, 2017, 25(15): 17767. DOI:10.1364/OE.25.017767 |
| [11] |
O’SHEA T J, CORGAN J, CLANCY T C. Convolutional radio modulation recognition networks[C]// International Conference on Engineering Applications of Neural Networks, Springer International Publishing, 2016: 213−226.
|
| [12] |
KARRA K, KUZDEBA S, PETERSEN J. Modulation recognition using hierarchical deep neural networks[C]// IEEE International Symposium on Dynamic Spectrum Access Networks, IEEE, 2017: 1−3.
|
| [13] |
LI R, LI L, YANG S, et al. Robust automated vhf modulation recognition based on deep convolutional neural networks[J]. IEEE Communications Letters, 2018, PP(99): 1-1. |
| [14] |
鲍丹. 非理想条件下的调制分类问题[D]. 西安: 西安电子科技大学, 2007.
|
| [15] |
GOODFELLOW I J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples[EB/OL]. http://arxiv.org/abs/1412.6572.
|
| [16] |
HUAN C Y, POLYDOROS A. Likelihood methods for MPSK modulation classification[J]. IEEE Translation Communication, 1995, 43(2): 1493-1504. |
| [17] |
LONG C S, CHUGG K M, POLYDOROS A. Further results in likelihood classification of QAM signals[C]// Military Communications Conference, Milcom '94. Conference Record. IEEE, 1994: 57−61.
|
| [18] |
 2022, Vol. 44
2022, Vol. 44
