0 引　言

岸电是指船舶在停靠港口码头期间，停止使用船舶上的发电机进行供电，采用港区码头上的岸电，通过电缆、接电箱等连接装备对船舶上工作设备、生活设备等进行供电。港口岸电供电技术对节能减排、建设绿色港口有着非常重要的意义，是解决靠港码头污染的重要举措^[1-2]。

传统并网控制策略有P/Q控制、V/F控制和下垂控制，但上述3种方法控制精度不高，且在并网过程中，岸电电源参数会出现剧烈波动^[3]。随着船舶岸电系统的使用范围越来越广，虚拟同步发电机控制技术应运而生并且成为逆变器控制的研究热点之一。VSG控制策略是在传统的控制方法上增加了惯性控制和阻尼控制^[4]，通过调节惯性和阻尼来抑制电压、频率、功率的波动，从而提高岸电电源的供电质量。

文献[5]根据同步发电机的数学原理，搭建了VSG控制模型，分析该模型相比于传统模型对系统电压、频率、功率稳定的影响并给出了优化方法。文献[6-7]推导了VSG的精确模型，分析了VSG控制模型同步频率谐振现象的产生机理及造成的不利影响，并提出有效的频率抑制策略。文献[8-9]提出了基于VSG控制的阻尼改进方法，抑制频率扰动，使VSG频率平稳输出，但对功率的调节较差。

根据以上文献研究发现，主要改进VSG控制中转子运动方程抑制频率扰动，但是对系统的输出功率调节较差，系统有功功率输出容易受到外部参数变化的影响，而且转子控制具有固定不变的转动惯量。系统在负载功率变化的过程中，频率发生扰动且自身无法调节，为了能够让频率在安全规范允许的范围内同时缩短调节时间，提出一种二次反馈调节的VSG控制策略。以有功频率控制器为基础，在有功频率控制器上增加角速度反馈调节，抑制功率变化。同时，在转子运动控制器上增加二次的转动惯量反馈调节来稳定频率，在系统负载变化时，能够快速地使系统达到稳定。

1 VSG岸电并网控制器 1.1 VSG组成及其原理

基于VSG的岸电并网控制模型如图1所示，其主电路为三相全桥逆变电路， $ {L_{fi}} $ 和 $ {C_{fi}} $ ( $ i= a，b，c $ )分别为滤波电感和电容， $ {r_i} $ 为滤波电感、开关器件、线路等元件的等效电阻之和； $ P $ ， $ Q $ ， $ f $ ， $ U $ 分别为输出侧的有功功率、无功功率、频率、电压幅值， $ {u^ * } $ 为 SVPWM控制算法的指令电压。

不同阶次的同步发电机模型可以建立不同的VSG的数学模型，从而达到不同的控制效果，但是3阶、5阶等高阶次的同步发电机建模比较复杂且实用价值低。因此，本文以2阶同步发电机建立VSG数学模型，VSG算法模块采用同步发电机的机电暂态数学模型，能够有效地模拟同步发电机的转子机械特性和定子电气特性。

VSG控制算法如下：

$ \left\{ {\begin{array}{*{20}{l}} {J\dfrac{{{\rm{d}}\Delta \omega }}{{{\rm{d}}t}} = {T_m} - {T_e} - D\Delta \omega } ，\\ {\dfrac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = \omega } ，\\ {{T_m} = \dfrac{{{P_m}}}{\omega },{T_e} = \dfrac{{{P_e}}}{\omega }} 。\end{array}} \right. $

(1)

式中： $ {T_m} $ 为机械转矩； $ {T_e} $ 为电磁转矩； $ {P_m} $ 为机械功率； $ {P_e} $ 为电磁功率； $ D $ 为定常阻尼系数； $ \Delta \omega = \omega - $ $ {\omega _0} $ 为角速度差， $ {\omega _0} $ 为额定角速度， $ \omega $ 为实际角速度；令极对数为1，则机械角速度 $ {\omega _m} = \omega $ ； $ \theta $ 为电角度。

VSG定子电磁方程为：

$ {E_{0i}} = {U_i} + {I_i}({r_a} + j{x_t}) 。$

(2)

式中： $ {E_{0i}} $ 为 $ i $ 相感应电动势； $ {U_i} $ 为 $ i $ 相定子端电压； $ {I_i} $ 为 $ i $ 相定子电流； $ {r_a} $ 为定子电枢电阻； $ {x_t} $ 为同步电抗。

图1中，岸电电源输出的有功功率给定值 $ {P_{{{re}}f}} $ 和频率的给定值 $ {f_{{{re}}f}} $ 经虚拟调速系统得到机械功率 $ {P_m} $ ，岸电电源输出的无功功率给定值 $ {Q_{{{re}}f}} $ 和电压给定值 $ {U_{{{re}}f}} $ 经虚拟励磁系统得到输出电压值 $ E $ 。将得到的 $ {P_m} $ 输入到虚拟同步发电机的转子控制器，得到频率 $ f $ ；再将 $ E $ 和 $ f $ 输入到电压电流双闭环控制器中，得到的 $ {u^*} $ 作为逆变电源的调节电压。

1.2 VSG控制器设计

VSG控制器包括有功频率控制器和无功电压控制器2个部分。

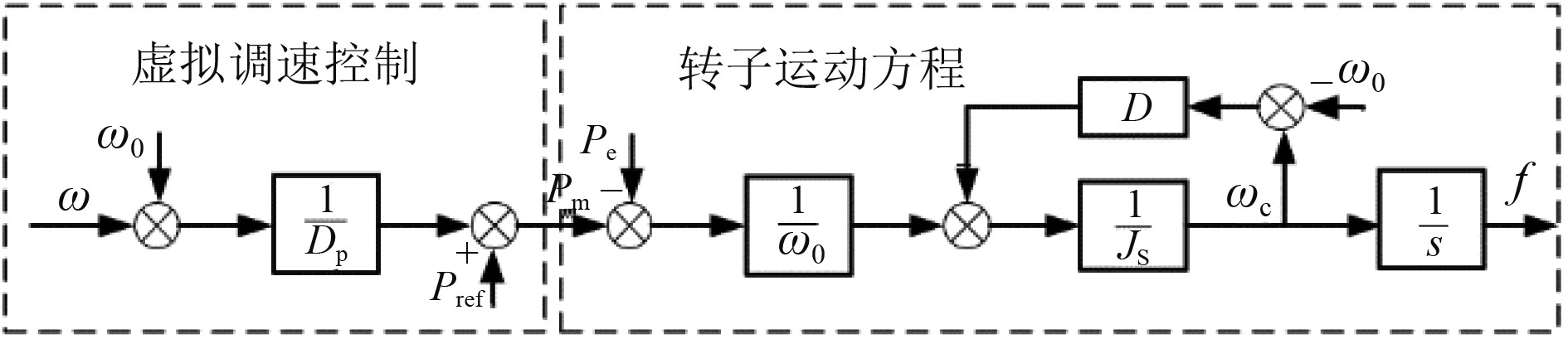
有功频率控制器主要包括有功功率控制器和转子运动控制器，使控制器具有惯性和阻尼特性，控制框图如图2所示。

图中， $ {D_p} $ 为调节系数， $ {P_m} $ 为机械功率， $ {P_e} $ 为输出有功功率， $ \omega $ 为输出角频率， $ {\omega _0} $ 为角频率参考值， $ J $ 和 $ D $ 分别为虚拟惯量和阻尼系数。

将无功功率给定值 $ {Q_{ref}} $ 和无功功率 $ Q $ 的偏差值通过无功调节后，与输出电压给定值 $ {U_{ref}} $ 和输出电压 $ U $ 调节后的偏差值共同组成励磁调节控制器，其控制框图如图3所示。

图中， $ {D_q} $ 为无功调节系数， $ {K_u} $ 为电压调节系数。

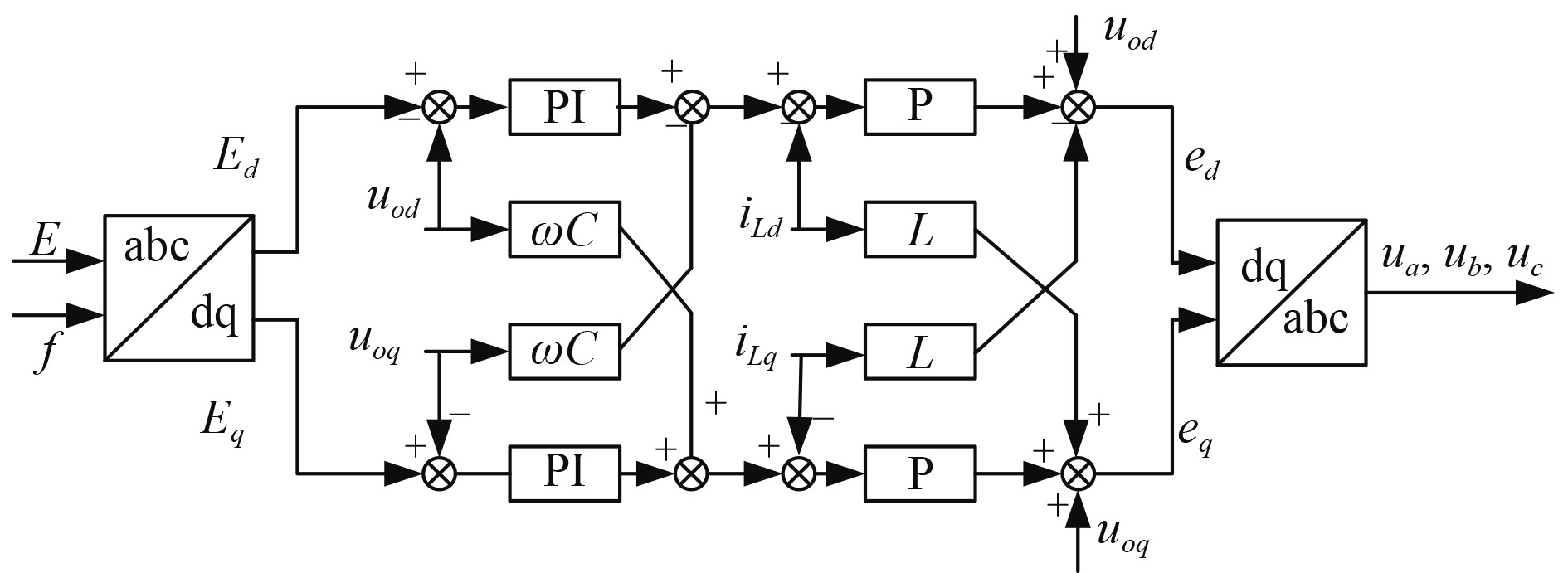
为了能及时匹配岸电并网控制系统的给定值，保证控制性能，在设计电压电流双闭环控制时，根据系统控制特性设计，外环设计为电容电压的PI控制，内环为电感电流的P控制，控制框图如图4所示。

图中， $ E $ 和 $ f $ 为虚拟同步发电机输出的电压和频率。

2 改进的VSG控制算法

在传统下垂控制中，船舶岸电并网系统控制良好，但由于其本身为阶跃函数的特性，无法满足逆变器对并网系统的快速响应^[10]，在预同步切换及负荷功率发生变化时，对船舶电网的频率影响比较大。为了实现岸电并网系统的频率稳定运行，对VSG控制算法中的有功频率控制器环节进行改进。

船舶柴油同步发电机的2阶机电暂态模型为：

$ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\rm{d}}\delta }}{{{\rm{d}}t}} = \left( {{\omega _J} - 1} \right){\omega _{J0}}} ，\\ {{T_J}\dfrac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = {P_m} - {P_e} - D\left( {{\omega _J} - 1} \right)} 。\end{array}} \right. $

(3)

式中： $ \delta $ 为角位移； $ {\omega _J} $ 为柴油发电机转速； $ {\omega _{J0}} $ 为柴油发电机额定转速； $ {T_J} $ 为惯性时间常数。

当柴油发电机的有功增量为 $ \Delta P $ 时，则角速度增量为：

$ \Delta {\omega _J} = \left( {\Delta P/D} \right)\left( {1 - {e^{ - {T_J}t/D}}} \right) 。$

(4)

可知：系统在切换过程中，角速度的变化由惯性时间 $ {T_J} $ 和阻尼系数 $ D $ 控制，由于系统的惯性比较足，所以能使系统频率保持稳定。

由下垂控制原理可知，有功功率的功率方程为：

$ P = {P_{ref}} + {K_p}\left( {\omega - {\omega _0}} \right) 。$

(5)

式中： $ P $ 为有功功率输出值； $ {P_{ref}} $ 为有功功率给定值； $ {K_p} $ 为调节系数； $ {\omega _0} $ 为额定角速度； $ \omega $ 为实际角速度。

由式（1）、式（3）、式（5）得有功功率控制方程的角速度增量和有功功率增量闭环传递函数为：

$ \frac{{\Delta \omega }}{{\Delta P}} = \frac{{\omega - {\omega _0}}}{{P - {P_0}}} = - \frac{{{K_p}}}{{{K_p}{T_J}s + {K_p}D + 1}} = - \frac{{{K_L}}}{{{T_J}^{'}s + 1}} 。$

(6)

式中： $ {T}_{J}{}{\text{′}}={K}_{p}{T}_{J}/（{K}_{p}D\text{+}1） $ 为惯性时间常数； $ {K}_{L}= $ $ {K}_{p}/（{K}_{p}D+1） $ 为调差系数。

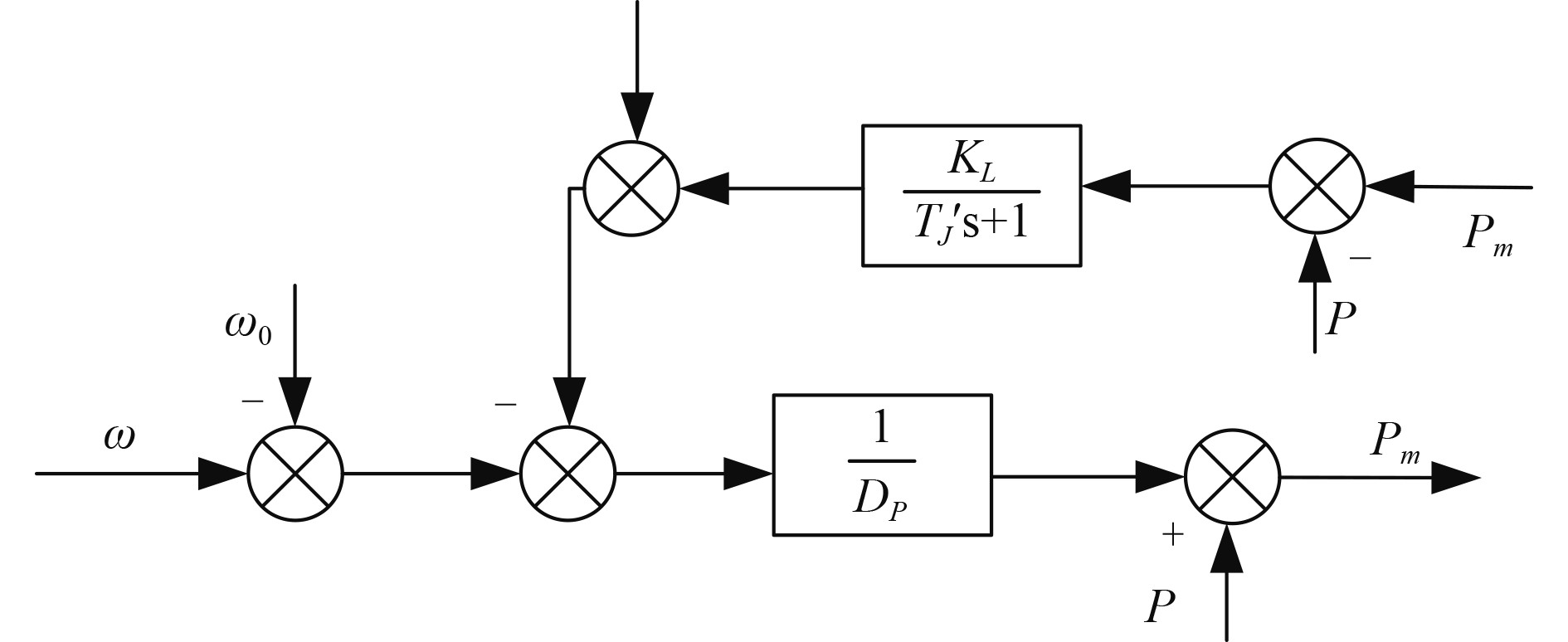
因此有功功率控制框图可改进为如图5所示。

转动惯量 $ J $ 的大小与转子系统所储存的动能容量有着密切的联系，同时转子系统的动能容量对控制系统的暂态过程有影响，所以当并网控制系统出现参数扰动时，调节转动惯量 $ J $ 可以迅速使系统恢复稳定^[11]。通常情况下，VSG控制算法拥有固定的转动惯量，无法满足自动调节条件。

VSG中有功功率、无功功率为：

$ \left\{ {\begin{array}{*{20}{c}} {P = \dfrac{{{E_e}U}}{Z}\cos (\theta - \delta ) - \dfrac{{{U^2}}}{Z}\cos \theta }，\\ {Q = \dfrac{{{E_e}U}}{Z}\sin (\theta - \delta ) - \dfrac{{{U^2}}}{Z}\sin \theta } 。\end{array}} \right. $

(7)

式中： $ {E_e} $ 为线电压有效值； $ Z = \sqrt {{{(\omega L)}^2} + {R^2}} $ 为滤波阻抗； $ \theta = \arctan ({{\omega L} \mathord{\left/ {\vphantom {{\omega L} R}} \right. } R}) $ 为阻抗角； $ L $ 为电感； $ R $ 为电阻。

VSG的有功功率输入、输出传递函数为：

$ G\left(s\right)=\frac{P\left(s\right)}{{P}_{ref}（s）} = \frac{U{U}_{g}/J{\omega }_{0}Z}{{s}^{2}+\left(D/J+{K}_{\omega }/J{\omega }_{0}\right)s+U{U}_{g}/J{\omega }_{0}Z} 。$

(8)

式中： $ U $ 为VSG输出电压； $ {U_g} $ 为发电机输出电压； $ {K_\omega } $ 为VSG的有功功率调差系数。

根据式（8）传递函数可得自然震荡角 $ {\omega _n} $ 和阻尼系数 $ \varepsilon $ 。

$ \left\{ {\begin{array}{*{20}{l}} {{\omega _n} = \sqrt {\dfrac{{U{U_g}}}{{J{\omega _0}Z}}} }，\\ {\varepsilon = \dfrac{D}{2}\sqrt {\dfrac{{U{U_g}}}{{J{\omega _0}Z}}} + \dfrac{{{K_\omega }}}{2}\sqrt {\dfrac{Z}{{J{\omega _0}U{U_g}}}} } 。\end{array}} \right. $

(9)

当0< $\varepsilon $ <1，误差允许范围±2%，调节时间和超调量 $\sigma $ 分别为：

$ \left\{ {\begin{array}{*{20}{l}} {{t_s} = \dfrac{4}{{\varepsilon {\omega _n}}}} ，\\ {\sigma = {e^{\frac{{ - {\text{π}} \varepsilon }}{{\sqrt {1 - {\varepsilon ^2}} }}}} \times 100\% } 。\end{array}} \right. $

(10)

可知，当 $D$ 和 ${K_\omega }$ 为恒定值时，若 $J$ 增大， $\varepsilon $ 便减小， $\sigma $ 变大， ${t_s}$ 亦增加。

由图2可知，有功功率控制方程可以表示为：

$ \frac{1}{{Js}}\left[ {\frac{1}{{{\omega _0}}}\left[ {\frac{1}{{{D_p}}}\left( {\omega - {\omega _0}} \right) + {P_{ref}} - {P_e}} \right] + D\left( {{\omega _c} - {\omega _0}} \right)} \right] = {\omega _c} 。$

(11)

同理，结合式（5）和式（11）得到角速度增量和有功功率增量闭环传递函数为：

$ \frac{{\Delta \omega }}{{\Delta P}} = \frac{{{\omega _c} - {\omega _0}}}{{P - {P_0}}} = - \frac{1}{{J{\omega _0}s + D{\omega _0} + {K_P}}} = - \frac{{{D_P}}}{{{T_J}^*s + 1}} 。$

(12)

式中， $ {T}_{J}{}^{*}=J{\omega }_{0}/（D{\omega }_{0}+{K}_{P}） $ 为转动惯量调节系数， $ {D}_{P}=1/（D{\omega }_{0}+{K}_{P}） $ 为有功功率下垂系数。

当阻尼系数 $ D $ 为定值时，转动惯量调节系数 $ {T_J}^* $ 随 $ J $ 变化而变化。故引入转动惯量调节控制，其控制方程为：

$ \left\{\begin{array}{l} J={J}_{0}+{K}_{f}\Delta f+{K}_{\omega }\Delta \omega ,\Delta f > k,\Delta \omega > k，\hfill \\ \Delta f=f-{f}_{0}\text{，}\begin{array}{ccc} \end{array}{f}_{0}{\scriptsize{为初始频率}}，\hfill \\ \Delta \omega =\omega -{\omega }_{0}\text{，}\begin{array}{ccc} \end{array}{\omega }_{0}{\scriptsize{为初始角速度}}。\hfill \end{array} \right.$

(13)

式中： $ {K_f} $ 为频率调节系数； $ {K_\omega } $ 为角速度调节系数； $ k $ 为变化量限定值； $ {J_0} $ 为转动惯量初始值。

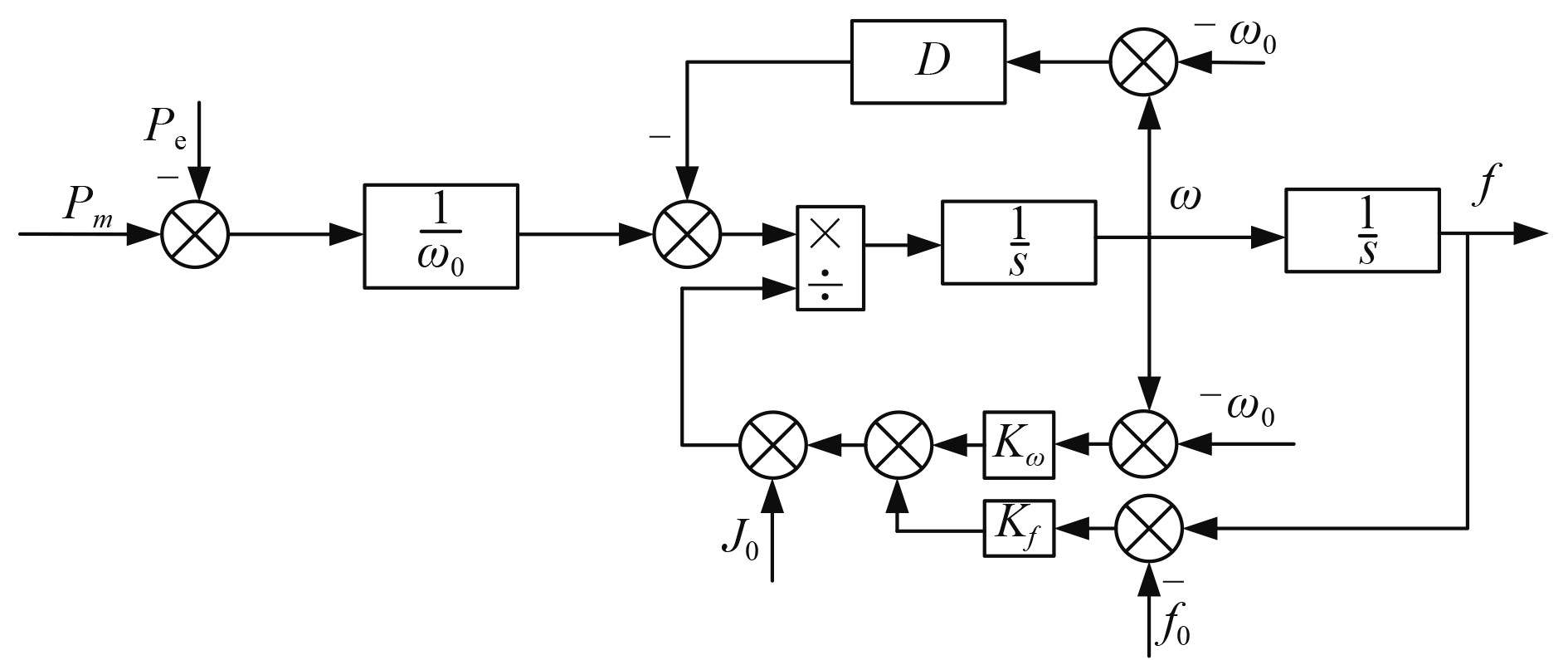
VSG控制策略中改进的转子控制结构框图如图6所示。

图中，在岸电并网系统开始运行时，将初始的转动惯量值 $ {J_0} $ 设置为较小值，降低其过大引起并网系统功率振荡的可能性；在负载功率切换过程中，频率、功率等参数容易发生扰动，此时系统采用转动惯量调节控制，可以有效抑制频率和功率的迅速上升和跌落问题，提高船舶岸电并网系统稳定。

3 仿真分析

以400 V/50 Hz的低压船舶为例，设计低压岸电电源与船舶电网的并网控制模型，采用上述改进的VSG控制策略对逆变器电源进行控制，利用Matlab/Simulink仿真软件建立图1所示的控制模型。系统开始运行时，采集模块采集逆变器输出电压、电流等参数，经功率模块、控制模块、电压电流双闭环模块产生控制信号，完成系统的整体运行。仿真参数如表1所示。

根据船舶并网规范要求，岸电系统的三相输出电压允许的偏差应为 $ \pm 5{\text{% }}$ ；频率波动的允许偏差值应为 $ \pm 2{\text{% }}$ ；负载功率变化的最大值不应超过为 $ \pm 30{\text{% }}$ 。当负载变化数据小于最大值时，冲击电压、冲击电流、频率扰动、功率变化均小于最大值。故本文选择负载功率逐步变化至最大值作为仿真数据，通过分析电压、电流、频率、功率等参数变化，验证所提改进控制策略的有效性。

3.1 转动惯量验证

在VSG并网控制模型中，验证转动惯量对频率的影响。仿真过程参数设置：0～0.1 s，预同步时间；0.1～0.5 s，系统带负载运行；在0.5 s时，增加系统30%负载功率；在0.8 s时，减少系统30%的负载功率；0.8～1 s，系统恢复稳定。

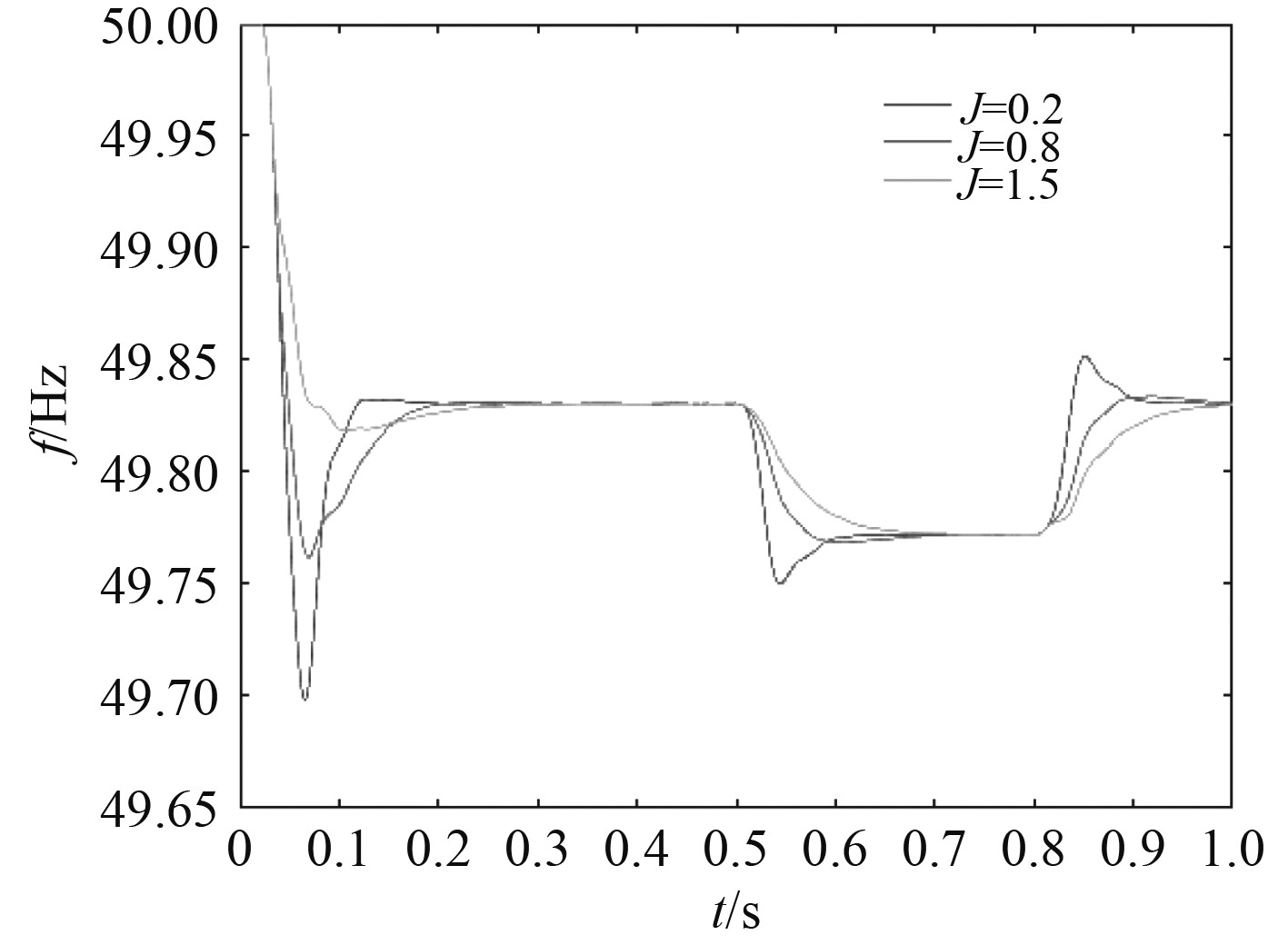
不同的转动惯量对频率的影响如图7所示。在系统负载功率变化时，不同的转动惯量 $ J $ 对频率变化的影响不同，不同的转动惯量 $ J $ 对系统调节时间也不同，因此，可以通过调节转动惯量 $ J $ 来提高并网控制系统的频率稳定。

3.2 改进VSG的并网控制仿真分析

仿真过程参数设置：岸电系统启动，0～0.1 s预同步时间；0.1～0.3 s时，岸电电网带负载运行，岸侧电源单独运行；在0.3 s时，增加5%的负载功率；在0.5 s时，系统再次增加10%的负载功率；在0.7 s时，系统再次增加15%的负载功率；在0.8 s时，系统切除船舶负载功率；0.8～1 s，系统再次恢复稳定。

1）并网及负载功率变化的控制仿真

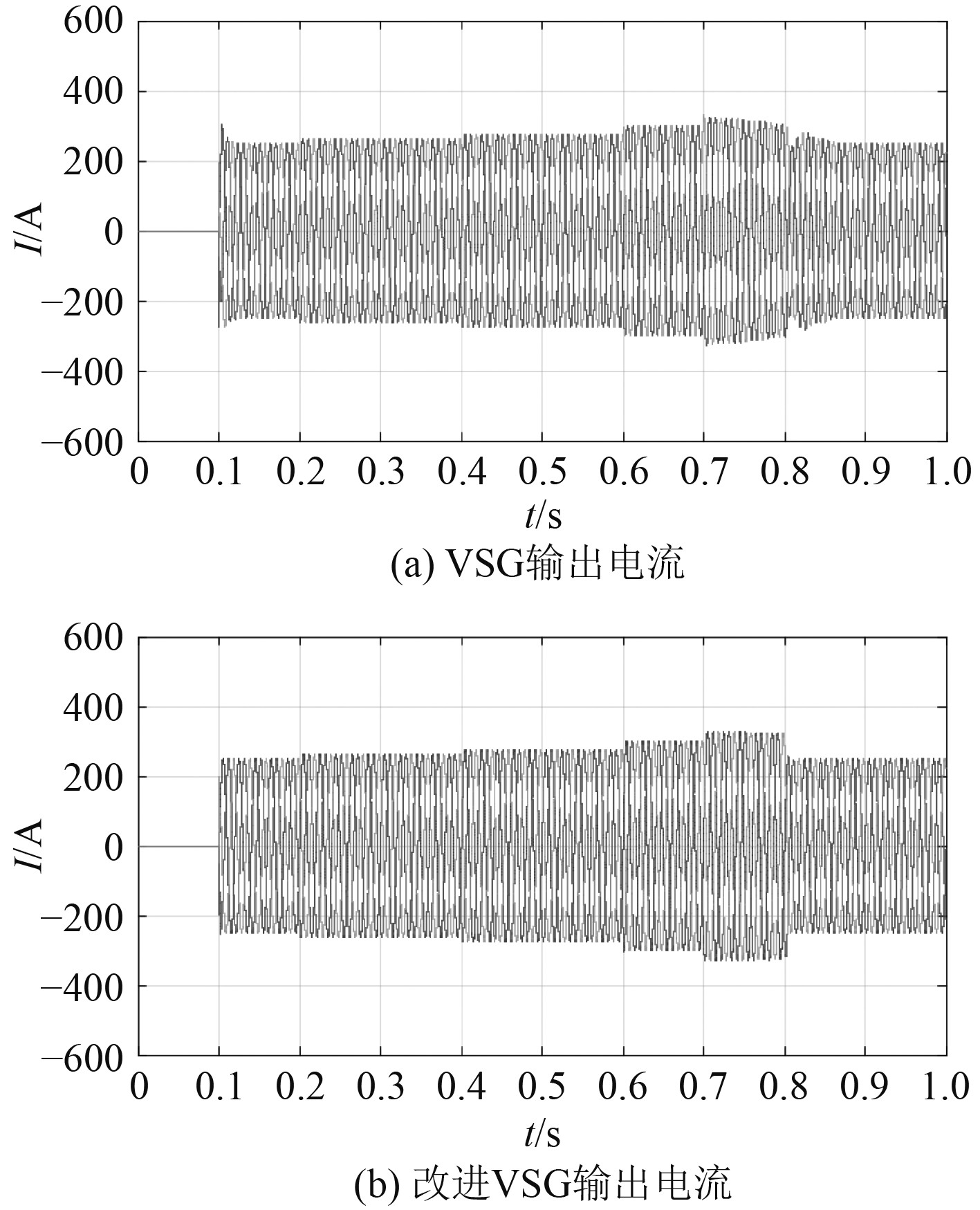
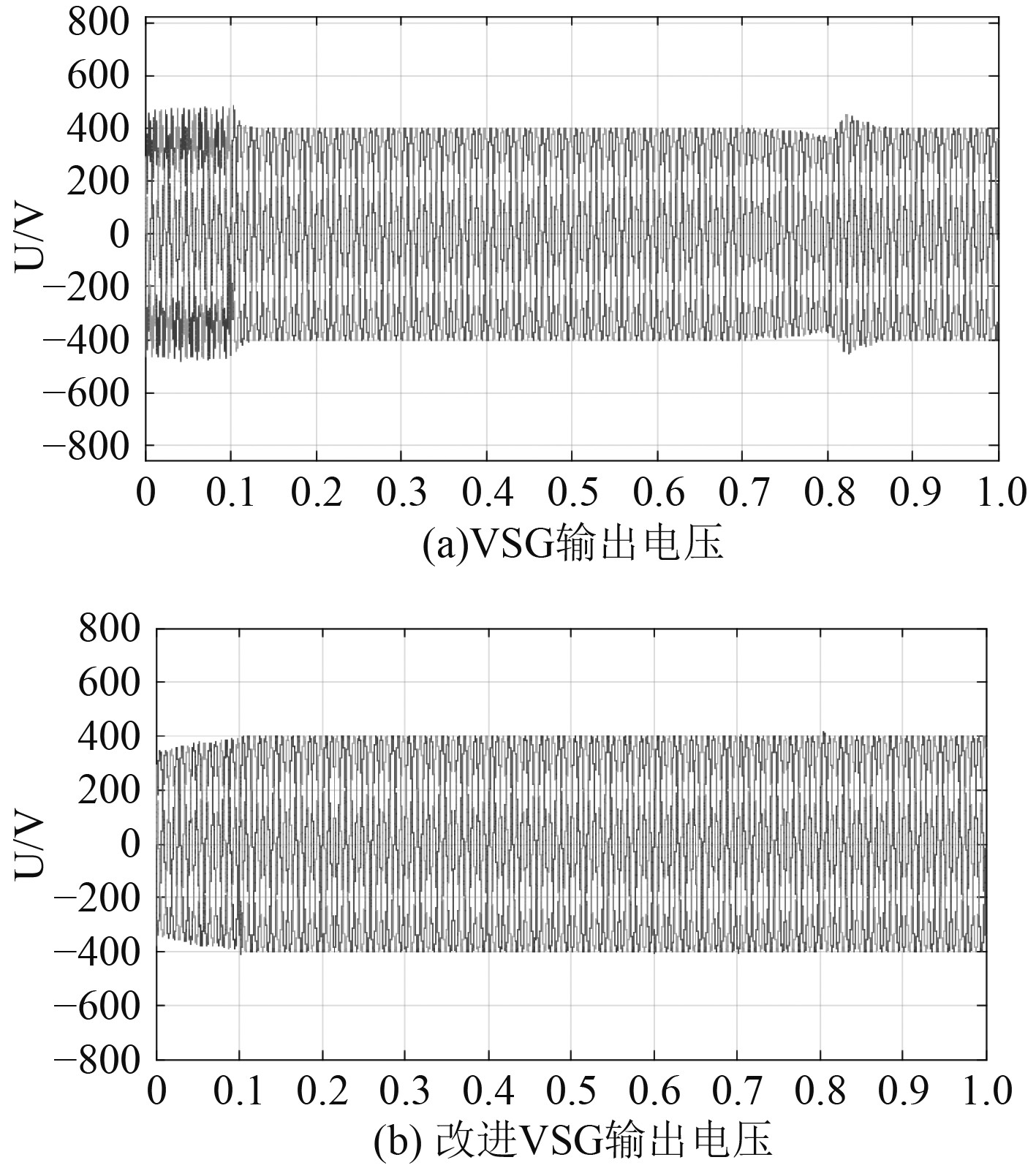
由图8和图9可知，在预同步期间，VSG控制的岸侧输出电压出现波动且电压增大至470 V左右，在切换时出现的跃变电流值为300 A左右。

在逐步增加负载功率时，输出电压保持稳定，电流迅速增加并缓慢衰退至稳定；在0.8 s减少30%的负载功率时，电压再次波动至450 V左右，电流出现畸形。

在改进VSG 控制中，预同步期间，电压缓慢增加至额定电压，电流无跃变。

在逐步增加负载功率时，最大跃变电压为404.5 V；在0.8 s减少30%的负载功率时，最大跃变电压为413.5 V，电流平滑切换，满足岸电并网电压规定的 $ \pm 5{\text{% }}$ 的标准。

2）并网及负载功率变化的频率调节仿真

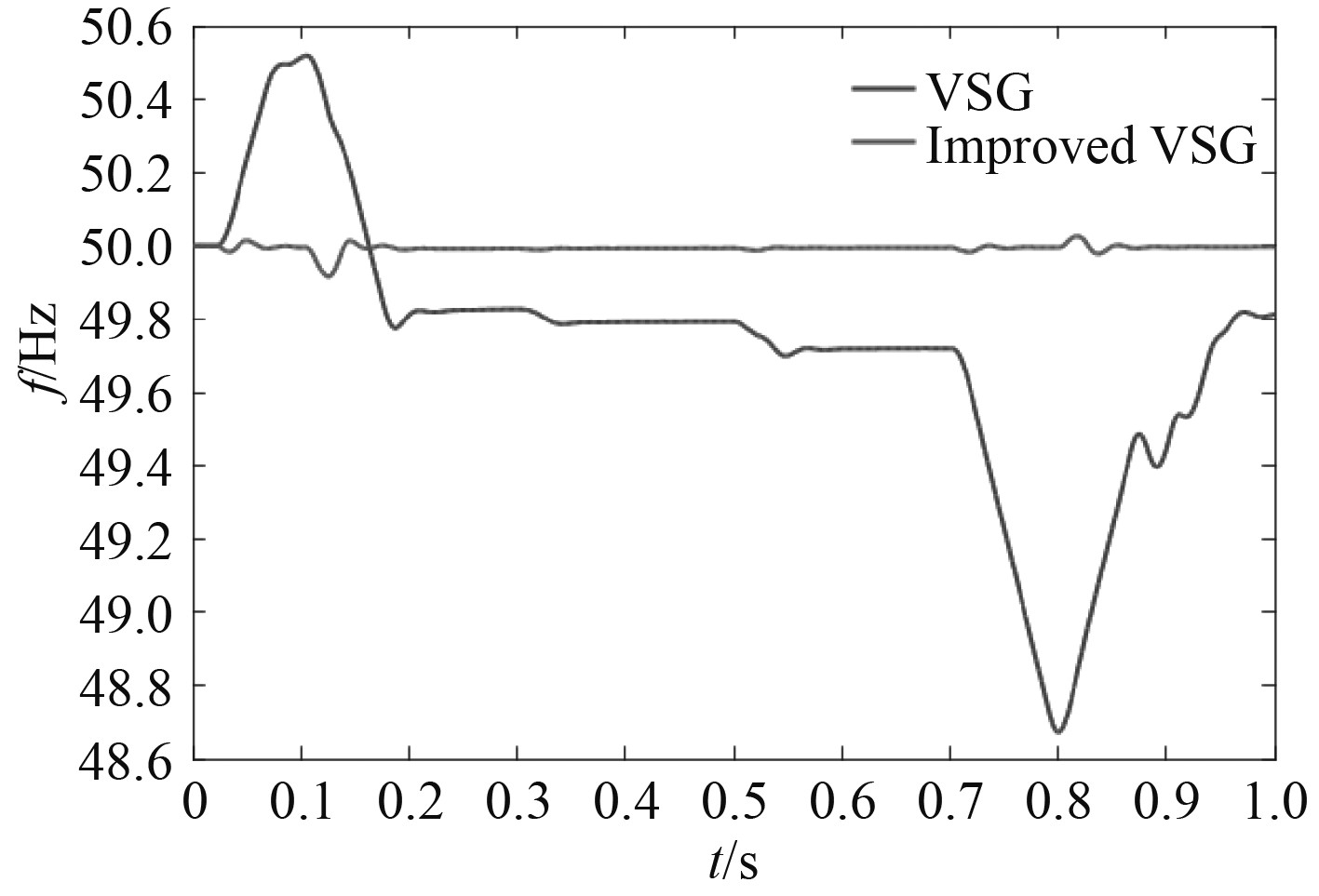
如图10所示，VSG与改进VSG的输出频率对比图，当系统开始运行时，在预同步期间，VSG控制算法的逆变器输出频率迅速上升，且当增加或减少负载功率时，系统频率会出现较大的波动，且无法自动调节使频率维持稳定。

而采用改进VSG控制算法，在预同步期间能够有效地抑制频率变化，当系统负载功率发生变化时，也能够快速恢复平稳状态，控制精度更接近电网给定频率。同时，满足岸电并网频率规定的 $ \pm 2{\text{% }}$ 的标准。

根据图10可得到频率在各时间变化的具体数值如表2所示。

3）并网及负载功率变化的输出功率仿真

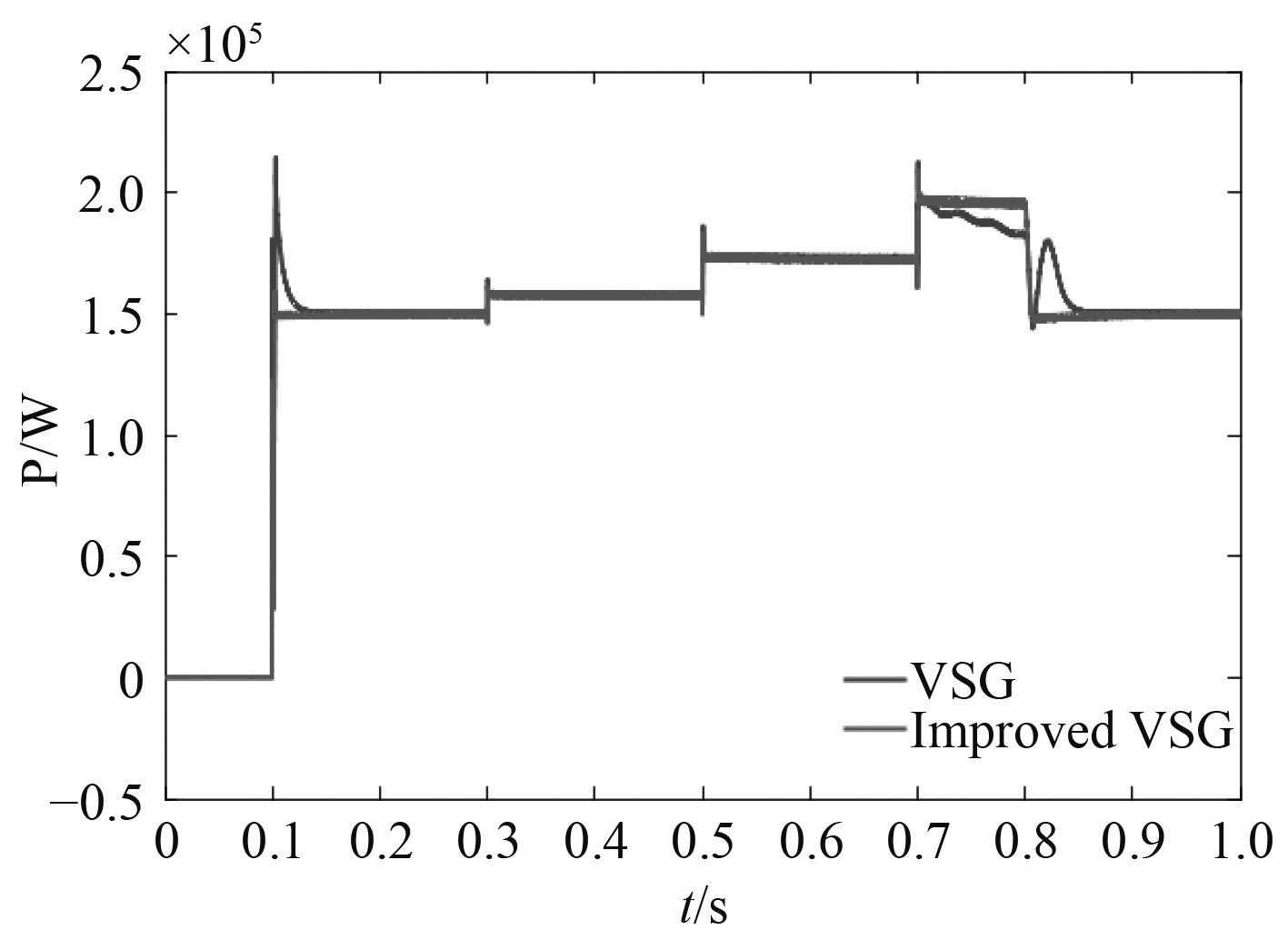
由图11可知，在船舶岸电并网系统仿真中，VSG控制在预同步结束后即0.1 s接入负载时，功率增至214.4 kW，然后缓慢跌落至给定功率。在0.3 s时，增加5%的负载功率，输出有功功率增至164.1 kW；0.5 s时，增加10%的负载功率，输出有功功率增至186.4 kW；0.7 s，增加15%的负载功率，输出有功功率增至212.5 kW而且出现输出功率不稳定现象，在0.8 s时，跌落至182.5 kW。在0.8 s减少30%的负载功率时，功率波动至180.1 kW，在0.86 s系统趋向稳定值。

与VSG控制输出有功功率相比，改进VSG控制输出功率在增加或切除负载功率时，波形浮动较小，系统到达稳定的反应时间更加迅速。

4 结　语

本文针对船舶岸电并网控制系统预同步切换及负载功率变化的过程中，冲击电压、冲击电流过大及频率扰动等问题，研究基于VSG的逆变器控制策略，阐述了VSG控制算法的基本原理及其模型建立，分析VSG控制算法中对系统频率扰动的因素，针对参数扰动问题，提出了一种二次反馈调节的VSG控制策略。在保证岸电系统能够平滑切换的基础上，通过对有功功率控制器和转子运动控制器的改进来抑制预同步切换及负载功率发生变化时系统电压、电流、频率和功率的波动。最后，通过仿真验证了所提策略的有效性和可行性。