0 引　言

现代水下攻防战中，各国海军对水下航行器的重视程度越来越高。当水下航行器航行时，其内部布置压载水舱的液体由于惯性会产生晃荡，严重情况下会影响航行器的稳定性。液体晃荡的定义从广义范围上讲是指容器内介质（主要为液体）的自由变化。计算液体晃荡的关键问题在于如何精准确定自由液面位置，至今学者们已经提出几种有效的描述方法，例如波高函数法、MAC法、VOF法、Level-set法及SPH法等。其中VOF法因能对自由液面进行精确捕捉，并能够和各种离散方法并行计算，成为处理自由液面问题的有效途径。

Abramson^[1]分析了多种不同类型液舱内的液体运动，研究各个参数对液面晃荡造成的响应。Faltinsen^[2]构造了自由液面在矩形液舱内液体遭受外部（主要为余弦）激励的线性解析解，并拓展为同形状容器中自由液面晃荡问题的非线性解析解^[3]，其研究成果被Faltinsen等^[4]深层次应用于数值模拟更加典型的非线性计算。Cho等^[5]模拟了受外部水平激励时矩形液舱的剧烈振荡。Wang等^[6]对随机激励下液面的非线性水动力系数进行了计算。Liu^[7]选取创新的数值模型去研究计算存在不完整自由液面的非线性晃荡。Lu^[8]耗费了较长时间模拟液舱晃荡，从而得到较为收敛的数值计算结果，并简单阐述了能量耗散的原理。近年来数值模拟^[9]的方法在不断升级进步，也出现了一些无网格化的方法，但采用大型商用软件针对晃荡问题进行的研究不多，为研究大型商用软件对晃荡问题的模拟能力及可靠性，本文采用STAR-CCM+软件建立2种不同形状的二维水平液舱模型，数值模拟外部余弦激励下的自由液面晃荡，其结果对评估水下航行器的稳定性具有借鉴意义。

1 晃荡问题的数值方法 1.1 条件假设

某水下航行器主压载水舱轴向与航行器轴向垂直，因此液舱的晃荡对航行器横倾平衡影响较大，且航行器横倾平衡的调节手段较少。为方便未来研究液舱晃荡对航行器航行时姿态的影响，采用以下假设：

1）航行器稳定直航；

2）液面不可压缩，且为黏性流；

3）液舱不在冲击载荷作用下发生变形。

1.2 VOF法基本原理

在不可压缩假定下，液舱内流体运动满足Navier-Stockes雷诺平均方程（RANS方程）：

$ \frac{{\partial \rho {u_i}}}{{\partial {x_i}}} = 0 ，$

(1)

$ \frac{{\partial \rho {u_i}}}{{\partial t}} + \frac{{\partial \rho \left( {{u_j} - u_j^m} \right){u_i}}}{{\partial {x_j}}} = \rho {f_i} - \frac{{\partial p}}{{\partial {x_i}}} + \rho v\frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)。$

(2)

式中： $\rho $ 为舱内液体的密度， ${u_i}$ 为 $i$ 方向的速度分量， $t$ 为时间。 ${f_i}$ 为单位体积流体所受到的体积力。

VOF(volume of fluid)方法是一种典型的界面追踪方法，它建立在欧拉网格的基础之上。该方法选取流体体积分数为界面函数 $F$ （在多相流中，称色函数，用 $C$ 表示） 这一变量来实现对计算域内相间界面的追踪。

$F$ 满足方程 $\dfrac{{{\rm{d}}F}}{{{\rm{d}}t}} = 0$ ，结合连续方程，则 $F$ 应满足

$ \frac{\partial }{{\partial t}}\left( {\theta F} \right) + \frac{\partial }{{\partial x}}\left( {\theta uF} \right) + \frac{\partial }{{\partial y}}\left( {\theta vF} \right) = 0。$

(3)

2 液舱晃荡数值模型建立和验证

在开展数值模拟计算之前，通过对比数值模拟计算和Faltinsen解析解的结果，证明数值模拟的准确性。

2.1 仿真流程和计算参数设置

仿真流程如图1所示，计算参数设置如表1所示。

2.2 二维水平液舱模型及液体晃荡固有频率分析 2.2.1 二维水平液舱模型

选取位于某水下航行器中部的水平圆柱体压载水舱，水舱三维尺寸长×宽×高=1 185 mm×855 mm×855 mm，简化为二维半圆-矩形液舱模型^[10]，如图2所示。二维主压载水舱模型的构建采用CATIA软件，网格划分及数值模拟计算均在STAR-CCM+软件中进行，选取四边形结构化的网格划分形式。为了提高流场的流体特征分辨率，对自由液面附近区域采取了网格加密处理，模型生成的网格数目约为8万。

2.2.2 液体晃荡固有频率分析

在时间步长的设定和压力函数的选取上，VOF模型的计算时间步长的设置应尽量小一些。本文设置时间步长为0.001 s，时间步数为5000，最大迭代步长为50。

当外部给定频率接近或达到液舱的固有频率时，晃荡最为剧烈。液舱系统固有频率理论计算已验证的公式为：

$ {\omega _i} = \sqrt {g{k_n}\tanh {k_n}d},\;\; n = 0,1,2 \cdot \cdot \cdot ,{k_n} = (2n + 1){\text{π}} /L 。$

(4)

Faltinsen^[2]构造了势流解析解，给定水平液舱遭受一个外部激励： ${u_e} = - A\cos \omega t$ 。

式中： ${u_e}$ 为液舱激励速度函数； $A = b\omega $ 为速度幅值； $b$ 为激励幅值； $\omega $ 为激励频率。由速度势函数 $\phi $ ，根据解析解，易得自由液面的位移 $\eta = \dfrac{1}{g}{\dfrac{{\partial \phi }}{{\partial t}}_{z = 0}} 。$

$ \begin{split} \eta =& \frac{1}{g}\sum\limits_{n = 0}^\infty {\sin \left[ {\frac{{(2n + 1){\text{π}} }}{{2a}}x} \right]} \cosh \left[ {\frac{{(2n + 1){\text{π}} }}{{2a}}h} \right]\times\\ &\left( { - {A_n}{\omega _n}\sin {\omega _n} - {C_n}\omega \sin \omega t} \right)- \frac{1}{g}A\omega x\sin \omega t，\end{split} $

(5)

$ \omega _n^2 = g\dfrac{{(2n + 1){\text{π}} }}{{2a}}\tanh \left[ {\dfrac{{(2n + 1){\text{π}} }}{{2a}}h} \right]，$

(6)

$ {A_n} = - {C_n} - \dfrac{{{K_n}}}{\omega }，{C_n} = \dfrac{{\omega {K_n}}}{{\omega _n^2 - {\omega ^2}}}，$

(7)

$ {K_n} = \frac{{\omega A}}{{\cosh \left[ {\dfrac{{(2n + 1){\text{π}} }}{{2a}}h} \right]}}\frac{2}{a}{\left[ {\dfrac{{2a}}{{(2n + 1){\text{π}}}}} \right]^2}{( - 1)^n}。$

(8)

根据固有频率分析计算得 ${\omega _0}$ =4 rad/s。

2.2.3 数值模拟可靠性验证

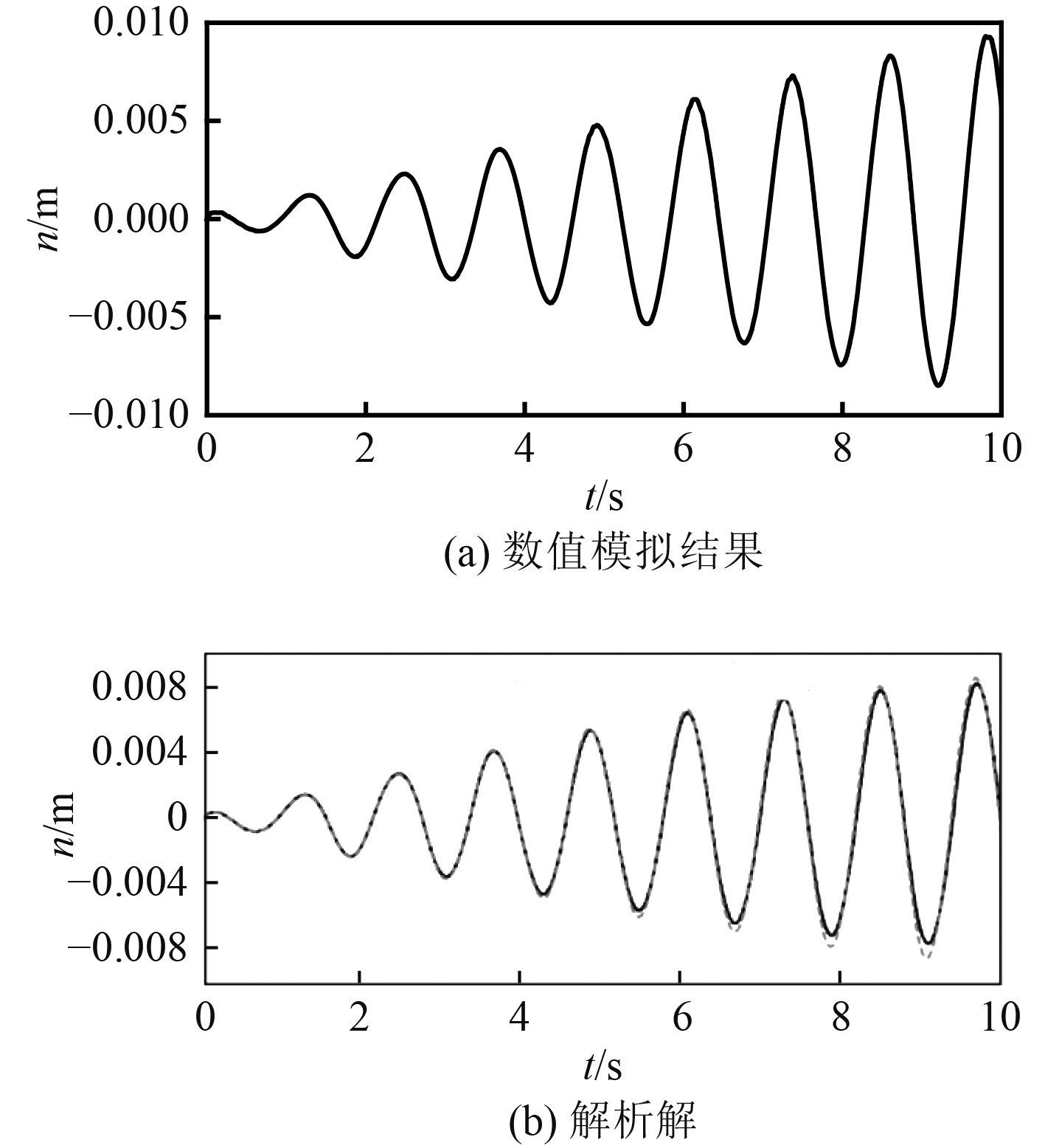
出于直观比较证明数值模拟结果精确性的目的，选取2种计算工况得到x=0.5 m处晃荡的波高历时曲线，如图3和图4所示。根据参考文献，验证选取的液舱模型尺寸为：L=2a=1.0 m，高H=1.0 m，液舱内静止水深h=0.5 m^[2]，计算得固有频率 ${\omega _0}$ =5.314 rad/s。

可知，在距离共振频率较远处的 $\omega $ =0.5 ${\omega _0}$ ，位移激励振幅b=0.01 m，和在距离共振频率较近处的 $\omega $ = 0.95 ${\omega _0}$ ，位移激励振幅b=0.0004下，数值模拟和解析解误差较小，这证明液舱晃荡的模型是可靠的。

图5为半圆-矩形液舱自由液面初始状态的云图，在自由液面和舱壁交界处下方0.05 m的point1设置一监测点监测壁面位置处压力的变化。

3 晃荡数值模拟 3.1 振幅工况对晃荡的影响

为对比不同形状液舱对激励振幅的响应，分别选用矩形和半圆-矩形液舱模型进行晃荡数值模拟。矩形液舱模型的长为118 5 mm，宽为855 mm，其液舱模型及其网格划分如图6所示。

选取矩形液舱模型，在外界激励频率 $\omega = 0.5\;{\omega _0}$ ， $\omega = {\omega _0}$ 时，考虑b=0.003 m和0.004 m不同位移振幅对液体晃荡的影响，监测其侧面一监测点的自由液面相对波高时历曲线（ $ \eta /b $ ），如图7所示。

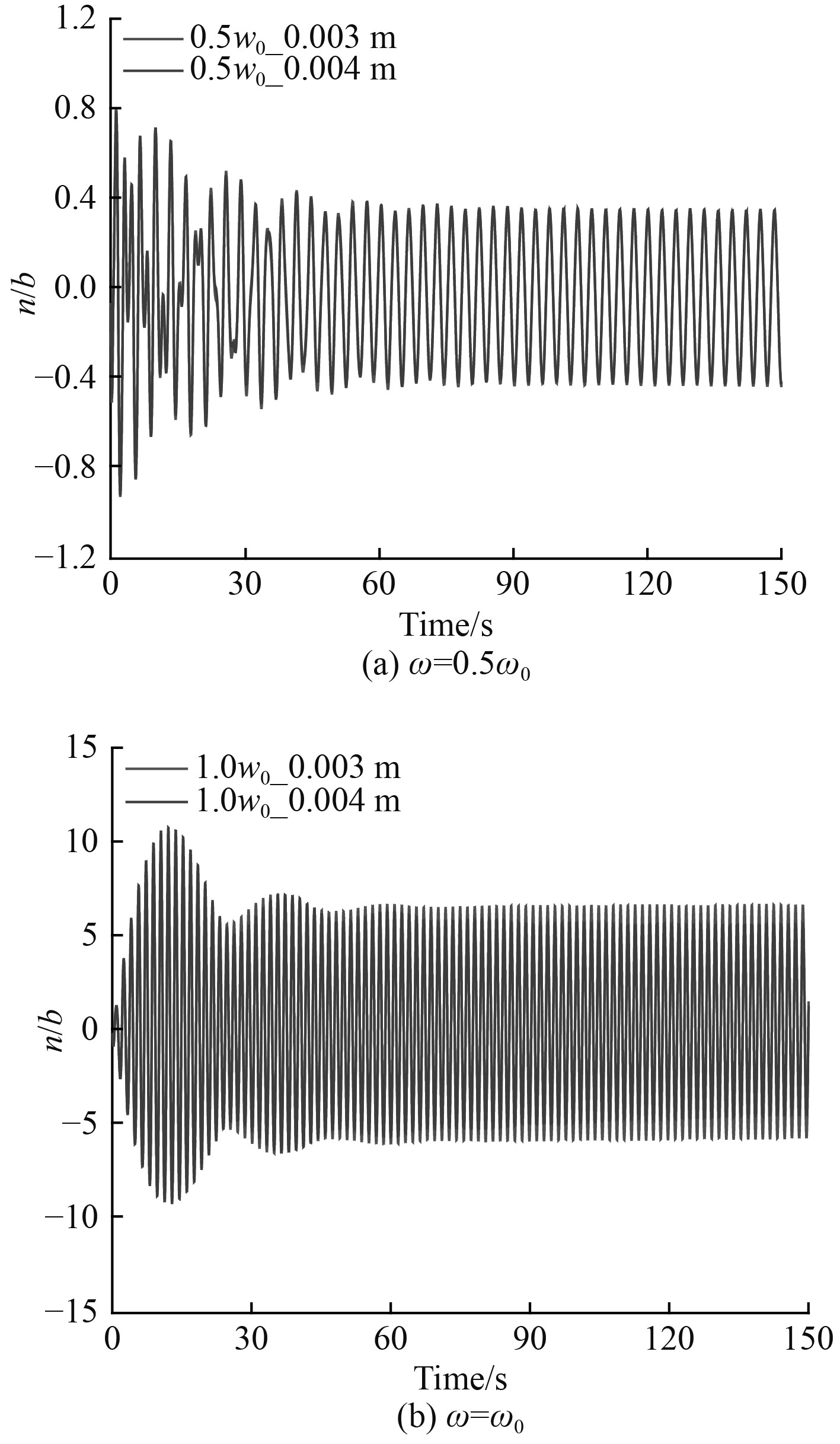
选取建立的半圆-矩形液舱模型，在外界激励频率 $\omega = 0.5\;{\omega _0}$ ， $\omega = {\omega _0}$ 时，考虑b=0.003 m和0.004 m不同位移振幅对液体晃荡的影响，监测其侧面一监测点的自由液面相对波高时历曲线（ $ \eta /b $ ），如图8所示。

可以看出，随着模拟时间的增加，在开始的30 s内，均呈现了明显的非线性现象，随后幅值趋于稳定。不同振幅的曲线差别较小，这证明该情况下施加的激励晃荡与线性相接近。对比矩形液舱模型和半圆-矩形液舱模型不同振幅下的波高历时曲线，半圆-矩形液舱模型波高波峰波谷差值略大，波动周期略长，二者的总体变化规律差别较小。

$\omega $ =0.5 ${\omega _0}$ 工况振幅为0.003 m和0.004 m时， $ \eta /b $ 值分别稳定在0.34和0.36； $\omega = {\omega _0}$ 工况振幅为0.003 m和0.004 m时， $ \eta /b $ 值分别稳定在6.58和5.67。在 $\omega $ =0.5 ${\omega _0}$ 工况下，随着振幅的增加 $ \eta /b $ 略微增加，增幅为5.9%；在 $\omega $ = ${\omega _0}$ 工况下，随着振幅的增加 $ \eta /b $ 略微减小，减幅为13.8%。

由图9可以看出，在位移振幅工况选取0.003 m和0.004 m的情况下，舱内液体晃荡的冲击会对舱壁施加压力，此压力有周期性规律。在开始的40 s内，呈现了明显的非线性现象，随后压力幅值达到平稳，趋于一个稳定的值。在80 s后，幅值略为减小，趋于一个新的稳定值。且随着激励振幅的增大，液舱晃荡对舱壁上一点压力的稳定波峰值增大而稳定波谷值减小，压力时历曲线变宽。

3.2 频率工况对晃荡的影响

选用半圆-矩形液舱模型，位移激励振幅b=0.003 m，选取频率为 $\omega $ =0.5 ${\omega _0}$ ，0.8 ${\omega _0}$ ，1.0 ${\omega _0}$ ，1.2 ${\omega _0}$ 和1.5 ${\omega _0}$ ，监测其侧面一监测点的波高/振幅，其不同频率下 $ \eta /b $ 值如图10所示。

如图10所示，在激励频率 $\omega $ =0.5 ${\omega _0}$ ，0.8 ${\omega _0}$ ，1.0 ${\omega _0}$ ，1.2 ${\omega _0}$ 和1.5 ${\omega _0}$ 工况下， $ \eta /b $ 值分别稳定在0.36，3.02，6.58，1.81和0.60，在固有频率附近 $ \eta /b $ 值达到最大，小于或大于固有频率工况时， $ \eta /b $ 值随着 $\omega $ 远离固有频率值而减小。

将不同频率下平稳后的波高分布值做成如图11所示不同频率自由液面相对波高分布图。由图可知其在60 s后开始进入平稳状态，其波高历时曲线与激励曲线运动规律一致，呈简谐波动规律。通过比较各个频率工况的稳定波高幅值，可知在外部激励频率在达到固有频率时，会发生最为强烈的液体晃荡。

如图12所示，b=0.003 m振幅工况下，在开始的30 s内，呈现了明显的非线性现象，随后压力幅值趋于稳定。当激励频率变化为与固有频率值相差较大时，液舱晃荡对舱壁上压力的稳定波峰波谷差值减小，压力-时间历程曲线变窄。

3.3 网格无关性验证

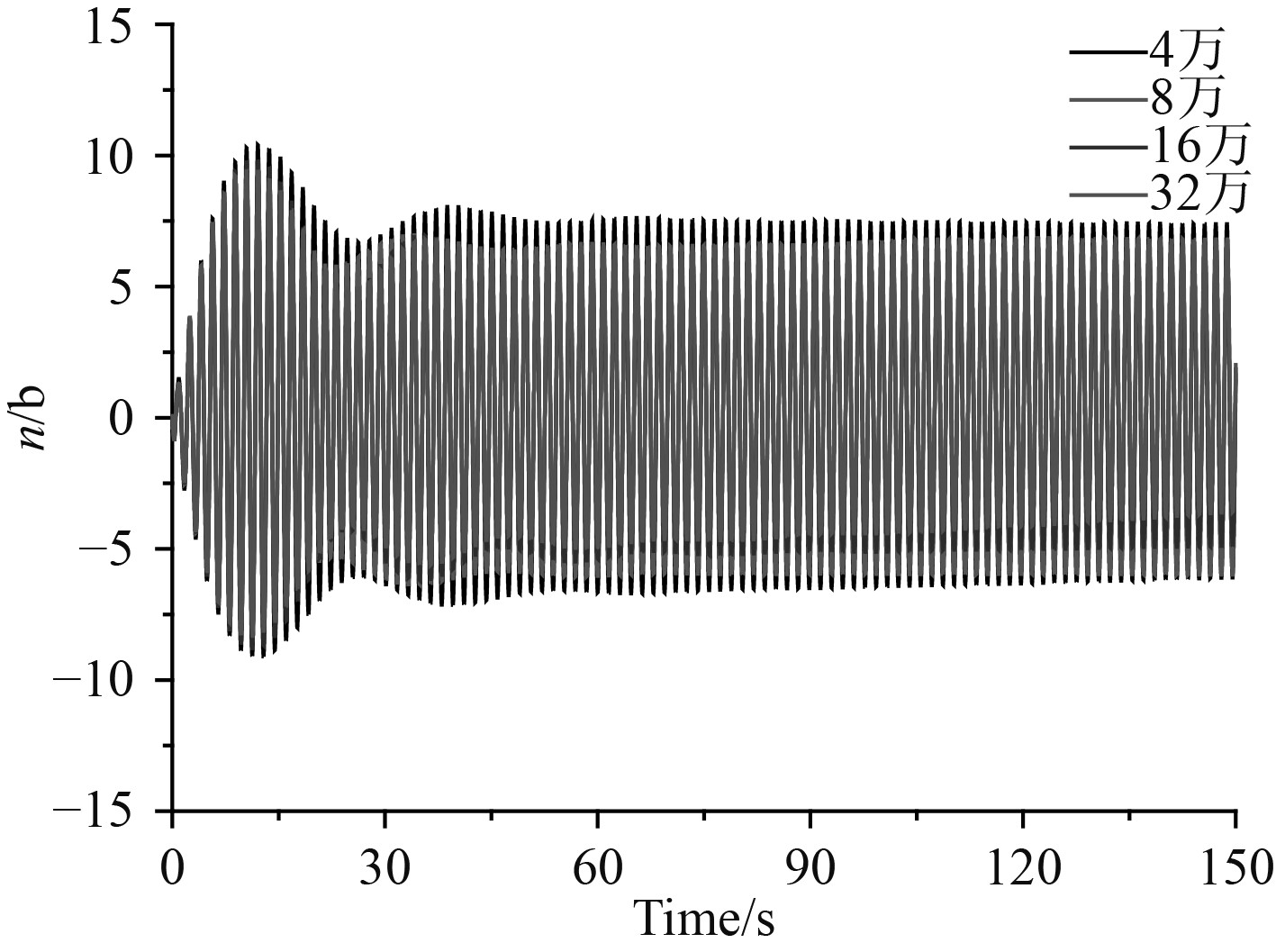
通过对半圆-矩形液舱的网格进行加密和加疏处理，对已划分网格的无关性进行验证，方法为整体加密加疏，网格无关性采用网格数量分别为4万、8万、16万和32万，其中 ${\omega _0}$ =4 rad/s，b=0.003 m，图13和图14为不同网格示意图及自由液面相对波高曲线（ $ \eta /b $ ）。

由图14可以看出，4万、8万、16万和32万网格数量下， $ \eta /b $ 分别稳定在7.4，6.58，6.55和6.65，其中网格数为4万工况的相对波高分布情况与其他工况差异较大，说明在网格数增加到8万以上时，计算结果不受网格数量的影响，其精度符合网格无关性要求。

4 结　论

数值模拟计算得到的结论如下：

1）对于本文研究的二维水平液舱的晃荡问题，计算2种特殊工况下自由液面晃荡状态，并将数值模拟计算和解析解结果相比较，2条曲线的误差较小，证明了本文计算选取的液舱模型的可靠性。

2）矩形和半圆-矩形液舱模型下， $\omega = {\omega _0}$ 时，波峰的最小值随着激励振幅增大而增大，最大值减小，曲线总体呈现向上偏离的趋势； $\omega $ =0.5 ${\omega _0}$ 时，随着数值模拟计算的推进，曲线的最大相对波高值在下降一段时间后收敛。2种形状液舱模型均呈现了一段时间的非线性现象，随后幅值趋于稳定。不同振幅的曲线差别较小，这证明该情况下施加的激励晃荡是与线性相接近的。

3）通过对比矩形液舱模型和半圆-矩形液舱模型不同振幅工况下的自由液面波动规律，半圆-矩形液舱模型波高波峰波谷差值略大，波动周期略长。总体而言，2种液舱模型晃荡时自由液面波高总体变化规律较为接近，吻合度较高。

4）半圆-矩形液舱模型下，在位移振幅工况选取0.003 m和0.004 m的情况下，舱内液体晃荡的冲击会对舱壁施加压力，且此压力有周期性规律；在开始的40 s内，均呈现了较为显著的非线性现象，随后压力幅值趋于一个稳定值。且随着激励振幅的增大，舱壁监测点受到的压力波峰值减小而波谷值增大，波峰波谷的差值逐渐稳定。在0.003振幅工况下，随着激励频率的增大，液舱晃荡对舱壁上监测点压力的稳定范围减小。

5）半圆-矩形液舱模型下，在不同的激励频率工况下，在固有频率附近自由液面波高值达到最大值；激励频率小于或大于固有频率时， $ \eta /b $ 值随着 $\omega $ 远离固有频率值而减小。在60 s后波高曲线趋于收敛，其波高历时曲线与激励曲线运动规律一致，呈简谐波动规律。在给定的频率工况达到水舱中流体的固有频率工况时，就会激发出最为强烈的液体晃荡，其晃荡幅值远远超过其他频率工况。因此在海洋工程研究过程中，应尽可能地控制好外部施加的频率使其远离固有频率，才能保障航行器航行时的安全。

5 结　语

本文通过数值计算与解析解的对比验证了二维模型模拟晃荡问题的精确性，计算了2种形状液舱模型在不同激励振幅、频率工况下波高分布，分析了舱壁监测点压力关于时间历程曲线的规律。在外界激励频率接近固有频率工况时，液舱将产生最为强烈的晃荡，其晃荡幅度远大于其他频率工况，该特殊工况是海洋科研界探究晃荡对航行器整体运动影响最为关注的问题，具有十分重要的工程应用价值。