超空泡航行体是指利用空泡减阻技术,使航行体水下阻力达到与空气阻力相同的量级,致使其航速获得极大提升。超空泡航行体相关技术的成功应用是超空泡鱼雷,1977年苏联成功研制出第一代超空泡鱼雷−“暴风雪”鱼雷,之后,世界各国以“暴风雪”鱼雷为背景的研究逐步开展,包括超空泡技术、航行体结构设计和航行稳定控制等领域,同时对超空泡航行体搭载自导系统也成为研究热点。超空泡航行体搭载自导系统的难点在于:1)由于光信号在水中衰减较快,所以水中通信主要以声信号为主,但是超空泡航行体在航行中巨大的自噪声会大大降低信噪比。2)声呐基阵需要集成在空化器锥内及周围,结构设计难度大。同时对于超空泡航行体,其物理特性致使其机动能力较弱,在导引时需要更长的声呐采集距离以避免过高的角速度。
本文首先论述超空泡航行体基于主动倾斜转弯控制策略的最大机动能力,并以此为前提计算了多种态势条件下,基于比例导引的需用最短自导作用距离,提出了弱机动条件下,自导超空泡航行体无法满足多数态势的导引要求,所以类似超空泡鱼雷这样带有攻击性质的超空泡航行体,目前仍应以直航攻击为主。
1 超空泡航行体最大机动能力探究 1.1 动力学模型根据文献[1]可知,传统的采用尾垂直舵实现航行体航向偏转的方式并不适用于超空泡航行体,倾斜转弯控制策略是超空泡航行体可行的机动方式之一。针对超空泡航行体自导作用距离计算需求,对超空泡航行体基于主动倾斜转弯控制策略的机动能力进行评估,参考文献[2]给出超空泡航行体动力学模型:
| $ \left\{ \begin{gathered} \dot v = {a_{11}}{B_1} ,\hfill \\ \dot \alpha = {{[( - {a_{11}}\alpha + {a_{12}}){B_1} + {a_{13}}{B_2} + {a_{14}}{B_6}]} \mathord{\left/ {\vphantom {{[( - {a_{11}}\alpha + {a_{12}}){B_1} + {a_{13}}{B_2} + {a_{14}}{B_6}]} v}} \right. } v},\hfill \\ \dot \beta = {{[( - {a_{11}}\beta - {a_{15}}){B_1} - {a_{13}}{B_3} + {a_{14}}{B_5}]} \mathord{\left/ {\vphantom {{[( - {a_{11}}\beta - {a_{15}}){B_1} - {a_{13}}{B_3} + {a_{14}}{B_5}]} v}} \right. } v},\hfill \\ {\omega _x} = {{({B_4} - {a_{19}}{B_2} + {a_{20}}{B_3} - {a_{21}}{B_5} - {a_{22}}{B_6})} \mathord{\left/ {\vphantom {{({B_4} - {a_{19}}{B_2} + {a_{20}}{B_3} - {a_{21}}{B_5} - {a_{22}}{B_6})} {{a_{23}}}}} \right. } {{a_{23}}}},\hfill \\ {\omega _y} = {a_{16}}{B_1} + {a_{14}}{B_3} - {a_{17}}{B_5},\hfill \\ {\omega _z} = - {a_{18}}{B_1} - {a_{14}}{B_2} + {a_{17}}{B_6}。\hfill \\ \end{gathered} \right. $ | (1) |
式中:
| $ \begin{gathered} {B_1} = {f_1}(v,\alpha ,\beta ,{\delta _e},{\delta _r},{\delta _n},\theta ,{\omega _x},{\omega _y},{\omega _z},T),\hfill \\ {B_2} = {f_2}(v,\alpha ,\beta ,{\delta _e},{\delta _n},\theta ,\psi ,\varphi ,{\omega _x},{\omega _y},{\omega _z}) ,\hfill \\ {B_3} = {f_3}(v,\alpha ,\beta ,{\delta _r},\theta ,\psi ,\varphi ,{\omega _x},{\omega _y},{\omega _z}) ,\hfill \\ {B_4} = {f_4}(v,\alpha ,\beta ,{\delta _b},\theta ,\psi ,\varphi ,{\omega _x},{\omega _y},{\omega _z},{M_{ox}}) ,\hfill \\ {B_5} = {f_5}(v,\alpha ,\beta ,{\delta _b},\theta ,\psi ,\varphi ,{\omega _x},{\omega _y},{\omega _z}),\hfill \\ {B_6} = {f_6}(v,\alpha ,\beta ,{\delta _e},{\delta _n},\theta ,\psi ,\varphi ,{\omega _x},{\omega _y},{\omega _z})。\hfill \\ \end{gathered} $ | (2) |
式中:
基于以上模型,开展超空泡航行体基于主动倾斜转弯控制策略的机动能力评估,超空泡航行体典型的机动弹道仿真曲线如图1所示。

|
图 1 典型机动弹道曲线 Fig. 1 Trajectory curve of typical maneuver |
根据倾斜转弯控制策略的力学分析可知,超空泡航行体横滚角越大,则首舵提供的水平分量越大,其机动能力便越强。不同横滚角对应的稳态旋回角速度及最大深度见表1。
|
|
表 1 不同横滚角对应的旋回角速度及最大深度 Tab.1 The angular velocity and maximum depth corresponding to different roll angle |
主动倾斜转向的机动控制策略下横滚角越大,机动能力越强,但大横滚角同时会带来垂直方向升力不足,导致航行体深度偏大问题。对于超空泡航行体来说,为了保证巡航段空泡形态的稳定,深度波动范围应不大于2 m。基于以上仿真结果可知,在45°横滚角下,航行体最大机动能力为6.5°/s,最大深度为6.75 m,在5±2 m的空泡稳定范围内;当横滚角增大至50°时,航行体最大深度为9.99 m,明显超出了空泡稳定的深度波动范围。
因此,在保证超空泡航行体空泡稳定的情况下,采用倾斜转弯控制策略的超空泡航行体的最大机动能力为6.5°/s,考虑到系统可靠性,将最大回转角速度设置为6°/s。在此基础上,研究超空泡航行体需要的最短自导作用距离。
2 需用最短自导作用距离探究 2.1 导引方式经典的导引方式有尾追法、固定提前角法、平行接近法和比例导引法,尾追法和固定提前角法对航行体和目标的速度比要求较高。当速度比大于2,采用尾追法接近目标时,航行体的角速度趋近无穷值,固定提前角法要求速度比满足
| $ 1 < p < \frac{2}{\sqrt{1+3{\mathrm{sin}}^{2}\eta }}。$ | (3) |
当目标是质点,速度比不满足上式时,航行体不可能命中目标。超空泡航行体速度高达200 kn,即使目标以30 kn全速前进,速度比也接近7,所以尾追法和固定提前角法不适用于超空泡航行体。
理论上,平行接近法要求的法向过载小于目标机动过程中的法向过载,但超空泡航行体的最大回转角速度为6°/s,机动能力普遍弱于要跟踪的目标,所以在某些态势条件下无法满足导引需用法向过载。
比例导引法是上述方法的一般形式,针对不同战场态势相选择应的比例导引系数,可以最大程度上削弱导引方式对航行体机动能力的影响。航行体与目标的相对运动关系如图2所示。

|
图 2 航行体与目标相对运动图 Fig. 2 The relative motion between vehicle and target |
图中,X为参考方向,TM为视线,r为相对距离,q为视线角,
根据图2建立相对距离和视线角的微分方程组如下:
| $ \left\{\begin{array}{l}\dot{r}={v}_{M}\mathrm{cos}{\eta }_{M}-{v}_{T}\mathrm{sin}{\eta }_{T},\\ \dot{q}=\dfrac{{v}_{T}\mathrm{sin}{\eta }_{T}-{v}_{M}\mathrm{sin}{\eta }_{M}}{r},\\ {\eta }_{T}=q-{C}_{T},\\ {\eta }_{M}=q-{C}_{M}。\end{array}\right. $ | (4) |
导引律为
| $ \dot{{C}_{T}}=a\cdot \dot{q},$ | (5) |
其中a为比例导引系数。
对式(4)中二式两端求导,可以得到
| $ \ddot{q}=-\frac{2\dot{r}+a{v}_{T}\mathrm{cos}{\eta }_{T}}{r}\dot{q}+\frac{{v}_{M}\omega }{r}\mathrm{cos}{\eta }_{M}。$ | (6) |
其中
| $ \ddot{q}=-{k}_{1}\dot{q}+{k}_{2} 。$ | (7) |
若要使
| $ a > \dfrac{2\left|\dfrac{{\rm{d}}r}{{\rm{d}}t}\right|}{v\cdot \mathrm{cos}{\eta }_{T}} 。$ | (8) |
当比例导引系数满足上述条件时,航行体导引过程中的角速度会逐渐收敛。但a不宜太大,否则视线角变化率
| $ a=\dfrac{2\left|\dfrac{{\rm{d}}r}{{\rm{d}}t}\right|}{v\cdot \mathrm{cos}{\eta }_{T}}+1。$ | (9) |
参考声自导鱼雷的攻击过程,超空泡航行体导引的一般流程为:结合战场初始态势,航行体先以某一航向直航,在航行一段距离后自导系统开机并捕获目标,转入导引段直至跟踪到目标。
航行体初始航行段的航向有2种确定方式:现在位、提前角。现在位指航行体朝目标当前方位航行。提前角指航行器根据目标当前方位和速度比,计算出直航的期望相遇点,并向该点航行。
若目标当前相对航行体的方位角为
| $ {C}_{T0}={q}_{0},$ | (10) |
采用提前角方式的航向为:
| $ {C}_{T0}={q}_{0}+\mathrm{asin}\frac{\mathrm{sin}\left[{q}_{0}-{C}_{M}-sign({q}_{0}-{C}_{M})\right]}{p} 。$ | (11) |
目标在发现己方或被跟踪时,除采用声诱饵和深弹拦截外,通常会以机动方式躲避跟踪,具体表现为目标经过时间
与航行体航向成相同角度的方向有4个,目标应采用“小舷角相向转向”、“大舷角背离转向”的原则,且选择需要旋转角度最小的方向,以实现快速逃离。定义角
| $ \left\{\begin{array}{l} {C}_{M}={C}_{T0}-\theta,-\text{π} \leqslant \alpha \leqslant -\dfrac{\text{π} }{2},\\ {C}_{M}={C}_{T0}-\text{π} +\theta ,-\dfrac{\text{π} }{2} < \alpha < 0,\\ {C}_{M}={C}_{T0}-\text{π} -\theta ,0\leqslant \alpha < \dfrac{\text{π} }{2},\\ {C}_{M}={C}_{T0}+\theta ,\dfrac{\text{π} }{2}\leqslant \alpha < \text{π}。\end{array}\right. $ | (12) |
单次仿真试验流程为:目标低速直航,航行体在特定方位和距离,采用现在位或提前角方式进行直航,航行时间由平台预先设定。假设航行体在自导开机时就可捕获目标,并根据当前目标与己方的位置关系,选择合适的比例导引系数,进入导引段跟踪接近目标。目标在航行体直航段时就发出预警,经过一定反应时间,立即高速转入逃离航向。
假设航行体在导引过程中没有最大角速度限制,各种态势均能命中目标。改变初始方位、距离以及直航时间,进行多次仿真实验,统计出导引过程中航行体最大角速度不超过6°/s的临界态势,计算出这些态势对应的自导开机时航行体到目标的距离,距离的最大值是超空泡航行体导引需要的最短作用距离。
仿真实验对象是超空泡航行体和某型巡洋舰,基本参数设置见表2。
|
|
表 2 参数设定 Tab.2 Parameter setting |
设置初始距离为7000 m,目标探测时间为10 s,逃离角度为90°。图3和图4中曲面为各初始态势下,航行体导引过程的最大角速度,平面为6°/s的角速度限制。

|
图 3 提前角方式 Fig. 3 Ahead position method |

|
图 4 现在位方式 Fig. 4 Current position method |
“提前角”方式要求的最短自导作用距离为1771.6 m,对应态势为初始方向舷角30°,航行体直航时间54 s。
“现在位”方式要求的最短自导作用距离为1987.6 m,对应态势为初始方向舷角77°,航行体直航时间50 s。
“提前角”方式要求的自导作用距离比“现在位”的更短,这是因为前者发射方式对目标落点进行了预判,一定程度上减小了航行体在导引过程中需要旋回的角度。
3.2 逃离角度对需用自导距离的影响参考水面舰艇采用纯机动规避声自导鱼雷的基本原则,即在有来袭鱼雷预警后尽快驶离鱼雷自导搜索带,而其中最有效的策略是沿垂直于鱼雷航向的方向进行逃离,即逃离角度
设置目标机动反应时间为10 s,初始距离为5000 m,逃离角度为0∶1∶90°。
由图5可知,当目标逃离航向与航行体直航航向夹角在40°以内时,对需用自导距离无影响。但随着逃离角度的逐渐增大,需用自导距离大体呈增加的趋势,并在90°达到最大值,目标垂直逃离意味着航行体需要转过更大的角度来进行导引跟踪,所以对自导探测距离要求更高。

|
图 5 需用自导距离随逃离角度变化图 Fig. 5 Plot of necessary homing distance with escape angle |
设置目标机动反应时间为10 s,目标逃离角度90°,初始距离为3000∶1000∶7000 m。
由图6可知,导引需要的最短自导作用距离随初始距离增加而增大,7 000 m时“提前角”攻击方式的自导距离为1 771.61 m,而“现在位”的是1 987.61 m。更长的初始距离意味着目标有更加充分的时间转入逃离航行并高速驶离,所以要求航行体在更远的位置就能发现目标并进行跟踪。

|
图 6 需用自导距离随初始距离变化图 Fig. 6 Plot of necessary homing distance with initial distance |
不同水面舰艇的机动反应时间
设置初始距离为5 000 m,目标探测时间为5∶5∶20 s。
由图7可知,需用自导作用距离随目标机动反应时间增加而减少,5 s时“提前角”攻击对应的需用自导距离为1 533.62 m,“现在位”对应1 722.92 m。目标越早对来袭航行体作出反应,越能快速转入到逃离航向,并且由于逃离航向与航行体航向垂直,所以需要航行体在较远距离就开始导引机动,以避免导引过程中过大的机动能力需求。

|
图 7 需用自导距离随目标机动反应时间变化图 Fig. 7 Plot of necessary homing distance with target response time to maneuver |
遍历各个变量,即初始距离3 000∶1 000∶7 000 m,目标逃离角度0∶10∶90°,目标机动反应时间5∶1∶20 s,结果如图8和图9所示。
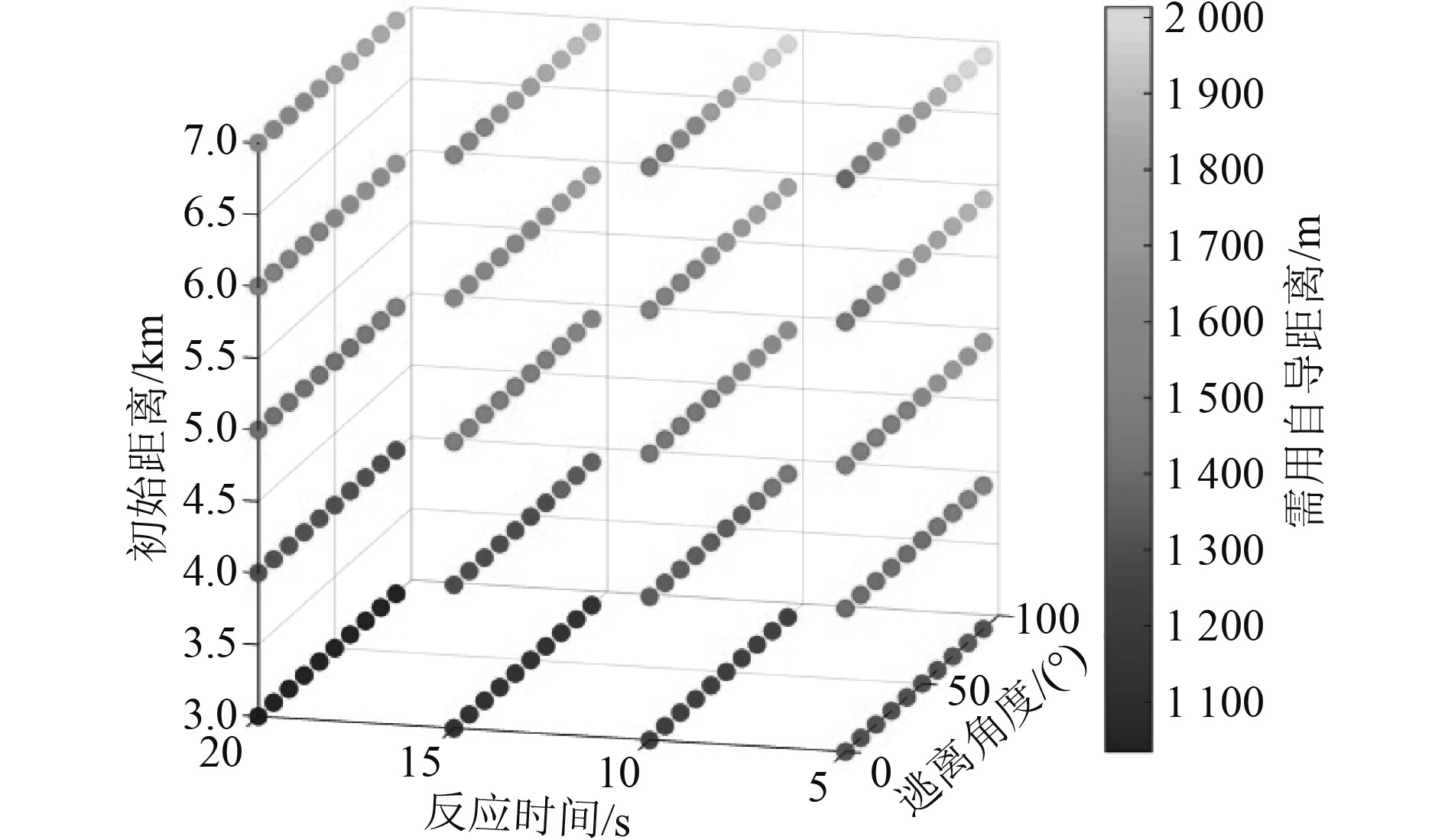
|
图 8 “现在位”攻击的多态势需用自导距离 Fig. 8 Necessary homing distance in various situations through current position method |

|
图 9 “提前角”攻击的多态势需用自导距离 Fig. 9 Necessary homing distance in various situations through ahead position method |
可知,在远距离追踪机动反应迅速且以大角度逃离的目标,对自导距离要求高,其中初始距离的影响更为显著。采用“提前角”方式能够有效降低同一态势下的机动能力需求。
4 结 语在建立超空泡航行体动力学模型的基础上,仿真分析出在保证空泡形态稳定下,超空泡航行体基于主动倾斜转弯控制策略的最大机动角速度约为6°/s,并以此为前提探究其需用最短自导作用距离。仿真实验分析了航行体初始段航向、目标逃离角度、初始距离和目标机动反应时间对航行体需要的最短自导作用距离的影响。结果表明在不考虑自导扇面、波束周期、探测误差以及目标声对抗的理想情况下,超空泡航行体需要的最短自导作用距离均在1 km以上,部分态势接近2 km。
在实际战场的复杂环境中,需要的自导作用距离会更长,并且由于超空泡航行体航行噪声大,头部又安装有空泡发生器,以目前的技术手段无法满足其需求。所以以超空泡鱼雷为代表的一系列超空泡航行体武器,仍应采取直航攻击的方式。
| [1] |
罗凯, 李代金, 黄闯. 超空泡航行技术的理论基础[M]. 北京: 科学出版社, 2016.
|
| [2] |
张宇文, 袁绪龙, 邓飞. 超空泡航行体流体动力学[M]. 北京: 国防工业出版社, 2014.
|
| [3] |
陈颜辉. 水面舰艇综合防御鱼雷行动与技术发展[C]//中国兵工学会、重庆市科学技术协会. OSEC首届兵器工程大会论文集中国兵工学会、重庆市科学技术协会: 兵器装备工程学报编辑部, 2017: 3.
|
| [4] |
蒋运华, 安伟光, 安海. 超空泡运动体水平面运动弹道特性研究[J]. 弹箭与制导学报, 2012, 32(6): 117-120+124. DOI:10.3969/j.issn.1673-9728.2012.06.035 |
| [5] |
李代金, 罗凯, 党建军, 等. 超空泡水下航行体空间运动建模与弹道仿真[J]. 兵工学报, 2012, 33(8): 956-961. |
| [6] |
罗凯, 党建军, 王育才, 等. 超高速水下航行体纵平面运动特性分析[J]. 鱼雷技术, 2007(5): 37-40. |
| [7] |
白涛, 蒋运华, 韩云涛. 基于水洞实验的超空泡形态的动态估计研究[J]. 工程力学, 2017, 34(11): 249-256. DOI:10.6052/j.issn.1000-4750.2016.07.0563 |
| [8] |
王威, 王聪, 宋武超, 等. 侧滑角对超空泡航行体转弯运动沾湿区域的影响[J]. 振动与冲击, 2020, 39(12): 135-141. |
| [9] |
曹立飞, 曹红松, 刘鹏飞, 等. 固定鸭舵二维修正弹比例导引律参数优化[J]. 航空学报, 2021, 42(6): 604-614. |
| [10] |
宋书龙, 吕瑞, 周景军, 等. 基于主动倾斜转弯的超空泡航行体机动控制方法[J]. 水下无人系统学报, 2019, 27(6): 607-613. |
| [11] |
李洋, 刘明雍, 张小件. 基于自适应RBF神经网络的超空泡航行体反演控制[J]. 自动化学报, 2020, 46(4): 734-743. |
| [12] |
陈颜辉. 水面舰艇综合防御鱼雷决策关键技术[J]. 火力与指挥控制, 2019, 44(6): 102-105. DOI:10.3969/j.issn.1002-0640.2019.06.020 |
| [13] |
邓新文, 朱文振, 谢勇. 潜艇转向旋回防御主动声自导鱼雷的战术意义与作战运用[J]. 水下无人系统学报, 2019, 27(1): 65-70. |
| [14] |
王光辉, 宋艳波, 谢宇鹏, 等. 基于突防概率的寻的雷达最优自导距离模型[J]. 弹箭与制导学报, 2010, 30(4): 207-210. DOI:10.3969/j.issn.1673-9728.2010.04.059 |
| [15] |
陈颜辉, 黄文斌, 孙振新. 最优规避鱼雷策略与最小可规避预警距离[J]. 海军工程大学学报, 2014, 26(2): 76-79+84. |
 2022, Vol. 44
2022, Vol. 44
