0 引　言

近年来，无人船在油气勘探、水上搜救、近岸监控和海洋监测等方面应用越来越广泛^[1]。作为无人船发展的重要课题，欠驱动船舶的航迹跟踪控制受到了学者的关注。由于船舶在航行时受复杂海况的影响，航迹追踪的精确控制变得尤为困难，因此设计一种抗复杂海况干扰的高精度航迹追踪控制器。目前常见的航迹跟踪控制器有PID控制^[2]、滑模变结构控制^[3]、动态面控制^[4]、Lyapunov直接控制^[5]、模糊控制^[6]和神经网络控制^[7]等。目前船上装备的航向自动舵大部分为PID控制器，PID控制结构简单，计算量小，整定参数少并且有一套成型的整定规则，被广泛应用于船舶航迹跟踪控制，但PID控制并不能很好地应用于复杂多变的环境，当船舶航行在复杂海况的海域中，PID控制器不能达到预期的航迹跟踪精度要求，甚至可能使航迹追踪任务失败。

滑模变结构控制结构简单，控制精度高，对系统内部摄动与外部干扰的鲁棒性强，可用于复杂海况下的船舶航迹控制中。Fang等^[8]针对随机海浪下的船舶减摇和航迹跟踪问题，分别设计不同的滑模控制器进行航迹与减摇控制，仿真结果表明设计的滑模控制器能够达到很好的跟踪与减摇效果。廖煜雷等^[9]考虑到船舶控制模型的内部参数摄动与外界扰动的不确定性，利用动态滑模与反演控制设计一种自适应路径跟踪控制器，仿真表明该控制器能达到很好的效果。

本文根据Super-twisting 2阶滑模与自抗扰控制理论，设计一种基于Super-twisting的2阶滑模自抗扰控制算法。该算法利用扩张状态观测器估计并补偿复杂海况下的外界风浪干扰，并使用Super-twisting 2阶滑模实现航迹的高精度控制，消除控制输出抖振，仿真实验证明了该方法的优越性。

1 模型描述

船舶的MMG分离模型^[10]描述如下：

$ \left\{ \begin{aligned} &\dot x = u\cos \psi - v\sin \psi，\\ &\dot y = u\sin \psi + v\cos \psi，\\ &\dot \psi = r ，\\ &\dot u = \frac{{\left( {m + {m_y}} \right)vr + {X_H} + {X_P} + {X_R} + {X_{{\rm{disturb}}}}}}{{m + {m_x}}} ，\\ &\dot v = \frac{{\left( {m + {m_x}} \right)ur + {Y_H} + {Y_P} + {Y_R} + {Y_{{\rm{disturb}}}}}}{{m + {m_y}}} ，\\ &\dot r = \frac{{{N_H} + {N_P} + {N_R} + {N_{{\rm{disturb}}}}}}{{{I_{zz}} + {J_{zz}}}} 。\\ \end{aligned} \right. $

(1)

式中： $ x,y,\psi $ 分别为船舶在大地坐标系下的纵向位置、横向位置以及首向角； $ u,v,r $ 分别为船体坐标系下船舶的纵向速度、横向速度和转首角速度； $ m $ 为船舶的质量， $ {m_x} $ 与 $ {m_y} $ 为船舶在纵向与横向的附加质量； $ {I_{zz}} $为船舶的 转首惯性矩， $ {J_{zz}} $ 为附加惯性矩； ${X}_{H},{Y}_{H} , $ $ {N}_{H}$ 为裸船力和力矩； $ {X}_{P},{Y}_{P},{N}_{P} $ 为螺旋桨力和力矩， $ {X}_{R},{Y}_{R},{N}_{R} $ 为舵力和力矩； ${X}_{{\rm{disturb}}},{Y}_{{\rm{disturb}}},{N}_{{\rm{disturb}}}$ 为干扰力和力矩。

由于船舶MMG模型结构复杂，水动力参数很多，不能用于控制器的设计。通常在自动舵设计中，采用Nomoto方程进行控制器的设计，2阶非线性Nomoto模型^[11]的表达式如下：

$ \ddot \psi + \frac{K}{T}\left( {\alpha \dot \psi + \beta {{\dot \psi }^3}} \right) = \frac{K}{T}\delta + d 。$

(2)

式中： $ K $ 为Nomoto模型的增益参数； $ T $ 为时间常数； $ \alpha ,\beta $ 均为Nomoto模型的非线性参数，这4个参数均与航速有关； $ d $ 为外部风浪干扰。

控制目标为根据2阶非线性Nomoto模型设计首向控制器结合视线导航算法完成船舶的航迹控制。

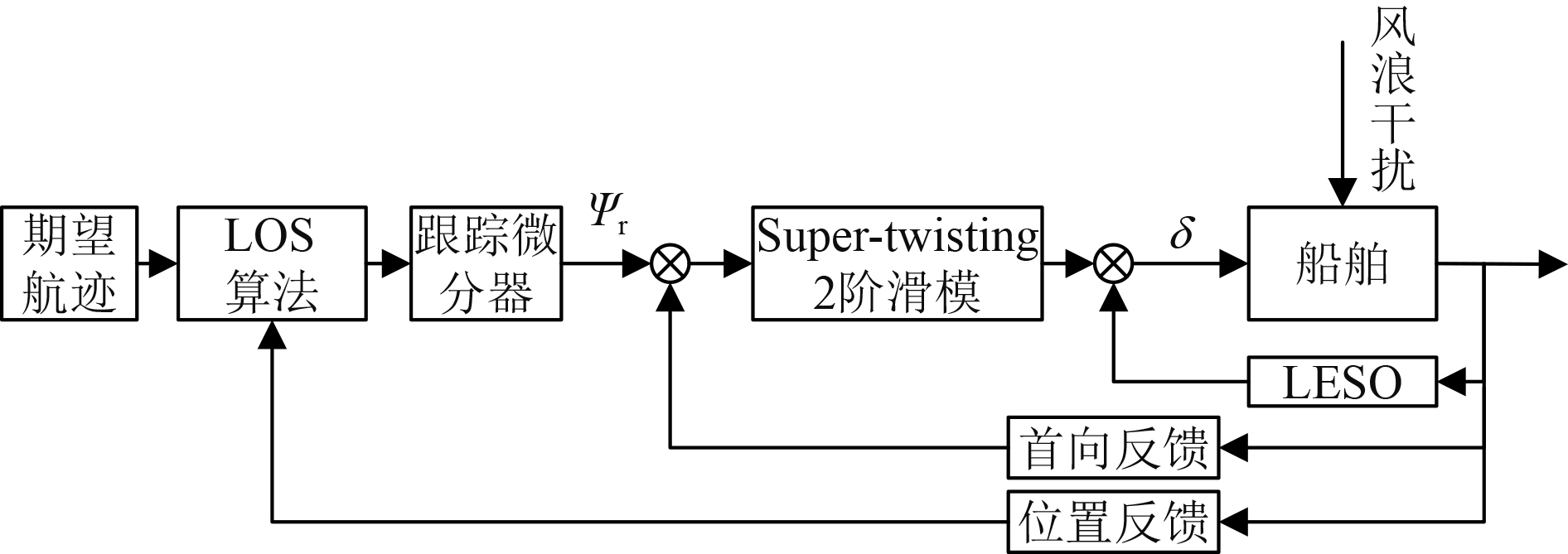
2 控制器设计

控制器设计分为：1）设计跟踪微分器^[12]，得到平滑的期望首向信息以及其微分信息；2）设计线性扩张状态观测器^[13]（LESO），估计船舶的首向角速度和未建模动态及外部干扰，并对其进行补偿；3）设计Super-twisting2阶滑模控制器^[14]，提高系统的控制性能。控制器的结构形式如图1所示。

2.1 跟踪微分器设计

跟踪微分器是自抗扰控制的组成部分之一，能够平滑过渡过程的信号，并提取微分信号，从而防止控制初始阶段和期望输入切换阶段对系统的冲击。非线性跟踪微分器的一般形式为：

$ \left\{ \begin{aligned} &{{\dot v}_1} = {v_2} ，\\ &{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \\ &{{\dot v}_{n - 1}} = {v_n}，\\ &{{\dot v}_n} = {r^n}f\left( {{v_1} - v,\frac{{{v_2}}}{r}, \cdots ,\frac{{{v_n}}}{{{r^{n - 1}}}}} \right) 。\end{aligned} \right. $

(3)

式中： $ v $ 为微分器的输入信号， $ {v_i}(i = 1,2, \cdots ,n) $ 为输出信号； $ r $ 为速度因子， $ r $ 越大跟踪速度越快。

在船舶航迹控制中，航迹点的切换会造成期望首向突变，且传统的LOS算法不能输出期望首向的导数与2阶导数，这给控制器的设计带来很大困难。因此设计3阶线性跟踪微分器平滑期望首向的突变，并实时输出期望首向的1阶导数与2阶导数信息。3阶线性跟踪微分器的形式如下：

$ \left\{ \begin{aligned} &{{\dot v}_1} = {v_2} ，\\ & {{\dot v}_2} = {v_3} ，\\ &{{\dot v}_3} = - {r^3}\left( {{v_1} - {\psi _d}} \right) - 3{r^2}{v_2} - 3r{v_3} 。\end{aligned} \right. $

(4)

式中： $ {\psi _d} $ 为船舶的期望首向角； $ {v_1},{v_2},{v_3} $ 分别为跟踪微分器输出的船舶期望首向角、首向角速度以及角加速度。

由式(4)可以得到 $ {v_1} $ 与 $ {\psi _d} $ 的传递函数为：

$ G\left( s \right) = \frac{{{r^3}}}{{{s^3} + 3r{s^2} + 3{r^2}s + {r^3}}}。$

(5)

可以看出：当速度因子 $ r > 0 $ 时，特征多项式 ${s^3} + $ $ 3r{s^2} + 3{r^2}s + {r^3} = {(s + r)^3}$ 满足Hurwitz条件，则跟踪微分器稳定。

2.2 线性扩张观测器设计

将船舶的2阶非线性Nomoto方程式(2)改写成：

$ \left\{ \begin{aligned} &\dot \psi = r ，\\ &\dot r = f\left( {\dot \psi ,d} \right) + {b_0}\delta 。\end{aligned} \right. $

(6)

式中： $f\left( {\dot \psi ,d} \right){\text{ = }} - {{K\left( {\alpha \dot \psi + \beta {{\dot \psi }^3}} \right)} \mathord{/ {\vphantom {{K\left( {\alpha \dot \psi + \beta {{\dot \psi }^3}} \right)} T}} } T} + d$ 为船舶内部模型信息与外部误差组成的总干扰， $ {b_0} = {K \mathord{\left/ {\vphantom {K T}} \right. } T} $ 为控制增益。

使系统状态量 $ {x}_{1}=\psi ，{x}_{2}=r，{x}_{3}=f $ ，其中 $ {x_3} $ 为被扩张的状态量，组成扩张状态空间为：

$ \left\{ \begin{aligned} &{{\dot x}_1} = {x_2} ，\\ &{{\dot x}_2} = {x_3} + {b_0}\delta ，\\ & {{\dot x}_3} = h。\end{aligned} \right. $

(7)

式中， $ h $ 为总干扰量 $ f $ 的导数，假设 $ h $ 有界， $ \left| h \right| \leqslant \rho $ ， $ \rho $ 为一个正常数。

根据扩张状态空间(7)，设计线性扩张状态观测器为：

$ \left\{ \begin{aligned} & {{\dot {\hat x}}_1} = {{\hat x}_2} + {l_1}\left( {{x_1} - {{\hat x}_1}} \right)，\\ &{{\dot {\hat x}}_2} = {{\hat x}_3} + {l_2}\left( {{x_1} - {{\hat x}_1}} \right) + {b_0}\delta ，\\ &{{\dot {\hat x}}_3} = {l_3}\left( {{x_1} - {{\hat x}_1}} \right) 。\end{aligned} \right. $

(8)

式中： $ {l_1},{l_2},{l_3} $ 为观测器增益，其选取应使特征方程 $ {s^3} + {l_1}{s^2} + {l_2}s + {l_3} $ 满足Hurwitz条件；为了方便ESO整定，本文使用带宽方法将观测器的极点均配置在 $ - {\omega _o} $ 处， $ {\omega _o} > 0 $ 为ESO的带宽，则观测器的3个增益参数分别为 $ {l_1} = 3{\omega _o},{l_2} = 3\omega _o^2,{l_3} = \omega _o^3 $ 。

2.3 Super-twisting 2阶滑模设计

以上述状态空间(7)设计滑模控制器，首先定义系统的跟踪误差为：

$ {e}_{\psi }={x}_{1}-{\psi }_{d}\text{，}{\dot{e}}_{\psi }={\widehat{x}}_{2}-{\dot{\psi }}_{d}，$

(9)

设计线性滑模面为：

$ s = {\dot e_\psi } + c{e_\psi }，$

(10)

则滑模面导数为：

$ \begin{split} \dot s =& {{\ddot e}_\psi } + c{{\dot e}_\psi }= {{\dot {\hat x}}_2} - {{\ddot \psi }_d} + c{{\dot e}_\psi } =\\ &{{\hat x}_3} + {b_0}\delta - {{\ddot \psi }_d} + c{{\dot e}_\psi } 。\end{split} $

(11)

为了消除观测器误差对控制系统的影响，设计Super-twisting 2阶滑模趋近率如下：

$ \dot s = - {k_1}{\left| s \right|^{0.5}}{{\rm{sgn}}} \left( s \right) - {k_2}\int_0^t {{{\rm{sgn}}} \left( s \right){\rm{d}}\tau } 。$

(12)

结合式(7)与式(12)可得出舵的控制率为：

$ \begin{split} \delta = &\frac{1}{{{b_0}}}({{\ddot \psi }_d} - c{{\dot e}_\psi } - {{\hat x}_3} - {k_1}{\left| s \right|^{0.5}}{{\rm{sgn}}} \left( s \right) \hfill- \\ & {k_2}\int_0^t {{{\rm{sgn}}} \left( s \right){\rm{d}}\tau } ) 。\end{split} $

(13)

3 稳定性证明 3.1 扩张观测器稳定性证明

由式(7)和式(8)得到LESO的观测误差方程为：

$ \left\{ \begin{aligned} &{{\tilde x}_1}{\text{ = }}{x_1} - {{\hat x}_1} ，\\ &{{\tilde x}_2}{\text{ = }}{x_2} - {{\hat x}_2}，\\ &{{\tilde x}_3}{\text{ = }}{x_3} - {{\hat x}_3} ，\\ &{{\dot {\tilde x}}_1} = {{\tilde x}_2} - {l_1}{{\tilde x}_1} ，\\ &{{\dot {\tilde x}}_2} = {{\tilde x}_3} - {l_2}{{\tilde x}_1}，\\ &{{\dot {\tilde x}}_3} = h - {l_3}{{\tilde x}_1} 。\end{aligned} \right. $

(14)

定义 $ {X_1} = {\tilde x_1} $ ， $ {X_2} = {\tilde x_2} - {l_1}{\tilde x_1} $ ， ${X_3} = {\tilde x_3} - {l_2}{\tilde x_2} - {l_1}{\dot {\tilde x}_1}$ ，则可构成状态方程：

$ \left\{ \begin{aligned} &{{\dot X}_1} = {X_2} \\ &{{\dot X}_2} = {X_3} \\ &\begin{aligned}{{\dot X}_3} = &{{\dot {\tilde x}}_3} - {l_2}{{\dot {\tilde x}}_2} - {l_1}{{\ddot {\tilde x}}_1}= \\ &- {l_3}{{\tilde x}_1} + h - {l_2}\left( {{{\tilde x}_3} - {l_2}{{\tilde x}_2}} \right) -\\ &{l_1}\left[ {{{\tilde x}_3} - {l_2}{{\tilde x}_2} - {l_1}\left( {{{\tilde x}_2} - {l_1}{{\tilde x}_1}} \right)} \right] = \\ &- {l_1}{X_3} - {l_2}{X_2} - {l_3}{X_1} + h 。\end{aligned} \end{aligned} \right. $

(15)

可以看出，式(15)的特征方程为 $ {s^3} + {l_1}{s^2} + {l_2}s + {l_3}= $ $ $ {\left( {s + {\omega _o}} \right)^3} $ ，其全部特征根均为负值，满足Hurwitz条件，因此观测误差方程(14)渐进稳定；但由于干扰项 $ h $ 的存在，LESO存在观测误差，当观测时间趋于无穷时，观测系统达到稳态，即

$ {\dot{X}}_{1}=0\text{，}{\dot{X}}_{2}=0\text{，}{\dot{X}}_{3}=0 。$

(16)

由此可得出各个状态的稳态误差为：

$ \left\{ \begin{gathered} \mathop {\lim }\limits_{t \to \infty } \left| {{{\tilde x}_1}} \right| = \frac{\rho }{{{l_3}}} = \frac{\rho }{{\omega _o^3}} ，\\ \mathop {\lim }\limits_{t \to \infty } \left| {{{\tilde x}_2}} \right| = \frac{{{l_1}\rho }}{{{l_3}}} = \frac{{3\rho }}{{\omega _o^2}} ，\\ \mathop {\lim }\limits_{t \to \infty } \left| {{{\tilde x}_3}} \right| = \frac{{{l_2}\rho }}{{{l_3}}} = \frac{{3\rho }}{{\omega _o^{}}} 。\end{gathered} \right. $

(17)

至此，LESO稳定性得证，且从式(17)可以看出，带宽参数 $ {\omega _o} $ 越大，LESO的稳态误差越小，因此增大带宽参数可以提升观测器的估计性能，但过大的带宽会引入高频噪声，因此在参数整定时要综合考虑系统的跟踪性能和耐噪性。

3.2 有限时间收敛证明

将式(13)代入式(2)可得

$ \dot s = - {k_1}{\left| s \right|^{0.5}}{{\rm{sgn}}} \left( s \right) - {k_2}\int_0^t {{{\rm{sgn}}} \left( s \right){\rm{d}}\tau } + {\tilde x_3} 。$

(18)

将式(18)写成如下形式：

$ \left\{ \begin{aligned} &\dot s = - {k_1}{\left| s \right|^{0.5}}{{\rm{sgn}}} \left( s \right) + \sigma，\\ &\dot \sigma = - {k_2}{{\rm{sgn}}} \left( s \right) + {{\dot {\tilde x}}_3} 。\end{aligned} \right. $

(19)

假设扩张状态观测器的干扰观测误差导数 ${\dot {\tilde x}}_3$ 有界，既满足 $ \left| {{{\dot {\tilde x}_3}}} \right| \leqslant \upsilon $ ，其中 $ \upsilon $ 是一个正常数；干扰观测误差导数可以写成以下形式：

$ {\dot {\tilde x}}_3 = \upsilon \frac{{{{\left| s \right|}^{0.5}}{{\rm{sgn}}} \left( s \right)}}{{{{\left| s \right|}^{0.5}}}} 。$

(20)

式(20)可以转换为以下形式：

$ \dot{{\boldsymbol{g}}}={\left|{g}_{1}\right|}^{-1}{\boldsymbol{Ag}}\text{，}{\boldsymbol{A}}=\left[\begin{array}{cc}-0.5{k}_{1}& 0.5\\ \upsilon -{k}_{2}& 0\end{array}\right] 。$

(21)

设计二次型李雅普诺夫函数为：

$ V{\text{ = }}{{\boldsymbol{g}}^{\rm{T}}}{\boldsymbol{Pg}} 。$

(22)

式中 ${\boldsymbol{P}}$ 为一个对称的正定矩阵，定义为：

$ {\boldsymbol{P}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {4{k_2} + k_1^2}&{ - {k_1}} \\ { - {k_1}}&2 \end{array}} \right]。$

(23)

对李雅普诺夫函数求导得

$ \begin{split} \dot V =& {{\dot {\boldsymbol{g}}}^{\rm{T}}}{\boldsymbol{Pg}} + {{\boldsymbol{g}}^{\rm{T}}}{\boldsymbol{P}}\dot {\boldsymbol{g}} = {\left| {{g_1}} \right|^{ - 1}}{{\boldsymbol{g}}^{\rm{T}}}\left( {{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{P}} + {\boldsymbol{PA}}} \right){\boldsymbol{g}} =\\ & - {\left| {{g_1}} \right|^{ - 1}}{{\boldsymbol{g}}^{\rm{T}}}{\boldsymbol{Qg}} 。\\[-15pt] \end{split} $

(24)

式中： $\boldsymbol{Q} = \dfrac{1}{2}\left[ {\begin{array}{*{20}{c}} {k_1^3 + 2{k_1}{k_2} + 2{k_1}\upsilon }&{ - k_1^2 - 2\upsilon } \\ { - k_1^2 - 2\upsilon }&{{k_1}} \end{array}} \right]$ ，为对称矩阵。

当控制器参数 ${k}_{1}{\text{和}}{k}_{2}$ 满足下式关系时，矩阵 $ {\boldsymbol{Q}} $ 为正定矩阵。

$ {k}_{1} > 0\text{，}{k}_{2} > \upsilon +\frac{2{\upsilon }^{2}}{{k}_{1}^{2}} 。$

(25)

式(25)可以转化为：

$ \dot V \leqslant - {\left| {{g_1}} \right|^{ - 1}}{\lambda _{\min }}({\boldsymbol{Q}}){\left\| {\boldsymbol{g}} \right\|^2} 。$

(26)

式中： ${\lambda _{\min }}({\boldsymbol{Q}})$ 为矩阵 ${\boldsymbol{Q}}$ 的最小特征值。

根据正定矩阵 $ P $ 和式(23)可得

$ {\lambda _{\min }}({\boldsymbol{P}}){\left\| {\boldsymbol{g}} \right\|^2} \leqslant V \leqslant {\lambda _{\max }}({\boldsymbol{P}}){\left\| {\boldsymbol{g}} \right\|^2} ，$

(27)

则

$ \frac{{{V^{0.5}}}}{{\lambda _{\max }^{0.5}({\boldsymbol{P}})}} \leqslant \left\| {\boldsymbol{g}} \right\| \leqslant \frac{{{V^{0.5}}}}{{\lambda _{\min }^{0.5}({\boldsymbol{P}})}} 。$

(28)

由 ${{\boldsymbol{g}}^{\rm{T}}} = \left[ {{g_1},{g_2}} \right]$ 可知， $\left| {{g_1}} \right| \leqslant \left\| {\boldsymbol{g}} \right\|$ ，则式(27)可进一步表达为：

$ \begin{split} \dot V \leqslant - {\left| {{g_1}} \right|^{ - 1}}{\lambda _{\min }}({\boldsymbol{Q}}){\left\| {\boldsymbol{g}} \right\|^2}\leqslant - {\lambda _{\min }}({\boldsymbol{Q}})\left\| {\boldsymbol{g}} \right\| \leqslant - \frac{{{\lambda _{\min }}({\boldsymbol{Q}})}}{{\lambda _{\max }^{0.5}({\boldsymbol{P}})}}{V^{0.5}} 。\end{split} $

(29)

根据文献[15]中有效时间收敛性定理可得，变量 ${g}_{1}{\text{和}}{g}_{2}$ 可以在有限时间内收敛到0，即滑模变量 $ s $ 可以在有限时间内收敛到0，证毕。

4 仿真验证

以长为47.4 m的执法船“海巡0208”轮作为仿真对象进行控制器验证。为了验证本文算法的优越性，将本文算法与传统的PID控制器进行航迹追踪控制对比，其中PID参数根据Nomoto模型的KT参数整定。

在仿真中，设置船舶的车令保持在1000 r/min，稳定航速为6.4 m/s，根据辨识方法计算出参数 $ K = $ $ {\text{0}}{\text{.1085}} $ ， $ T = {\text{9}}{\text{.9447}} $ ，选择PID参数为 $ {k_p} = 10.27 $ ， $ {k_i} = $ $ 0.34 $ ， $ {k_d} = 45.99 $ 。

本文算法的仿真参数为 $ c = 2 $ ， $ {k_1} = 0.1 $ ， $ {k_2} = 0.01 $ ， $ {\omega _0}{\text{ = }}0.1 $ 。

设置2种仿真环境：无风浪情况下与3级海况情况下进行航迹跟踪控制。

4.1 无风浪环境

为了验证本文算法在存在模型辨识误差与模型非线性项时的控制性能，在无风浪环境下对本文算法与PID控制算法进行对比仿真实验，仿真结果如下：

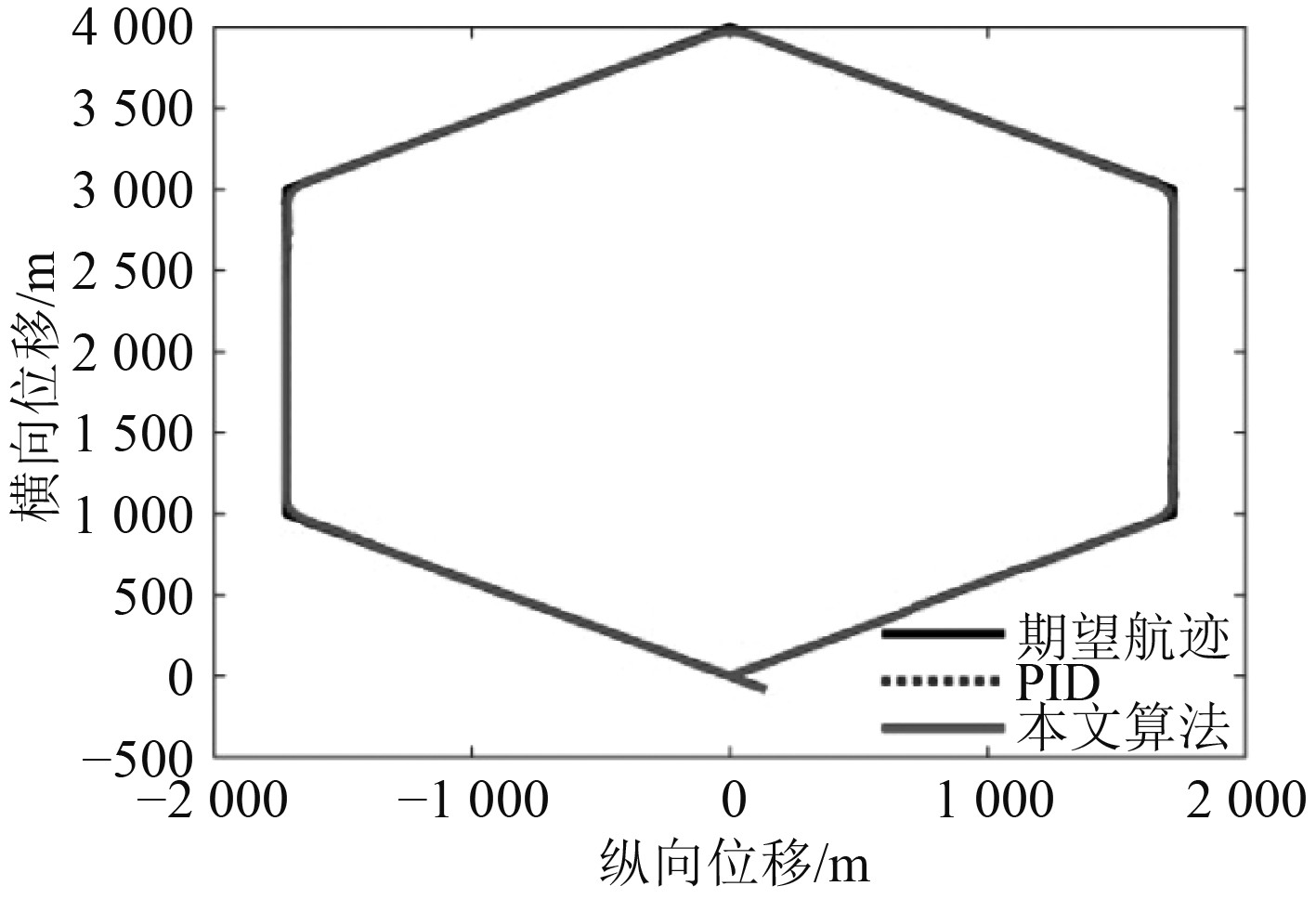
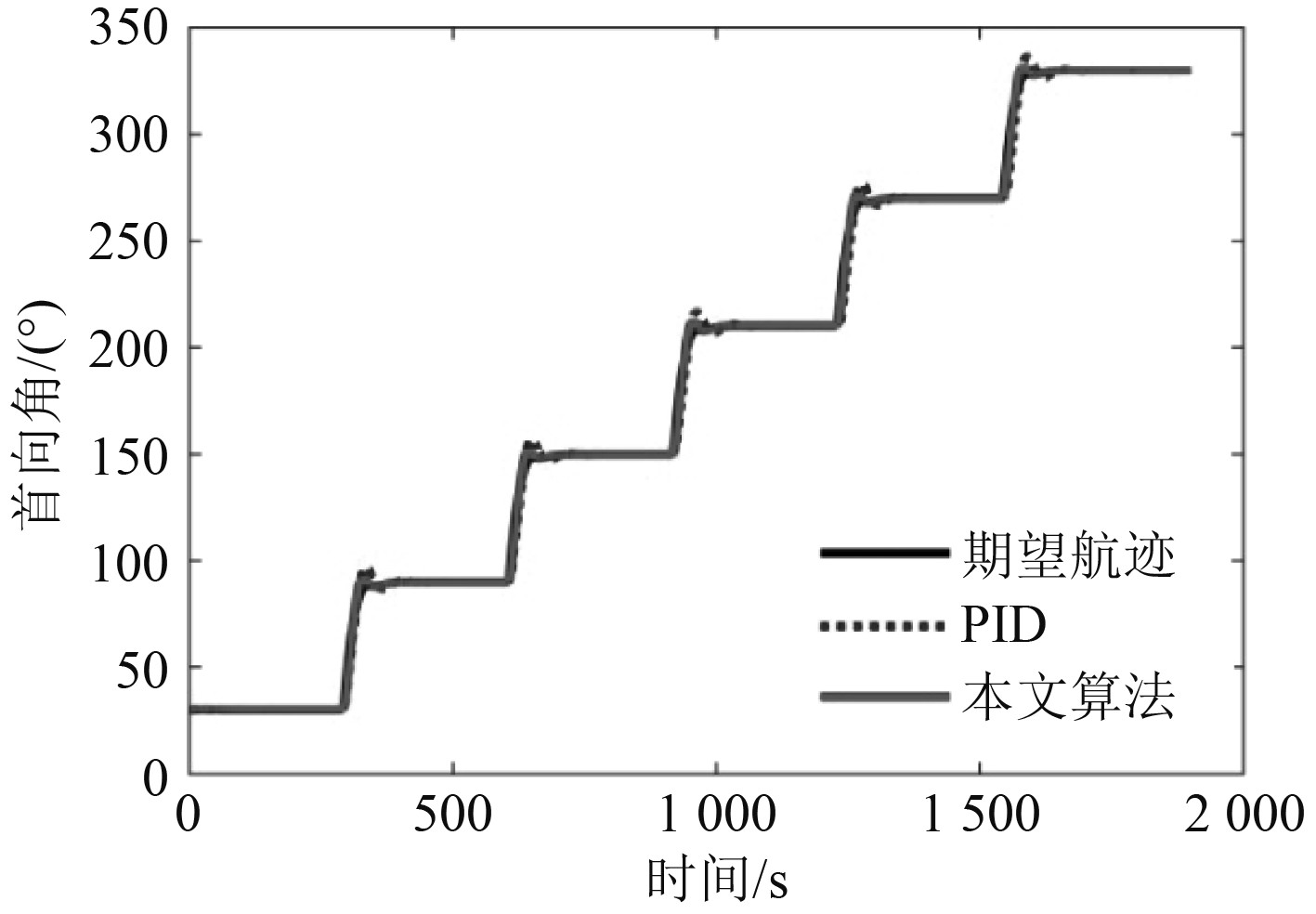
图2与图3分别为航迹跟踪控制与航向控制曲线。可以看出，本文算法与PID算法均能有效地控制船舶的航向与航迹。

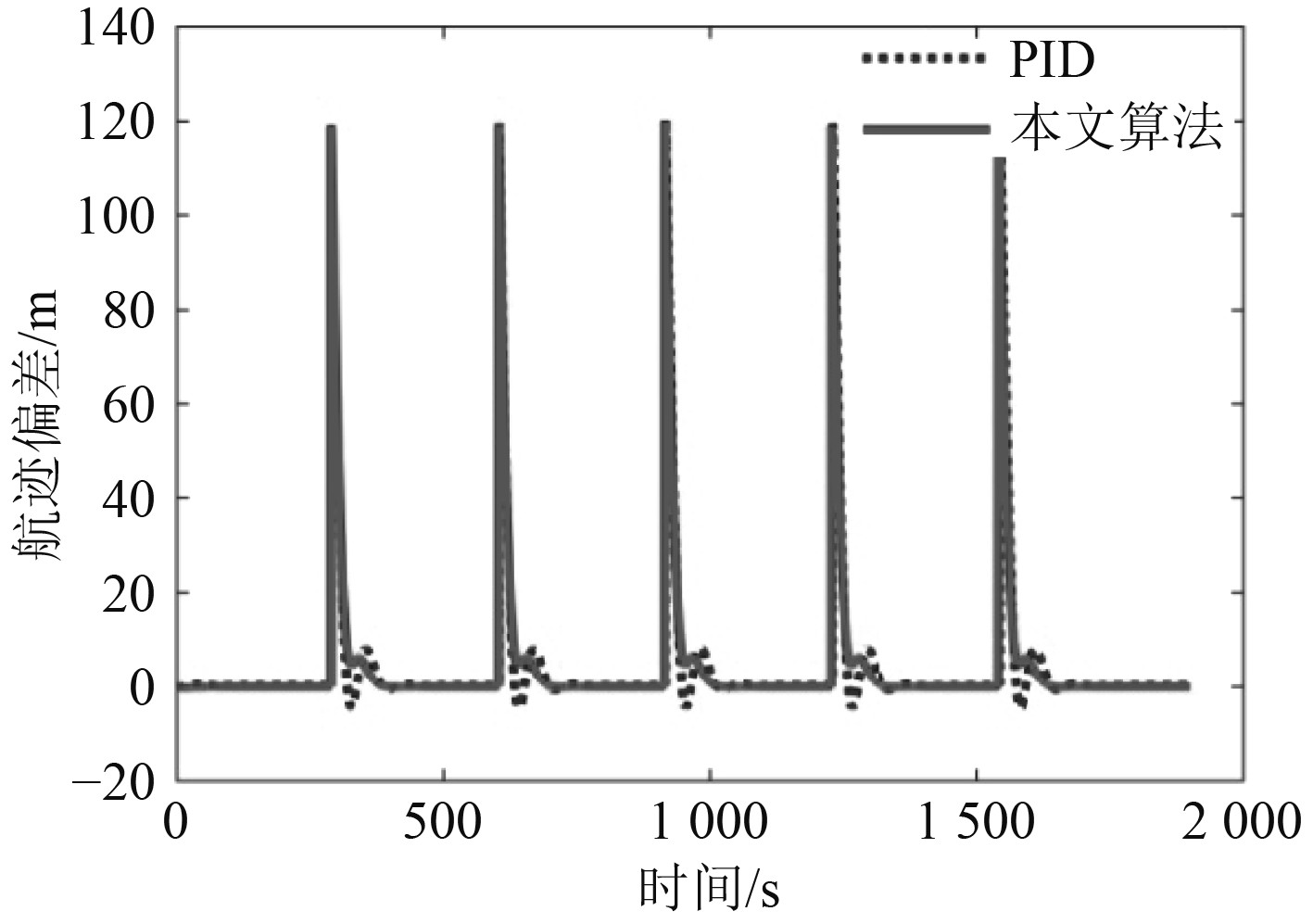
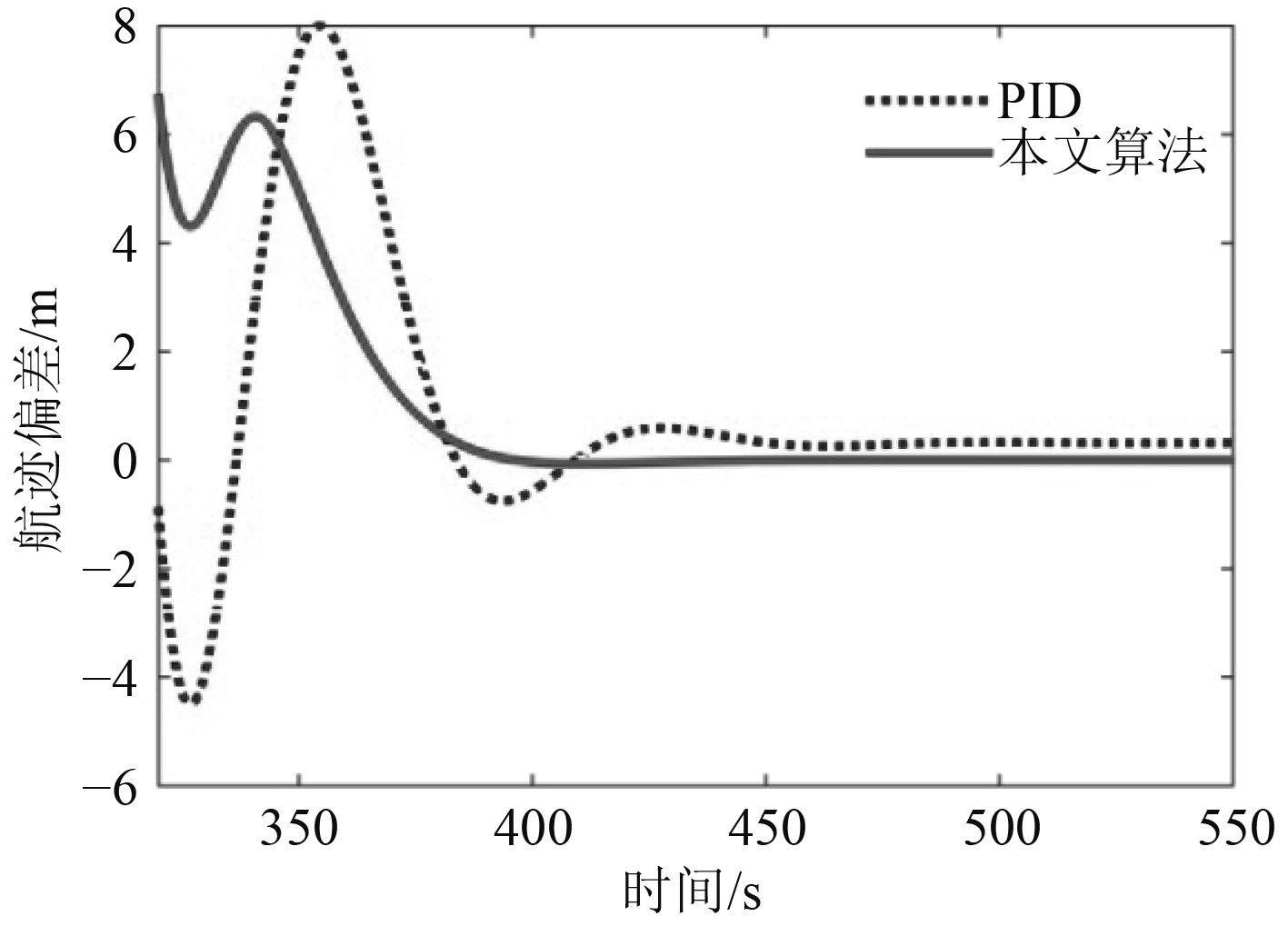
图4为船舶的航迹偏差曲线。可以看出，除在航迹切换点控制偏差较大外，2种控制算法均能够使航迹偏差保持在较小范围内，符合航迹跟踪控制要求。320～550 s内的局部航迹偏差图如图5所示。可以看出，相比与传统PID控制器，本文设计的控制器能够使航迹偏差更快收敛，并且航迹偏差稳态值接近于0，而PID的航迹偏差稳态值约为0.3 m，说明本文算法能够有效地提高船舶航迹追踪控制精度。

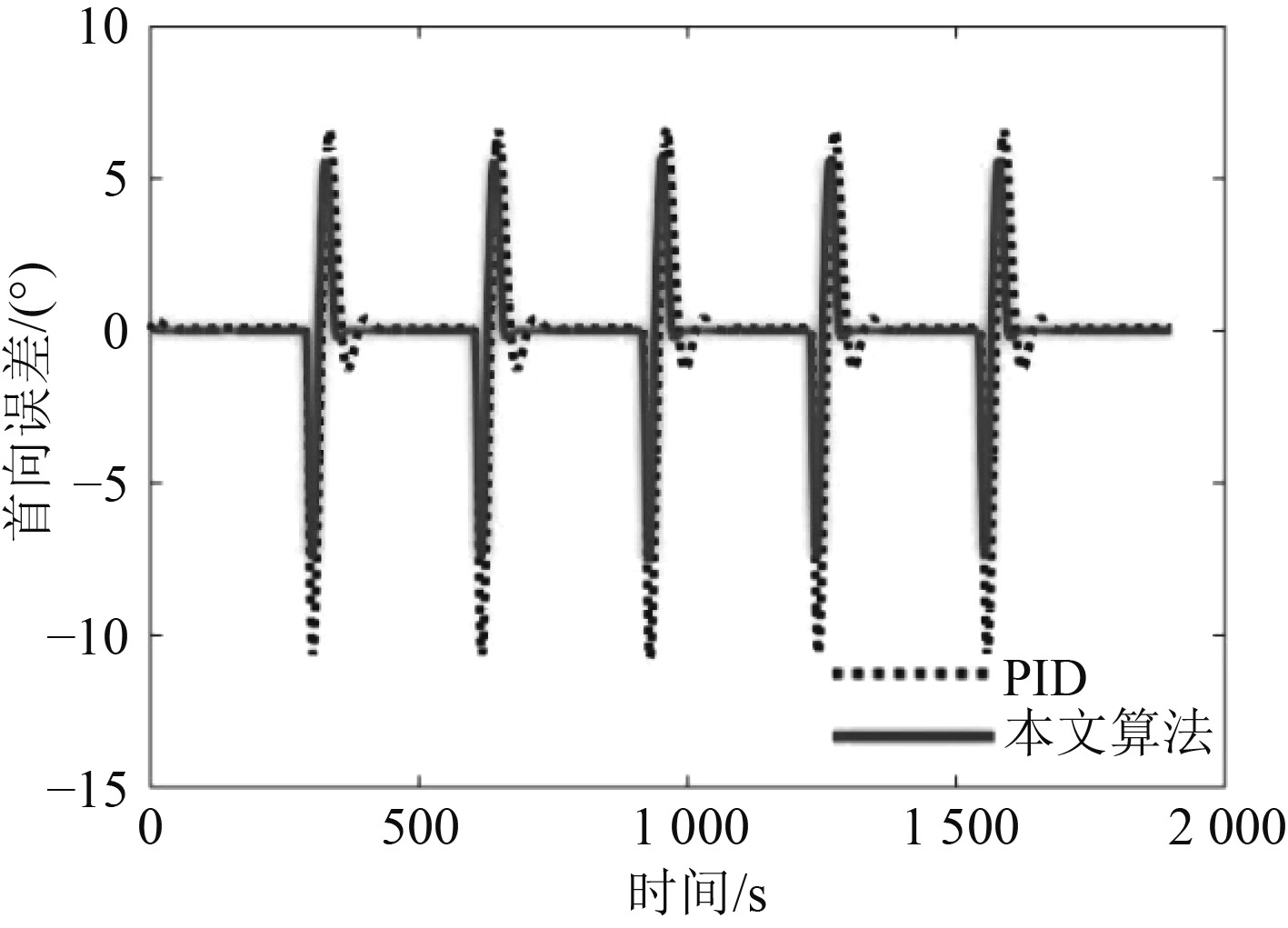
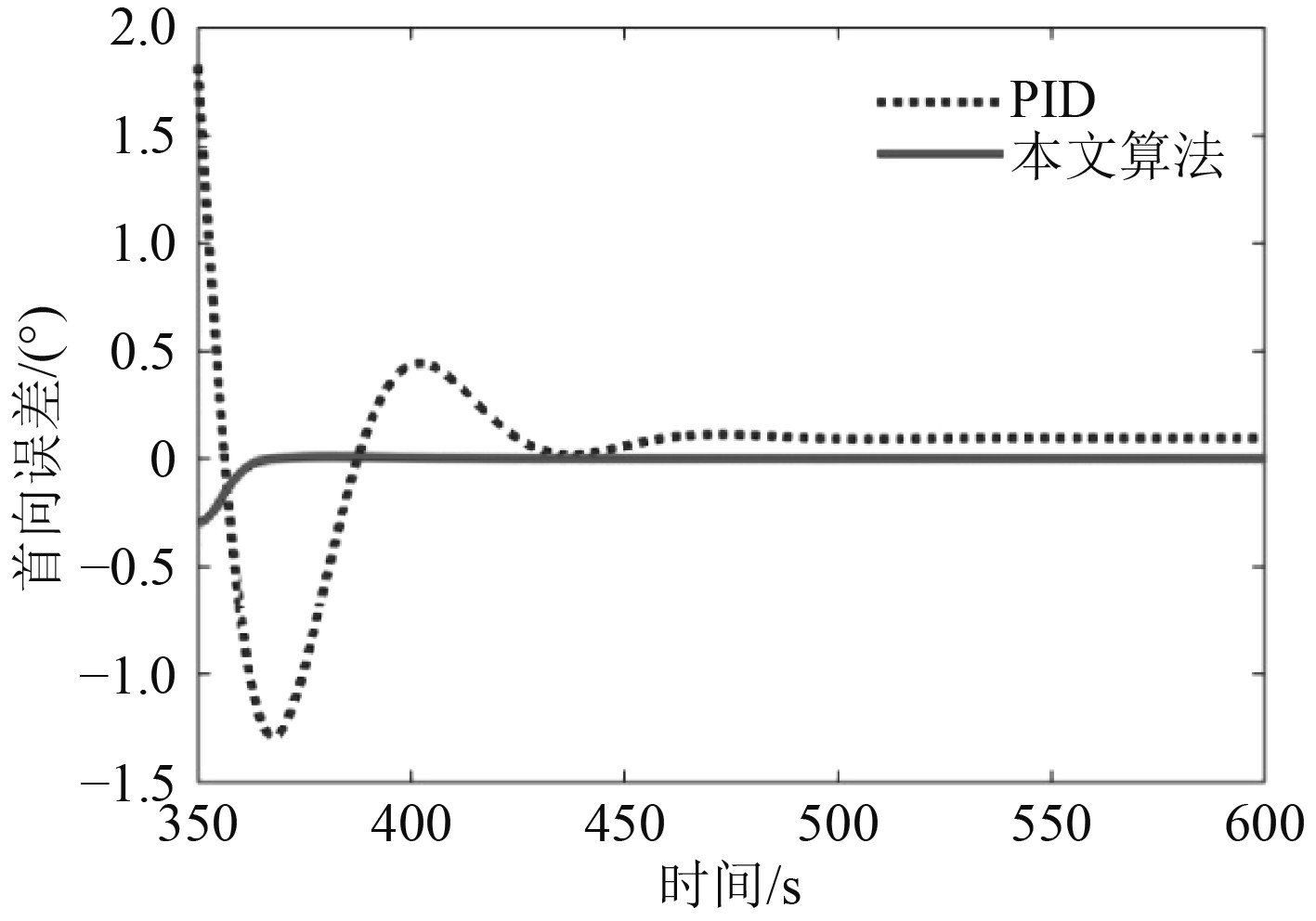
图6为船舶的首向跟踪误差曲线图，图7为350～600 s的首向误差局部放大图。可以看出：相比与PID控制器，本文的控制算法能够使船舶首向快速收敛到稳态值，且振荡次数较少；稳态首向误差接近于0，说明本文算法能够有效提高首向控制精度。

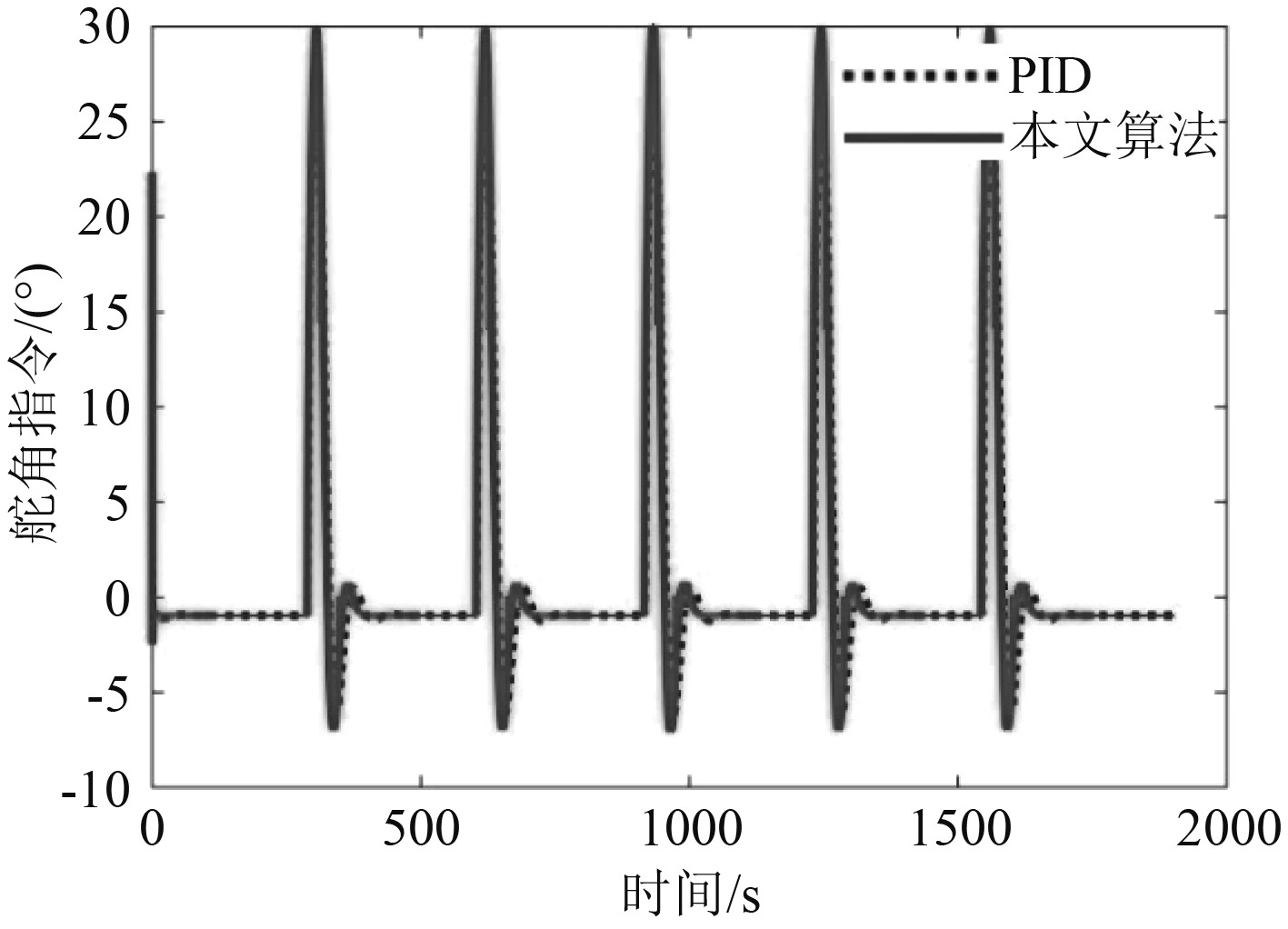
图8为2种控制器输出的舵角指令曲线图。可知本文算法的舵角曲线变化趋势与PID控制算法相同，且没有出现频繁的打舵现象，说明本文算法可以在不增加舵机负担的前提下有效的提高航迹跟踪的控制精度。

4.2 3级海况环境

为了验证本文算法对外部风浪干扰的鲁棒性，设置3级海况的仿真环境：风向为0°，海浪的有义波高为1.25 m。对本文算法与PID算法进行仿真验证，仿真结果如图9和图10所示。

可以看出，相比于PID控制器，本文设计的控制器能够提高航迹追踪与首向控制的控制精度，提高船舶对外界风浪干扰的鲁棒性。为了定量分析本文算法对航迹与航向控制精度的提升，使用均方差（MSE）作为衡量指标。为了消除航迹点切换时大的航迹偏差对航迹偏差均方差的影响，在计算航迹偏差均方差去掉航迹偏差调整的时段，则2种控制器的航迹偏差与首向误差的均方差如表1所示。

分析可知，相比于PID控制器，本文算法使船舶的航迹偏差均方差与航向误差均方差分别下降了65.7%和81.6%，说明本文算法能够明显提高船舶航迹追踪与首向控制精度，增强对风浪干扰的鲁棒性。

5 结　语

针对船舶在3级海况下的航迹追踪控制问题，提出一种基于Super-twisting的滑模自抗扰控制方法。该方法将线性扩张观测器与Super-twisting 2阶滑模控制结合来进行船舶的航迹控制，具有航迹控制精度高、抗风浪干扰能力强、调节参数少的优点。与PID的对比实验证明，本文算法能够有效地提高船舶航迹追踪控制精度，增强对风浪干扰的鲁棒性。