潜水器在海洋探索等方面应用广泛,潜水器能够进行实地考察、取样和测绘等作业。随着深海作业的进一步发展,潜水器正在向深海方向发展[1]。
深海潜水器动力学方程是复杂的非线性微分方程组,目前通用的是美国海军舰船研究与发展中心于1967年提出的潜艇六自由度运动方程[2]。文献[3]利用深海载人潜水器的三自由度的动力学模型对潜浮运动仿真计算,验证其潜浮性能;文献[4]对某潜水器的空间螺旋下潜运动进行模拟,但并未对运动过程中水动力进行详细分析。
深海作业潜水器外形复杂,模型非线性强。本文以某深海潜水器为研究对象,建立六自由度运动模型,基于C++自编程序解算潜水器运动方程,对回转运动和定深下的回转运动分别进行仿真研究。
1 深海潜水器六自由度模型研究深海潜水器六自由度运动时,通常采用通用坐标系,建立2个坐标系:一个定义O-XYZ为惯性坐标系,其固定于地球,又称地球坐标系;另一个定义o-xyz为随体坐标系,其固定于潜水器。通过惯性坐标系与潜水器坐标系的转换,可得到潜水器的空间运动学模型[5]。
把潜水器看作为一个刚体,对潜水器进行受力分析,采用动量定理和动量矩定理[6],得到潜水器空间六自由度方程组:
| $ \begin{split} \left\{ {\begin{array}{*{20}{c}} {m\left[ {\dot u - vr + wq - {x_G}\left( {{q^2} + {r^2}} \right) + {y_G}\left( {pq - \dot r} \right) + {z_G}\left( {pr + \dot q} \right)} \right] = \displaystyle\sum\limits_{{i}} {{X_i}} } ,\\ {m\left[ {\dot v - wp + ur - {y_G}\left( {{r^2} + {p^2}} \right) + {z_G}\left( {qr - \dot p} \right) + {x_G}\left( {qp + \dot r} \right)} \right] = \displaystyle\sum\limits_{{i}} {{Y_i}} } ,\\ {m\left[ {\dot w - uq + vp - {z_G}\left( {{p^2} + {q^2}} \right) + {x_G}\left( {rp - \dot q} \right) + {y_G}\left( {rq + \dot p} \right)} \right] = \displaystyle\sum\limits_{{i}} {{Z_i}} } ,\\ \begin{gathered} {I_x}\dot p + \left( {{I_z} - {I_y}} \right)qr + m\left[ {{y_G}\left( {\dot w + pv - qu} \right) - {z_G}\left( {\dot v + ru - pw} \right)} \right] - ,\\ \left( {\dot r + pq} \right){I_{xz}} + \left( {{r^2} - {q^2}} \right){I_{yz}} + \left( {pr - \dot q} \right){I_{xy}} = \sum\limits_{{i}} {{K_i}} ,\\ \end{gathered} \\ \begin{gathered} {I_y}\dot q + \left( {{I_x} - {I_z}} \right)rp + m\left[ {{z_G}\left( {\dot u + qw - rv} \right) - {x_G}\left( {\dot w + pv - qu} \right)} \right] - ,\\ \left( {\dot p + qr} \right){I_{xy}} + \left( {{p^2} - {r^2}} \right){I_{xz}} + \left( {qp - \dot r} \right){I_{yz}} = \sum\limits_{{i}} {{M_i}} ,\\ \end{gathered} \\ \begin{gathered} {I_z}\dot r + \left( {{I_y} - {I_x}} \right)pq + m\left[ {{x_G}\left( {\dot v + ru - pw} \right) - {y_G}\left( {\dot u + qw - rv} \right)} \right] - ,\\ \left( {\dot q + rp} \right){I_{yz}} + \left( {{q^2} - {p^2}} \right){I_{xy}} + \left( {rq - \dot p} \right){I_{xz}} = \sum\limits_{{i}} {{N_i}}。\end{gathered} \end{array}} \right. \end{split} $ | (1) |
其中,外力和外力矩包括螺旋桨推力、水动力、重力和浮力及力矩等,对于外力和外力矩建模可参考文献[7],其中六自由度外力模型如下:
| $ \begin{split} \sum\limits_{{i}} {{X_i}} = &\frac{1}{2}\rho {L^4}\left[ {X_{qq}^{'}{q^2} + X_{rr}^{'}{r^2} + X_{pr}^{'}pr} \right] + \frac{1}{2}\rho {L^3}\left[ X_{\dot u}^{'}\dot u +\right.\\ &\left.X_{vr}^{'}vr + X_{wq}^{'}wq \right] + \frac{1}{2}\rho {L^2}\left[ X_{uu}^{'}{u^2} + X_{vv}^{'}{v^2} + \right.\\ &\left.X_{ww}^{'}{w^2} + X_{uw}^{'}uw \right] - \left( {W - B} \right)\sin \theta + {X_T},\end{split} $ | (2) |
| $ \begin{split} \sum\limits_{{i}} {{Y_i}} =& \frac{1}{2}\rho {L^4}\left[ {Y_{\dot r}^{'}\dot r + Y_{\dot p}^{'}\dot p + Y_{r\left| r \right|}^{'}r\left| r \right| + Y_{p\left| p \right|}^{'}p\left| p \right| + Y_{pq}^{'}pq + Y_{qr}^{'}qr} \right] + \\ & \frac{1}{2}\rho {L^3}\left[ {Y_{\dot v}^{'}\dot v + Y_p^{'}up + Y_r^{'}ur + Y_{vq}^{'}vq + Y_{wp}^{'}wp + Y_{wr}^{'}wr} \right] + \\ & \frac{1}{2}\rho {L^3}\left[ {Y_{v\left| r \right|}^{'}\frac{v}{{\left| v \right|}}\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|\left| r \right| + Y_{vww}^{'}v{w^2}} \right] +\\ &\frac{1}{2}\rho {L^2}\left[ {Y_0^{'}{u^2} + Y_v^{'}uv + Y_{vw}^{'}vw} \right] + \\ &\frac{1}{2}\rho {L^2}Y_{v\left| v \right|}^{'}v\left| {{{\left( {{v^2} + {w^2}} \right)}^{\frac{1}{2}}}} \right| + \\ & \left( {W - B} \right)\cos \theta \sin \phi + {Y_T} ,\\[-15pt] \end{split} $ | (3) |
| $ \begin{split} \sum\limits_{{i}} {{Z_i}} = & \frac{1}{2}\rho {L^4}\left[ {Z_{\dot q}^{'}\dot q + Z_{q\left| q \right|}^{'}q\left| q \right| + Z_{pp}^{'}{p^2} + Z_{rr}^{'}{r^2} + Z_{rp}^{'}rp} \right] +\\[-3pt] &\frac{1}{2}\rho {L^3}\left[ {Z_{\dot w}^{'}\dot w + Z_{vr}^{'}vr + Z_{vp}^{'}vp + Z_q^{'}uq} \right] +\\ & \frac{1}{2}\rho {L^3}Z_{w\left| q \right|}^{'}\frac{w}{{\left| w \right|}}\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|\left| q \right| + \\ &\frac{1}{2}\rho {L^2}\left[ {Z_0^{'}{u^2} + Z_w^{'}uw + Z_{\left| w \right|}^{'}u\left| w \right| + Z_{vv}^{'}{v^2} + Z_{\left| v \right|w}^{'}\left| v \right|w} \right]+ \\ & \frac{1}{2}\rho {L^2}\left[ {Z_{ww}^{'}\left| {w{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right| + Z_{w\left| w \right|}^{'}w\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|} \right] +\\ &\left( {W - B} \right)\cos \theta {s} \cos \phi + {Z_T} ,\\[-10pt] \end{split} $ | (4) |
| $ \begin{split} \sum\limits_{{i}} {{K_i}} = &\frac{1}{2}\rho {L^5}\left[ K_{\dot r}^{'}\dot r + K_{\dot p}^{'}\dot p + K_{r\left| r \right|}^{'}r\left| r \right| + K_{p\left| p \right|}^{'}p\left| p \right| + K_{pq}^{'}pq +\right.\\[-3pt] &\left.Z_{qr}^{'}qr \right] + \frac{1}{2}\rho {L^4}\left[ {K_{\dot v}^{'}\dot v + K_{vq}^{'}vq + K_{wp}^{'}wp + K_{wr}^{'}wr} \right] + \\ &\frac{1}{2}\rho {L^4}\left[ {K_r^{'}ur + K_p^{'}up + K_{vww}^{'}v{w^2}} \right] + \frac{1}{2}\rho {L^3}\left[ K_0^{'}{u^2} +\right. \\ & \left.K_v^{'}uv + K_{v\left| v \right|}^{'}v\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right| + K_{vw}^{'}vw \right] + ( {y_G}W -\\ & {y_C}B )\cos \theta \cos \phi -\left( {{z_G}W - {z_C}B} \right)\cos \theta \sin \phi + {K_T} ,\\[-10pt] \end{split} $ | (5) |
| $ \begin{split} \sum\limits_{{i}} {{M_i}} = & \frac{1}{2}\rho {L^5}\left[ {M_{\dot q}^{'}\dot q + M_{q\left| q \right|}^{'}q\left| q \right| + M_{pp}^{'}{p^2} + M_{rr}^{'}{r^2} + M_{rp}^{'}rp} \right] +\\[-3pt] & \frac{1}{2}\rho {L^4}\left[ M_{\dot w}^{'}\dot w + M_{vr}^{'}vr + M_{vp}^{'}vp + M_q^{'}uq + \right.\\ &\left.M_{\left| w \right|q}^{'}{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}q \right] + \frac{1}{2}\rho {L^3}\left[ M_0^{'}{u^2} + M_w^{'}uw +\right.\\ &\left. M_{w\left| w \right|}^{'}w\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right| +M_{vv}^{'}{v^2} + M_{\left| w \right|}^{'}u\left| w \right| \right] + \\ \begin{array}{*{20}{c}} \end{array} & \frac{1}{2}\rho {L^3}M_{ww}^{'}\left| {w{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right| - \left( {x_G}W -\right.\\ &\left. {x_C}B \right)\cos \theta \cos \phi - \left( {z_G}W - {z_C}B \right)\sin \theta + {M_T} ,\\[-15pt] \end{split} $ | (6) |
| $ \begin{split} \sum\limits_{{i}} {{N_i}} =& \frac{1}{2}\rho {L^5}\left[ {N_{\dot r}^{'}\dot r + N_{\dot p}^{'}\dot p + N_{pq}^{'}pq + N_{qr}^{'}qr} \right] + \\[-3pt] &\frac{1}{2}\rho {L^5}\left[ {N_{r\left| r \right|}^{'}r\left| r \right| + N_{p\left| p \right|}^{'}p\left| p \right|} \right]+ \frac{1}{2}\rho {L^4}\left[ N_{\dot v}^{'}\dot v + \right.\\ &\left. N_{wr}^{'}wr + N_{wp}^{'}wp + N_{vq}^{'}vq + N_{vww}^{'}v{w^2} + N_r^{'}ur + N_p^{'}up \right] + \\ & \frac{1}{2}\rho {L^4}N_{\left| v \right|r}^{'}\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|r + \frac{1}{2}\rho {L^3}\left[ N_0^{'}{u^2} + N_v^{'}uv +\right.\\ &\left.N_{v\left| v \right|}^{'}v\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right| + N_{vw}^{'}vw \right]+ \left( {x_G}W -\right. \\ &\left. {x_C}B \right)\cos \theta \sin \phi + \left( {{y_G}W - {y_C}B} \right)\sin \theta + {N_T} 。\\[-10pt] \end{split} $ | (7) |
本文的潜水器对象为某深海潜水器,水动力系数的来源是风洞和旋臂水池中的模型试验。
2 深海潜水器运动仿真软件深海潜水器六自由度模型运动方程是一个12个方程和12个变量的微分方程组,该方程组是隐式的,进行变换,可得其显式形式。如果给定初始状态和推力大小,可对显式微分方程组进行求解,根据动力学模型和运动学模型,可实现对深海潜水器运动的模拟仿真。
3 运动仿真研究 3.1 空间回转运动仿真推进器的输入推力:T=[560 N,422.7 N,0,0,0,1197.5 N·m]T;初始航速为1 kn,深度在6 000 m,潜水器进行正航回转运动,仿真结果如图1~图8所示。

|
图 1 空间回转轨迹 Fig. 1 Spatial rotation trajectory |

|
图 2 水平面投影 Fig. 2 Horizontal plane projection |

|
图 3 空间回转u-t Fig. 3 Spatial rotation u-t |

|
图 4 空间回转v-t Fig. 4 Spatial rotation v-t |
|
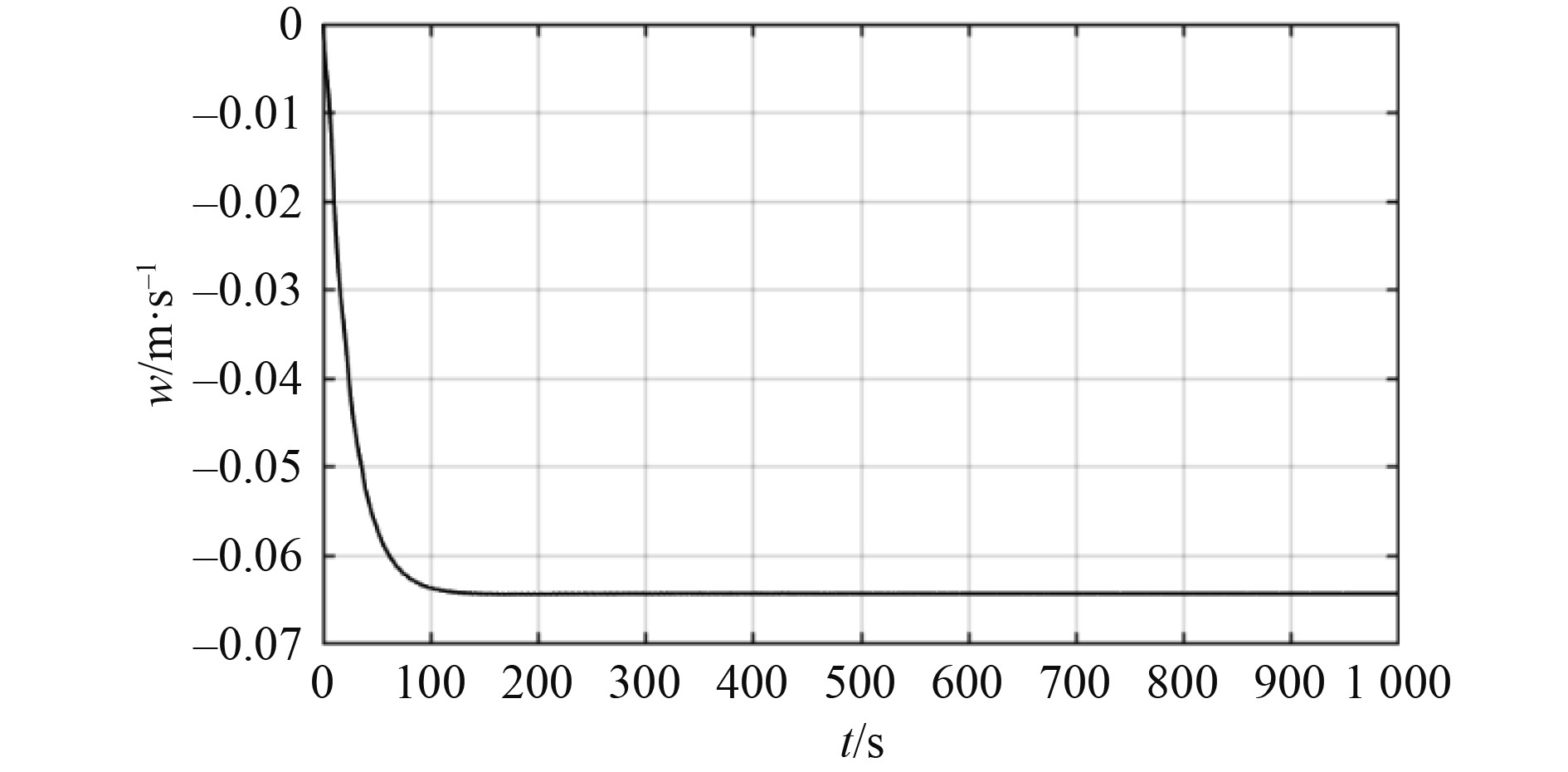
图 5 空间回转w-t Fig. 5 Spatial rotation w-t |

|
图 6 空间回转ϕ-t Fig. 6 Spatial rotation ϕ-t |
|
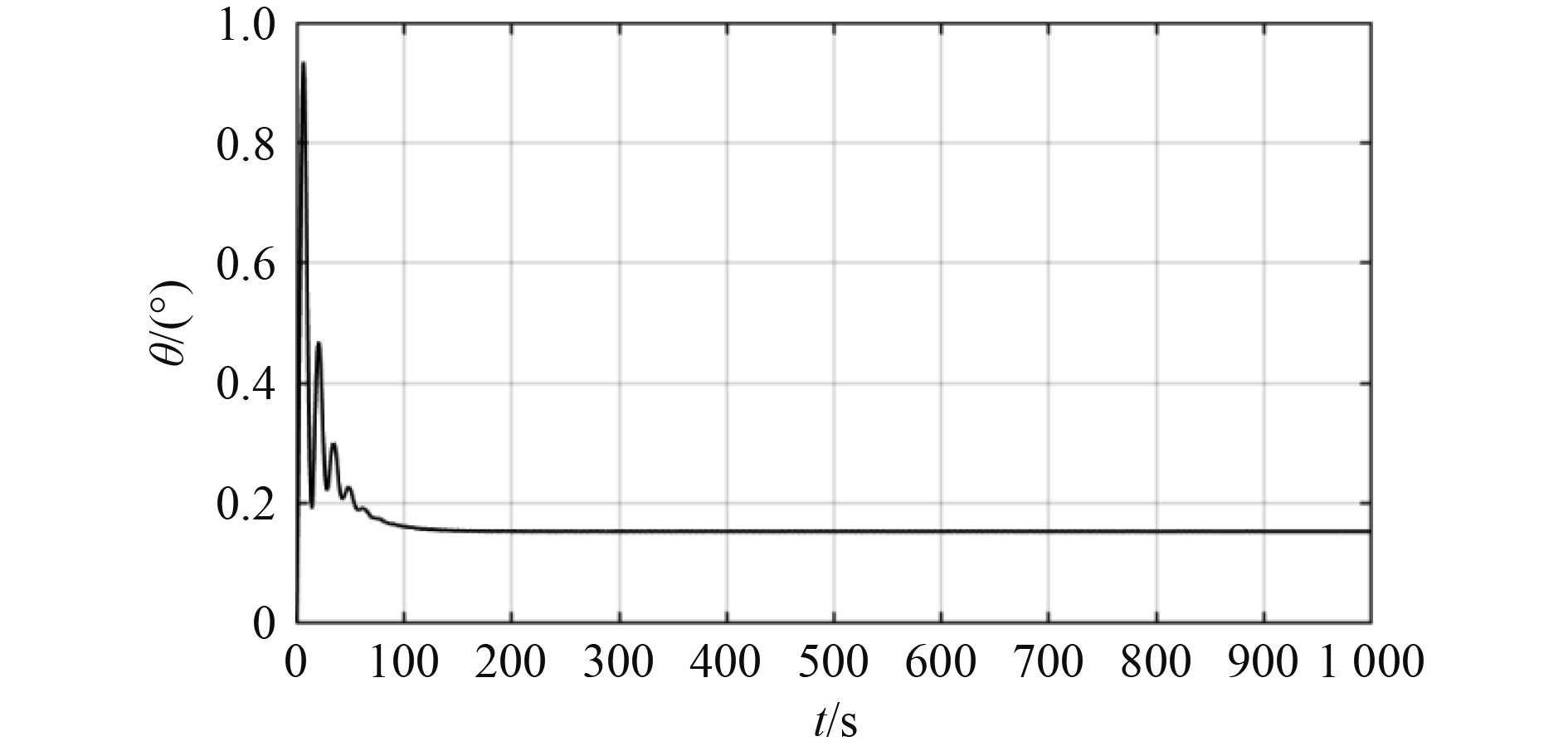
图 7 空间回转θ-t Fig. 7 Spatial rotation θ-t |
|
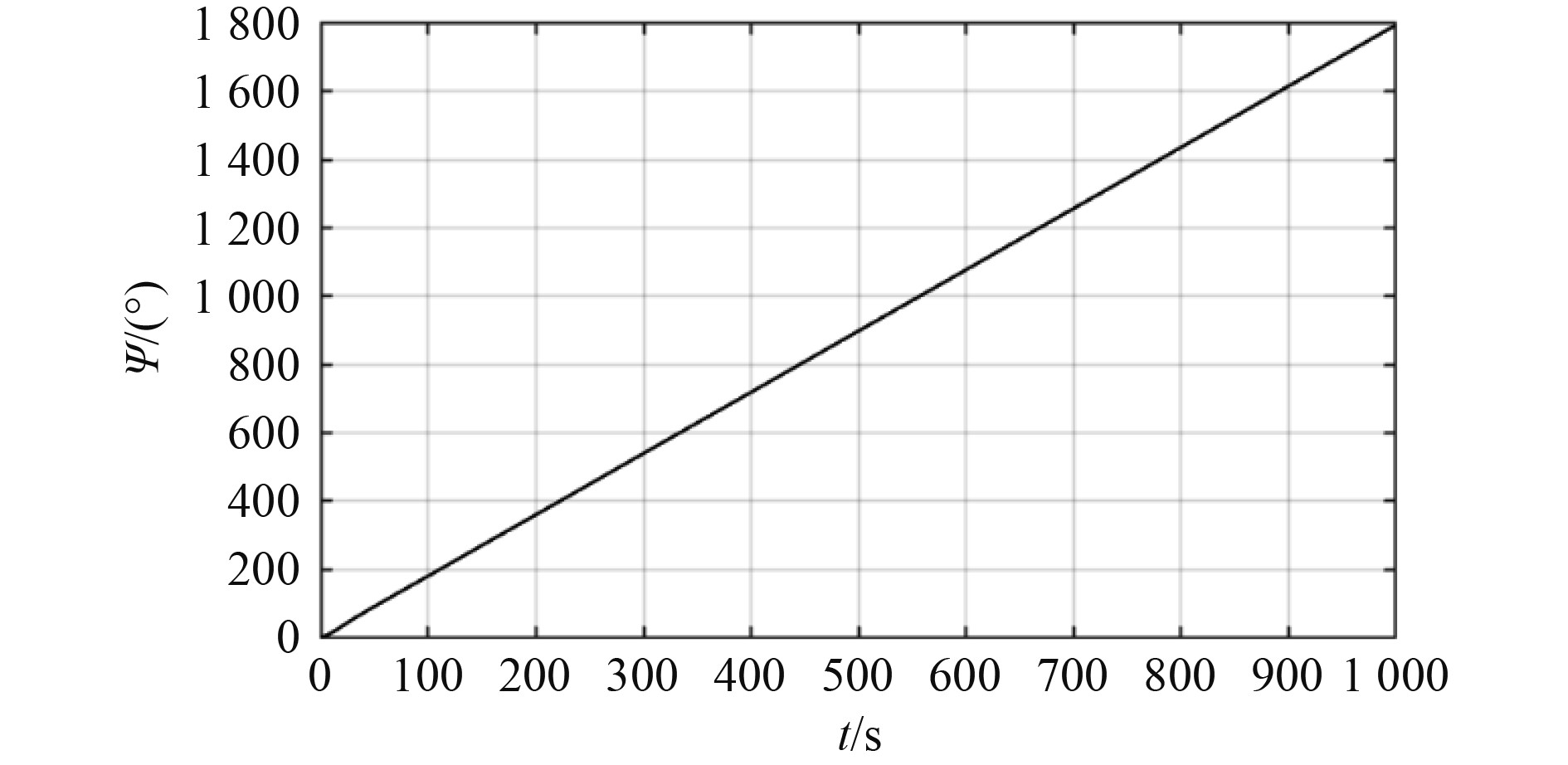
图 8 空间回转ψ-t Fig. 8 Spatial rotation ψ-t |
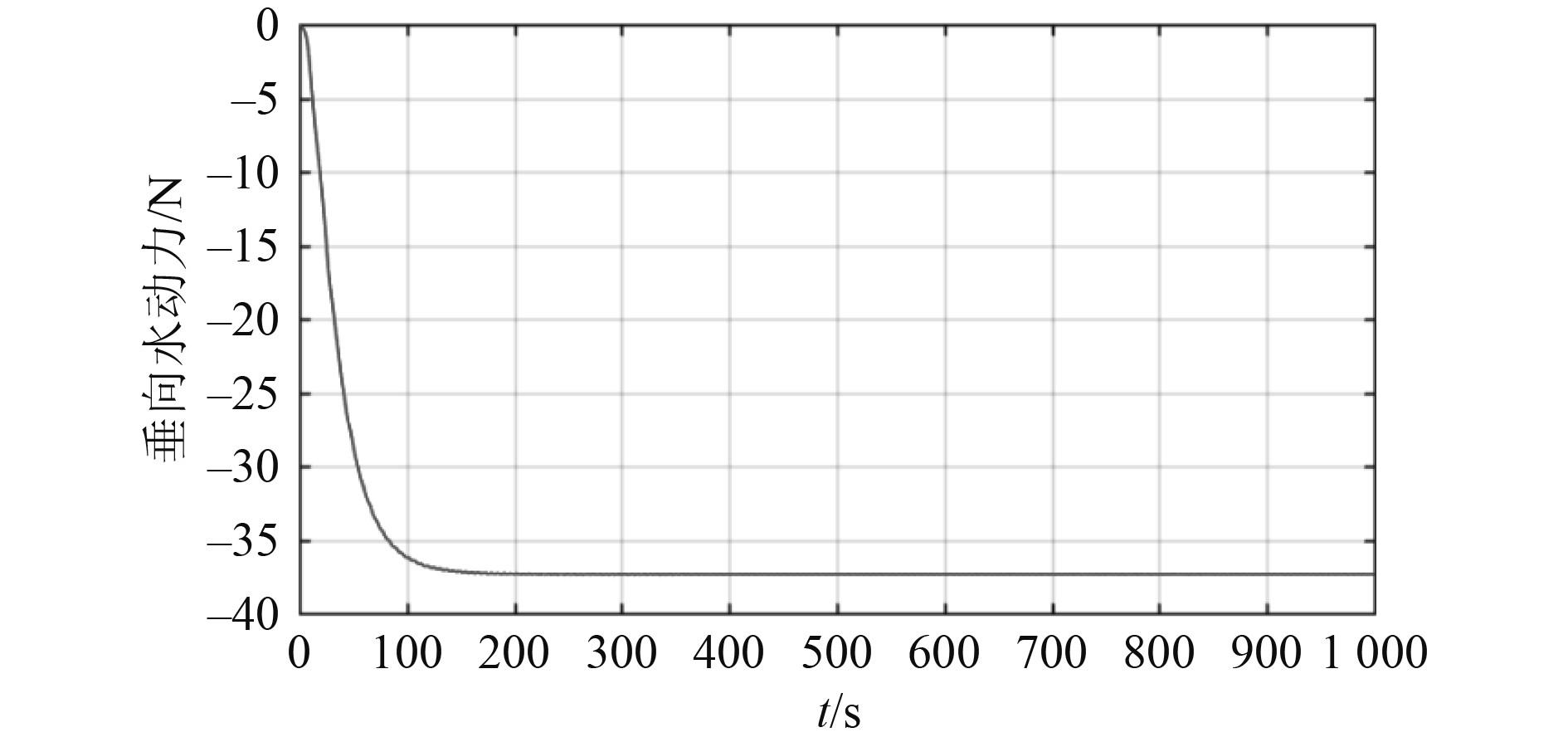
可知,潜水器做空间回转运动,回转运动的直径为32 m,在t=200 s以后,纵向速度为0.495 m/s,垂向升速为0.064 m/s,横向速度很小,横向速度对回转运动影响可忽略不计。潜器垂向水动力仿真结果如图9所示。
|
图 9 潜器垂向水动力 Fig. 9 Vertical hydrodynamic force of submersible |
深潜器上下外形的不对称导致产生垂向的水动力,因而做空间回转运动。为保证潜器进行水平面作业,在进行回转运动的同时,开启自动定深功能,仿真结果如图10~图12所示。
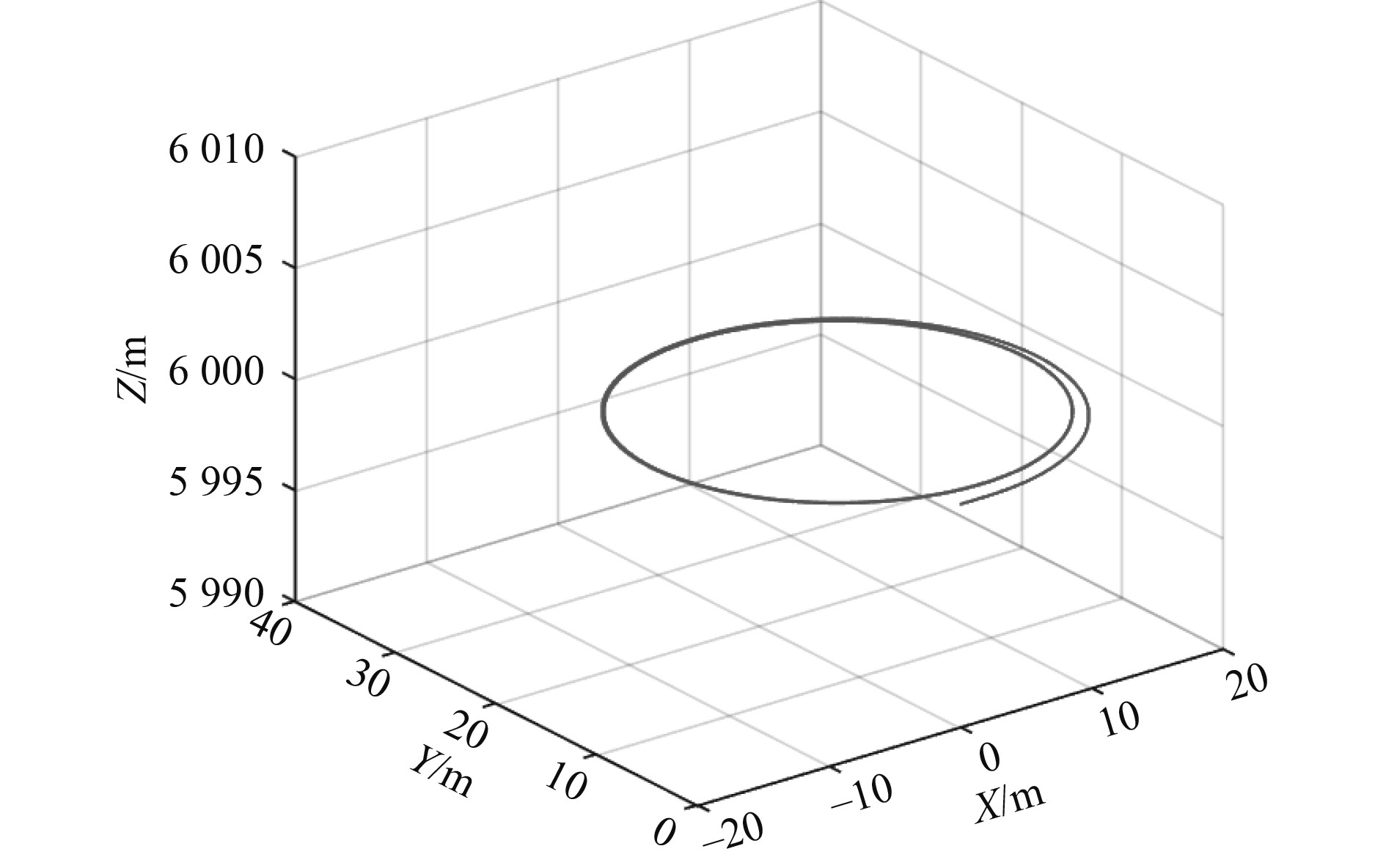
|
图 10 定深下的回转轨迹 Fig. 10 Rotation track under fixed depth control |
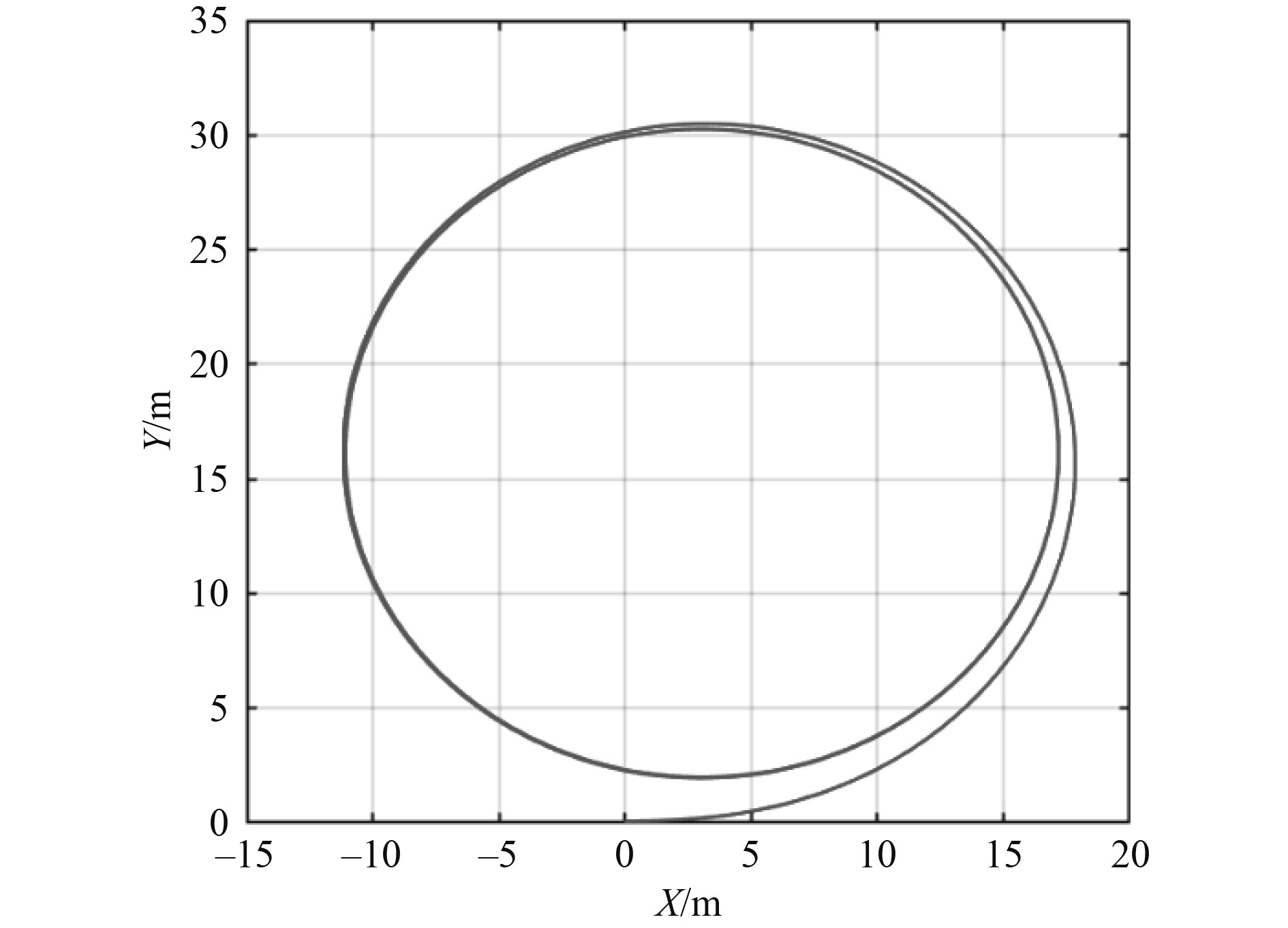
|
图 11 水平面投影 Fig. 11 Horizontal projection |
从仿真结果看,潜水器做水平面回转运动,回转运动的直径为28.5 m,定深状态下的回转半径相对较小。
3.3 结果分析
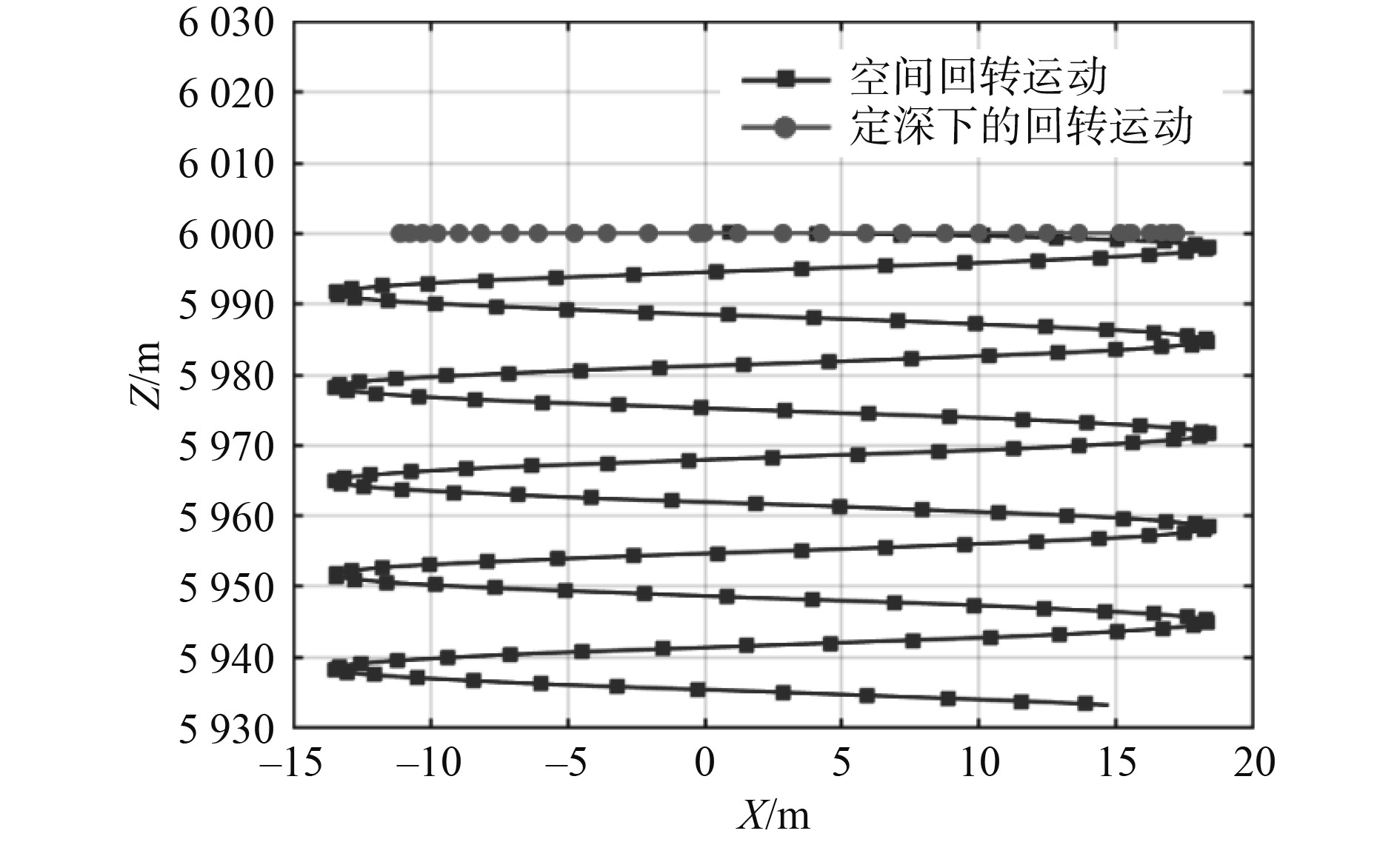
|
图 12 垂直面投影对比图 Fig. 12 Comparison of vertical plane projection |
1)深潜器回转时,做空间运动,在轨迹上看作为螺旋运动。由于潜器上下不对称导致产生向上的微小水动力,而且垂向水动力具有很强的非线性,导致做空间回转运动。
2)该深潜器回转运动运动半径不大,反映深潜器的机动性很好。同时,定深状态下的回转半径相对较小,反映出垂向诱导水动力对回转半径的干扰影响。
3)通过自动定深控制,深潜器能够较好地完成水平面回转运动作业。
4 结 语本文首先给出深海潜水器六自由度模型,通过C++自编程序解算潜水器运动方程,对回转运动进行仿真。结果表明:该深潜器具备良好的空间机动性,潜器上下不对称导致产生向上的水动力,进而导致潜水器做空间运动,且垂向水动力具有很强的非线性;通过自动定深控制,深潜器能够较好地完成水平面回转运动作业。
| [1] |
姜哲, 崔维成. 全海深潜水器水动力学研究最新进展[J]. 中国造船, 2015, 56(4): 188-199. DOI:10.3969/j.issn.1000-4882.2015.04.020 |
| [2] |
GERTLER M, HAGEN G R. Standard equations of motion for submarine simulation[J]. Standard Equations of Motion for Submarine Simulation, 1967.
|
| [3] |
马岭, 崔维成. 载人潜水器潜浮运动的模拟[J]. 船舶力学, 2004(3): 31−38.
|
| [4] |
孙晓芳. 某智能潜水器操纵性能分析和运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [5] |
魏延辉. UVMS系统控制技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2017.
|
| [6] |
谢俊元. 深海载人潜水器动力学建模研究及操纵仿真器研制[D]. 无锡: 江南大学, 2009.
|
| [7] |
孙元泉. 潜艇和深潜器的现代操纵理论与应用[M]. 北京: 国防工业出版社, 2001.
|
 2022, Vol. 44
2022, Vol. 44
