0 引　言

近年来，自主水下航行器（automatic underwater vehicle，AUV）在海洋探测领域得到了越来越多的应用，尤其在海底地形勘测领域有着重要地位。然而，水下复杂的环境给AUV的控制带来挑战，欠驱动AUV的运动控制成为研究的热点，深度控制是其中一个经典的问题^[1]。

经典的PID控制器在欠驱动AUV的深度控制上应用广泛，神经网络、模糊系统^[2]等被用来优化PID控制器。刘丽萍等^[3]将自适应率引入控制器，得到的自适应反演滑模轨迹跟踪控制器对海流等因素带来的影响进行补偿，避免了对PID参数的整定。

粒子群优化算法（particle swarm optimization，PSO）是一种随机全局优化技术^[4]，其拥有代码量小、易于实现、参数较少等优点。胡坤等^[5]利用PSO对系统的非线性PID控制参数进行优化；针对PSO易陷入局部最优解的问题，杨巍等^[6]提出了动态权值自适应粒子群算法；在此基础上，张继荣等^[7]提出了惯性权重余弦调整的粒子群优化算法（inertial weight cosine particle swarm optimization，IWCPSO），加快了粒子收敛后期的收敛速度。

本文在上述算法的基础上，引入指数函数对PSO的惯性权重进行调整，将改进后的优化算法用于PID的参数优化，并与经典的Ziegler-Nichols(ZN)整定法^[8]进行比较。结果表明，改进后的PSO兼顾了收敛速度和精度，表现更佳。

1 欠驱动自主水下航行器建模

本文使用的大地坐标系和载体坐标系分别记作 $ {S}_{E}(E,{X}_{e},{Y}_{e},{Z}_{e}) $ 和 $ {S}_{B}(B,x,y,z) $ ，它们之间的转换由旋转矩阵实现，记作 $ {C}_{B}^{E} $ 和 $ {C}_{E}^{B} $ ，在体坐标系下，规定垂直水平面向上为 $ z $ 轴的正方向。记广义方位矩阵 $ \mathbf{\eta }={[{X}_{e},{Y}_{e},{Z}_{e},\varphi ,\psi ,\theta ]}^{{\rm{T}}} $ ，广义速度矩阵 $ \mathit{v}= {[u,v,w,p,q,r]}^{{\rm{T}}} $ ，广义力矩阵 $ \mathbf{\tau }={[{F}_{x},{F}_{y},{F}_{z},R,M,N]}^{{\rm{T}}} $ ，矩阵中的前3个参数代表大地坐标系下的位置信息，后3个参数代表载体坐标系下的角度信息。由于欠驱动AUV的横向和垂向没有推力，也没有推力使AUV绕体坐标系的 $ x $ 轴旋转，因此上述广义速度矩阵可以简化为 $ \mathit{v}= [u,v, $ $ w,q,r]^{{\rm{T}}} $ ， $ u $ ， $ v $ ， $ w $ 分别表示AUV的速度在体坐标系的 $ x $ ， $ y $ ， $ z $ 轴上的投影， $ q $ 和 $ r $ 分别为AUV绕体坐标系的 $ y $ ， $ z $ 轴的旋转角速度。广义力矩阵可以简化为 $ \mathbf{\tau }= $ $ [{F}_{x},\mathrm{0,0},0,{\delta }_{s},{\delta }_{r}] $ ， $ {F}_{x} $ 代表AUV尾部的推力， $ {\delta }_{s} $ 和 $ {\delta }_{r} $ 分别代表舵机的力矩。

根据牛顿-欧拉方程，欠驱动AUV在载体坐标系下的六自由度动力学方程可表示为：

$ {M}\dot{\mathit{v}}+C\left(\mathit{v}\right)\mathit{v}=\mathit{\tau }+\mathit{\omega } 。$

(1)

其中： $ {M} $ 为广义质量矩阵， $ C\left(\mathit{v}\right) $ 为Corioslis矩阵， $ \mathit{\omega }\in {R}^{6\times 1} $ 为环境干扰项。经推算，欠驱动AUV的非线性微分方程可表示为：

$ \left\{\begin{array}{l}\dot{u}=\dfrac{{m}_{2}}{{m}_{1}}vr-\dfrac{{m}_{3}}{{m}_{1}}wq-\dfrac{{d}_{1}}{{m}_{1}}u+\dfrac{1}{{m}_{1}}{F}_{x}+{\omega }_{1}，\\ \dot{v}=-\dfrac{{m}_{1}}{{m}_{2}}ur-\dfrac{{d}_{2}}{{m}_{2}}v+{\omega }_{2}，\\ \dot{w}=\dfrac{{m}_{1}}{{m}_{3}}uq-\dfrac{{d}_{3}}{{m}_{3}}w+{g}_{1}+{\omega }_{3}，\\ \dot{q}=\frac{{m}_{3}-{m}_{1}}{{m}_{5}}uw-\dfrac{{d}_{4}}{{m}_{5}}q-{g}_{2}+\dfrac{1}{{m}_{5}}{b}_{1}{\delta }_{s}+{\omega }_{4}，\\ \dot{r}=\dfrac{{m}_{1}-{m}_{2}}{{m}_{6}}uv-\dfrac{{d}_{5}}{{m}_{6}}r+\dfrac{1}{{m}_{6}}{b}_{2}{\delta }_{r}+{\omega }_{5}。\end{array}\right. $

(2)

式中： $ {m}_{1}=m-{X}_{\dot{u}}$ ， $ {m}_{2}=m-{Y}_{\dot{v}} $ ， $ {m}_{3}=m-{Z}_{\dot{w}} $ ， ${m}_{5}= {I}_{y}- $ $ {M}_{\dot{q}}$ ， $ {m}_{6}={I}_{z}-{N}_{\dot{r}} $ ， $ {g}_{1}=(W-B)\mathrm{cos}\theta $ ， ${g}_{2}= ({z}_{g}W- {z}_{b}B) $ $ \mathrm{sin}\theta$ ， $ {d}_{1}={X}_{u}+{X}_{u\left|u\right|}\left|u\right| $ ， ${d}_{2}={Y}_{v}+{Y}_{v\left|v\right|}\left|v\right| $ ， ${d}_{3}= {Z}_{w}+ {Z}_{w\left|w\right|} $ $ \left|w\right|$ ， ${d}_{4}={M}_{q}+{M}_{q\left|q\right|}\left|q\right| $ ， ${d}_{5}={N}_{r}+{N}_{r\left|r\right|}\left|r\right| $ ， ${b}_{1}= {u}^{2}{M}_{{\delta }_{s}}$ ， $ b_2= $ $ u^2N_{{\delta }_r} $ 。

其中： $ {m} $ 和 $ {m}_{(\cdot )} $ 分别为AUV的质量和由流体作用产生的附加质量； $ {I}_{(\cdot )} $ 为AUV的绕轴转动惯量； $ {X}_{(\cdot )} $ ， $ {Y}_{(\cdot )} $ ， $ {Z}_{(\cdot )} $ ， $ {M}_{(\cdot )} $ ， $ {N}_{(\cdot )} $ 为粘性流体水动力系数； $ {z}_{g} $ 和 $ {z}_{b} $ 分别为载体坐标系下重心和浮心在 $ {z} $ 轴上的坐标； $ {W} $ 和 $ {B} $ 分别为AUV所受的重力和浮力^[9]，设 $ {w}_{(\cdot )}=0 $ ，忽略环境干扰。

2 PID控制器原理

PID控制器的结构简单，控制原理易于理解，具有很好的鲁棒性，其诸多优点使其成为运用最广的控制器之一。

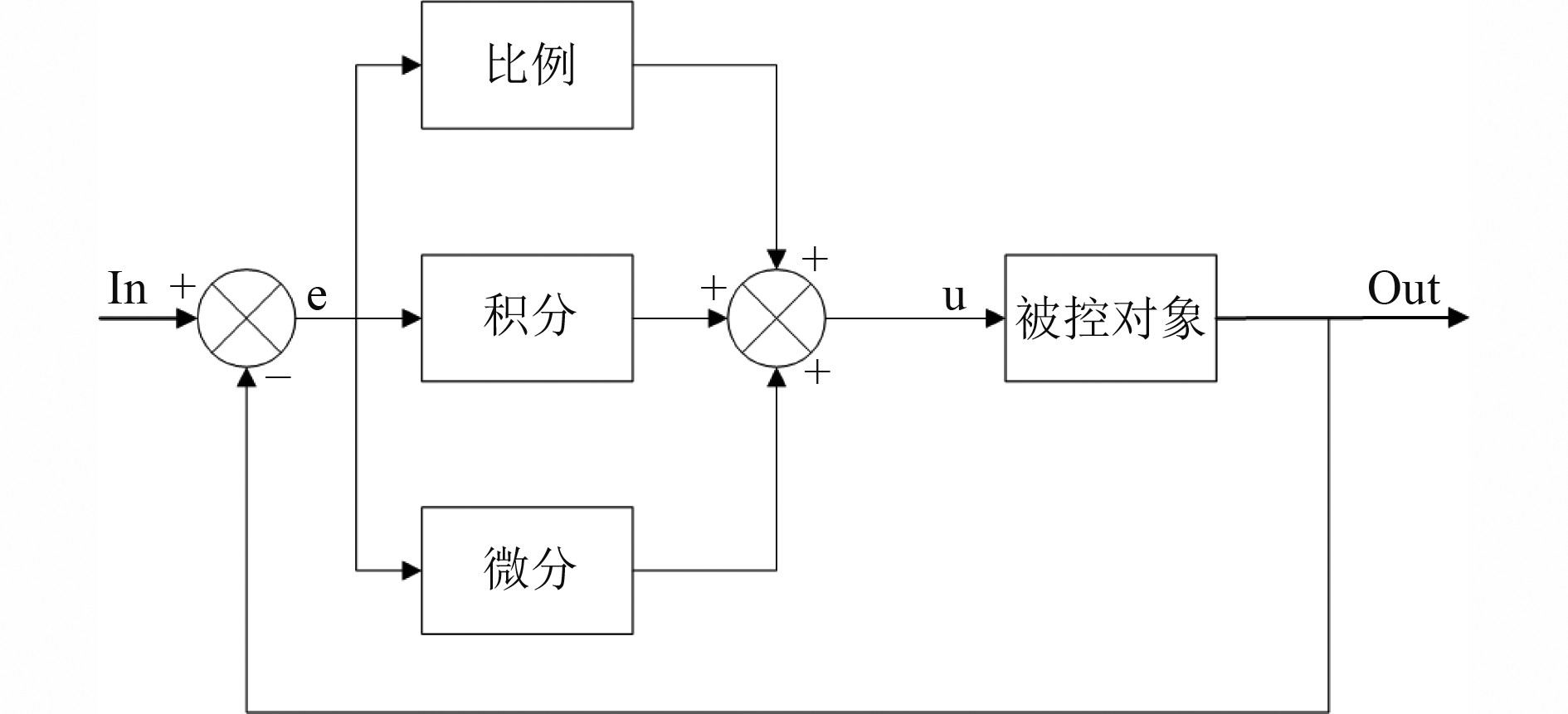
PID控制器的原理如图1所示，由比例、积分、微分3个部分构成。In为目标信号，Out为被控对象的输出，二者的差值e为偏差信号，u为控制器输出。被控对象的输入信号可表示为：

$ {u}\left({t}\right)={K}_{p}e\left(t\right)+{K}_{i}{\int }_{0}^{t}e\left(t\right){\rm{d}}t+{K}_{d}\frac{{\rm{d}}e\left(t\right)}{{\rm{d}}t}。$

(3)

式中，当参数 $ {K}_{i}=0 $ 时，图1所示结构为经典的PD控制。 $ {K}_{p} $ ， $ {K}_{i} $ ， $ {K}_{d} $ 等3个参数的调节有遗传算法^[10]、神经网络^[11]等智能化整定方法，由于遗传算法容易出现过早收敛，神经网络算法对样本有依赖性，采用改进的粒子群优化算法对PID控制器的3个参数进行调节，使AUV对深度具有良好的跟踪性。

3 IWEPSO算法 3.1 粒子群优化算法

粒子群优化算法（particle swarm optimization, PSO）是学者受到鸟类觅食的启发而设计出的一种寻优算法。鸟群觅食的时候会通过相互之间的信息传递来不断调整自己的飞行速度和方向，不断靠近食物。将粒子群和鸟群进行类比，得出以下迭代公式：

$ {v}_{i}^{k+1}=\omega {v}_{i}^{k}+{c}_{1}{r}_{1}\left(p{Best}_{i}^{k}-{p}_{i}^{k}\right)+{c}_{2}{r}_{2}\left(gBest-{p}_{i}^{k}\right)，$

(4)

$ {p}_{i}^{k+1}={p}_{i}^{k}+{v}_{i}^{k+1} 。$

(5)

式中： $ {r}_{1} $ 和 $ {r}_{2} $ 为[0,1]范围内的随机数， $ v $ 为粒子速度， $ p $ 为粒子位置， $ pBest $ 为单个粒子自迭代开始以来的最优位置， $ gBest $ 为所有粒子自迭代以来的最优位置。 $ {\omega v}_{i}^{k} $ 代表上一代的个体速度对本代个体速度的影响， $ {c}_{1}{r}_{1}\left(p{Best}_{i}^{k}-{p}_{i}^{k}\right) $ 的存在可以使单个粒子移动到比上一次更好的位置， $ {c}_{2}{r}_{2}\left(gBest-{p}_{i}^{k}\right) $ 的存在可以使所有粒子不断逼近目标。 $ {c}_{1} $ 和 $ {c}_{2} $ 均为加速常数，一般取0～4之间的常数，分别表示 $ \left(p{Best}_{i}^{k}-{p}_{i}^{k}\right) $ 和 $ {r}_{2} $ $ \left(gBest-{p}_{i}^{k}\right) $ 对粒子移动速度的影响。 $ \mathrm{\omega } $ 为非负的惯性因子， $ \mathrm{\omega } $ 取值大时粒子群的搜索范围较大， $ \mathrm{\omega } $ 取值小时粒子群的搜索范围较小。对 $ \mathrm{\omega } $ 的普遍处理方式为逐渐减小 $ \mathrm{\omega } $ 的值，但当惯性因子的数值减小得过快时，容易造成粒子群的早熟收敛，陷入局部最优解，因此常通过寻找适合的策略来动态调整惯性因子的值，使得粒子群算法达到满意的效果。

3.2 IWEPSO

传统的惯性权重线性递减PSO公式如下：

$ \mathrm{\omega }\left(k\right)={\omega }_{{\rm{max}}}-\left({\omega }_{{\rm{max}}}-{\omega }_{{\rm{min}}}\right)\cdot\frac{k}{{k}_{{\rm{max}}}}。$

(6)

式中： $ k $ 为迭代次数， $ {k}_{{\rm{max}}} $ 为最大迭代次数， $ {\omega }_{{\rm{max}}} $ 和 $ {\omega }_{{\rm{min}}} $ 分别为惯性权重上下限，常取0.9和0.4。如图2所示，惯性权重的变化象征着粒子从大范围搜索收敛到小范围搜索的过程。但是PSO的惯性权重减小的速率恒定不变，为了加快粒子群在迭代中后期的收敛速度，张继荣等^[7]提出的IWCPSO，惯性权重变化规律为：

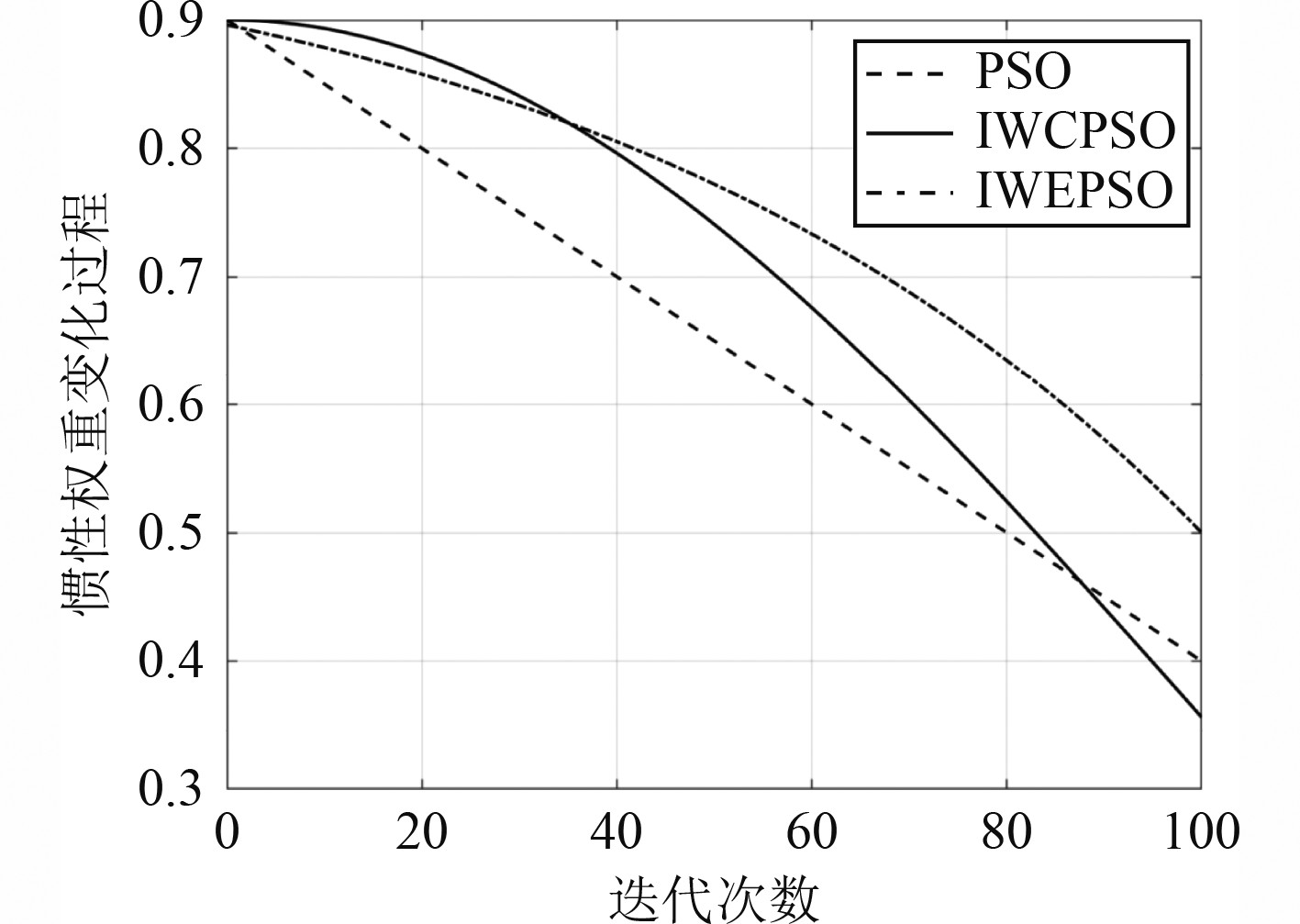
$ \mathrm{\omega }\left(k\right)=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\cdot{\omega }_{{\rm{min}}}\cdot\left(1-\mathrm{cos}h\right)+{\omega }_{{\rm{max}}}\cdot\mathrm{cos}h。$

(7)

式中： $ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d} $ 为0～1之间的随机数， $ {\omega }_{{\rm{min}}}=0.4 $ ， $ {\omega }_{{\rm{max}}}= $ $ 0.9 $ ， $ h=\text{π} k/2{k}_{{\rm{max}}} $ 。如图2所示，IWCPSO在迭代的初期，惯性权重下降得较慢，后期下降较快，可以看出，由于随机数 $ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d} $ 的存在，会使得惯性权重小于0.4，这样虽然加快了收敛，但是在实际的应用中，后期的加速处理可能导致粒子群的早熟。在PSO公式和IWCPSO公式的基础上，考虑到欠驱动AUV的控制器要求，为避免PSO早熟，设计了一种惯性权重指数调整的粒子群优化算法（inertial weight exponential particle swarm optimization，IWEPSO）如下式：

$ \mathrm{\omega }\left(k\right)=\left({\omega }_{{\rm{min}}}-{\omega }_{{\rm{max}}}\right){\mathrm{e}}^{h-\frac{\text{π} }{2}}+1。$

(8)

式中： $ {\omega }_{{\rm{min}}}=0.4 $ ， $ {\omega }_{{\rm{max}}}=0.9 $ ， $ h=\text{π} k/2{k}_{{\rm{max}}} $ 。由图2可知，该算法的惯性权重缓慢减小，可以更好地避免粒子群陷入局部最优解。

3.3 IWEPSO应用于欠驱动AUV的PID控制器参数整定

具体步骤如下：

步骤1　选取性能指标：为了使欠驱动AUV的深度控制快速收敛、减小超调量，选取

$ ITAE={\int }_{0}^{\infty }t\left|e\left(t\right)\right|{\rm{d}}t，$

(9)

作为适应度函数，对于本文的非线性系统，性能指标为：

$ ITAE=\sum _{i=0}^{k}i\left|e\left(i\right)\right| 。$

(10)

式中： $ k $ 为当前迭代次数， $ e\left(k\right) $ 为AUV的目标深度与当前实际深度的差。

步骤2　IWEPSO参数初始化：规定粒子的维数为3，设置粒子数量、速度边界和位置边界、 $ {k}_{{\rm{max}}} $ 和适应度函数的最小值，并在规定的范围内随机初始化粒子的速度和位置。

步骤3　粒子群的3个维度分别对应 $ {K}_{p} $ ， $ {K}_{i} $ ， $ {K}_{d} $ 等3个参数，开辟工作空间用来保存 $ gBest $ 和 $ pBest $ 的值，便于后续比较。

步骤4　根据IWEPSO对惯性权重进行调整，利用迭代公式（4）和公式（5）得到新一代粒子群。每一组粒子群的位置数值代表着每一组PID控制器的3个参数值，将每次迭代得到的控制器参数代入PID控制器，对欠驱动AUV进行控制。

步骤5　当适应度函数小于步骤1所设置的值或迭代次数达到步骤1所设置的最大值，进入步骤6，否则进入步骤4。

步骤6　迭代结束，得到全局最优值。

4 仿真实验及结果分析 4.1 仿真实验

图3为在研欠驱动AUV的外观图，AUV长2.32 m，最大横截面直径0.24 m。AUV上配备天线，便于在水面上运行时与控制台进行数据收发。AUV尾部的螺旋桨提供推力，螺旋桨前方的十字舵控制AUV的姿态。

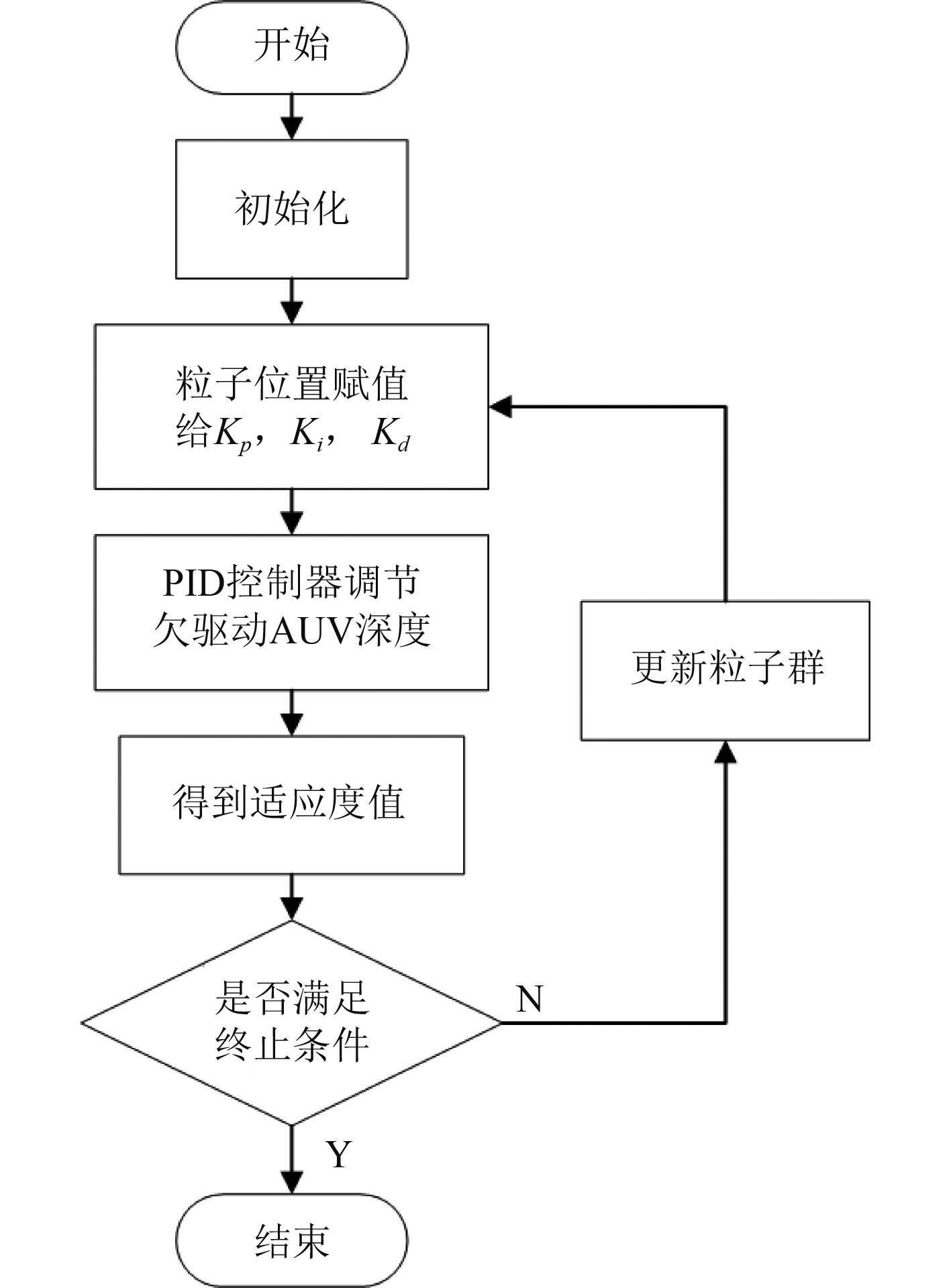
以图3所示AUV为原型，基于Matlab 2019b进行仿真，算法的流程如图4所示。式（2）所涉及的水动力参数^[9]为：

$\begin{split} & m=2\;535\;{\rm{kg}} , {X}_{\dot{u}}=-142 \;{\rm{kg}} ,{Y}_{\dot{v}}=-1\;700\;{\rm{kg}} ,\\ &{Z}_{\dot{w}}=-4\;600\;{\rm{kg}} , {I}_{y}=1\;700\;{\rm{kg}}\cdot {{\rm{m}}}^{2} , \\ & {I}_{z}=2\;000\;{\rm{kg}}\cdot {{\rm{m}}}^{2} , {M}_{\dot{q}}=-1\;700\;{\rm{kg}}\cdot {{\rm{m}}}^{2}/{\rm{rad}} ,\\ & {N}_{\dot{r}}=-1\;350\;{\rm{kg}}\cdot {{\rm{m}}}^{2}/{\rm{rad}} ,\\ & {X}_{u\left|u\right|}=-35\;{\rm{kg}}/{\rm{m}},{Y}_{v\left|v\right|}=-667\;{\rm{kg}}/{\rm{m}} ,\\ & {Z}_{w\left|w\right|}=-2\;000\;{\rm{kg}}/{\rm{m}} , {Y}_{v}=-346\;{\rm{kg}}/{\rm{m}} , \\ & {Z}_{w}=-1\;000\;{\rm{kg}}/{\rm{m}} , {M}_{q}=-900\;{\rm{kg}} \cdot {{\rm{m}}}^{2}/{{\rm{rad}}}^{2} , \\ &{N}_{r}=-300\;{\rm{kg}}\cdot {{\rm{m}}}^{2}/{{\rm{rad}}}^{2} , \\ &{M}_{q\left|q\right|}=-1\;100\;{\rm{kg}}\cdot {{\rm{m}}}^{2}/{{\rm{rad}}}^{2} , {N}_{r\left|r\right|}=-350\;{\rm{kg}} \cdot {{\rm{m}}}^{2}/{{\rm{rad}}}^{2} 。\end{split}$

舵效系数 ${M}_{{\delta }_{s}}=900\;{\rm{kg}}/{\rm{rad}}$ ， ${N}_{{\delta }_{r}}=850\;{\rm{kg}}/{\rm{rad}}$ ，由于本文研究的是欠驱动AUV的深度控制，所以在广义力 $ \mathrm{\tau }=[{F}_{x},\mathrm{0,0},0,{\delta }_{s},{\delta }_{r}] $ 中，将尾部主推力设置为恒定值 $ {F}_{x}=200 $ ，控制AUV绕载体坐标系z轴转动的力 $ {\delta }_{r}= $ $ 0 $ ，控制AUV绕载体坐标系转动的力为：

$ {\delta }_{s}={K}_{p}e\left(k\right)+{K}_{i}\sum _{i=0}^{k}e\left(i\right)+{K}_{d}\cdot \left[e\left(k\right)-e\left(k-1\right)\right]。$

(11)

式中的 $ e\left(k\right) $ 等于期望深度与AUV的实际深度 $ {Z}_{e} $ 之差，本文设AUV的期望深度为5 m。至此，以 $ \mathit{v}=[u,v, $ $ w,q,r]^{{\rm{T}}} $ 为状态变量的非线性微分方程（2）可以通过4阶龙格-库塔法^[12]进行解算。

设置学习因子 $ {c}_{1}={c}_{2}=2 $ ，粒子个数为100，迭代次数为50，粒子的最大速度为1.5，粒子位置的取值范围为0～300，取 ${\omega }_{{\rm{min}}}=0.4$ ， ${\omega }_{{\rm{max}}}=0.9$ 。运行上述欠驱动AUV模型后，计算出适应度值，即 $ ITAE $ 值，如果 $ ITAE $ 值满足要求，则结束流程，如果不满足要求，则对粒子群进行迭代更新。

4.2 实验结果分析

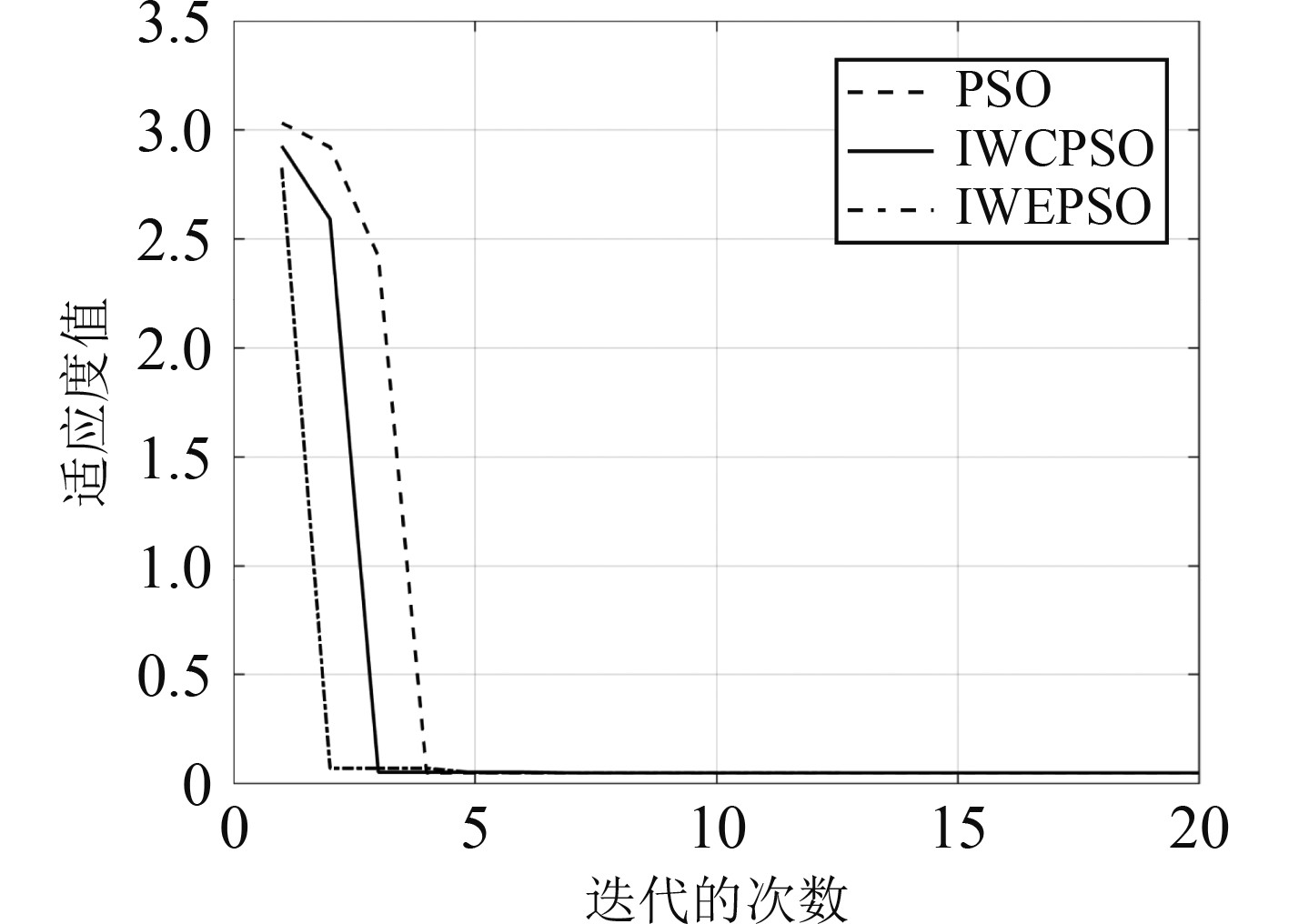
运行欠驱动AUV模型，模型的PID控制器分别用PSO，IWCPSO和IWEPSO进行参数整定，不同方法下，模型的 $ ITAE $ 值随迭代次数的变化如图5所示。图中截取了前20次的迭代数据，PSO，IWCPSO，IWEPSO分别在迭代次数为4，3，2时收敛。通过对IWEPSO的纵向比较，证明了该算法的收敛性。

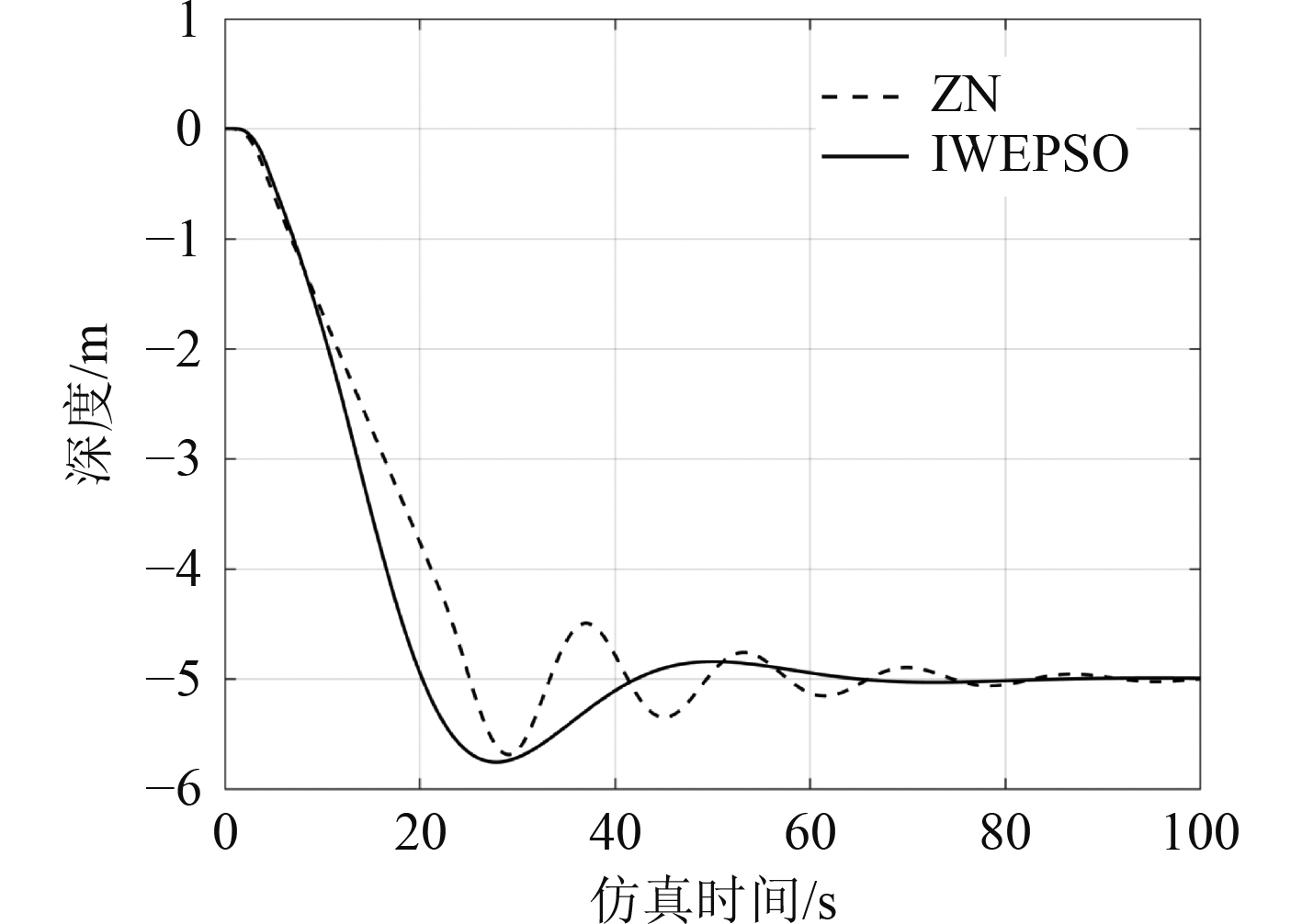
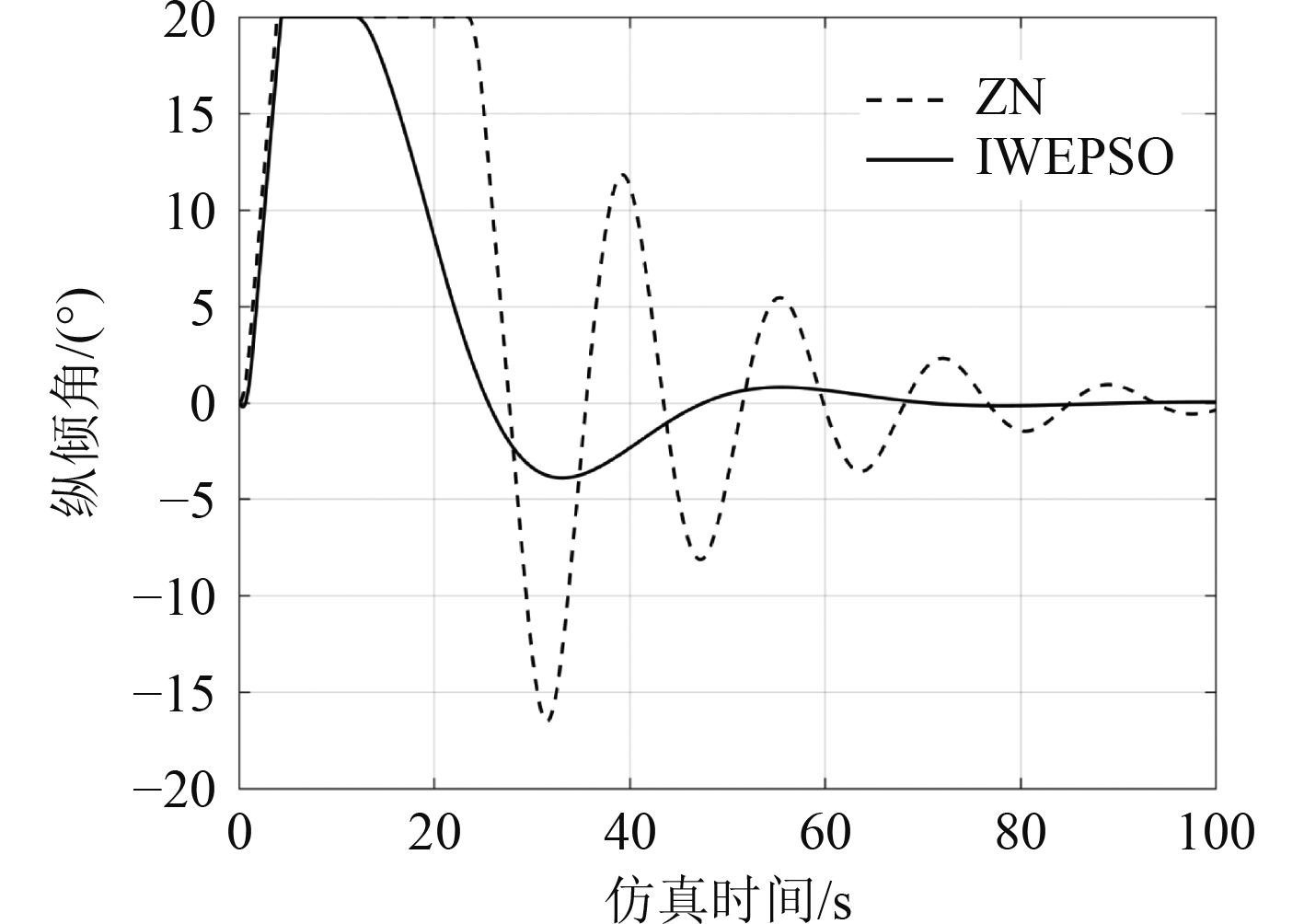
ZN法整定的PID控制器收敛性极差，因此分别用ZN法整定后的PD控制器和IWEPSO整定后的PID控制器对欠驱动AUV进行控制，并进行横向对比。AUV的深度变化如图6所示。可知，IWEPSO整定后的PID控制器可以使AUV更快达到稳定状态，且稳定过程相对平滑。设置AUV在体坐标系下绕y轴旋转的最大角度为20°，图7为AUV的纵倾角变化曲线。可知，在仿真初期，为了快速到达目标深度，基于ZN法和IWEPSO的AUV保持较大的纵倾角，当接近目标深度时，IWEPSO比ZN法相比，响应更加迅速，纵倾角减小更加及时。在仿真中后期，ZN法整定的PD控制器使AUV频繁改变纵倾角的方向，IWEPSO整定的PID控制器使AUV平滑运行，因此，IWEPSO在工程中可很大程度减小舵机损耗。

ZN法整定的2种控制器和IWEPSO整定的PID控制器的整定及仿真结果如表1所示。当使用ZN法进行参数整定时，需要事先选择控制器的形式，一旦选择错误，就可能导致系统发散，而IWEPSO可以直接用于PID整定，无需考虑控制器形式的选择。与ZN法整定的PD控制器相比，IWEPSO整定的PID控制器可以使AUV的上升时间和调节时间更短，极大程度加速了系统响应。

5 结　语

本文对欠驱动自主水下航行器进行定深控制，引入指数函数对粒子群优化算法的惯性权重进行动态调整，利用改进的粒子群优化算法对PID控制器进行了参数整定。与PSO和IWCPSO进行纵向对比，证明了改进的粒子群优化算法的收敛性；与ZN整定法进行横向对比，证明了改进的粒子群优化算法的快速性和平稳性。后续将开展AUV的湖上和海上试验，并对算法做进一步修正。