模糊控制理论沿用了“模糊数学”概念的全部基础思想与控制方法,可以在准确判别指标参量系数值真实性的同时,控制误差干扰项量差的数值偏离程度,不但可以获得多个真实数值解,也可以按照模糊算法将所有求取数值排列起来,从而大大节省计算数据消耗的时间。对于复杂的数据集合来说,常规控制算法所需经历的数据处理步骤过于繁琐,且在大量的数据运算过程中,极易因小的疏忽,而导致最终求取结果失去真实性[1-2]。模糊控制理论则有效解决了上述问题,在求解过程中,只需计算数值参量所属的大致区间,节省了大量的数据运算步骤,虽然计算数值不够精确,但由于数值解的排列顺序完全符合真实性要求,所以并不会对计算机指令的执行结果造成影响。
对于船舶主机而言,在运行环境中,其行进方向会受水动力影响而发生改变,此时船舶很有可能偏离其预设航线,并最终进入错误的航行轨迹之中[3]。而在实际应用过程中,若出现船舶偏航的情况不但会影响主机元件对于运动路线的控制能力,也会使得中心基站无法对船舶前进行为进行准确判断。为解决上述问题,传统的变论域模糊控制技术通过定位阶段性航行节点的方式,来确定船舶的实时行进位置,再联合操纵控制主机,对整条航行轨迹的可行性进行判别[4]。然而此方法并不能使船舶行进水动力与预设动力数值曲线较好贴合,容易失去对于船舶运动状态的主动控制权。为避免上述情况的发生,以模糊控制理论为基础,设计一种新型的船舶操作运动模型,并通过比对实验的方式,突出该模型的实际应用价值。
1 基于模糊控制理论的船舶操纵运动模型 1.1 模糊滤波监测器模糊滤波监测器是能够充分展现模糊控制理论的信号闭环,一般来说,模糊滤波监测器元件中至少有2类信号保持同步传输状态,且2类信号参量之间存在明显的传输干扰关系[5]。在船舶操纵运动模型中,模糊滤波监测器同时定义了航向信号与航速信号,前者决定了船舶主机的实际行进方向,而后者则可以对航行过程中的前进速度进行调试。
| $ \theta = \frac{[{{f_1}^2\left( {{\phi _1}} \right) - {f_2}^2\left( {{\phi _2}} \right)}]{{\sqrt[\uproot{5}{{ \rho}} ]{{{j_1}^2 - {j_2}^2}}}}}{{\lambda \beta \left| {\Delta E} \right|} {{\left| {K' - \bar K} \right|}^2}}。$ | (1) |
式中:
航向信号、航速信号间的数值配比关系,是构建模糊滤波监测器闭环模型的关键条件。
图1展示了船舶模糊滤波监测器结构的实际连接原理。可知,模糊控制算法同时约束船舶主电机回路、AAI监测主机、船舶运动信号与船舶运动主机。其中,船舶主电机回路掌管船舶设备在行进航迹中的运动行为,且随着船舶运动航迹的延长,主电机元件的执行能力也在不断增强[2,6]。电动机设备决定了AAI操纵芯片对于船舶运动方向的控制能力,由于滤波执行设备元件的存在,上述2类设备结构不具备独立运动的能力,且在模糊控制算法的影响下,船舶操纵主机的连接形式受到滤波回路的直接影响[7]。船舶运动主机直接决定了船舶在行进路径中的运动能力,若将模糊滤波监测器看作一个完整的船舶运动行为控制设备,则可认为主机元件中数据信息的输出能力越强,船舶设备所表现出来的行进能力也就越强。船舶运动信号是一类传输能力较强的数据信息参量,在模糊控制算法的作用下,这些数据信息可以在模糊滤波监测器元件中自由传输。
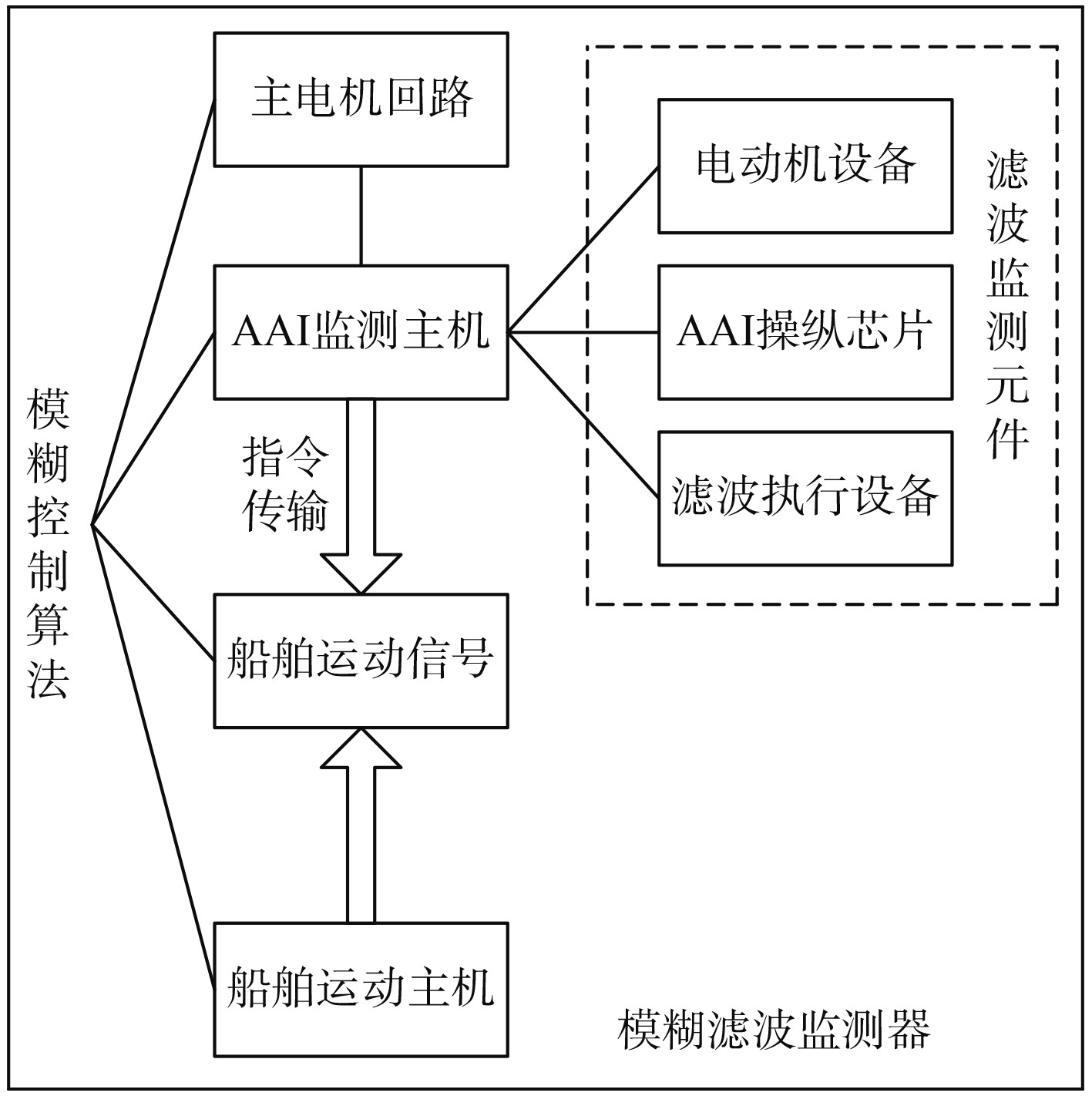
|
图 1 模糊滤波监测器的结构示意图 Fig. 1 Structure diagram of fuzzy filter monitor |
航向控制表达式也称船舶操纵运动方向的控制表达式,在建立模型条件时,应在模糊控制理论的作用下,计算相关航迹向量的数值水平[8-9]。若将模糊滤波监测器看作一个完整的信号闭环结构,则可认为随着船舶运动方向的改变,与之相关的航向控制表达式定义结果也会发生改变,但后者的变化程度始终受到前者的影响。设
在上述物理量的支持下,联立式(1),可将基于模糊控制理论的船舶航向控制表达式定义为:
| $ F = \frac{{{\left| {{s_1} + {s_2} + \cdots + {s_z}} \right|}^2}{{\theta }{{\left| {\bar D} \right|}^2}\displaystyle\sum\limits_{s = 1}^n {\sqrt {{l_n}^2 - {l_s}^2} } }} {{\chi \hat q \displaystyle\sum\limits_{\varepsilon = 1,\sigma = 1\hfill} {{{\dot y}^2} - \left( {{y_\varepsilon } + {y_\sigma }} \right)} {{}}}}。$ | (2) |
式中:χ表示模糊滤波监测器中的传输信号闭环特征;
在模糊控制理论算法的作用下,航向控制表达式可以直接约束船舶桨力操纵量与舵力操纵量的数值计算结果。
1.3 桨力操纵量桨力操纵量是船舶操纵运动模型中的关键物理指标。在模糊控制理论原则的作用下,桨力操纵量指标的计算表达式受到船桨推力减额系数、进速系数、桨推力3项物理参量的直接影响。船桨推力减额系数可表示为ξ,在船舶操纵运动模型中 ,该项物理参量的最小取值结果只能等于自然数“1”。进速系数可表示为
| $ {h_1} = \frac{F}{{\sqrt {\dfrac{{\dot x}}{\xi } + \frac{1}{{{{\left( {{\raise0.7ex\hbox{$k$} \mathord{\left/ {\vphantom {k B}}\right.} \lower0.7ex\hbox{$B$}}} \right)}^2}}}} }} \cdot {\left| {\dfrac{{{\gamma _1} \cdot {\tau _1}}}{{{b_1} \cdot {{\vec a}_1}}}} \right|^2} 。$ | (3) |
式中:
在已知模糊控制理论作用能力的情况下,航向控制表达式可以直接影响桨力操纵量定义表达式的计算值结果。
1.4 舵力操纵量舵力操纵量决定了船舶主机对于船体操纵运动行为的控制能力。在已知桨力操纵量表达式的前提下,模糊控制理论可以直接影响舵力操纵量指标的数值计算结果。
| $ {h_2} = \frac{{{h_1}^2 - \beta \dfrac{{\mu \left( {{{\tilde g}^2} - {{\bar A}^2}} \right)}}{{\varpi \sqrt {{{\left| {{c_v} - {c_m}} \right|}^{v - m}}} }}}}{{{{\left| {\dfrac{{{\gamma _2} \cdot {\tau _2}}}{{{b_2} \cdot {{\vec a}_2}}}} \right|}^2}}} 。$ | (4) |
式中:β表示基于模糊控制理论的船舶行进运动系数;
在图2所示的水域环境中,人工设置2条直线作为船舶运动的起始线与终止线。将实验组、对照组船舶置于航迹路线中,令二者运动速率保持一致。具体实验设计流程如下:
1)利用基于模糊控制理论的船舶操纵运动模型控制实验组船舶;
2)利用变论域模糊控制技术控制对照组船舶;
3)分别统计实验组、对照组船舶的行进水动力数值;
4)将实验组、对照组水动力数值与预设动力数值进行对比。
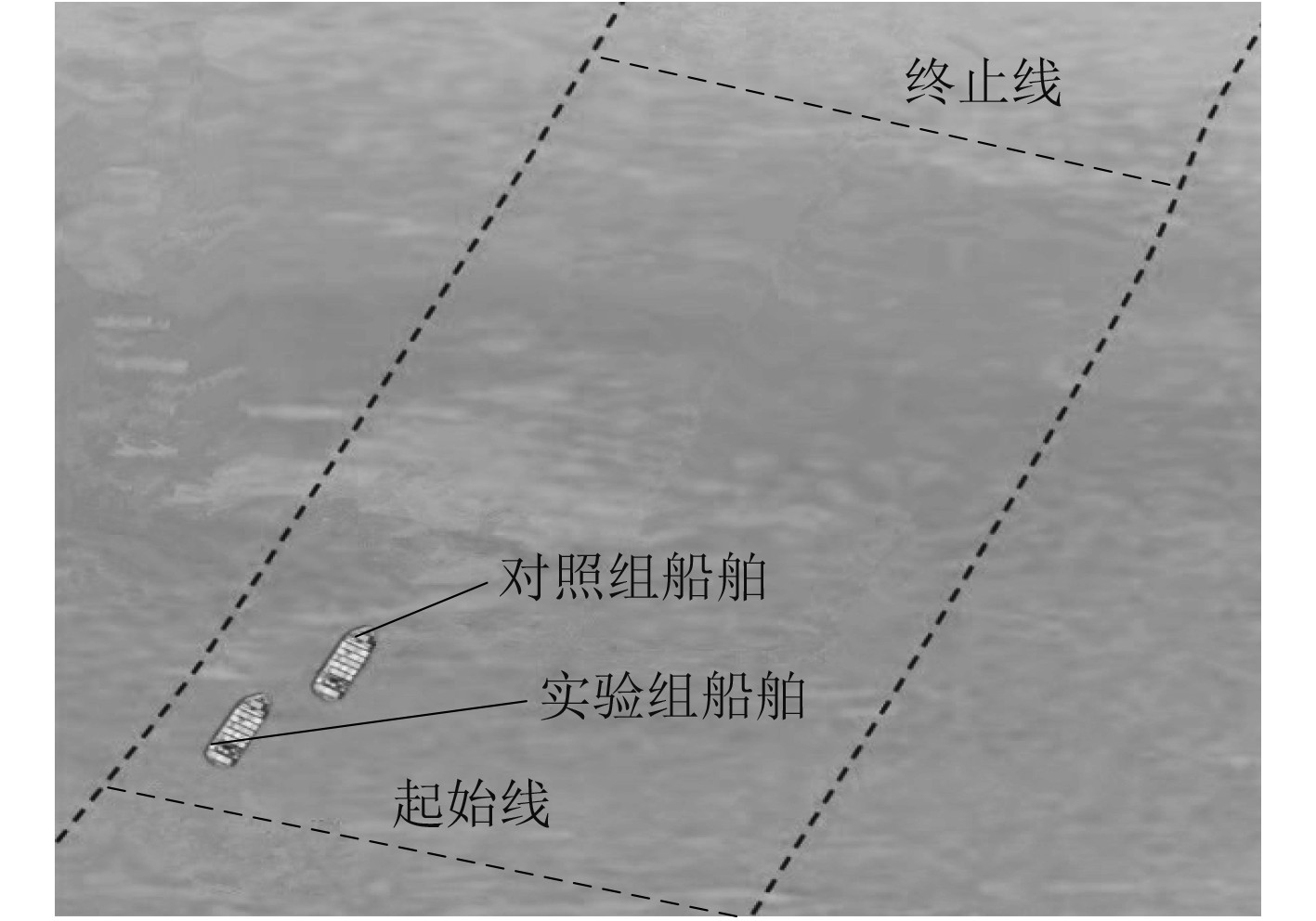
|
图 2 船舶运动航迹线路 Fig. 2 Ship track |
受到水体流动特性的影响,起始线与终止线并不一定是一条竖直或水平的直线,而是一条可以随着水波纹变化形式不断变化的曲线,这样不但可以避免水体运动行为对船舶路径造成的影响,还可以使得船舶行进路径范围得到有效扩充。
为获得准确的实验结果,按照表1所示指标数值,完成对实验组、对照组主机元件的配置。
|
|
表 1 实验参数配置 Tab.1 Experimental parameter configuration |
为保证实验结果的真实性,实验组、对照组实验参数始终保持一致。
船舶行进水动力能够反映运动船舶在行进过程中的运动受控能力。一般来说,船舶行进水动力数值与预设水动力数值的贴合性越强,就表示运动船舶在行进过程中的运动受控能力越强;反之,若船舶行进水动力数值与预设水动力数值的贴合程度较差,则表示运动船舶在行进过程中的运动受控能力也相对较弱。船舶行进水动力由横向数值和纵向数值共同组成。其中,横向行进水动力表示了船舶主机对于横向水流的控制能力,纵向行进水动力表示了船舶主机对于纵向水流的控制能力。
图3反映了船舶横向行进水动力数值与预设水动力数值间的贴合情况。分析可知,随着行进距离的延长,预设水动力数值始终保持来回波动的变化状态,但明显两端数值较小、中间区段数值较大。实验组水动力数值的变化趋势基本与预设水动力数值保持一致,二者极大值均为6.53×105 N。对照组水动力数值虽然也呈现出来回波动的变化状态,但并不能与预设水动力数值贴合,整个实验过程中的水动力极大值达到了7.78×105 N,高于实验组水动力数值。
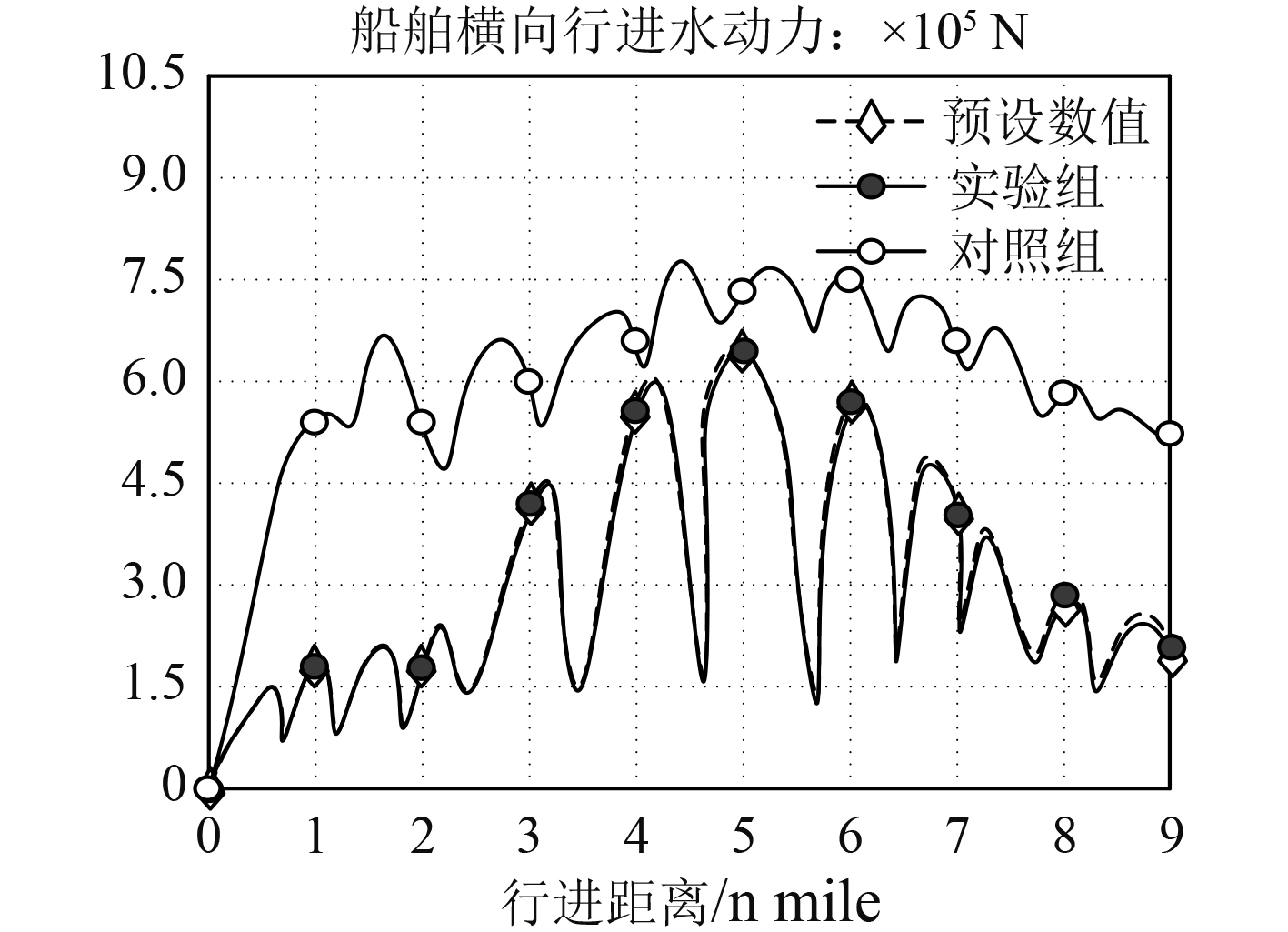
|
图 3 船舶横向行进水动力数值 Fig. 3 Dynamic values of ship transverse running water |
图4反映了船舶纵向行进水动力数值与预设水动力数值间的贴合情况。分析可知,在整个实验过程中,预设水动力数值基本保持不断上升的变化状态,而当行进距离等于4.0 nmile时,预设水动力数值出现了明显下降的变化状态。实验组水动力数值的变化趋势基本与预设水动力数值保持一致,二者极大值均为7.50×105 N。对照组水动力数值也基本保持不断上升的变化趋势,但当行进距离等于7.0 nmile时,对照组水动力数值出现了明显下降的变化状态,整个实验过程中,其最大值达到了9.23×105 N,高于实验组水动力数值。
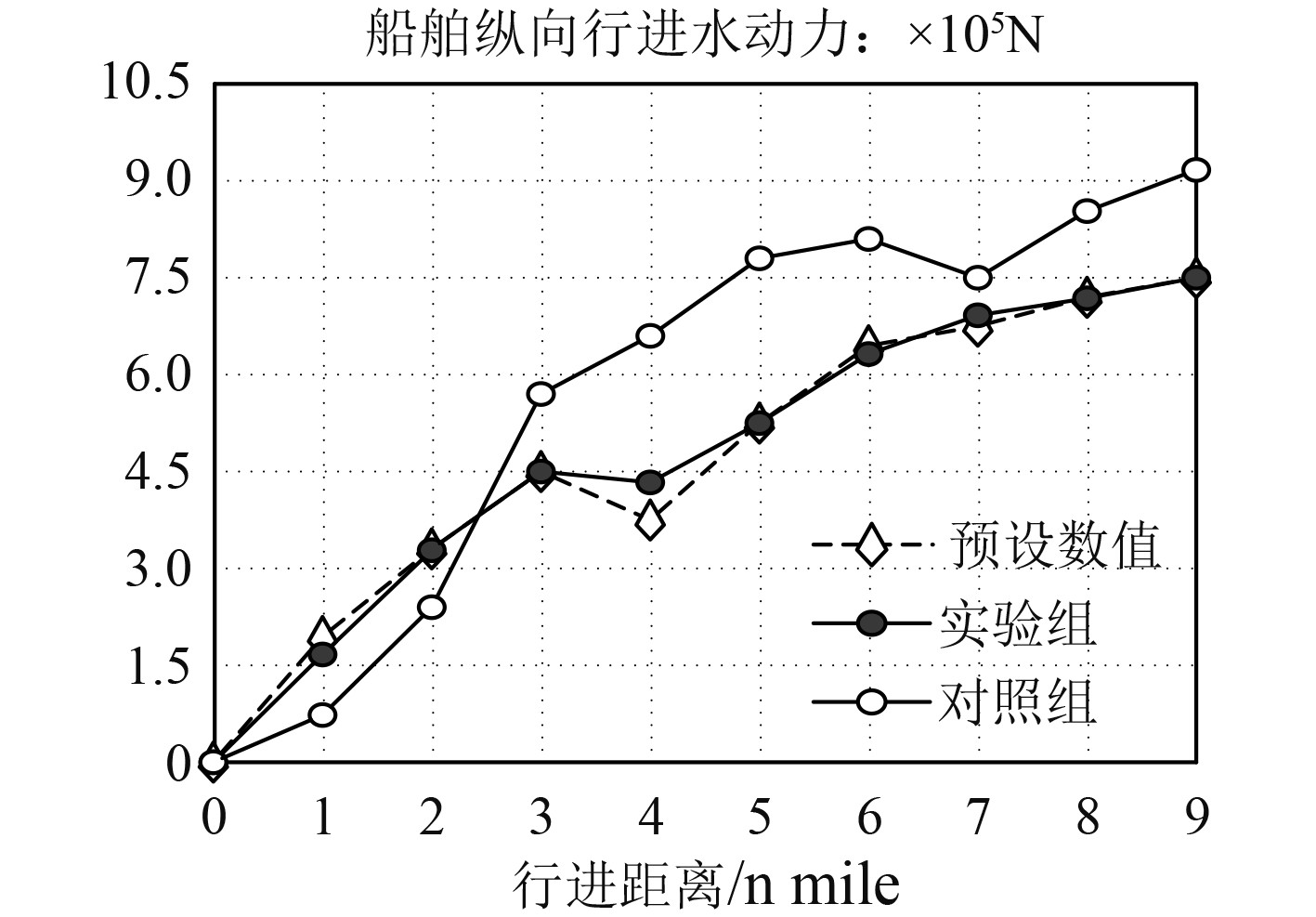
|
图 4 船舶纵向行进水动力数值 Fig. 4 Numerical value of longitudinal inflow force of ship |
综上可知,本次实验结论如下:
1)在变论域模糊控制技术作用下,船舶横向行进水动力数值、纵向行进水动力数值均不能与预设水动力数值保持较好的贴合状态;
2)在模糊控制理论的作用下,船舶横向行进水动力数值、纵向行进水动力数值都可以与预设水动力数值保持高度贴合的存在状态;
3)基于模糊控制理论的船舶操纵运动模型能够促使船舶行进水动力数值与预设动力数值曲线更好贴合,符合稳定操纵船舶运动行为的实际应用需求。
3 结 语在模糊控制理论算法的支持下,船舶操纵运动模型以模糊滤波监测器闭环作为切入点,在建立完整航向控制表达式的同时,分别对桨力操纵量、舵力操纵量进行采集。与变论域模糊控制技术相比,模糊控制理论算法的应用,解决了船舶行进水动力数值与预设水动力数值曲线间贴合状态较差的问题,能够帮助船舶主机稳定操作船体运动行为,在实际应用方面具有较强的可行性价值。
| [1] |
张叶, 任鸿翔, 王德龙. 基于KNN算法的船舶操纵智能评估系统[J]. 上海海事大学学报, 2021, 42(4): 33-38. |
| [2] |
孙寒冰, 肖佳峰, 王伟, 等. 船舶操纵水动力导数的数值求解及敏感度分析[J]. 中国舰船研究, 2022, 17(1): 60-70. |
| [3] |
欧阳承达, 张军, 赵红梅. 模糊控制系统模型在轴承故障诊断中的应用[J]. 工程技术研究, 2020, 66(10): 131-132. DOI:10.3969/j.issn.1671-3818.2020.10.059 |
| [4] |
黄斌, 吕帮俊, 彭利坤, 等. 变论域模糊控制在X舵抗干扰操纵中的应用[J]. 华中科技大学学报(自然科学版), 2020, 48(7): 40-46. |
| [5] |
梅斌, 孙立成, 史国友, 等. 基于单参数自调节RM-GO-LSVR的船舶操纵灰箱辨识建模[J]. 交通运输工程学报, 2020, 20(2): 88-99. |
| [6] |
王立鹏, 张智, 马山, 等. 考虑船舶操纵性约束的改进遗传算法航线规划[J]. 哈尔滨工程大学学报, 2021, 42(7): 1056-1062. |
| [7] |
王川隘, 童思陈, 蒋聘凤, 等. 风流效应下船舶操纵运动数值模拟[J]. 大连海事大学学报, 2020, 46(3): 50-59. |
| [8] |
欧阳子路, 王鸿东, 王检耀, 等. 基于智能控制的船舶水动力导数敏感性分析方法[J]. 中国舰船研究, 2021, 16(4): 116-124. |
| [9] |
张国庆, 姚明启, 杨婷婷, 等. 考虑事件触发输入的船舶自适应动力定位控制[J]. 控制理论与应用, 2021, 38(10): 1597-1606. DOI:10.7641/CTA.2021.00416 |
 2022, Vol. 44
2022, Vol. 44
