0 引　言

舰船建造是一项复杂工程，在研制中需要利用运动轨迹跟踪平台真实再现舰船在航行中出现的摇摆姿态，为建造和驾驶员航海训练提供平台。在舰船运动轨迹跟踪模拟中，设计六自由度模拟摇摆平台是关键点之一。本文提出优化后的基于遗传算法的运行轨迹跟踪模型，搭建起舰船模拟摇摆平台^[1-3]。

1 六自由度舰船运动模拟平台 1.1 运动模拟平台的技术要求

六自由度舰船模拟运动平台的最大负载重量为1 000 kg，可以分为如下3种运动方式：1）单自由度摇摆运动；2）两自由度复合摇摆运动；3）三自由度复合摇摆运动。3种运动方式要求的幅度与周期指标如下：

单自由度摇摆运动中的横摇幅度范围为−45°～+45°，周期＜8 s；纵摇幅度范围为−10°～+10°，周期＜4 s；升沉幅度范围为−270～+270 mm，周期＜4 s。

两自由度复合摇摆运动中的横摇幅度范围为−16°～+16°，周期＜8 s，纵摇幅度范围为−8°～+8°，周期＜4 s^[4-6]。

三自由度复合摇摆运动中的横摇幅度范围为−17°～+17°，周期＜8 s，纵摇幅度范围为−7°～+7°，周期＜4 s。

1.2 运动模拟平台选型

选用Stewart平台建设六自由度运动平台，共设置18个运动部位，与上下平台连接的自由度为3，局部自由度为6，具体结构如图1所示。

2 六自由度舰船运动轨迹跟踪算法 2.1 算法的关键参数

选用的模拟器运动机构由平台、底座、6个液压缸、铰链等部分组成。在该模拟器中，对结构起着决定性作用的参数包括上铰圆和下铰圆半径r和R；上铰和下铰的短边长度s和S；上铰圆与下铰圆平面距离h。上述参数的选取，对模拟器的运动空间、液压缸的受力、速度以及加速度的大小具有直接影响。依据以往的经验，s和S的取值不宜过大，与支座的结构有关。重点研究的参数包括r，R以及h，这3个参数的取值对液压缸的行程及受力具有一定程度的影响^[7-9]。

以六自由度的舰船运动模拟器设计指标作为主要依据，对用于计算的运动方式加以确定。在设计的起始阶段，最大线速度、位移和加速度等指标均为已知。以上述指标作为依据，能够确定出平台的运动方式。结合实际，在模拟运动仿真的同时展开计算。当运动方式确定之后，通过结构参数的选定，便可计算出液压缸行程及其最大的受力情况，具体如下：

$ \begin{gathered} Stroke = \max (st{r_{ji}}) ，i = 1,2 \cdots,6;j = 1,2\cdots,6 。\end{gathered} $

$ {F_{\max }} = \max (r,R,h)\cdot {F_{ji}} 。$

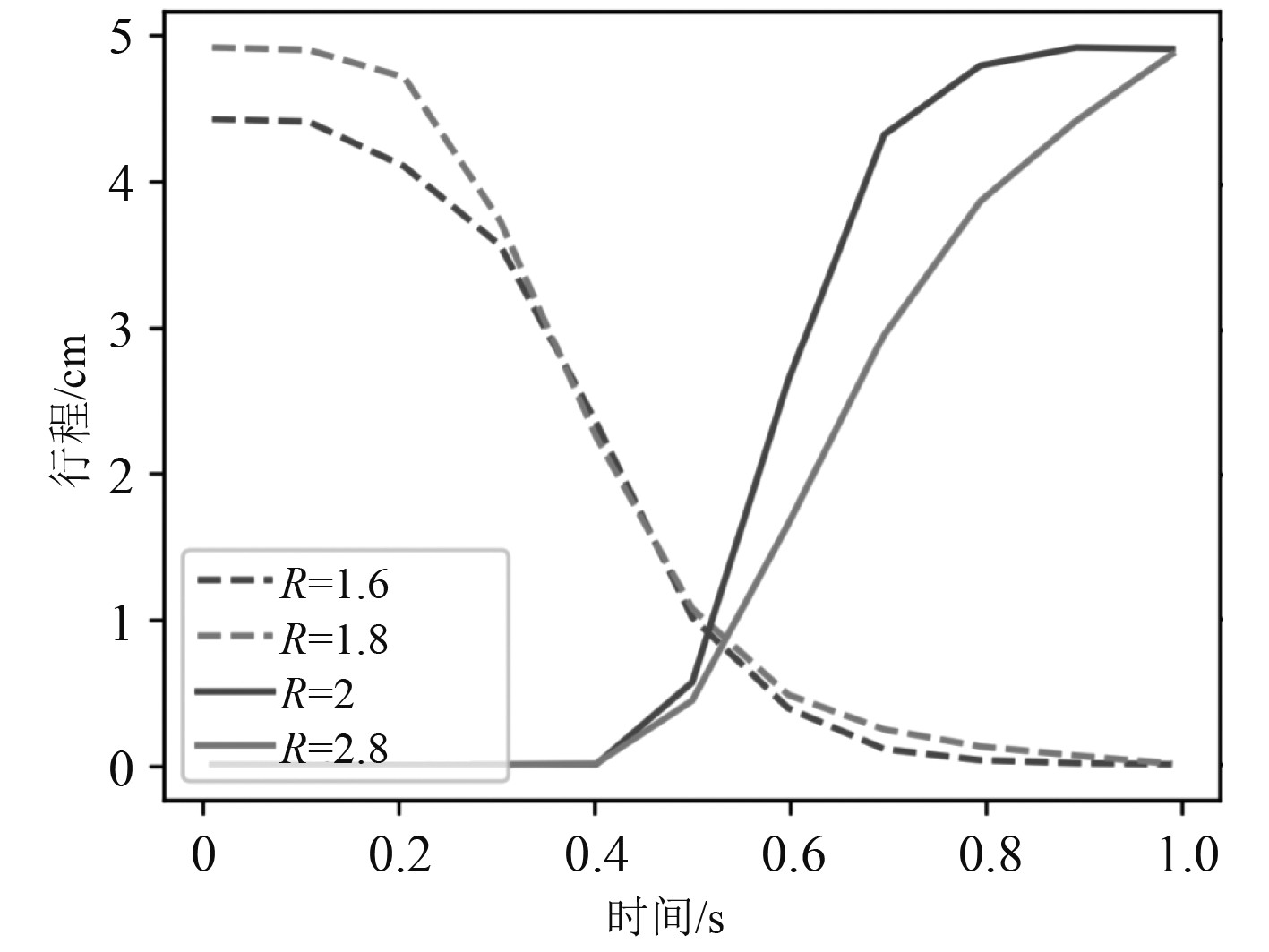
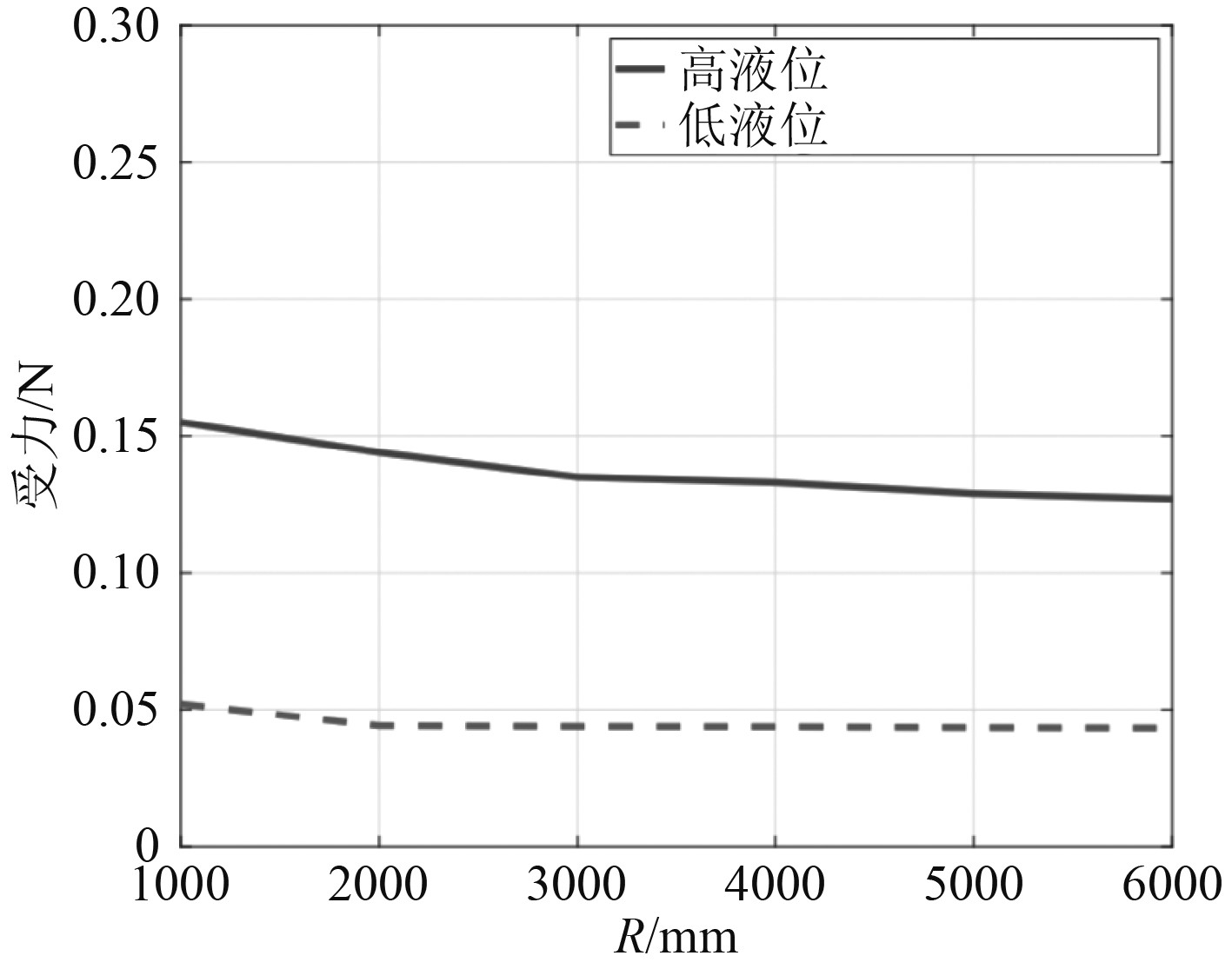
式中：Stroke为液压缸的行程，m；F_max为液压缸的最大受力，N；i为第i个液压缸；j为第j种参考运动方式；str_ji为第i个液压缸作第j种参考运动时的行程；F_ji与str_ji同理。利用上述计算公式，可以对模拟器中的主要参数r，R和h在不同取值下的行程与受力情况加以确定，进而分析其变化规律。r的取值范围为1.2～2.0 m，R的取值范围为1.6～2.8 m，h保持不变时，不同R值液压缸的行程和受力情况分别如图2和图3所示。

通过对图2进行分析后发现，在其他参数保持不变的前提下，液压缸的行程会随R值变化。然而，在模拟器的具体应用中，R的取值不宜过小，否则会导致平台的使用面积不足，这样一来在运动的过程中，很容易出现失稳或是倾覆的现象。为避免该情况的发生，R的取值必须适当。在R保持不变的情况下，将R增大后，液压缸的行程减小，速度相对比较缓慢，基于此，在具体设计中，可以通过改变R的取值来达到调整液压缸行程的目的。对图3进行分析后发现，在其他参数保持不变的前提下，单纯增大R，液压缸的受力会先减小后增大，减小的过程中，会出现一个极小值，之所以出现这样的情况，是因为要想实现平台高速的加速度，就需要液压缸的输出功率足够大。而当R增大后，液压缸的输出功率减小。R较大时，液压缸的受力随之减小；R较小时，液压缸的受力并未出现太大的变化，仅略微减小。所以从受力的层面看，曲面低谷区域对应的参数，均可作为模拟器的参数。

当r的取值保持不变时，液压缸的行程与受力情况分别如图4和图5所示。

通过对图4的分析发现，h减小后，液压缸行程随之减小，行程减小的速度与增大R时存在类似的情况。在分析后发现，h对液压缸受力的影响与r相类似，当其他参数保持不变，增大h，液压缸的推力会在Z坐标的方向上增大，而X和Y坐标的方向会减小。基于此，在加速度相同的前提下，当平台作Z向运动时，液压缸便可以输出较小的压力。

2.2 模拟器参数优化

在对六自由度舰船运动轨迹跟踪模拟器的2项关键指标，即液压缸的行程与受力进行优化时，可采取线性加权的方法，对现有的问题进行转化，使其变为单目标优化问题，这样做的目的是便于优化模型的确定，具体如下：

$ f(x) = {w_1}\cdot Stroke + {w_2} {\cdot} {F_{\max }} \text{。} $

式中： $ {w_1} $ 为模拟器液压缸行程的加权值； $ {w_2} $ 为模拟器液压缸最大受力的加权值。 $ {w_1} $ 和 $ {w_2} $ 的权重分别取0.75和0.25；Stroke取1.0 m； $ {F_{\max }} $ 取31 000 N。依据模拟器参数的取值范围，确定具体的约束条件，即约束条件R为1.6～2.8 m；r为1.3～2.0 m，h为2.3～3.2 m。除上述约束条件外，还应将上铰转轴与液压缸之间的夹角 $ \gamma $ 作为约束条件。这是因为 $ \gamma $ 的取值不宜过小，以免棱边产生相互干涉的情况。为防止干涉问题的产生，结合机械设计所需的刚度，对 $ \gamma $ 值加以确定，即大于40°。

$ {F_{\max }} $ 是整个目标函数中复杂程度最高的一项，受到一些因素的限制，使得 $ {F_{\max }} $ 的导数项难以获取。因此，传统的优化方法无法对目标函数求解。由于遗传算法能够通过收敛得到全局最优解，所以选用该算法对模拟器进行参数优化。具体步骤如下：先进行编码并确定搜索空间，本次优化中，编码采用实数，结合约束条件，确定遗传算法的搜索边界；随后初始化过程，并定义整数pop，以此作为染色体的个数；对函数做系统评价，为种群内的染色体设定概率，使其被选中的可能性更高，其中最好的染色体为i=1，而最好染色体的选择概率为a；参数经过迭代达到终止条件后，便可终止运行，最终得到的结果即为最优解，这个解就是最佳的模拟器参数。

2.3 运动轨迹跟踪算法验证

对本文提出的六自由度舰船运动轨迹跟踪算法进行实验验证，从运动轨迹两端的起始点和终止点之间的路线上确定约束点，利用仿真软件Matlab实验验证。实验过程如下：规划运动轨迹，通过算法得到各关节角度值，将其转换为脉冲量，用于驱动各关节运动，促使模拟运动轨迹按照既定路径运动。运动轨迹的驱动装置为伺服电机，需要确定各轴向的电机脉冲值，即S轴脉冲值为1 341 s，L轴脉冲值为1 832 s，U轴脉冲值为1 377 s，R轴脉冲值为910 s，B轴脉冲值为780 s，T轴脉冲值为520 s。六自由度转过的角度与脉冲值之间是线性关系。

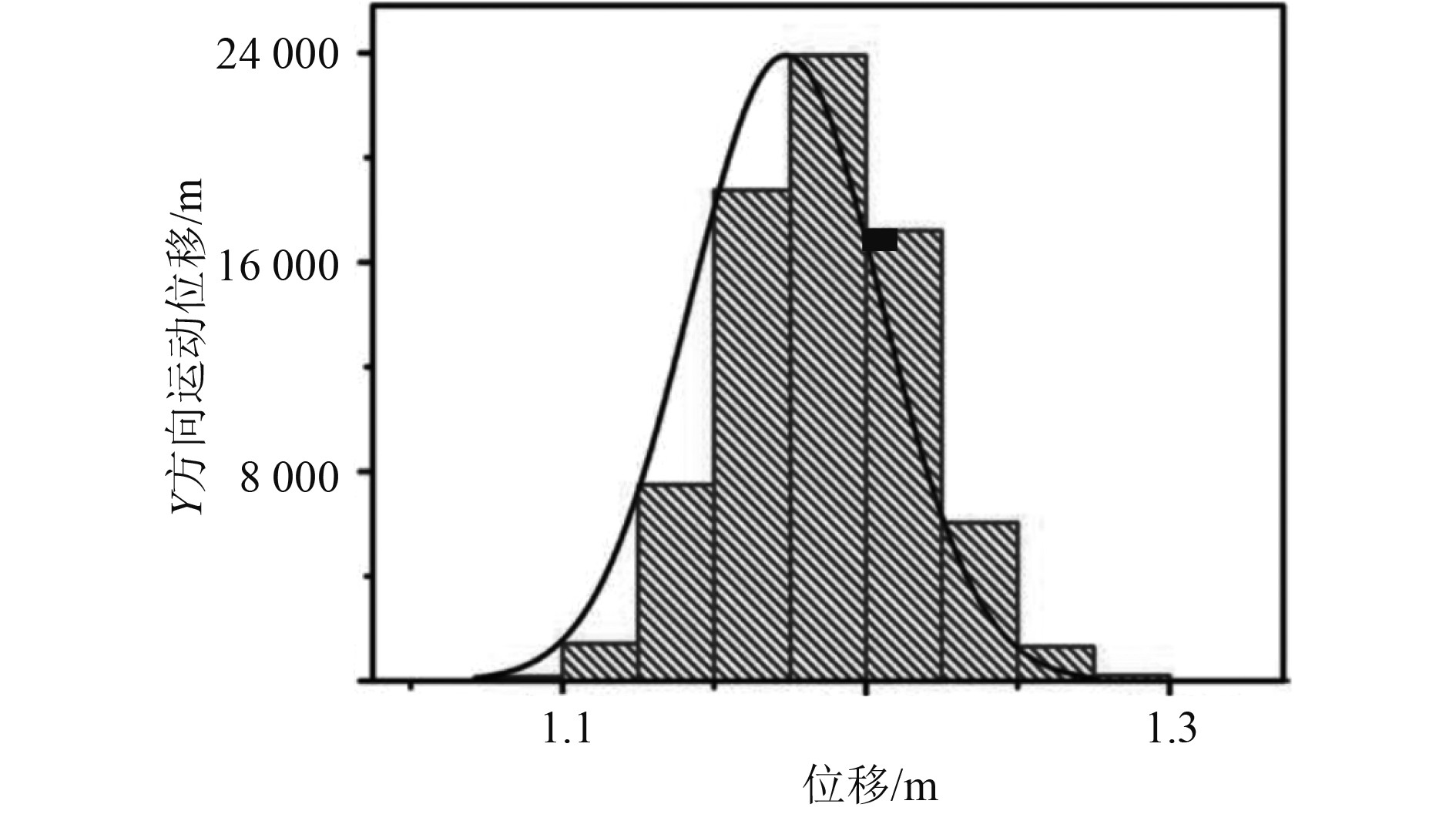
根据实验条件验证点到点的运动规划，利用仿真软件功能模拟两点间的直线运动，建立起直角坐标系，六自由度舰船运动受力仿真模拟图如图6所示。将直角坐标系转换为三维坐标系，模拟舰船运动轨迹，基于三维坐标系的六自由度舰船运动轨迹仿真模拟图如图7所示。仿真结果表明，正弦轨迹上的路径点越多，运动轨迹越清晰。本文提出的运动轨迹算法能够精确计算出轨迹上的约束点，并对插值时间进行修正，保证达到运动轨迹跟踪的精度要求。

3 结　语

基于遗传算法的六自由度舰船运动轨迹跟踪平台具备良好的节能性、安全性和可控性，能够精准模拟舰船在海洋航行环境下的摇摆情况，提升舰船运动机构模拟器的技术水平。在运动轨迹跟踪模拟器的设计中要对遗传算法进行优化改进，通过大量计算得出最优解，提高运动轨迹跟踪模拟的精确性。