0 引　言

集成电机泵喷推进器与常规泵喷推进器相比结构上最大的区别在于其导管内加装电机，电机转子与叶轮叶片叶稍面无缝连接，定子安装在导管内。这种结构使其具有灵活性、可靠性高、结构紧凑、振动和噪声低的优势^[1]。集成电机泵喷推进器的结构使得电机的定子内表面和转子的外表面间存在间隙，当推进器工作时，水流流过间隙时，除了可以冷却电机定子等发热部件，一定程度上由于水流与空气存在粘度与密度差，会在电机转子与叶轮叶片的连接部位（电机轮缘）产生较大的摩擦扭矩，这样会使得推进器在高速旋转时产生较大的功率损耗。所以为了设计低功率损耗与散热性能好的集成电机泵喷推进器，其间隙流动规律研究显得非常必要。

间隙流动规律的研究主要有经验法和数值分析2种方法。国外学者对间隙流动导致的轮缘扭矩损耗多集中在用经验法评估，Michael^[2]将间隙流的摩擦扭矩分为3个部位，即轮缘外表面、内表面和间隙进出2个轮缘端面，不同部位用不同的经验公式估算。其中轮缘外表面摩擦扭矩经验公式是Bligen ^[3]在不同湍流模型下研究扭矩系数与扭矩之间的关系时提出的；Daily^[4]研究了不同雷诺数时，扭矩随轴向间隙比如何变化的，并且提出了轮缘进出端面摩擦扭矩的经验公式，同时提出应用平板摩擦阻力公式判断内表面摩擦扭矩的大小。目前，国内关于集成电机泵喷推进器间隙流动规律模拟研究公开的相关研究资料较少。曹庆明等^[5-7]首先对轮缘推进器由于间隙流动引起的轮缘扭矩损耗进行了试验验证分析，然后研究了轮缘推进器有无轴向压力差时间隙流动和摩擦扭矩的情况，并通过经验公式和数值方法进行了分析比较，提出了如何减小摩擦扭矩提高推进器效率。刘宝等^[8-9]首先对导管螺旋桨和轮缘驱动推进器水动力特性进行了数值研究比较，结果表明轮缘驱动推进器的间隙流动导致其整体效率低于导管螺旋桨。在此基础上，分析了不同径向和轴向间隙比、速度和压力对轮缘驱动推进器间隙流场的影响。结果表明，摩擦扭矩随间隙增大而增大，轴向与径力向间隙相互作用影响摩擦扭矩，电机产生的热量在间隙流中迅速消散。柯永胜等^[10]研究了不同转速和不同进速系数下轮缘推进器间隙流道流量和轴向压差情况，得出间隙内轴向压差、轴向流量与周向流量随着转速的增大而增大，且周向流量要整体大小轴向流量；间隙流体周向流动会产生旋涡，而轴向压差会抑制旋涡的产生，因此为了改善轮缘推进器电机的散热，需要增大间隙流体轴向运动，减小周向运动。翁凯强等^[11-12]为了准确地预报泵喷推进器水动力性能，考虑泵转子尖端和导管内部之间存在的间隙区域流体粘度的影响，并且构建了间隙流动模型，研究发现在间隙流动的影响下，推进器导管的水动力性能与压力分布更加趋向于粘流计算结果，确定了最佳间隙高度为整个间隙高度的0.98~1.0倍。鹿麟等^[13]对E779A桨进行了非空化与空化数值模拟，在此基础上，研究了不同叶顶间隙对泵喷推进器水动力性能的影响规律，发现未空化与空化时，推进器整体效率都随着间隙尺寸的增大而降低，空化时推进器效率下降幅度相对于未空化时更小。

当集成电机泵喷推进器以高速旋转时，通常在间隙区域中产生涡流。该涡流与主要通道流体流动相互作用，影响推进器的水动力性能，导致转子系统的主要能量损失。本文为了研究间隙流动对自主设计的集成电机泵喷推进器水动力性能的影响，确定不同间隙几何参数时的推进器轮缘摩擦扭矩，分析转子、定子以及导管的敞水性能情况。

1 数值计算方法 1.1 几何模型

基于升力法设计转子叶片，其中叶轮翼型采用的是NACA4409翼型，修正系数法设计定子叶片，导叶翼型采用的是443翼型，由于要安装电机，采用No.19A型导管。为了精确模拟来流，在转子轴前部设计个半椭球体导流帽，集成电机泵喷推进器水力模型如图1（a）所示。推进器叶轮直径D=140 mm，叶轮和导管叶片数分别为5和7，比转速为600。电机转子与导管之间存在轴向和径向间隙，见（图1（b）），入流端轴向间隙宽度为 $ {l_{{\rm{in}}}} $ ，出流端轴向间隙宽度为 $ {l_{{\rm{out}}}} $ ，径向间隙高度为 $ h $ ，转子叶片半径为 $ r $ ，轮缘外径为2 $ {r_1} $ ，导管定子内表面直径为2 $ {r_2} $ 。研究径向间隙时，保持导管定子内表面直径不变，通过改变轮缘外径来获得不同径向间隙几何参数，轴向间隙保持2 mm不变；研究轴向间隙时，保持轮缘长度不变，通过改变导管放置电机中间部分的长度来获得不同轴向间隙几何参数，径向间隙保持2 mm不变，不同间隙几何参数设置如表1所示。

1.2 基本控制方程

在本文研究中，三维不可压缩流体模型用于数值模拟，因此对计算域采用雷诺平均N-S方程以及SST $ k - \omega $ 湍流模型进行数值模拟计算，连续性和动量方程如下^[14]：

$\frac {{\partial {\rho _m}}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{\mu _j}} \right)}}{{\partial {x_j}}} = 0, $

(1)

$ \frac{\partial }{{\partial t}}\left( {{\rho _m}{\mu _i}} \right) + \frac{{\partial \left( {{\rho _m}{\mu _i}{\mu _j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\nu + {\mu _t}} \right)\left( {\frac{{\partial {\mu _i}}}{{\partial {x_j}}} + \frac{{\partial {\mu _j}}}{{\partial {x_i}}}} \right)} \right] 。$

(2)

式中： $ {\rho _m} $ 为流体的密度， $ {\mu _i} $ 与 $ {\mu _j} $ 分别为 $ i $ 方向与 $ j $ 方向上的速度分量， $ \nu $ 为动态粘度， $ {\mu _t} $ 为湍流粘度。

1.3 间隙模型

根据Bligen在不同湍流模型下研究扭矩系数与扭矩之间关系时提出的同轴圆柱、内旋转圆柱和外静止圆柱的摩擦扭矩经验公式，根据雷诺数的大小把湍流状态分成两部分，其摩擦扭矩系数为：

$ {C_M} = 1.03{\left( {h/{r_1}} \right)^{0.3}}{{{{Re}}} ^{ - 0.5}}，\left ( {400 ＜{{{Re}}} ＜ 10000} \right) ，$

(3)

$ {C_M} = 0.065{\left( {h/{r_1}} \right)^{0.3}}{{{{Re}}} ^{ - 0.2}}，\left( {{{{{{Re}}}}} ＞ 10000} \right) ，$

(4)

$ {C_M} = {M \mathord{\left/ {\vphantom {M {0.5{\text{π}} \rho {\omega ^2}}}} \right. } {0.5{\text{π}} \rho {\omega ^2}}}{r_1}^4h 。$

(5)

式中：Re为径向间隙雷诺数， $ {Re} = {{\rho \omega {r_1}h} \mathord{\left/ {\vphantom {{\rho \omega {r_1}h} \nu }} \right. } \nu } $ ； $ \nu $ 为动态粘度； $ \ \rho $ 为流体密度； $ \omega $ 为角速度； $ M $ 为内旋转圆柱外表面的摩擦扭矩。

Daily为了进一步研究同轴圆柱、内旋转圆柱和外静止圆柱的摩擦扭矩，进行一系列的实验研究扭矩随轴向间隙比是如何变化的。结果表明，摩擦扭矩只与间隙比和雷诺数有关，在一定的轴向间隙比下，湍流状态可分为混合层流、分离层流，混合湍流与分离湍流。当轴向间隙比 $ l/{r_1}> 0.05 $ 时，间隙内的流动状态为分离层流或者湍流，当轴向间隙比为 $ 0.01 < l/{r_1} < $ $ 0.05 $ 时，间隙流动状态为混合湍流，此时进出端面摩擦扭矩系数为：

$ {C_M} = 0.08{\left( {l/{r_1}} \right)^{ - {1 \mathord{\left/ {\vphantom {1 6}} \right. } 6}}}{{Re} _l}^{ - 0.25} ，$

(6)

$ {C_M} = {{2M} \mathord{\left/ {\vphantom {{2M} {\rho {\omega ^2}}}} \right. } {\rho {\omega ^2}}}{r_1}^5 。$

(7)

式中： $ l/{r_1} $ 为轴向间隙比； ${{Re} _l} $ 为雷诺数， $ {{Re} _l} = {{{r_1}} \mathord{\left/ {\vphantom {{{r_1}} \nu }} \right. } \nu } $ ； $ M $ 为端面的摩擦扭矩。

1.4 网格划分与边界条件

根据本文所研究的物理问题可知，计算域分为外部流场、转子系统和定子系统，转子与定子系统嵌于外部流场域中，其中只有转子系统是旋转域，而另外的是静止域，2个区域通过滑移网格技术模拟之间的相互作用。为了使数值计算更符合实际，采用与泵喷同轴的圆柱形为计算域，如图2所示。泵喷转子的最大直径是D，外部流场域计算域的入口与出口边界远离转子都为10D，外部流场域的直径为4D。

对集成电机泵喷推进器按照结构组成进行分块，其中对叶轮叶片与导叶采用贴体网格生成网格，其余子块分别用结构网格进行划分，后耦合成总体网格系统。在网格耦合时，要保证子块之间分界面处的网格光滑连续。计算区域整体网格如图3所示，整个计算域有3605181个网格节点。

要得到集成电机泵喷推进器间隙流动的数值模拟，必须设置合理的边界条件，进出口与壁面的边界设置如图3所示，湍流强度设置为默认值，旋转与静止域交界面之间的耦合由Frozen Rotor交界面实现，流场流体物理参数液体温度为25°C，流体密度为998.71 kg/m³，运动黏性系数为1.06 kg/m³。应用Ansys Fluent软件对集成电机泵喷推进器进行数值模拟，应用RANS方法求解三维流场，并采用SST $ k - \omega $ 湍流模型封闭。采用有限体积法对方程组进行离散，速度与压力耦合应用Simplec算法处理，空间离散采用高分辨率混合差分格式，时间离散采用1阶欧拉后插格式。

2 计算结果分析 2.1 数值方法验证

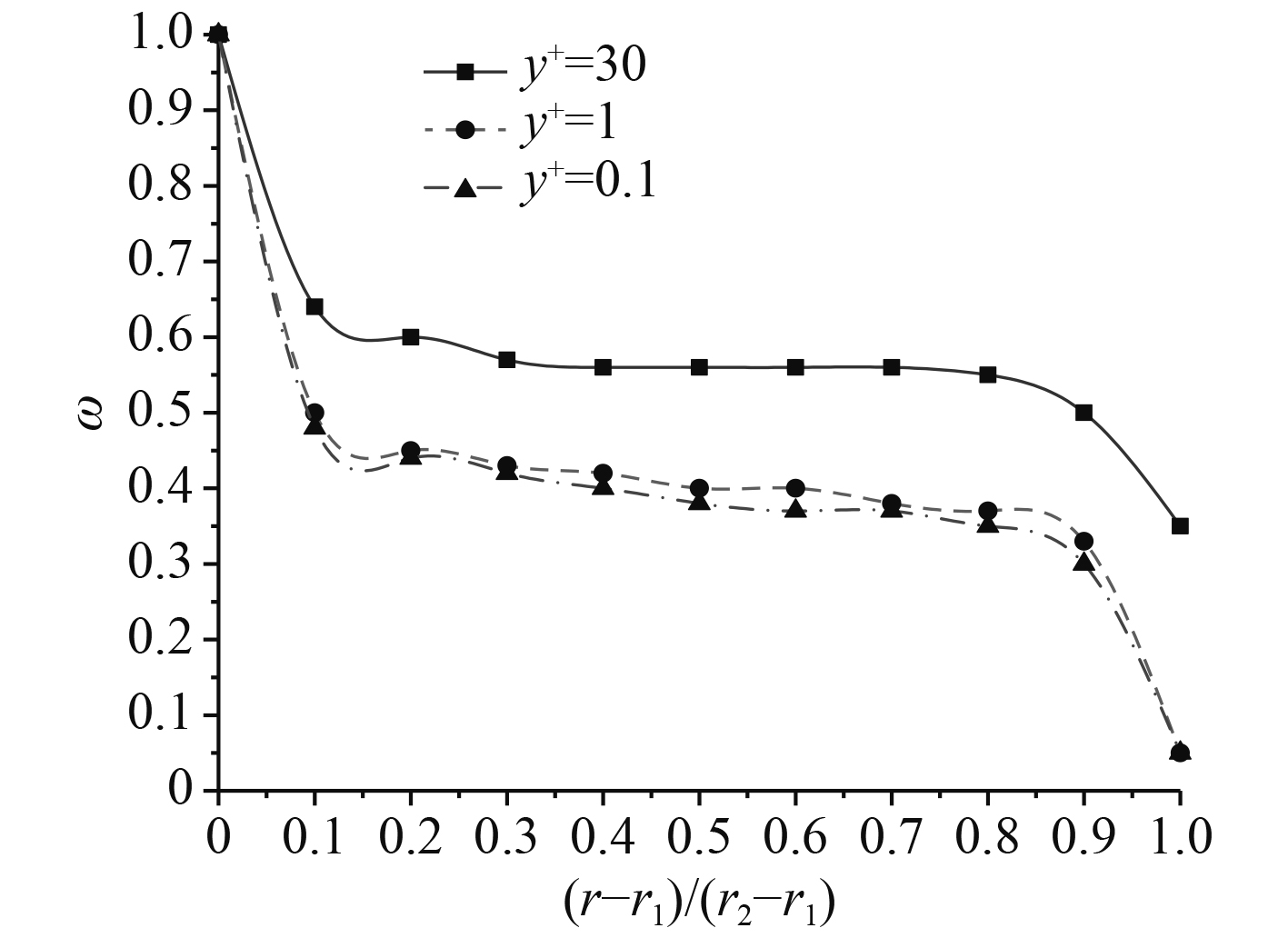
为了验证数值计算模型以及计算网格的正确性，先选取对轴向与径向间隙分别为2 mm进行计算。根据上述间隙模型发现所研究参数模型间隙内的流动状态为混合湍流，考虑到实际情况，必须对间隙进行细化，以保证计算结果的正确性。按照网格收敛准则生成3组不同 $ {y^ + } $ 的网格，分别为0.1，1，30。一般来说，对于高雷诺数模型（如k-Epsilon模型、雷诺应力模型等）， $ {y^ + } $ 一般以接近30为佳，对于低雷诺数模型（如 $ k - \omega $ 模型、SA模型、LES等），以接近于1为佳，所以在估算第1层网格时，按选择使用的湍流模型的不同，通常取30或1进行估算。得到轮缘中心处径向间隙内周向速度在这3种网格时的情况如图4所示。当 $ {{\left( {r - {r_1}} \right)} \mathord{\left/ {\vphantom {{\left( {r - {r_1}} \right)} {\left( {{r_2} - {r_1}} \right)}}} \right. } {\left( {{r_2} - {r_1}} \right)}}>0.6 $ 时， $ {y^ + } $ =0.1与 $ {y^ + } $ =1的径向间隙内周向速度相差不多，加上本文选取的流动模型，因此选取 $ {y^ + } $ =1作为计算的网格。

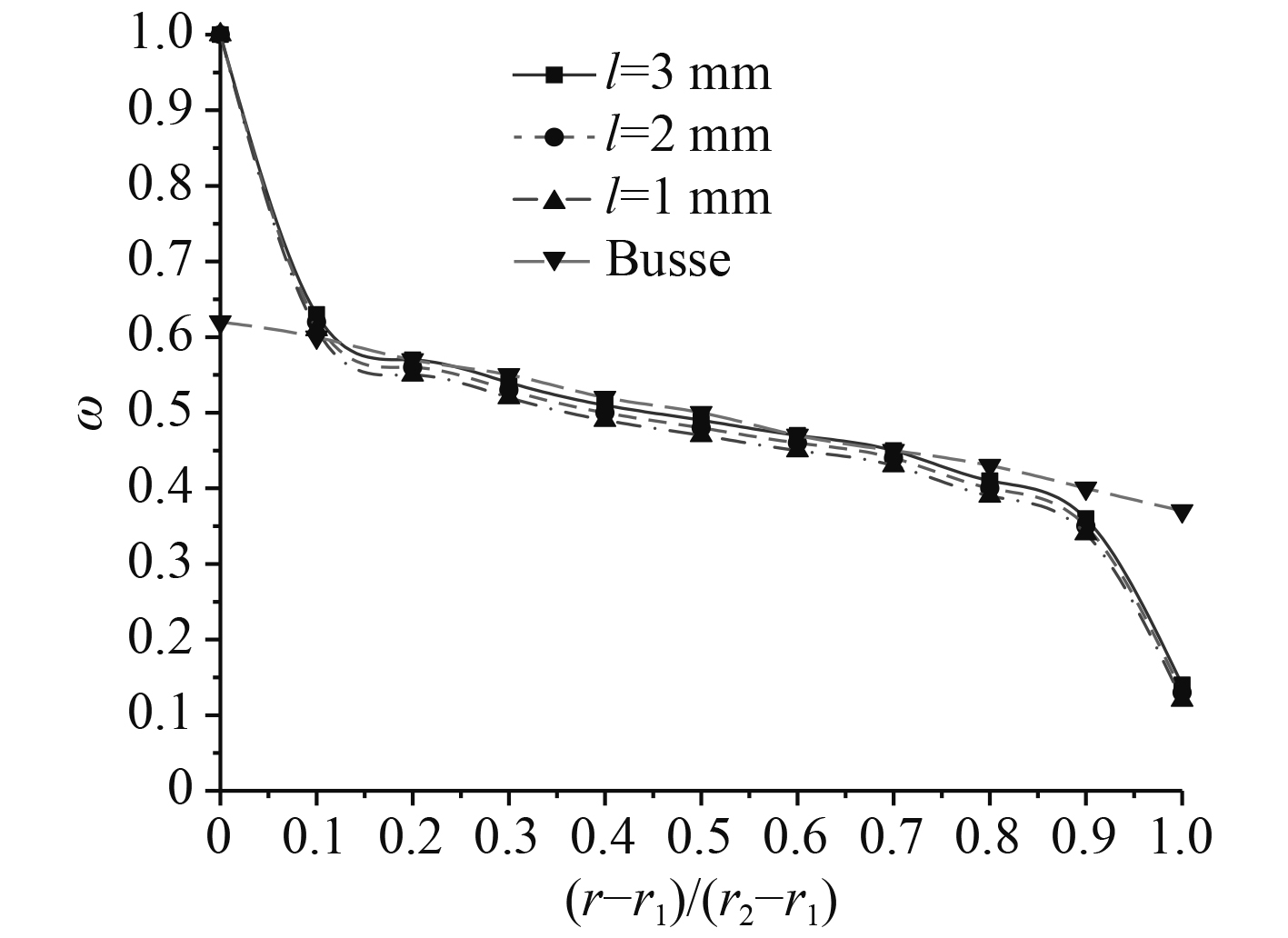
同时还对轴向间隙分别为3 mm，2 mm，1 mm，径向间隙为2 mm时的轮缘中心处径向间隙内周向速度进行计算，这些结果与Busse^[15]经验公式进行比较，如图5所示。可以发现计算的角速度与Busse经验公式吻合度较好，说明本文的数值模型可行。

2.2 不同参数下间隙扭矩的变化规律 2.2.1 设计间隙时不同参数下间隙扭矩的变化规律

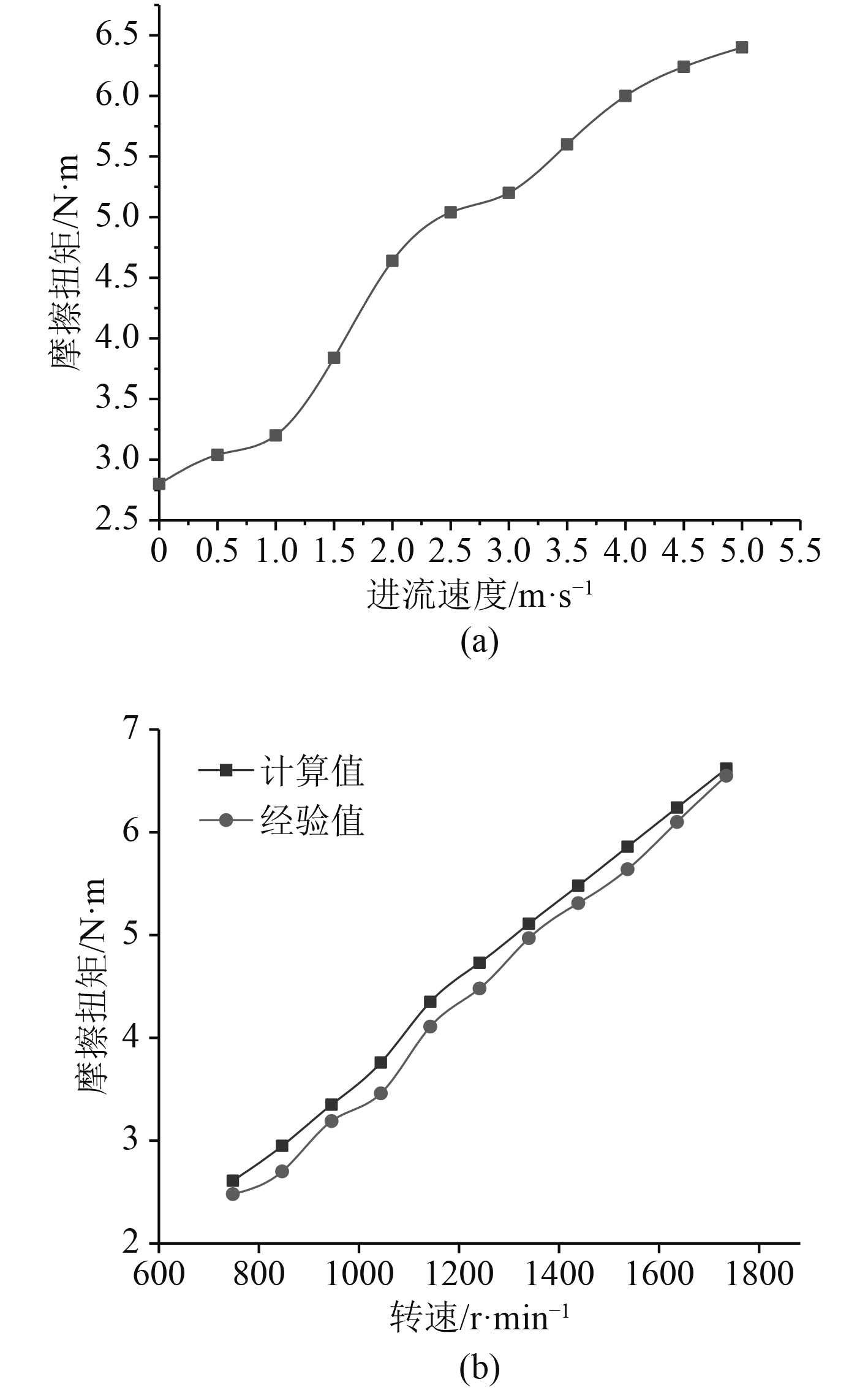
当轴向与径向间隙分别为2 mm时，推进器在额定转速1 250 r/min时，轮缘摩擦扭矩随着不同进流速度的变化情况如图6(a)所示。当推进器处于泊位状态时，轮缘摩擦扭矩在不同转速下的变化情况如图6(b)所示。同时，采用经验公式计算轮缘摩擦扭矩，并进行比较。

由图6(a)可知，轮缘摩擦扭矩随着进流速度的增加而增加，但进流速度达到一定大小时，不再增加。这是由于进流速度增大时，使得间隙边界层中的流体受到其他方向的剪切应力作用，会产生更大的轮缘摩擦扭矩，而当增大到一定值时，导致间隙边界层变化速度变慢，从而轮缘摩擦扭矩变大的速度也变慢。由图6(b)可知，当推进器处于泊位状态时，轮缘摩擦扭矩随转速的增大再增加。这是因为高转速时，雷诺数也大，所以根据轮缘摩擦扭矩的经验公式可知，扭矩也变大。图6(a)与图6(b)同样显示了与经验公式比较的结果，其变化趋势都一样，有一定的误差，经验结果小于计算结果。这是由于经验公式是独立分析不同区域的间隙流，忽视了不同区域间隙流的相互作用。

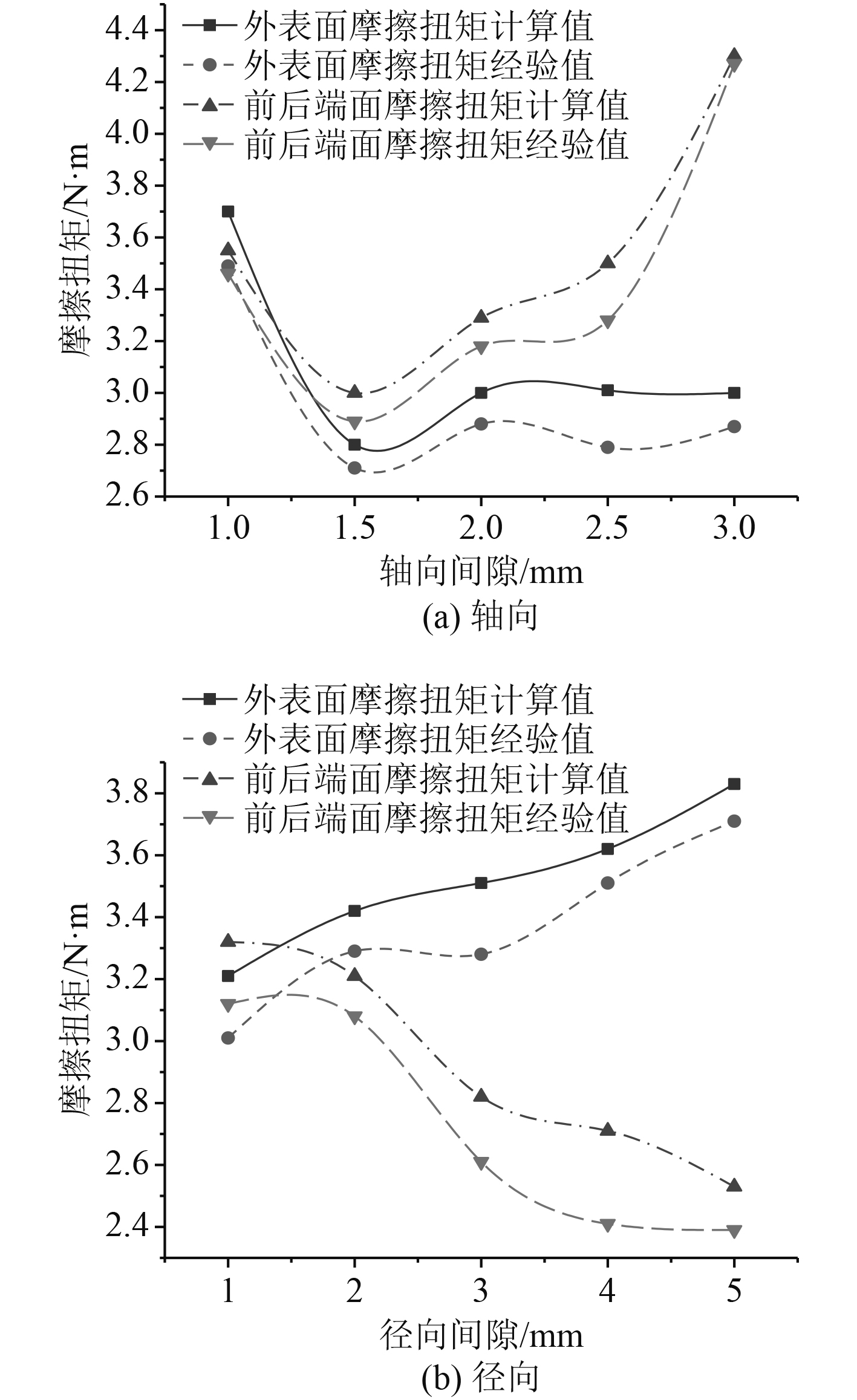
2.2.2 不同间隙尺寸下间隙扭矩的变化规律

根据表1所示的间隙尺寸，计算不同间隙尺寸下时轮缘摩擦扭矩，得到不同轴向、径向间隙尺寸时轮缘外表面摩擦扭矩 $ {M_1} $ 与前后端面摩擦扭矩 $ {M_2} $ 的变化情况。同时，采用经验公式计算轮缘摩擦扭矩，并进行比较，如图7所示。由图7（a）可知，当轴向间隙大于2 mm时，轮缘外表面摩擦扭矩 $ {M_1} $ 基本上保持稳定，而前后端面摩擦扭矩 $ {M_2} $ 是随着轴向间隙的增大而增大，在轴向间隙比较小，两者均随着间隙的增大而减小。由图7（b）可知，轮缘外表面摩擦扭矩 $ {M_1} $ 随着径向间隙的增大而增大，而前后端面摩擦扭矩 $ {M_2} $ 随着径向间隙的增大而减小。2种间隙尺寸下的计算结果与经验结果相比，计算结果总是高于经验结果，不过变化趋势都一样。因此，可通过减小轴向间隙，可减小间隙流动，降低轮缘的摩擦扭矩。

3 推进器水动力性能分析

为了方便计算结果的分析，对相关物理量作如下说明：进速比 $ J = {v \mathord{\left/ {\vphantom {v {(nD)}}} \right. } {(nD)}} $ ，转子、定子与导管推力系数分别为 ${{ K}_{{{{T_R}}}}} = {{{T_R}} \mathord{\left/ {\vphantom {{{T_R}} {\left( {\rho {n^2}{D^4}} \right)}}} \right. } {\left( {\rho {n^2}{D^4}} \right)}},{{ K}_{{T_S}}} = {{{T_S}} \mathord{\left/ {\vphantom {{{T_S}} {\left( {\rho {n^2}{D^4}} \right)}}} \right. } {\left( {\rho {n^2}{D^4}} \right)}}, {{ K}_{{T_D}}} = $ $ {{{T_D}} \mathord{\left/ {\vphantom {{{T_D}} {\left( {\rho {n^2}{D^4}} \right)}}} \right. } {\left( {\rho {n^2}{D^4}} \right)}}$ ，转子、定子转矩系数分别为 ${{ K}_{{Q_R}}} = $ $ {{{Q_R}} \mathord {\left/ {\vphantom {{{Q_R}} {\left( {\rho {n^2}{D^5}} \right)}}} \right. } {\left( {\rho {n^2}{D^5}} \right)}},{{ K}_{{Q_S}}} = {{{Q_S}} \mathord{\left/ {\vphantom {{{Q_S}} {\left( {\rho {n^2}{D^5}} \right)}}} \right. } {\left( {\rho {n^2}{D^5}} \right)}}$ ，推进器总推力、转矩系数分别为 $ {K_T} = {K_{{T_R}}} + {K_{{T_S}}} + {K_{{T_D}}},{K_Q} = {K_{{Q_R}}} + {K_{{Q_S}}} $ ，推进效率 $\eta = \left( {{{{{ K}_T}} \mathord{\left/ {\vphantom {{{{ K}_T}} {{{ K}_Q}}}} \right. } {{{ K}_Q}}}} \right) \cdot \left( {{J \mathord{\left/ {\vphantom {J {2{\text{π }}}}} \right. } {2\text{π} }}} \right)$ 。其中 $ v $ 为来流流速， $ n $ 为转子转速， $ D $ 为转子直径， $ {T_R},{T_S},{T_D} $ 分别为转子、定子与导管推力， $ {Q_R}和{Q_S} $ 分别为转子、定子转矩。

3.1 间隙流动对转子、定子以及导管的敞水性能的影响结果分析

为了更加准确地了解集成电机泵喷推进器的水动力性能，分析间隙流动模型（轴向与径向间隙分别为2 mm）对集成电机泵喷推进器转子、定子以及导管的敞水性能的影响，同时与无间隙流动模型进行比较，如图8所示。

可知，有间隙流动时，集成电机泵喷推进器转子、定子、导管以及整体的敞水性能相比无间隙流动时，都有更佳的结果，且随着转速的增加，两者差距变化稳定以及变化趋势一样。由图8还可得知，推进器整体的推力大部分来源于转子的推力，说明推进器的推力主要由转子产生的，且推进器的总扭矩基本上等于0，因为定子刚好平衡了推进器的扭矩，这样可避免航行器出现翻转、俯仰现象。

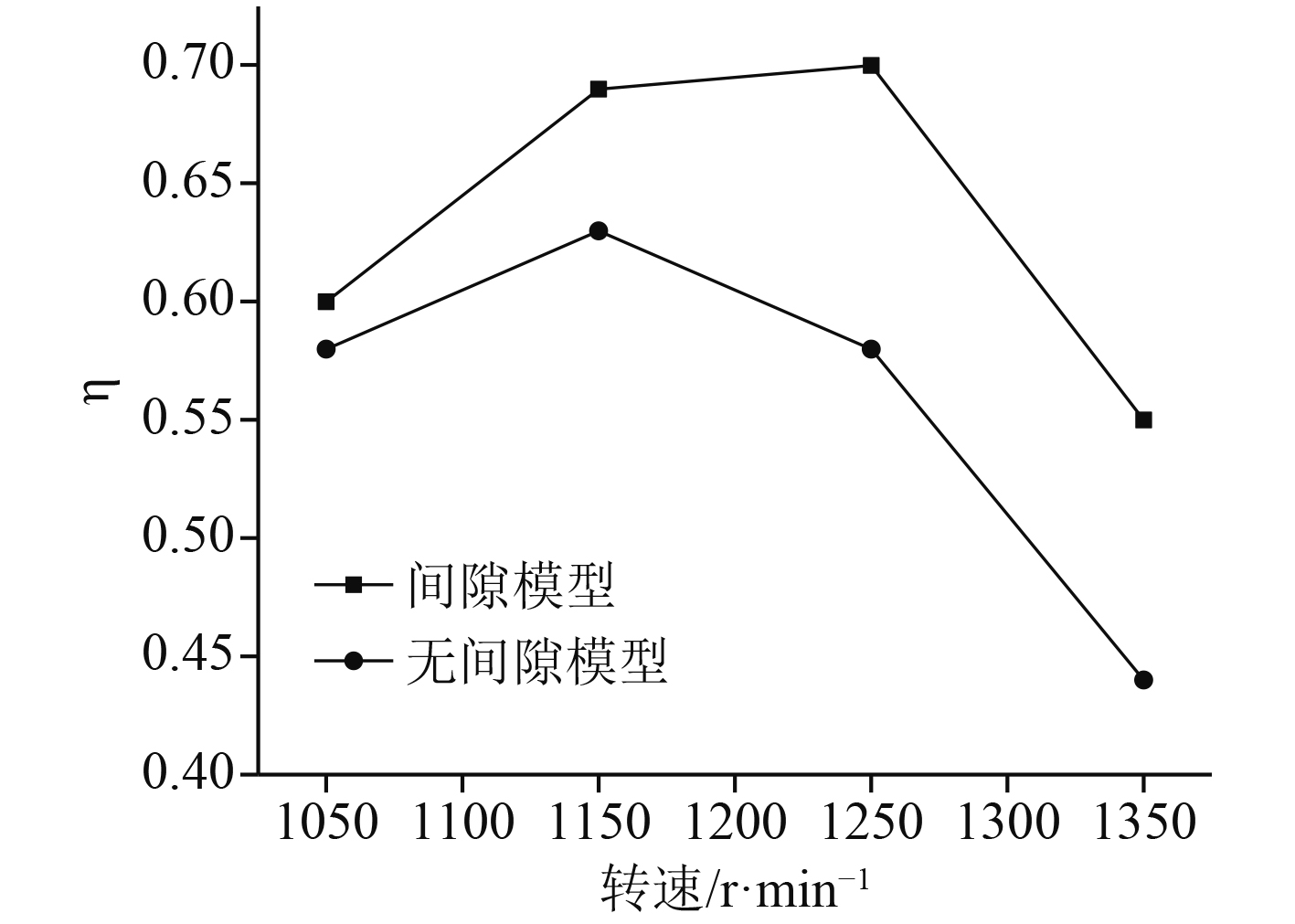
图9为集成电机泵喷推进器在有无间隙流动模型时效率曲线，可以得知有无间隙流动时效率都随着转速的增加先减小再增大。这是由于当转速大时，间隙处的流动更为激烈，导致效率的变化更为显著。有无间隙流动时效率变化趋势一样，有间隙模型时的效率总是大于无间隙模型，这也符合理论结果。

3.2 不同间隙尺寸下集成电机泵喷推进器水动力性能的结果分析

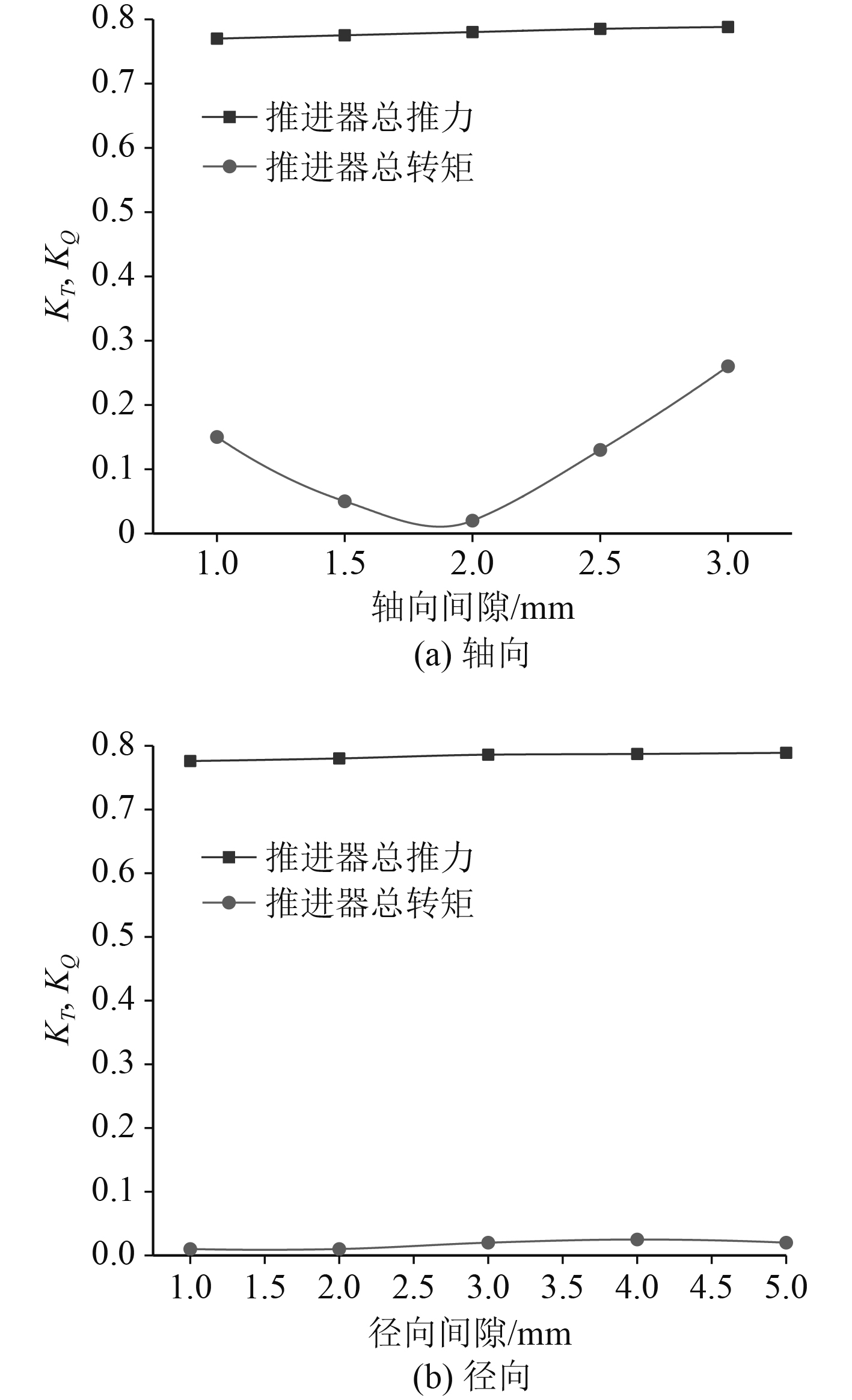
分析推进器在额定转速1 250 r/min时，不同间隙方案对集成电机泵喷推进器水动力性能的影响规律，如图10所示。可知，推进器总推力与轴向间隙、径向间隙的变化关联不大。这是由于轮缘外表面和前后端面的推力之和相互抵消，所以在间隙流动下，推进器的总推力随着轴向间隙与径向间隙的变化而保持稳定；推进器总转矩随着径向间隙的变化而基本上变化不大，而随着轴向间隙的变化是由于图7（a）的情况导致的。

4 结　语

本文研究间隙流动对自主设计的集成电机泵喷推进器水动力性能的影响，利用数值模拟方法，首先分析了不同参数下轮缘间隙中摩擦扭矩的变化规律，并与经验公式的结果进行比较。进而分析了有无间隙流动对推进器敞水性能的影响情况，在此基础上，分析了不同间隙参数对推进器敞水性能的影响规律。

1）在设计间隙尺寸时，轮缘摩擦扭矩随着进流速度的增加而增加，但是增长的过程不稳定；当推进器处于泊位状态时，轮缘摩擦扭矩随转速的增大再增加。

2）轮缘外表面摩擦扭矩基本上与轴向间隙大小无关，而前后端面摩擦扭矩是随着轴向间隙的增大而增大；轮缘外表面摩擦扭矩随着径向间隙的增大而增大，而前后端面摩擦扭矩随着径向间隙的增大而减小。可通过减小轴向间隙等方法达到降低轮缘的摩擦扭矩。

3）推进器水动力性能的变化趋势在有无间隙流动时一致，整体上，有间隙流动时，其性能更佳；有无间隙流动时效率都随着转速的增加先减小再增大，有间隙模型时的效率总是大于无间隙模型。推进器总推力与轴向间隙、径向间隙的变化关联不大；推进器总转矩随着径向间隙的变化而基本上变化不大，而与轴向间隙的关系与轮缘扭矩的规律相同。