空投气垫船是基于普通气垫船基础上设计的一种高速航行船舶,具有质量轻、灵活性好、航速高、水陆两栖能力强等优点,而且可以装备在飞机上根据需要从空中投放,有效提高了气垫船自身的航行时间和使用寿命,在海空配合军民两用领域有着广阔的应用前景。由于空投气垫船运行在空气、水2种介质的界面上,航行过程中受到静水稳态阻力以及风浪引起的动态阻力影响,其阻力构成十分复杂。
气垫船静水阻力特性的研究对于动力装置的选型和垫升性能的进一步提升有着重要意义。1983年全国船舶标准化技术委员会提出了气垫船静水阻力理论值计算方法[1],1991年邓佑生提出了一种关于气垫船动态阻力的估算方法[2],李林根等[3]对气垫船兴波阻力进行了具体的分析与计算。余泽爽[4]通过STAR-CCM+软件平台,对类似于气垫船的双M船水气两相特性、运动稳定性以及静水直航阻力等进行研究。付明玉等[5]通过Ansys Cfx平台采用雷诺平均Navier-Stokes方程及标准的
空投气垫船水面垫态航行总阻力主要分为稳态阻力和静态阻力,其各部分构成如图1所示。
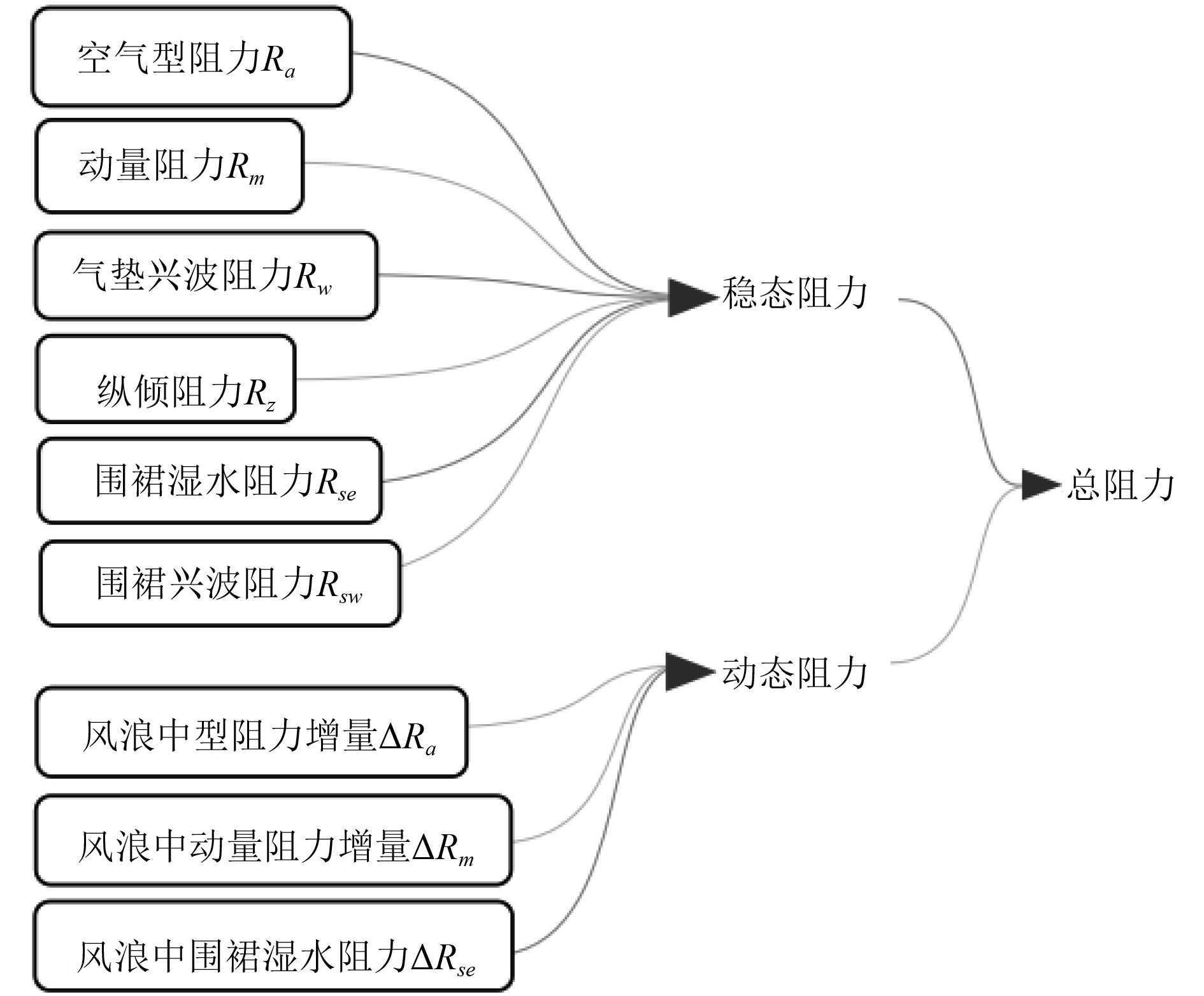
|
图 1 气垫船总阻力组成 Fig. 1 Total hovercraft resistance composition |
各分量阻力理论值可由式(1)~式(9)计算得出。
| $ {{{R}}_{{a}}} = \frac{1}{2}{C_a}{\rho _a}{S_a}{{{V}}^{{2}}} 。$ | (1) |
式中:Ca为空气型阻力系数,取空投气垫船Ca=0.45;空气密度ρa=1.25 kg/m3;V为船速,m/s,Sa为气垫船垫升态正投影面积,m²。
| $ {{{R}}_{{m}}} = {\rho _a} \cdot {Q_f} \cdot {{V}} 。$ | (2) |
式中:Qf为全船风机流量,m³/s。
| $ {{{R}}_{{w}}} = {C_w} \cdot \frac{{P_c^2 \cdot {B_c}}}{{g \cdot {\rho _w}}} 。$ | (3) |
式中:Pc为气垫压力值,Pa;Bc为气垫宽度,m;ρw为水密度,kg/m³;气垫兴波系数Cw可由纽曼图谱插值法取得。
| $ {{{R}}_{{z}}} = W \cdot \alpha 。$ | (4) |
式中:W为船重,N;α为水平面与围裙底线所在平面的夹角,一般取α=0.25°。
| $ {{{R}}_{{{se}}}} = {K_1} \cdot {10^{ - 6}} \cdot {C_l} \cdot \sqrt {{S_c}} \cdot {q_w} \cdot {\left( {\frac{h}{{{C_l}}}} \right)^{ - 0.34}}。$ | (5) |
式中:K1为气垫船围裙湿水阻力系数值,其计算公式为
| $ {{{R}}_{{{sw}}}} = \left[ {2.817 \cdot {{\left( {\frac{{{P_c}}}{{g{L_c}}}} \right)}^{ - 0.26}} - 1} \right] \cdot {R_w},$ | (6) |
| $ \Delta {{{R}}_{{a}}} = {C_a} \cdot \frac{{{\rho _a}{{\left( {V + {V_b}} \right)}^2}}}{2}{S_a} - {R_a}。$ | (7) |
式中:Vb为风速,m/s。
| $ \Delta {{{R}}_{{m}}} = {\rho _a} \cdot {{\text{Q}}_f} \cdot {V_b},$ | (8) |
| $ \Delta {{{R}}_{{{se}}}} = {q_w} \cdot {C_l} \cdot \sqrt {{S_c}} \cdot 2 \times {10^{ - 4}}{\left[ {\frac{{2{H_w}}}{{1.6\left( {{H_c} + {H_f}} \right)}}} \right]^{{5 \mathord{\left/ {\vphantom {5 3}} \right. } 3}}}。$ | (9) |
式中:Hw为有义波高,m;Hc为气垫高度,m;Hf为围裙手指高度,m。
2 数值模拟 2.1 实体建模三维建模精确性直接关系到数值模拟的准确性与可靠性,通过空投气垫船的相关设计参数以及二维图纸,利用CATIA三维建模软件按照实船尺寸建立空投气垫船实体模型;为提高仿真效率,对船体进行适当简化,所建三维模型如图2所示。
|
|
表 1 空投气垫船参数 Tab.1 Air drop Coverket parameters |

|
图 2 空投气垫船三维模型 Fig. 2 3D model of air hovercraft |
为了更加真实模拟空投气垫船在静水中匀速航行状况,将流体计算域出口面定义为压力出口,其余各面均设置为速度入口,船体表面设置为不可滑移壁面。边界条件设置如图3所示。
采用雷诺平均连续方程求解瞬态的粘性绕流场的方法,选择标准
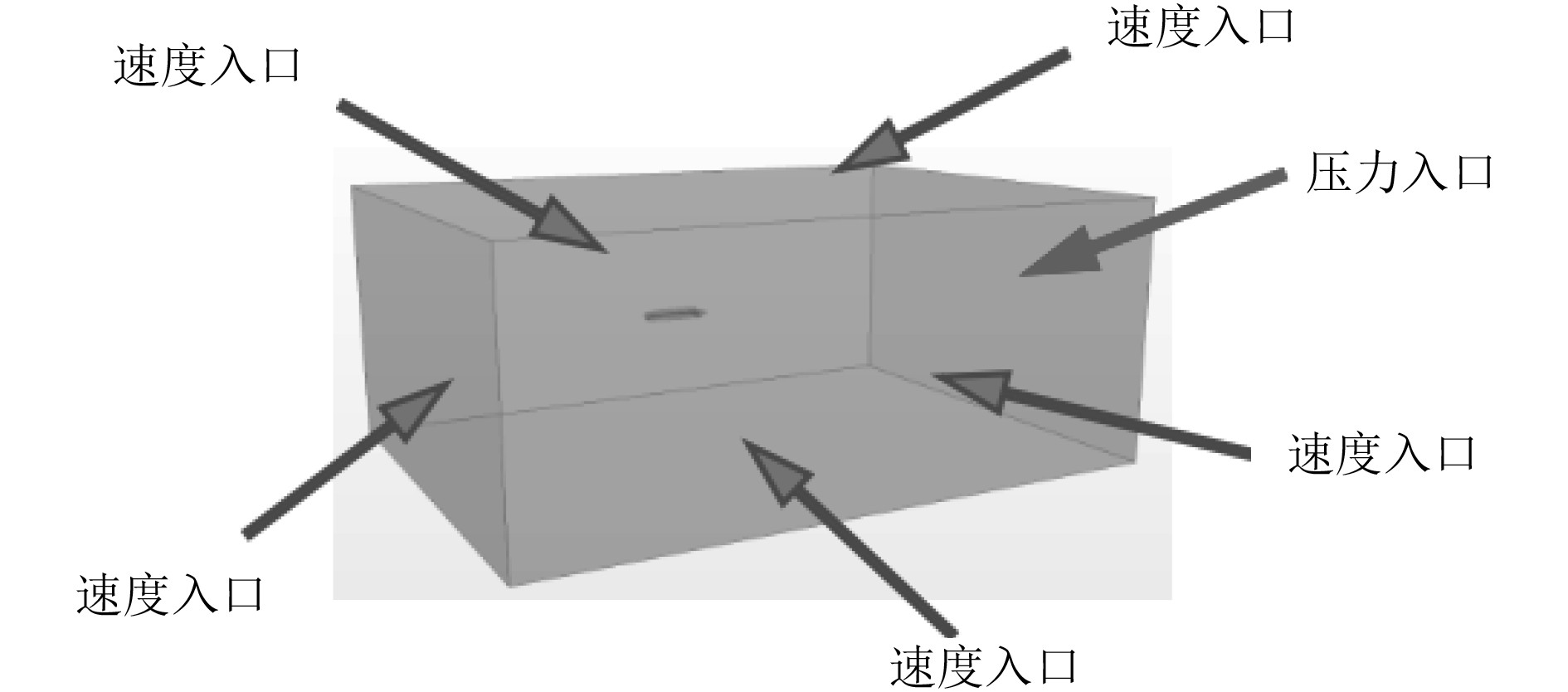
|
图 3 计算域边界条件 Fig. 3 Calculate the domain boundary conditions |
利用STAR-CCM+平台强大的流体计算能力,创建计算域作为虚拟拖曳池,以此来模拟船舶性能测试试验池,选择适用于外部流动的切割体网格形式,边界层选择棱柱层形式,层数为6。又由于空投气垫船航行时在空气和水的交界区域运动,因此以水面作为自由界面;而且在航行过程中不仅受到气动阻力,底部围裙有一定的吃水深度,必然产生以兴波阻力和湿水阻力为主的水动阻力,故而在流场网格划分时需创建5个加密区域,分别是船体外围、首部、尾部、自由界面处、开尔文波形区,利用STAR-CCM+平台强大的重叠网格功能进行处理,流场网格创建完成后共19885161个网格单元,如图4所示。

|
图 4 计算域网格 Fig. 4 Computational domain grid |
为了从本质上研究此类气垫船在静水中的航行阻力特性,将航速转换成无量纲的傅汝德数
| $ {{{F}}_{{r}}} = {{{V}} \mathord{\left/ {\vphantom {{\text{V}} {\sqrt {{\text{g}} \cdot {{L}}} }}} \right. } {\sqrt {{{g}} \cdot {{L}}} }} 。$ | (10) |
式中:V为空投气垫船航速,m/s;
1)兴波
图5为空投气垫船在静水中航行时的自由界面兴波图。可以看出,随着航速增加即傅汝德数德增大,气垫船兴波波长逐渐增大,水下兴波最深处区域逐渐远离船体,最形成稳定鸡尾涡所需时间延长,开尔文波系角逐渐减小。

|
图 5 各傅汝德数Fr对应兴波图 Fig. 5 EachFr corresponds to the wave-making |

|
图 6 各傅汝德数Fr对应水气两相云图 Fig. 6 EachFr corresponds to water-gas two-phase cloud map |
2)水气两相特性
图6为空投气垫船在不同傅汝德数的水气两相云图。可以看出,气垫船在静水中航行时,自由界面的变化情况、船体表面的水气分布情况、围裙的兴波以及空投气垫船绕流场的飞溅情况。研究表明,傅汝德数越大,气垫船的水气分布越复杂,兴起的波浪越大与受到的冲击越强,因此对船体的结构强度以及动力装置的性能要求更高。

|
图 7 各航速阻力曲线特征时刻图 Fig. 7 Characteristic time diagram of each speed resitance curve |
由图7和图8可知,空投气垫船在静水中航行时,Fr<1.817时,阻力曲线到达峰值所需时间随航速成正比,Fr>1.817时,阻力曲线到达峰值所需时间减小;船体所受力达到稳定状态时,阻力曲线将趋于收敛,其变化趋势与到达阻力峰值所需时间规律一致。
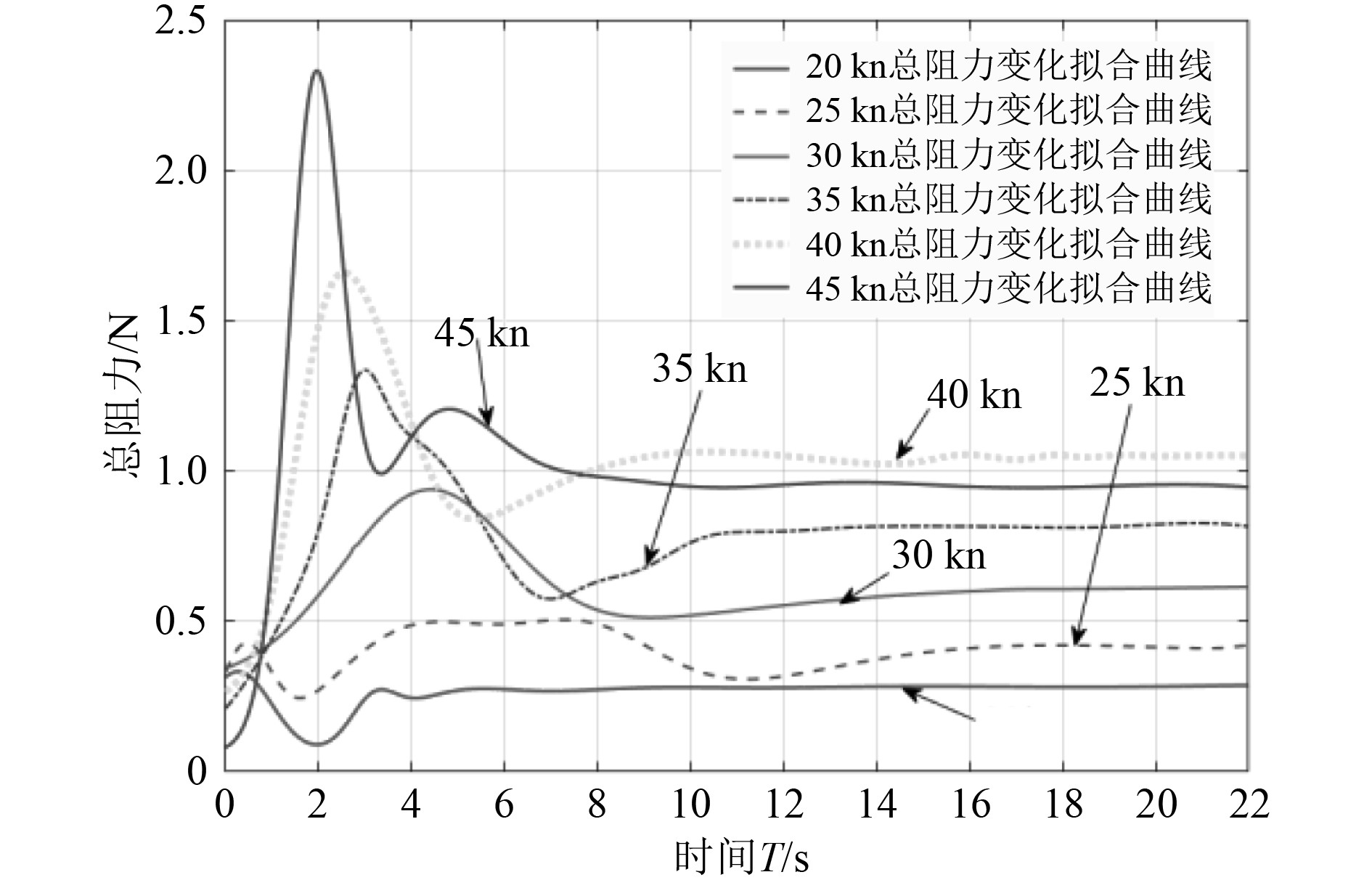
|
图 8 各航速总阻力变化监测 Fig. 8 Monitoring of total drag of each speed |
3)静水航行总阻力
用气垫船各阻力理论计算公式对空投气垫船所受气动阻力和水动阻力进行估算,由于在静水中匀速航行,因此将动态阻力忽略不计。仿真结果与理论值对比如表2所示,估算值与STAR-CCM+仿真对比如图9和图10所示。
|
|
表 2 仿真结果与理论值对比 Tab.2 Simulation results are compared with theoretical values |

|
图 9 不同航速总阻力理论值与仿真值对比 Fig. 9 The theoreyical value of the total drag of different speeds is compared with the simulation value |

|
图 10 不同Fr总阻力理论值与仿真值对比 Fig. 10 The theoreyical value of the total drag of different Fr is compared with the simulation value |
基于CATIA和STAR-CCM+平台,建立了空投气垫船虚拟拖曳池流场,对其静水中的兴波、气液两相情况以及总体阻力进行模拟,分析了该船在不同航速以及对应傅汝德数下的阻力变化规律。
1)随着航速的增加,空投气垫船到达阻力峰值的时间由长到短,拐点出现在Fr=1.817附近,越早跨越阻力峰值也就越早趋于平稳,最终无限收敛于一个定值即为所求总阻力。
2)空投气垫船在静水中形成稳定鸡尾涡的时间规律同上;但航速越高,兴起的波浪越大,绕流场更为复杂,开尔文波系角越小,自由面以下最深处涡团区域距离船体越远这有助于研究此类船舶的隐身性能和波系特征。
3)航速在20~40 kn时,空投气垫船所受总阻力与航速成正比,超过40 kn时,总阻力反而开始减小,这是由于气液两相特性使得船体底部空气体积分数增大、压力上升较快,气体最终从围裙底部逸出,流体运动达到动态平衡,气垫效应愈发显著;此外随着傅汝德数增大,船体表面开始出现部分区域水的体积分数小于1的现象,说明有外部空气进入围裙,有效减小了介质的粘性系数,从而起到减小摩擦阻力的作用。这也是气垫船具有高速性能的主导因素之一。
4)通过傅汝德数对无因次总阻力规律进行体现,同时用气垫船静水总阻力估算公式与STAR-CCM+仿真结果相对比,两曲线变化趋势相同,误差满足工程应用要求。验证了计算流体力学方法对此类气垫船的结构设计和阻力性能预报具有可靠性。
| [1] |
全国船舶标准化技术委员会. 气垫船静水阻力估算方法[S]. CB*/Z 329-83.
|
| [2] |
邓佑生. 气垫船原理与设计[M]. 北京: 国防科技图书出版, 1991.
|
| [3] |
李根林, 孙永权. 气垫船的兴波和兴波阻力(续)[J]. 船舶, 1999(2): 58-60. LI Gen-lin, SUN Yong-quan. Wave and wave resistance of hovercraft (continued)[J]. Ship, 1999(2): 58-60. |
| [4] |
余泽爽. 双M船水气两相特性与运动稳定性研究[D]. 武汉: 武汉理工大学, 2018.
|
| [5] |
付明玉, 张丽娜, 王建琴, 等. 基于CFX的全垫升气垫船船身空气动力模拟[J]. 华中科技大学学报 (自然科学版). 2013, 41(6): 90-93+127. FU Ming-yu, ZHANG Li-na, WANG Jian-qin, et al. CFX-based full-cushion lift hovercraft hull aerodynamic simulation [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition). 2013, 41(06): 90-93+127. |
| [6] |
赵宇南, 余又红, 贺星. 大型气垫船阻力特性仿真与影响因素分析[J]. 舰船科学技术, 2019, 41(19): 55-58. ZHAO Yu-nan, YU You-hong, HE-Xing. Simulation and analysis of large covercraft[J]. Ship Science and Technology, 2019, 41(19): 55-58. |
| [7] |
NIKSERESHT A H, ALISHAHI M M, EMDAD H. Complete flow field computation around an ACV(air-cushion vehicle) using 3D VOF with Lagrangian propagation in computational domain[J]. Computers and Structures. 2008, 86(7-8): 627-641.
|
| [8] |
BHUSHAN S, STERN F, DOCTORS L J. Verification and validation of URANS wave resistance for air cushi-on vehicles, and comparison with linear theory[J]. Journal of Ship Research. 2011, 55(4): 249-267.
|
 2022, Vol. 44
2022, Vol. 44
