2. 武汉第二船舶设计研究所,湖北 武汉 430205
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
操纵性是衡量航行器性能的重要指标。矢量推进器的出现使航行器操纵性能得到了显著提升,发展矢量推进技术越来越受到各国重视。矢量推进器是指喷口可以向不同方向偏转以产生不同方向推力的一种推进器,主要有螺旋桨式与喷水式2种类型[1-2]。目前相关研究的应用对象主要为AUV等小型潜器,其成果难以直接应用于大型水下航行器,如潜艇等。在小型潜器中,采用的并联机构实现矢量推进的方案,未考虑球面副难以密封、易磨损等工程问题[3-4];采用的齿轮系传动的螺旋桨式矢量推进方案,也存在齿轮系密封、传动轴振动等问题[5-6]。张凯等[7]提出的一种泵喷推进器加装尾喷管以实现矢量推进的方式,重点分析了喷管形状对操纵力的影响,并未涉及尾喷管操控机构的实现方案。
针对以上问题,提出一种采用多关节串联机构实现大通径喷管操控的方案,其结构简单,各关节间均为面接触,易于密封,承载能力强,能够适用于大型水下航行器。此类关节型式的串联机构在水下场合已有若干应用:文献[8]介绍水下救生用对接转裙的二关节串联结构,通过2个关节角的联合控制,可以使转裙对接面的角度满足最终对接控制要求;文献[9]介绍应用于飞机的三关节串联结构形式的推力矢量(3BSD)喷管及控制特性,其矢量控制关注于喷口在垂直面方向上由水平至下方90°的偏转控制。上述2种串联结构形式的对接面或喷管,虽然可以满足大流量的喷射需要,却无法满足水下矢量推进所要求的喷口在工作范围内向任意方向偏转的要求,即全向偏转能力要求。为此,提出具有2个冗余自由度的四关节串联机构的喷管,在分析其运动学特性及全方位偏转能力的基础上,给出实现喷口全方位摆动控制的各关节角的控制面。
1 机构运动学模型多关节串联型式的矢量喷管通过各关节转动角度的组合实现末端关节出口端面法向的变化,达到改变喷口推力矢量方向的目的。为便于描述,对各关节按入口到出口的顺序依次编号,各关节前后端面间的夹角是此类机构的主要参数,分别记为
建立喷管入口的静坐标系
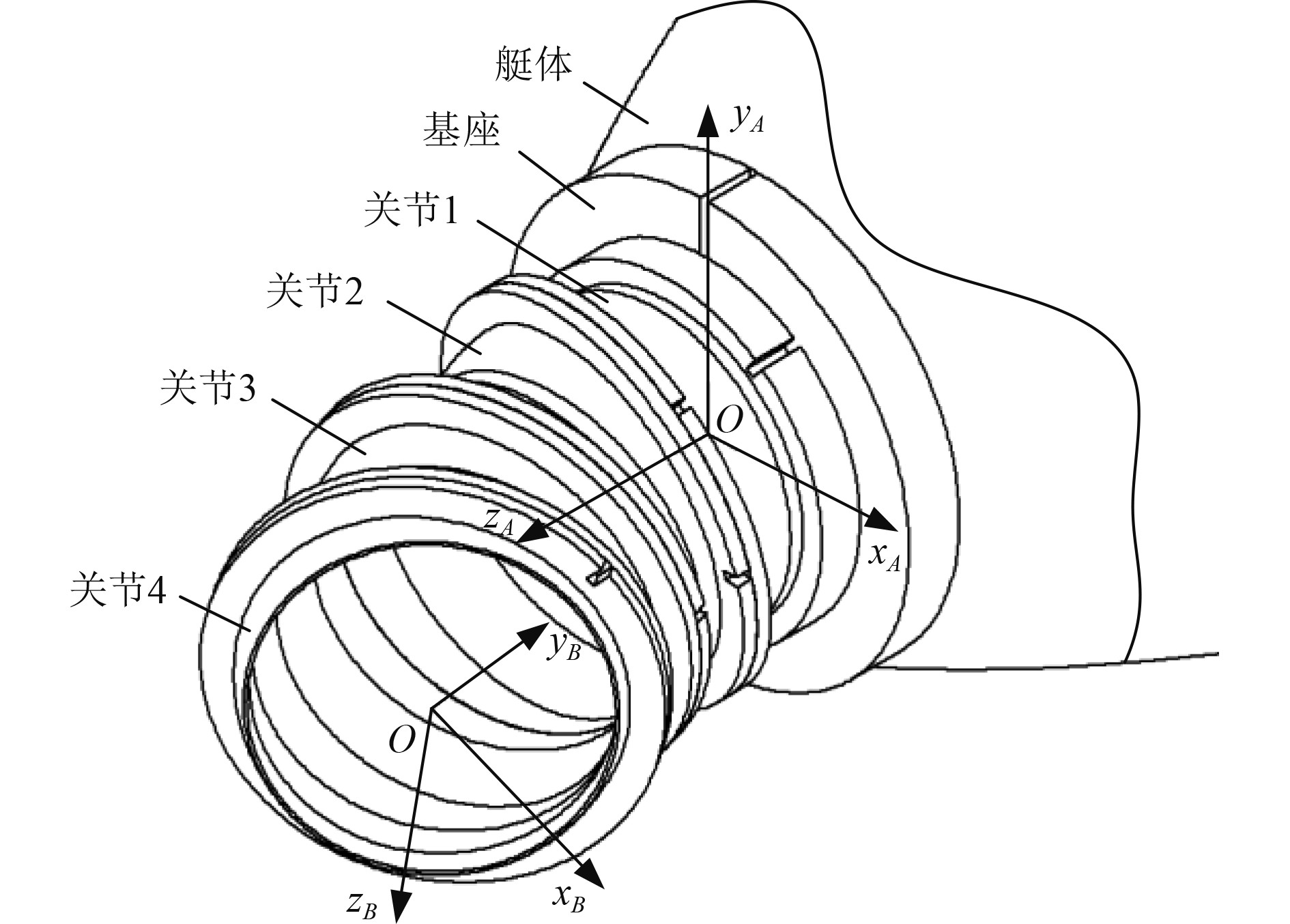
|
图 1 坐标系示意图 Fig. 1 Coordinate system diagram |
设各关节相对转动的角度为
| $ {{\boldsymbol{Z}}_B} = \prod\nolimits_{i = 1}^N {{{\boldsymbol{T}}_i}({\theta _i})} \cdot {\boldsymbol{z}} = {{\text{[}}{b_1},{b_2},{b_3}]^{\text{T}}}。$ | (1) |
式中:
喷口法矢量方向,即
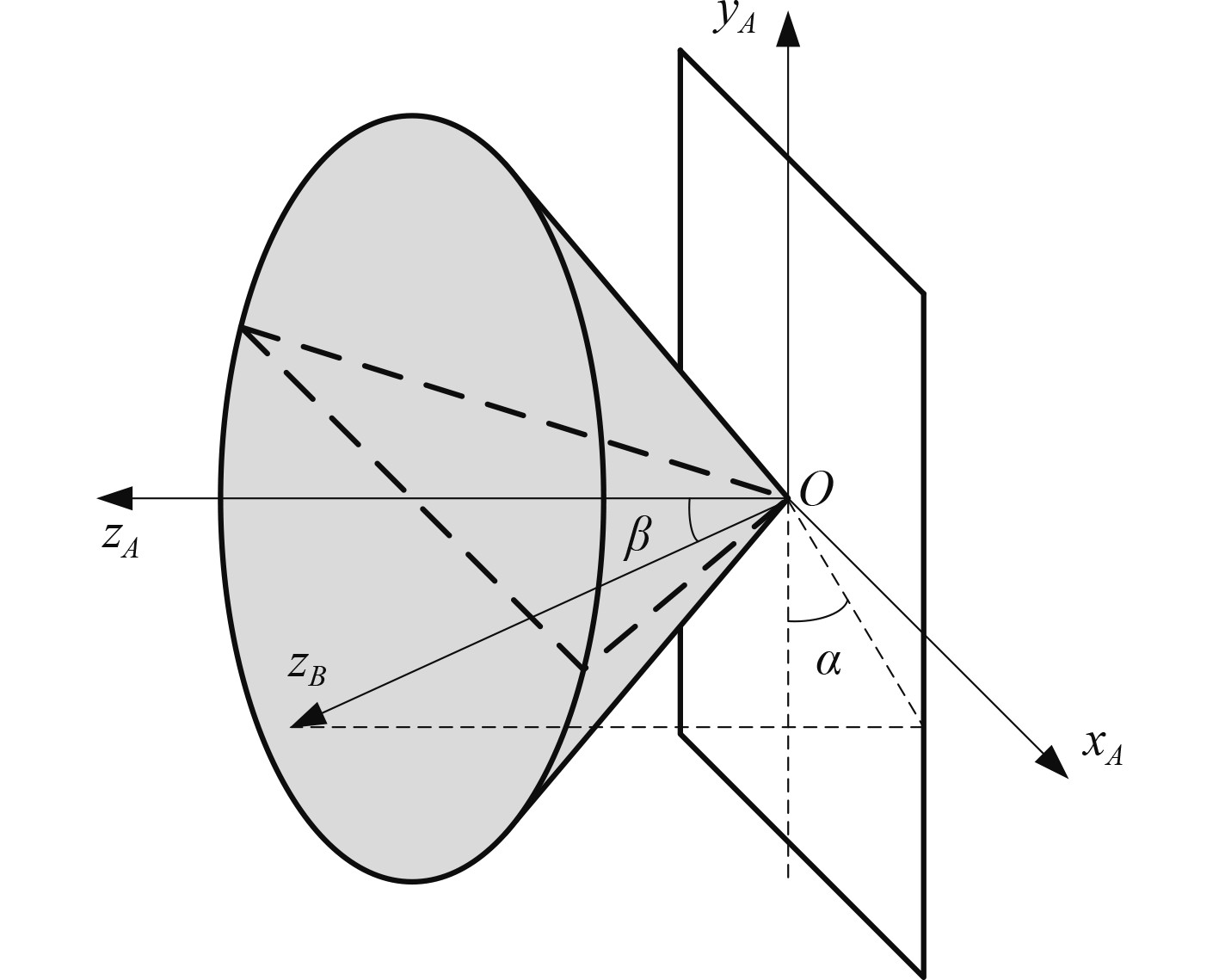
|
图 2 喷口法矢量方向描述 Fig. 2 Description of the normal vector direction of the nozzle |
图中,方位角
| $ {{\boldsymbol{Z}}_B} = {\boldsymbol{R}}({z_B},\alpha ) \cdot {\boldsymbol{R}}({x_B},\beta ) \cdot {\boldsymbol{z}} 。$ | (2) |
式中,
联立式(1)和式(2),可得到多关节串联机构的运动学方程:
| $ {{\boldsymbol{Z}}_B} = \prod\nolimits_{i = 1}^N {{{\boldsymbol{T}}_i}({\theta _i})} \cdot {\boldsymbol{z}} = {\boldsymbol{R}}({z_B},\alpha ) \cdot {\boldsymbol{R}}({x_B},\beta ) \cdot {\boldsymbol{z}} 。$ | (3) |
对于串联机构的关节角度运动学正解,方程组可简记为:
| $ {\boldsymbol{F}}({\boldsymbol{\theta }}) = {[\alpha ,\beta ]^{\text{T}}} ,$ | (4) |
式中,
串联机构关节数量的多少对其运动学正解方法没有影响,均可根据式(1)乘积结果直接解出:
| $ \left\{ \begin{gathered} \alpha = \arcsin ({{{b_1}} \mathord{\left/ {\vphantom {{{b_1}} {\sin \;\beta }}} \right. } {\sin \;\beta }}) ,\hfill \\ \beta = \arccos \;{b_3} 。\hfill \\ \end{gathered} \right. $ | (5) |
当串联机构关节数量大于任务空间的维度数量时,属于冗余自由度机构,存在着无穷多组运动学反解。这类机构在达成给定目标的前提下,可以满足其他附加功能[10]。通过选取合适的约束条件,可以得出希望的关节角控制面。
2 四关节式喷管关节角控制面的求解及分析四关节式喷管的关节自由度为4,具有2个冗余自由度,采用优化算法求得合适的运动学反解。首先确定优化目标与约束条件:
1)矢量推进器喷管的操纵控制,需要根据工作空间内喷口方向的连续变化轨迹,得到对应关节空间中连续变化的角度曲线,通过控制关节角的连续变化,实现喷口偏转角和方位角在任意位置向任意方向的变化。考虑实际操纵过程中各关节运动速度的限制,以相邻位置关节角增量最小为目标,实现关节角局部速度的最小,便于实现关节角的控制。
2)关节转动的驱动设备多为电机或液压马达,均接有供电线缆或液压油路,为防止管线的缠绕,各关节不能进行无限制的连续转动。因此,需要对各关节的旋转角度范围进行约束,避免关节角运动超限。
根据以上优化目标与约束条件,提出一种基于蒙特卡罗模拟法与局部最优目标的运动学反解策略。
2.1 局部最优的运动学反解策略对于此类具有冗余自由度的多关节串联机构,当任意2个关节角度已知,其余关节角度未知情况下,可用Newton迭代法进行运动学反解计算,公式如下:
| $ {\varphi }^{(k\text+1)}={\varphi }^{(k)}-{J}^{-1}\{F({\theta }^{(k)})-{[\alpha ,\beta ]}^{\text{T}}\} 。$ | (6) |
式中:
| $ {\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{{\partial {f_1}({\boldsymbol{\theta }})} \mathord{\left/ {\vphantom {{\partial {f_1}({\boldsymbol{\theta }})} {\partial {\theta _m}}}} \right. } {\partial {\theta _m}}}}&{{{\partial {f_1}({\boldsymbol{\theta }})} \mathord{\left/ {\vphantom {{\partial {f_1}({\boldsymbol{\theta }})} {\partial {\theta _n}}}} \right. } {\partial {\theta _n}}}} \\ {{{\partial {f_2}({\boldsymbol{\theta }})} \mathord{\left/ {\vphantom {{\partial {f_2}({\boldsymbol{\theta }})} {\partial {\theta _m}}}} \right. } {\partial {\theta _m}}}}&{{{\partial {f_2}({\boldsymbol{\theta }})} \mathord{\left/ {\vphantom {{\partial {f_2}({\boldsymbol{\theta }})} {\partial {\theta _n}}}} \right. } {\partial {\theta _n}}}} \end{array}} \right] 。$ | (7) |
式中:
结合上述分析,提出的求解步骤如下:
步骤1 在−170°~170°范围内生成一系列随机角度值组合,每组包含2个随机角度值。
步骤2 将每组角度值随机赋给2个关节作为已知关节角,用Newton迭代法解出其余2个关节角度的所有满足约束条件的反解。
步骤3 从每组角度值产生的所有反解中随机选取一个保存,无解则不保存。
步骤4 计算所有保存反解对应的目标函数值,从中得到一组最优解作为寻解结果。
考虑到各关节角存在的运动范围限制,方位角进行连续转动时,各关节的旋转角度仅在一定范围内摆动。对此采用变目标函数,结合“拟合-寻解”的方式进行计算,具体方法如下:
1)目标取为与方位对称位置的反解关节角度增量最小,保证关节角度的周期摆动。
2)对数据作曲线拟合,以距离拟合曲线最近为目标再次寻解,满足当前轨迹下关节角度变化的连续性。
3)对于不同偏转角下的转动,以相邻偏转角下的反解结果增量最小为目标寻解,对寻解结果再进行步骤2的计算,实现偏转角
针对实际操纵中避免关节角度超限的需求,采用前述 “拟合-寻解”的局部最优方法进行求解。编程计算得出,当四关节型式的最大偏转角度为90°(即关节参数设定为
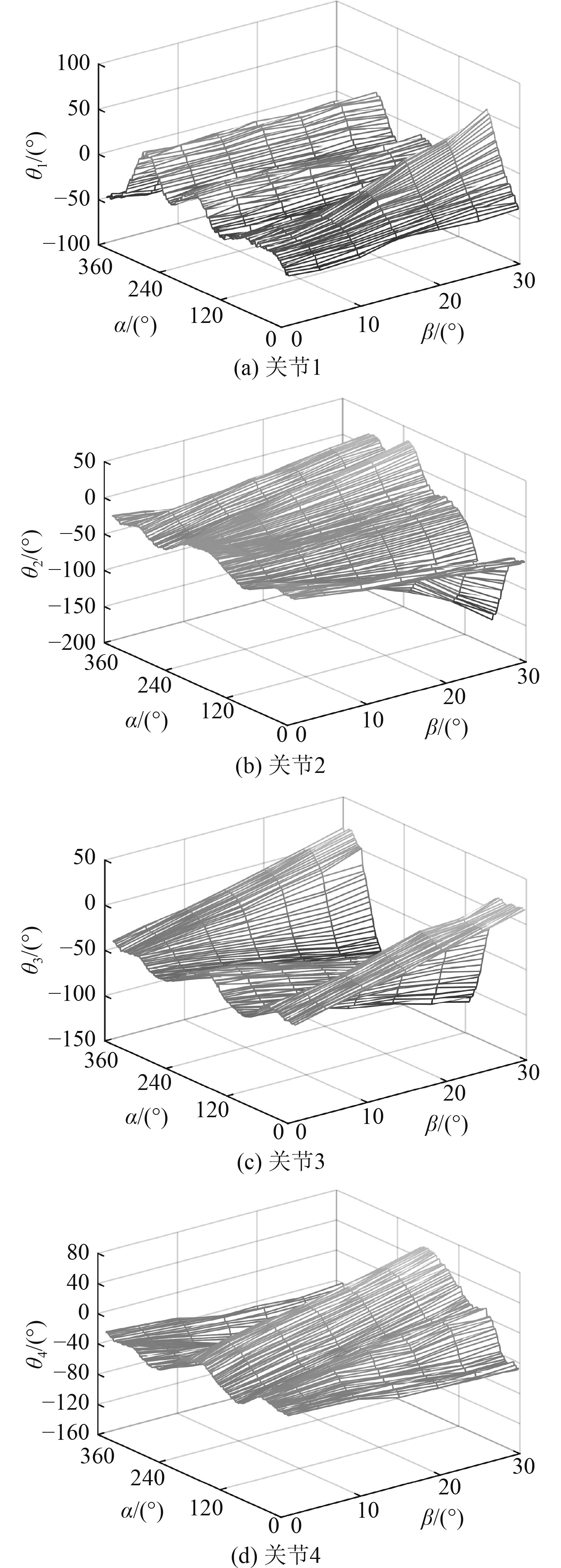
|
图 3 关节角控制面 Fig. 3 Joint angle control surface |
可知,方位角的坐标范围为0~360°,不同偏转角下对应曲线的首尾关节角度值连续,即喷口在按一定偏摆角度进行360°的连续转动时,各关节角仅进行一定范围内的周期性摆动。该图像为连续曲面,其中最大梯度不超过10,各关节可以通过沿对应曲面的连续角度变化实现喷口方向的连续变化,满足控制推力矢量变化的操纵要求。
2.3 控制面效果验证根据所得到的关节角控制面,结合给定的喷口方向运动轨迹,可直接获得对应的关节角变化关系。以喷口的2个典型控制为例,分析对应关节角变化曲线的操纵性。
1)初始位置:
2)初始位置:
根据控制面上对应点,可以得到的各关节角的变化曲线,分别如图4和图5所示。
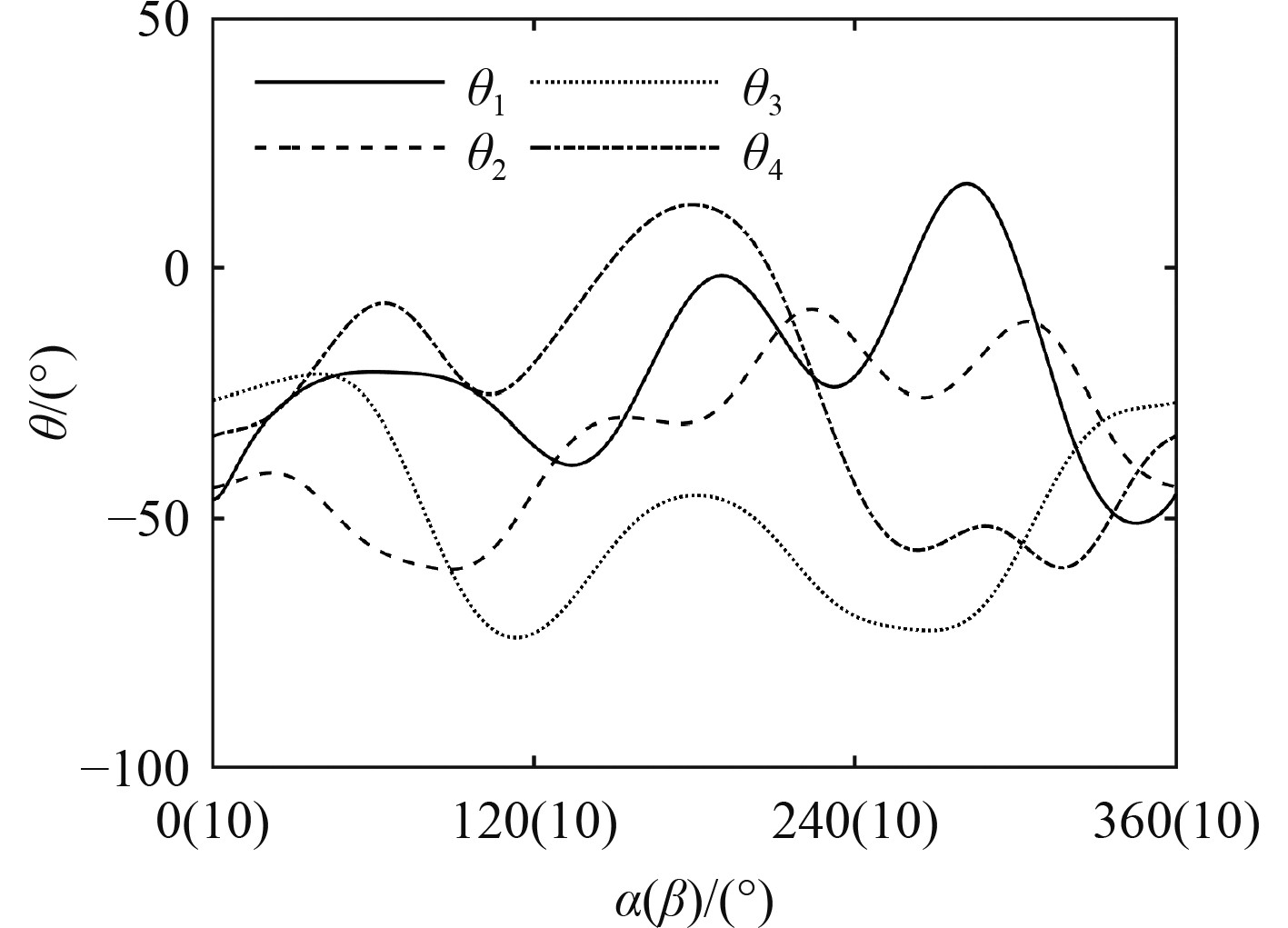
|
图 4 轨迹1关节角对应关系 Fig. 4 Joint angle correspondences for trajectory 1 |
|
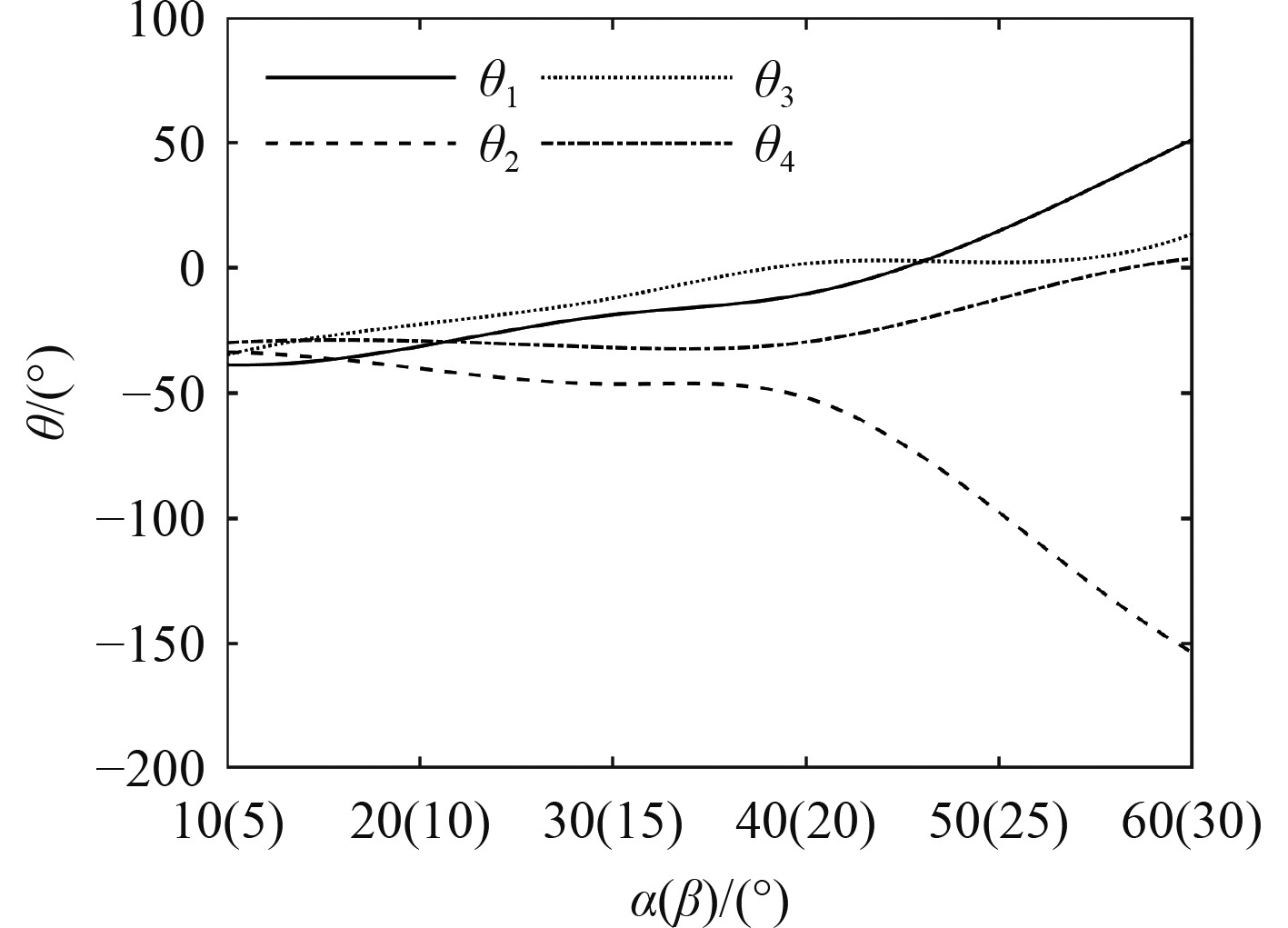
图 5 轨迹2关节角对应关系 Fig. 5 Joint angle correspondences for trajectory 2 |
图4中,在喷口法矢量沿方位角
对于五关节及以上的串联机构型式,显然灵活性更高,但关节数量的增加将导致喷管结构的复杂,使喷管内部的接合面过多,对内部流场产生更为明显的不利影响,不再进行讨论。
3 结 语本文针对应用于大通径矢量喷管设计的多关节串联机构的操纵性,进行机构的运动特性分析,提出了一种基于蒙特卡罗模拟法与局部最优目标的“拟合-寻解”优化算法。以一组关节端面配置参数为
| [1] |
吕雪燕, 罗艳春, 蒋晓莲. 推力矢量技术的应用及影响[J]. 科技资讯, 2012(5): 118. |
| [2] |
张帅, 肖晶晶. 水下矢量推进器研究综述[J]. 舰船科学技术, 2019, 41(7): 5-9. ZHANG Shuai, XIAO Jing-jing. Review of underwater vector propulsion devices[J]. Ship Science and Technology, 2019, 41(7): 5-9. |
| [3] |
徐瀚. 水下机器人矢量推进机构的构型综合与动力学建模[D]. 济南: 山东大学, 2017.
|
| [4] |
李研彪, 徐涛涛, 郑航, 等. 含球面副间隙的空间并联机构动态特性[J]. 浙江大学学报(工学版), 2020, 54(2): 348-356.
|
| [5] |
张雷, 徐海军, 邹腾安, 等. 嵌套Z轴式水下矢量推进系统建模与特性分析[J]. 浙江大学学报(工学版), 2020, 54(3): 450-458+482. ZHANG Lei, XU Hai-jun, ZOU Teng-an, et al.Modeling and property analysis of underwater vector propulsion system based on nested Z-shafts [J]. Journal of Zhejiang University (Engineering Science), 2020, 54(03): 450-458+482. |
| [6] |
方世鹏. 水下矢量推进螺旋桨装置设计与研究[D]. 长沙: 国防科学技术大学, 2008.
|
| [7] |
张凯, 叶金铭. 矢量泵喷推进器水动力性能[J]. 船舶工程, 2019, 41(4): 36-41+144. ZHANG Kai, YE Jin-ming. Hydrodynamic performance of vectorial pump-jet propulsor[J]. Ship Engineering. 2019, 41(04): 36-41+144. |
| [8] |
齐云鹤. 两自由度水下对接转裙研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [9] |
王向阳, 周继红, 刘凯, 等. 三轴承推力矢量喷管运动学建模及试验[J]. 航空学报, 2014, 35(4): 911-920. |
| [10] |
吴鹏, 洪娟, 陈广, 等. 串联冗余自由度机构关节角位置的规划算法[J]. 哈尔滨工程大学学报, 2017, 38(10): 1623-1629,1641. WU Peng, HONG Juan, CHEN Guang, et al. Joints position planning approach for series redundant DOF mechanisms[J]. Journal of Harbin Engineering University, 2017, 38(10): 1623-1629,1641. |
 2022, Vol. 44
2022, Vol. 44

