随着船舶大型化发展趋势,对于船舶波浪载荷的研究由传统的静水弯矩、波浪弯矩到砰击弯矩。波浪弯矩持续作用于船体梁的时间远大于船体梁振动周期,因此,波浪弯矩被视为准静态载荷。目前对船体梁极限承载能力的影响研究主要考虑的输入载荷是波浪弯矩和静水弯矩,关于砰击弯矩对船体梁极限承载能力的影响研究甚少,这与其特定的属性有一定关系。砰击载荷具有幅值大、作用时间短的特点[1]。根据Ochi[2]的理论可知,砰击载荷持续作用于船体梁的时间与船体长度有关,不能将砰击载荷被视为准静态载荷。在极端恶劣的海况下,砰击载荷持续作用的时间虽然很短,但其幅值非常大,对船体梁的极限承载能力有很大的破坏性[3]。基于此,砰击弯矩作用下船体梁动态极限强度研究显得尤为重要。
静力极限强度是目前用于船体结构安全性评估最为广泛的技术手段。砰击载荷作用下船体梁动态响应特性需要考虑船体钢质材料的动态本构关系、惯性效应和应力波效应等,其与静态破坏特性有着明显的差别。目前,船体梁静态极限强度已取得大量研究成果。动态极限强度作为评估船体梁在砰击载荷作用下安全性能的重要指标,对此展开研究的学者很少。因此,对砰击载荷作用下船体梁动态极限强度展开研究显得尤为重要。
本文基于某船的船中部分为对象,在Patran里建立了该船肿部分的有限元模型,并导入Abaqus软件中进行数值仿真计算。基于动力显示方法获得静态载荷作用下船体梁弯矩-转角曲线、静态极限强度(Mu)和静态极限转角(Ry0),将静态极限转角作为评估砰击动载荷作用下船体梁动态极限强度的基准。系统研究了砰击载荷持续时间、砰击冲量和砰击载荷幅值对船体梁动态响应特性的影响。
1 有限元模型 1.1 材料模型船体结构钢质材料在动态砰击载荷作用下的材料特性不同与静态载荷作用下的材料特性,其本构关系不同。采用Cowper-Symonds公式模拟材料动态本构模型[4]:
| $ {\sigma _{{{dy}}}} = {\sigma _y}\left( {1 + {{\left( {\frac{{\dot \varepsilon }}{D}} \right)}^{1/q}}} \right)。$ |
式中:
船体舱段结构由2层甲板、单底和舷侧组成,舱段总长为3.4 m,总宽约为3.26 m,型深约为2.4 m。图1为舱段结构图。x轴沿船长方向,指向首部为正;y轴沿船宽方向,指向左舷为正;z轴沿型深方向,向上为正。

|
图 1 舱段结构图 Fig. 1 Cabin structure diagram |
模型两端建立相应的独立点,采用多点约束进行边界条件的定义,边界条件为一端释放y向转角和x向位移,另一端释放y向转角,其他方向固定。根据此边界条件,在两端分别施加载荷,由于本船静水中为中垂状态,在波浪中航行时,其中垂状态较为危险,因此施加载荷使其产生中垂状态,研究该状态下的动态极限强度。具体的边界约束情况见表1。
|
|
表 1 边界条件 Tab.1 Boundary conditions |
为了研究船体梁动态破坏特性,需要先计算模型的静态极限强度。图2给出了船体梁静态极限强度数值仿真弯矩-转角曲线,可以看出:当弯矩达到极限前,弯矩曲率基本为线性状态,当舱段的极限弯矩达到3.35×1010 N·mm时,转角为0.0046 rad(极限状态);随着转角的增大,弯矩下降。

|
图 2 船体梁静态弯矩-转角曲线 Fig. 2 Hull girder static bending moment-rotation curve |
图3和图4给出了01甲板和1甲板的应力云图和塑性应变云图。通过图3可以看出:当载荷达到极限状态时,01甲板的边板、开口边板(船中)和舷侧列板已经发生塑性变形,达到了屈服极限;当载荷作用结束后,01甲板的边板、开口边板(船中)和舷侧列板已经发生了失效变形。通过图4可以看出:极限状态下1甲板开口角隅区域、开口边板(船中)发生了局部屈服;当载荷作用结束后,1甲板的边板、开口边板(船中)和舷侧列板也已经发生了失效变形。

|
图 3 01甲板应力云图和塑性应变云图 Fig. 3 01 Deck stress cloud chart and plastic strain cloud chart |

|
图 4 1甲板应力云图和塑性应变云图 Fig. 4 1 Deck stress cloud chart and plastic strain cloud chart |
将砰击弯矩简化为由半正弦波形状函数的

|
图 5 砰击弯矩历程曲线 Fig. 5 Slamming moment history curve |
| $ f(t) = \sin \left(\frac{{{\text{π}} t}}{{{t_p}}}\right),$ |
| $ {M_k}\left( t \right) = {M_{\max }}f(t) = {M_{\max }}\sin \left(\frac{{{\text{π}} t}}{{{t_p}}}\right) 。$ |
船舶在航行过程中产生的颤振周期范围为0.5 ~2 s[8]。船体梁在波浪中作用时会产生作用时间短、载荷幅值高的砰击载荷,其持续作用时间通常具有毫秒量级[9]。砰击弯矩作用下船体梁动态破坏特性分析工况如表2所示。L01~L06为不同砰击持续作用时间;L03,L07~L10为不同砰击载荷幅值;L03,L11~L14为不同砰击载荷冲量。
|
|
表 2 砰击弯矩作用下船体梁动态破坏特性分析工况 Tab.2 Analysis of dynamic failure characteristics of hull girder under slamming bending moment |
图6和图7给出了船体梁在工况L03下01甲板和1甲板的应力云图和塑性应变云图。由图6可知,L03工况下船体梁的最大转角为0.004852 rad;01甲板的边板、开口边板(船中)和舷侧列板发生了塑性变形,达到了屈服极限;当载荷作用结束后,01甲板的边板、开口边板(船中)和舷侧列板发生了塑性变形,但没有发生失效变形。通过图7可以看出:1甲板开口角隅区域、开口边板(船中)发生了局部屈服;当载荷作用结束后,仅有1甲板的开口边板(船中)产生了塑性变形,未发生失效变形。

|
图 6 01甲板应力云图和塑性应变云图 Fig. 6 01 Deck stress cloud chart and plastic strain cloud chart |

|
图 7 1甲板应力云图和塑性应变云图 Fig. 7 1 Deck stress cloud chart and plastic strain cloud chart |
将砰击弯矩下船体梁动态响应特性与静态极限强度对比可知:静态极限状态下整个模型发生了失效变形,但砰击动载作用下整个模型仅有01甲板的边板、开口边板(船中)和舷侧列板发生了塑性变形,整个模型并未发生失效破坏。由此可见,砰击弯矩下船体梁动态失效模式与静态失效模式有所不同,动态载荷作用下的结构响应(Ry0)峰值更大,且结构并未发生失效变形,在局部开口区域(强度较弱)发生了较大的塑性应变。
L03,L04和L05工况下船体梁动态响应曲线如图8所示。可知:船体梁端面转角在砰击载荷峰值之后达到最大值,在时间维度有滞后性;当砰击弯矩衰减为0时,船体梁端面有残余转角产生(小于静态极限转角Ry0);L03工况下船体梁的响应峰值大于L04和L05工况下的响应峰值,L04和L05工况作用下的船体梁响应峰值与静态载荷作用下的响应峰值(Ry0)非常接近,这是因为L03工况下的砰击时间最为接近船体梁的固有振动周期(T=8.7 ms),可能激发了共振,导致响应峰值结果增大;根据Cui[10]的结论,可知L04和L05工况作用下船体梁结构响应过程可被看成准静态响应。

|
图 8 无量纲端面转角时间历程曲线 Fig. 8 Time history curve of dimensionless end face angle |
表3给出了砰击弯矩作用下船体梁的响应峰值和残余转角。可知,L11工况作用下对应的响应峰值结果最大。这是因为L11的砰击持续时间与船体梁的固有振动周期最接近,且砰击弯矩幅值最大。由于残余变形对船体梁剩余极限强度有着很大的影响,因此,深入研究砰击载荷的持续作用时间、载荷幅值和砰击冲量对船体梁残余变形的影响显得尤为重要。
|
|
表 3 无量纲动态响应峰值和残余转角 Tab.3 Dimensionless dynamic response peak value and residual turning angle |
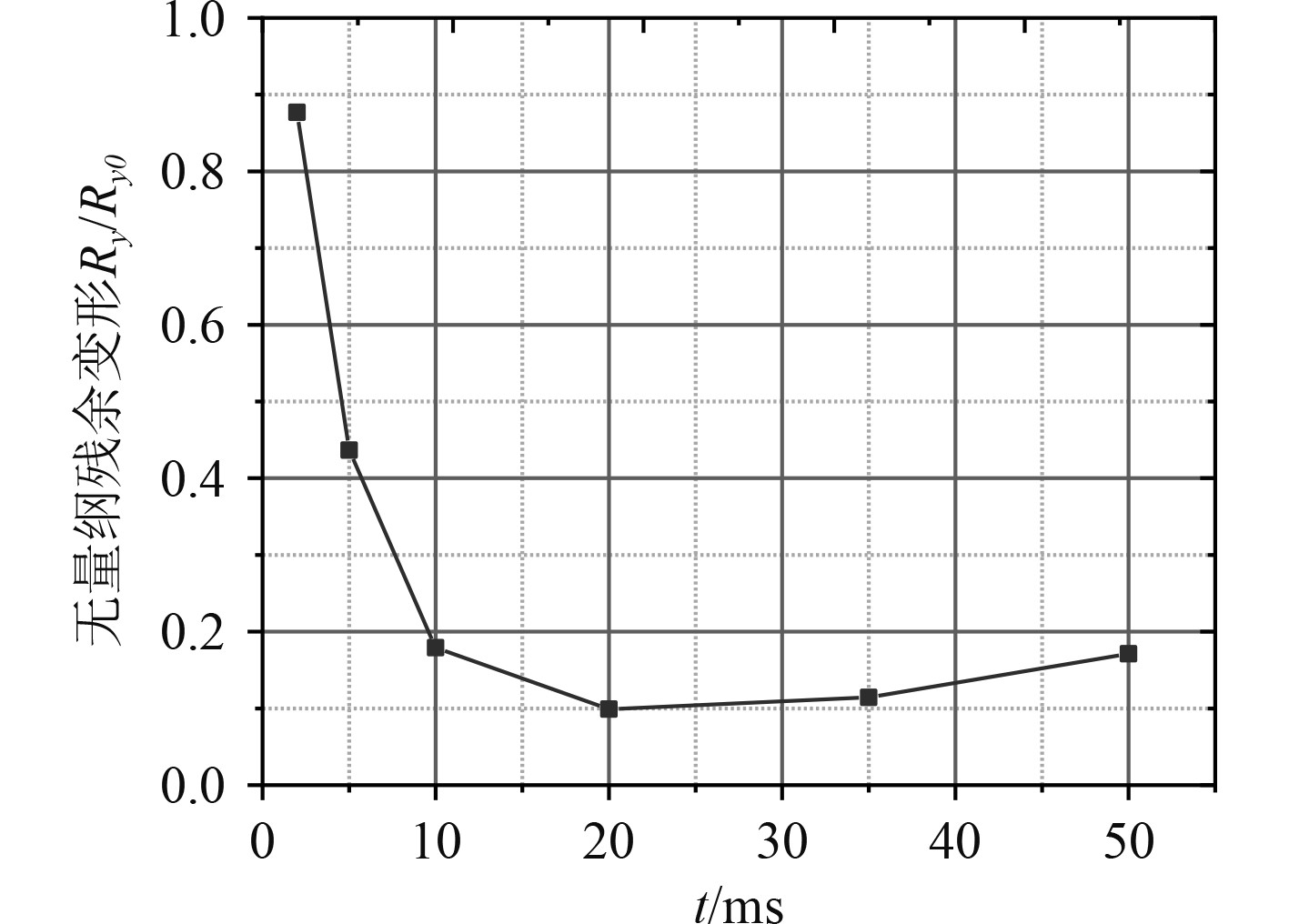
根据计算工况表2可知:L01~L06工况作用下的载荷幅值相同,砰击时间不同。由图9可得,当tp=2 ms时,无量纲残余变形最大;当tp ≥10 ms 时,无量纲残余变形较小,随着砰击时间的增大残余变形变化很小。由此可得:当砰击时间在2~10 ms时,砰击时间对船体梁动态响应的影响非常敏感;当砰击时间tp ≥10 ms时,砰击时间对船体梁动态响应的影响很小,可视为准静态响应过程。
|
图 9 无量纲残余变形-砰击持续时间曲线 Fig. 9 Dimensionless residual deformation-slamming duration curve |
根据计算工况表2可知,L03,L11~L14工况作用下的砰击冲量相同,砰击时间和砰击弯矩不同。由图10可知,砰击冲量一定时,随着砰击持续时间的减小,船体梁端面动态响应峰值和残余变形增大。结合砰击载荷持续时间对船体残余变形的影响分析可知,砰击载荷一定时,砰击持续时间越长,其对应的砰击冲量越大,但相应的无量纲残余变形却越来越小,即船体梁残余变形对砰击载荷持续时间非常敏感。

|
图 10 砰击冲量一定时船体梁端面无量纲残余变形随砰击时间的变化曲线 Fig. 10 Dimensionless residual deformation of hull girder-slamming duration curve when the slamming impulse remains unchanged |
根据计算工况表2可知,L03,L07~L10工况作用下的砰击时间相同,砰击弯矩不同。由图11可知,砰击时间一定时,船体梁端面动态响应峰值和残余变形随砰击弯矩幅值的增大而增大。L07工况作用下船体梁动态响应峰值和残余变形远大于静态响应对应的结果。

|
图 11 无量纲残余变形-无量纲砰击弯矩曲线 Fig. 11 Dimensionless residual deformation-dimensionless slamming bending moment curve |
结合图12所示5种工况L03和L07~L10下模型塑性应变云图可得:当Mmax/M0>10/9时,船体梁在砰击弯矩作用下会产生局部屈曲和屈服,随着砰击弯矩的增加,其残余变形迅速增大。根据B-H准则[11]的定义,此时的砰击弯矩可定义为船体梁的动态极限强度。

|
图 12 5种工况L03和L07~L10下模型塑性应变云图 Fig. 12 Plastic strain cloud diagram of the model under L03 and L07~L10 conditions |
本文基于数值仿真方法研究砰击载荷作用下船体梁的动态响应特性,得到如下结论:
1)砰击弯矩下船体梁动态失效模式与静态失效模式不同,动态载荷作用下的结构响应(Ry0)峰值更大;
2)砰击弯矩一定时,砰击持续时间越长,其对应的砰击冲量越大,但相应的无量纲残余变形却越来越小,即船体梁残余变形对砰击载荷持续时间非常敏感;
3)砰击冲量一定时,随着砰击持续时间的减小,船体梁端面动态响应峰值和残余变形增大;
4)砰击时间一定时,船体梁端面动态响应峰值和残余变形随砰击弯矩幅值的增大而增大。
| [1] |
XU M C, SOARES C G. Comparisons of calculations with experiments on the ultimate strength of wide stiffened panels[J]. Marine structures, 2013, 31: 82-101. DOI:10.1016/j.marstruc.2013.01.003 |
| [2] |
OCHI MK, MOTTER LE. Prediction of slamming characteristics and hull response forship design[J]. Transactions SNAME 1973, 81: 144−176.
|
| [3] |
CLAUSS G F, KAUFFELDT A, KLEIN M. Systematic investigation of loads and motions of a bulk carrier in extreme seas[C]//ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2009: 277−287.
|
| [4] |
杨斌. 砰击载荷作用下集装箱船船体结构动态响应和极限强度研究[D]. 上海: 上海交通大学, 2019.
|
| [5] |
PAIK J K. Practical techniques for finite element modeling to simulate structural crashworthiness in ship collisions and grounding (Part I: Theory) [J]. Ships and Offshore Structures 2007; 2(1): 69-80.
|
| [6] |
PAIK J K. Ultimate limit state analysis and design of plated structures[M]. John Wiley Sons, 2018.
|
| [7] |
IIJIMA K, SUZAKI Y, FUJIKUBO M. Scaled model tests for the post-ultimate strength collapse behavior of a ship's hull girder under whipping loads[J]. Ships and Offshore Structures, 2015, 10(1): 31-38. DOI:10.1080/17445302.2013.870774 |
| [8] |
American Bureau of Shipping. Guide for Slamming Loads and Strength Assessment for Vessels[S]. American Bureau of Shipping, 2011.
|
| [9] |
ZHANG N, ZONG Z. The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble[J]. Journal of Fluids & Structures, 2011, 27(8): 1326-1336. |
| [10] |
CUI S, HAO H, CHEONG H K. Numerical analysis of dynamic buckling of rectangular plates subjected to intermediate-velocity impact[J]. International Journal of Impact Engineering, 2001, 25(2): 147-167. DOI:10.1016/S0734-743X(00)00035-X |
| [11] |
BUDIANSKY B. Axisymmetric dynamic buckling of clamped shallow spherical shells[J]. NASA TN, 1962, 1510: 597-606. |
 2022, Vol. 44
2022, Vol. 44
