2. 华中科技大学,湖北 武汉 430074;
3. 上海华为技术有限公司,上海 201206
2. Huazhong University of Science and Technology, Wuhan 430074, China;
3. Shanghai Huawei Technology Co. Ltd., Shanghai 201206, China
复合材料轻质、高强度及其优质的减振效果,在潜艇浮筏结构有着巨大的应用前景。牟文珺[1]在复合材料基座对于船舶设备振动传递的控制方法研究中,进行模态分析和设备振动传递分析。
Gibson等[2]通过测量增强复合材料结构模态振动响应以测量其结构和材料特性。研究表明,测试单个振动模式或多个振动模式下的模态可确定复合材料结构的阻尼因子和弹性模量。H Abramoich等[3]利用磁滞回线法研究Hexply 8552 AGP 280-5H制成的复合层压板的阻尼特性,并与铝制样品结果对比。结果表明,磁滞回线法测得结构损耗因子与激励频率线性相关,与预载荷和应力大小无关。Hong[4]团队提出一种利用高频材料阻尼统计,对模态阻尼进行数值计算以及改进瑞丽阻尼概念的方法来预测复合材料的结构阻尼。Vescoini等[5]利用动态力学试验测试层压板试样的阻尼特性。郭万涛等[6]通过对复合材料基座和钢结构基座进行模态测试和频响测试,分析比较其减振性能。
纤维复合材料采用有限元软件进行仿真计算时,难点在于结构阻尼的描述。洪明等[7]利用动力特性试验测量复合板材的固有频率、模态阻尼和幅频响应特性,在共振时,根据自由衰减曲线或动力放大系数确定板材阻尼。Bhudolia[8]以碳纤维作为增强材料,Elium树脂为基体材料的热塑性管状复合材料,并对其进行低速冲击、弯曲和振动试验,将结果与碳纤维环氧树脂复合材料进行对比分析。
桁架式浮筏以轻质可靠、隔振性能优越的特性逐渐得到各国舰船工程师的重视[9]。此外,桁架式浮筏可设计性较高[10],各设计成周期单元,利用周期特性提高浮筏的减振降噪特性[11]。况成玉等[12]运用有限元法和频响函数综合法建立周期桁架浮筏系统的振动传递模型,研究表明周期桁架浮筏隔振性能更为有效。本文在周期桁架浮筏基础上将复合材料应用于桁架浮筏,测试其减振特性。
1 管件频响试验本文主要测试钢制圆管和复合材料管以及添加阻尼振子后,管件的固有频率和阻尼比的变化规律。钢管和复合材料管均为一端固定约束的悬臂形式,采用锤击法和加速度传感器记录其激励和响应数据,并计算其频响函数,进而求解固有频率和阻尼比。
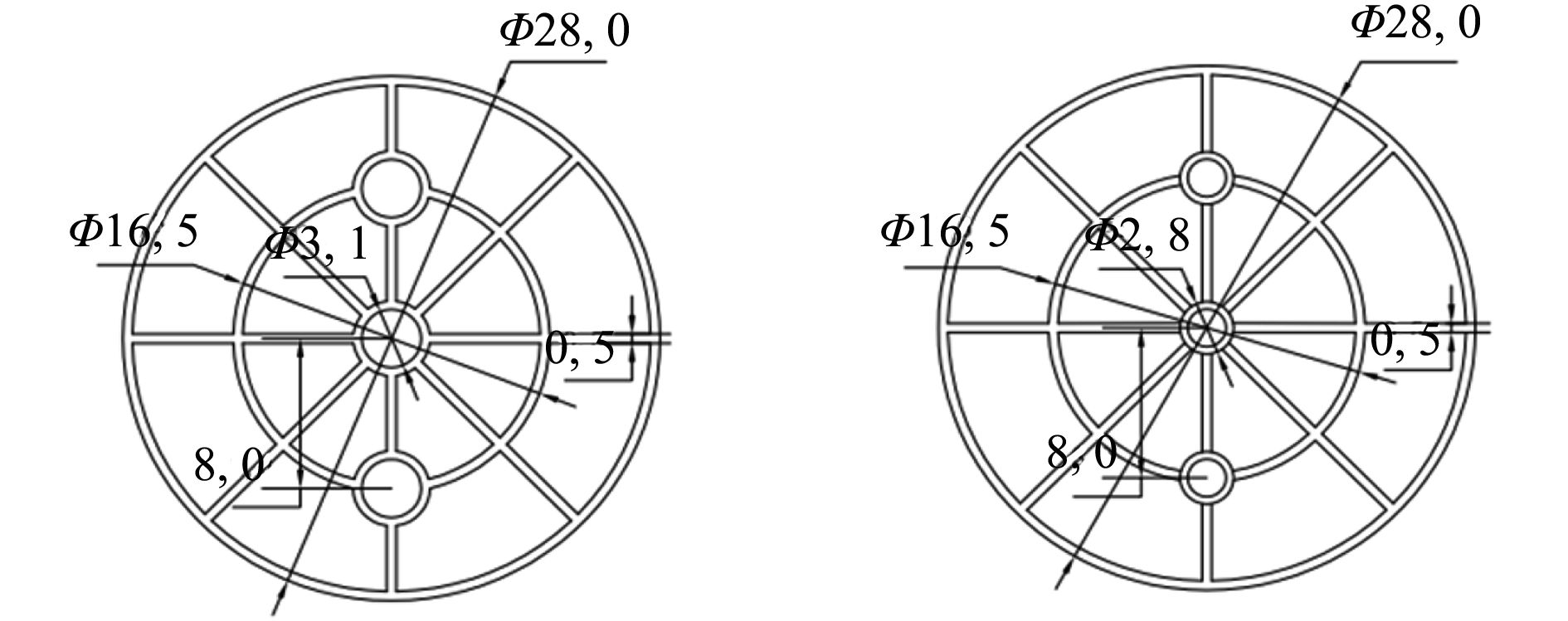
1.1 阻尼振子设计阻尼振子的结构形式设计对于研究阻尼块对于管件固有频率和阻尼比的影响至关重要。在设计阻尼振子时,一方面要求阻尼振子需要一定的结构强度,能够承受阻尼沙的振动冲击;另一方面,要求阻尼沙与阻尼振子之间的接触面积尽可能的大,通过阻尼沙粒之间的不断碰撞和摩擦达到阻尼沙减振降噪的目的,具体设计如图1所示。
|
图 1 阻尼块设计图 Fig. 1 Design drawing of damping block |
通过3D打印完成阻尼振子的制作,其材料为ABS,规格为1.75±0.02 mm。试验采用的阻尼沙为纯白石英砂,其二氧化硅纯度在99.5%以上,硬度为7.5,规格为0.1~0.2 mm,70~120目。

|
图 2 阻尼块三维图 Fig. 2 Three dimensional drawing of damping block |
在凸台部分填充阻尼沙,平台部分提供振动空间,凸台部分连接对应的小孔,起定位和固定作用,保证填充阻尼沙的扇形区域与提供振动的区域一一对应,这也是为使结构在受到激励时,阻尼沙能够充分地消耗能量,从而达到减振的效果。
1.2 频响试验试验的主要目的是探究装沙比例对管件阻尼比的影响,为保证约束条件的一致,管件均采用悬臂结构。本次试验购买的钢管和复合材料管长度均为1 000 mm,其中900 mm为试验悬臂部分,剩余100 mm用作支座固定。复合材料的密度为1.56 t/m3,其等效杨氏模量约为200 GPa。
管件阻尼比测试试验台架如图3所示,钢管或复合材料管利用支座完全固定在一工字钢上。在其悬臂末端利用3D打印一圆弧平台,在其上粘接一带有螺纹的水晶支座,加速度传感器通过螺纹固定在悬臂末端,测试其垂向加速度响应。

|
图 3 频响试验台架 Fig. 3 Frequency response test bench |
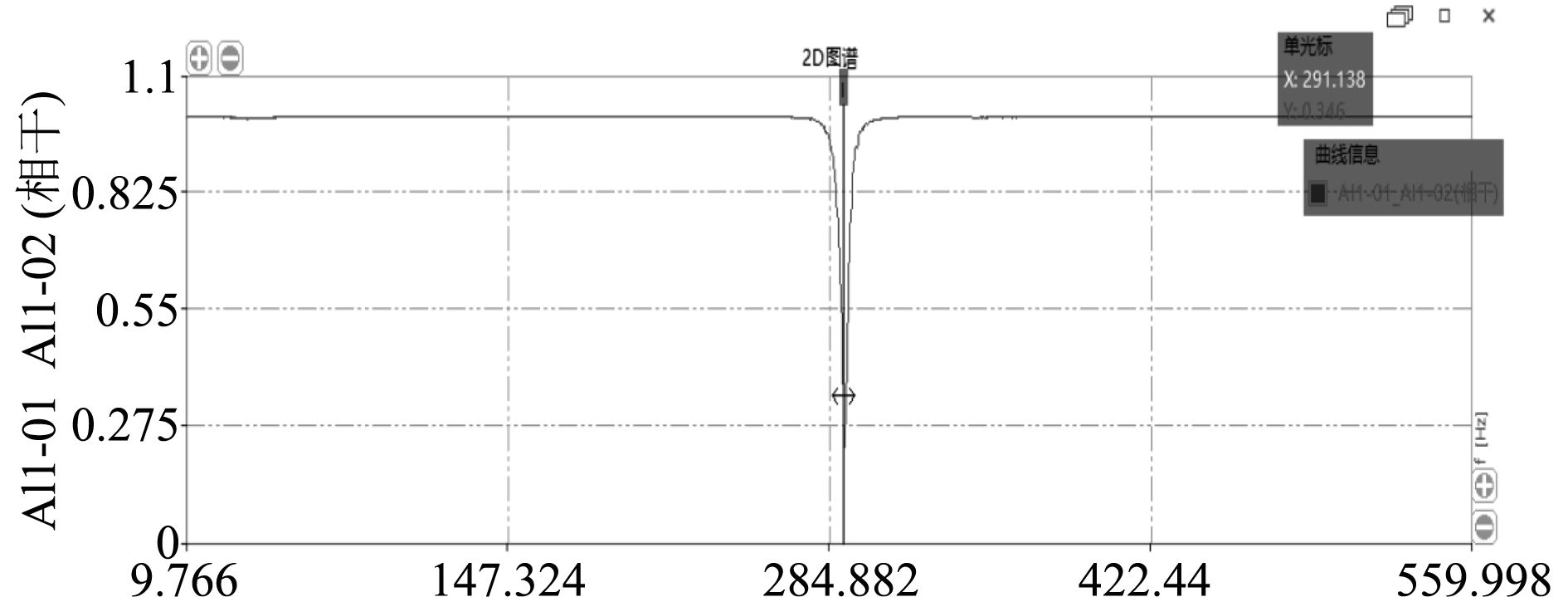
本次频响试验采用锤击法,力信号与响应信号的相干性应当在可控范围内。如图4所示,加速度衰减信号与力信号的相干始终在1附近,表明试验条件较为良好,数据可靠。由相干曲线与频响曲线对比可知,在频率为292 Hz附近,出现结构的反共振点,相干性也降至零点附近。
|
图 4 相干曲线 Fig. 4 Coherence curve |
测定的加速度信号与力信号的比值即结构的频响函数,根据频响函数可得到结构的前3阶固有频率分别为32.65 Hz,205.69 Hz,552.67 Hz。由于结构的振动特性主要由前几阶固有频率,特别是第1阶固有频率决定,因此本次试验只测定第1阶固有频率的阻尼比。根据其幅频曲线由半功率点法,求得钢制管件的阻尼比值为0.007 4。

|
图 5 钢制管件自由衰减曲线 Fig. 5 Free attenuation curve of steel pipe |

|
图 6 钢制管件频响曲线 Fig. 6 Frequency response curve of steel pipe fittings |
对钢管进行仿真并将仿真结果与频响试验结果进行对比,结果如表1所示,误差均在允许范围内。
|
|
表 1 钢制管件固有频率 Tab.1 Natural frequency of composite tube |
为测定复合材料碳纤维管的阻尼比,在悬臂末端通过加速度传感器采集响应数据,在距离末端300 mm位置处使用力锤进行激励。
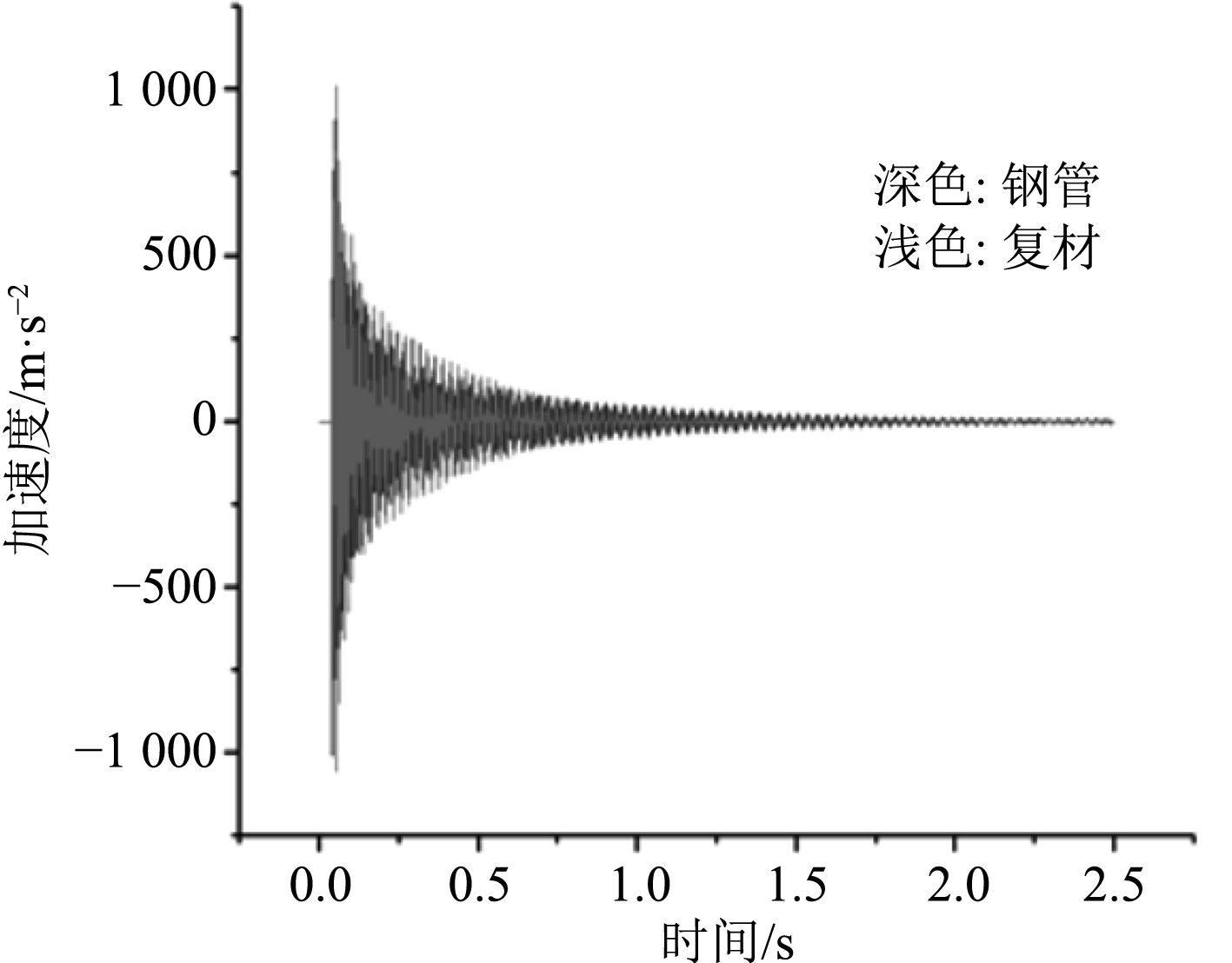
如图7所示,力锤每次激励的值不同,其管的响应也不尽相同,在激励开始后0.5 s的时间范围内,复合材料管的激励响应远远大于钢管。纯碳纤维管受力锤激励反复振动持续大约1.5 s,较钢管衰减时间缩短大约0.5 s。
|
图 7 复合材料管及钢管自由衰减曲线 Fig. 7 Free attenuation curve of composite pipe and steel pipe |
|
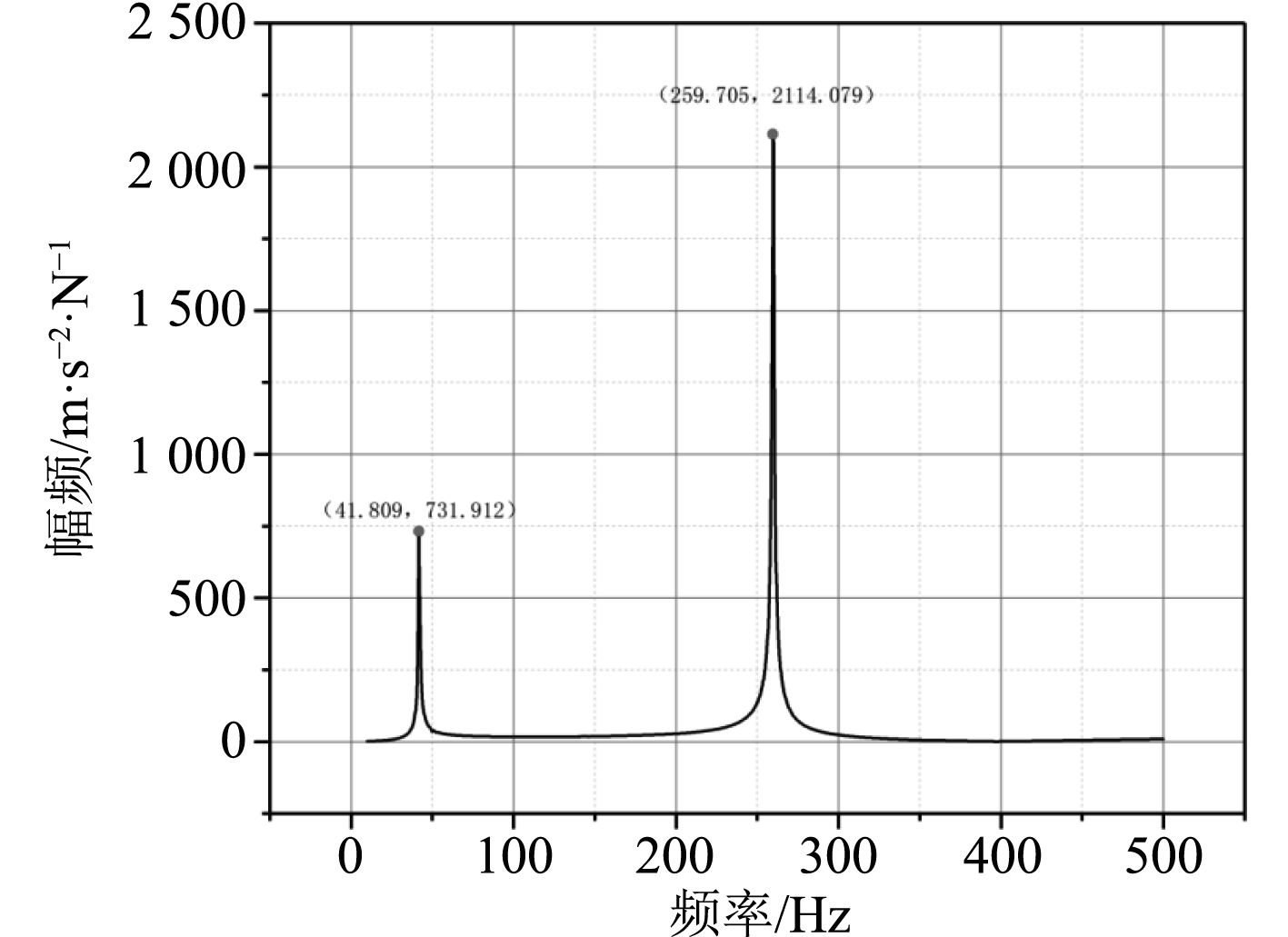
图 8 复合材料管频响曲线 Fig. 8 Frequency response curve of composite tube |
根据测得的复合材料空管的自由衰减加速度信号,以及其力信号,得到其频响曲线。试验测试结果表明其1阶固有频率为41.81 Hz,2阶固有频率为259.71 Hz,且在频率397.34 Hz处,结构存在反共振点,继而根据频响函数求解其阻尼比为0.010 4。由此可知复合材料在结构减振设计领域有着广泛的应用前景。
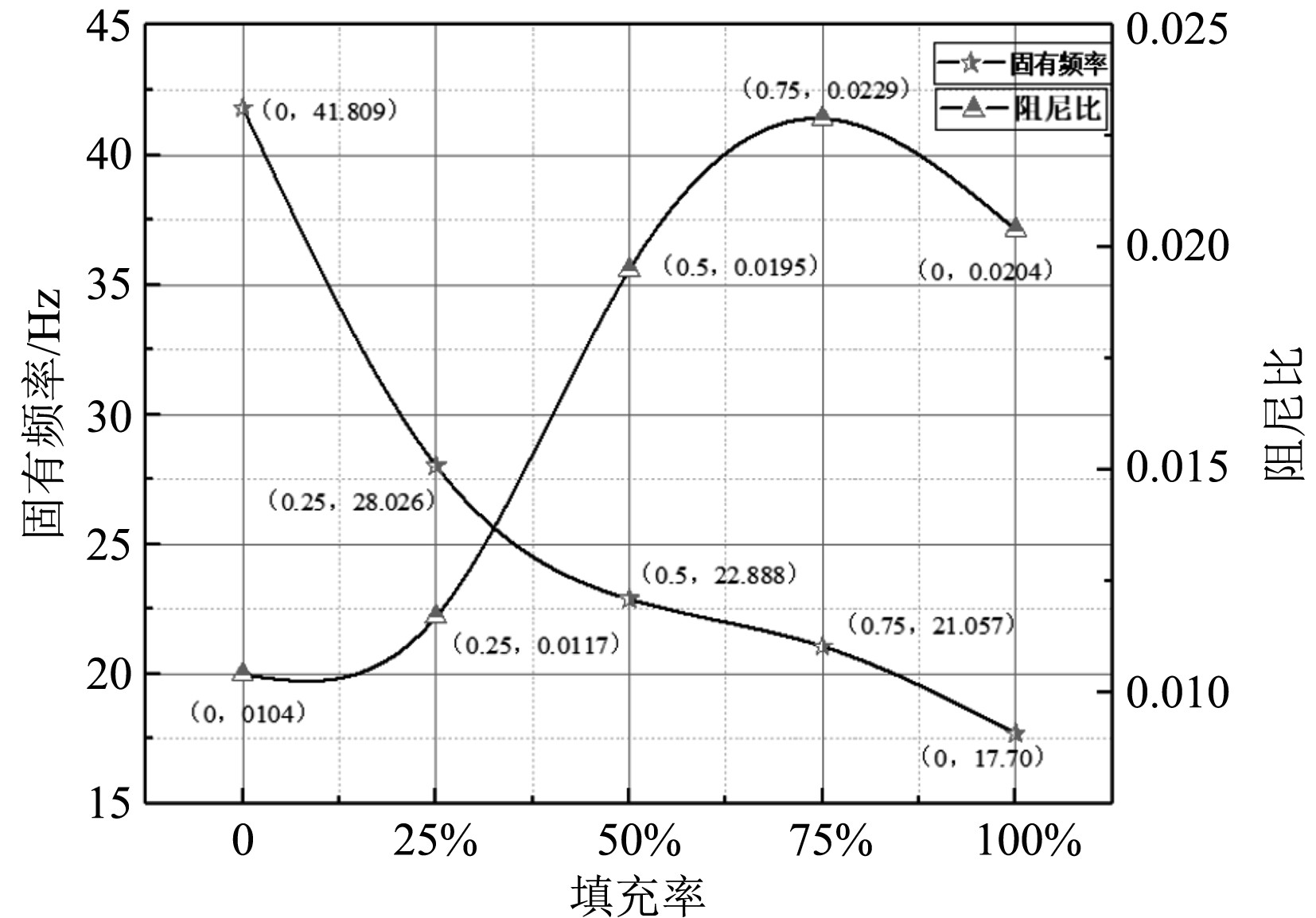
2.3 复材管件阻尼块试验为探究装填不同比例阻尼沙的阻尼块对管件阻尼比的影响,设计填充率分别为25%,50%,75%,100%阻尼块。
将四周表面涂有AB胶的阻尼振子塞入复合材料管内,待自然晾干完全固定后测试管件动态响应特性。填充完成后,管件利用支座刚性固定在基座上,利用加速度传感器记录其响应数据。
实验结果如图9所示,随着阻尼块中阻尼沙填充率的增加,其材料阻尼比也随之增加,在填充率75%左右达到峰值0.022 9,其管件固有频率也逐渐降低。
|
图 9 不同填充率下管件振动特性比较 Fig. 9 Comparison of vibration characteristics of pipe fittings with different filling ratios |
本次试验采用的3k碳纤维为各向同性材料,密度为1.56 kg/m3,杨氏模量为115 GPa。环氧树脂为各向异性材料,其材料参数如表2所示。试验所用复合管,最外2层为3k碳纤维,内层为环氧树脂,共有9层单向层。沿管长方向前4层铺层角度分别为0°,90°,0°,90°,后5层铺层角度均为90°。
|
|
表 2 碳纤维/环氧树脂材料参数表 Tab.2 Carbon fiber / epoxy material parameter table |
Abaqus中对复合材料分析单元主要有分层壳单元、分层实体单元以及实体壳单元3类,实体壳单元分析响应与壳单元相似,与纯粹的壳单元和实体单元相比,在复合材料层合结构厚度方向的响应更加准确。
采用拉伸壳,复合材料单层板建立三维模型。悬臂约束管件端部,运用S4R四结点壳单元划分网格,基本网格大小设定为4 mm,求解碳纤维复合材料管件的前2阶固有频率,将仿真结果同试验结果进行对比,如表3所示。
|
|
表 3 复材管固有频率 Tab.3 Natural frequency of composite tube |
与碳纤维复合材料管频响试验测试相比,1阶固有频率误差为4.52%,2阶固有频率误差为3.48%,均不超过5%,考虑试验约束条件和传感器支座等因素影响,利用Abaqus层合板壳建模分析的结果与试验结果吻合。
4 桁架浮筏优化 4.1 钢制桁架浮筏仿真鉴于桁架式浮筏轻便和突出的减振能力,本文先对相同尺寸下常见的矩形式桁架浮筏、三角式桁架浮筏、错位式桁架浮筏,分析其静载强度和结构减振性能,选取最优的结构形式对其优化。
对以上3种方案进行仿真分析,在桁架顶部中间施加5 000 N的集中载荷以及施加整体载荷,舱段两端采用简支约束,并对3种方案进行对比结果如表4所示。
|
|
表 4 各方案静动态特性比较 Tab.4 Comparison of static and dynamic characteristics of each scheme |
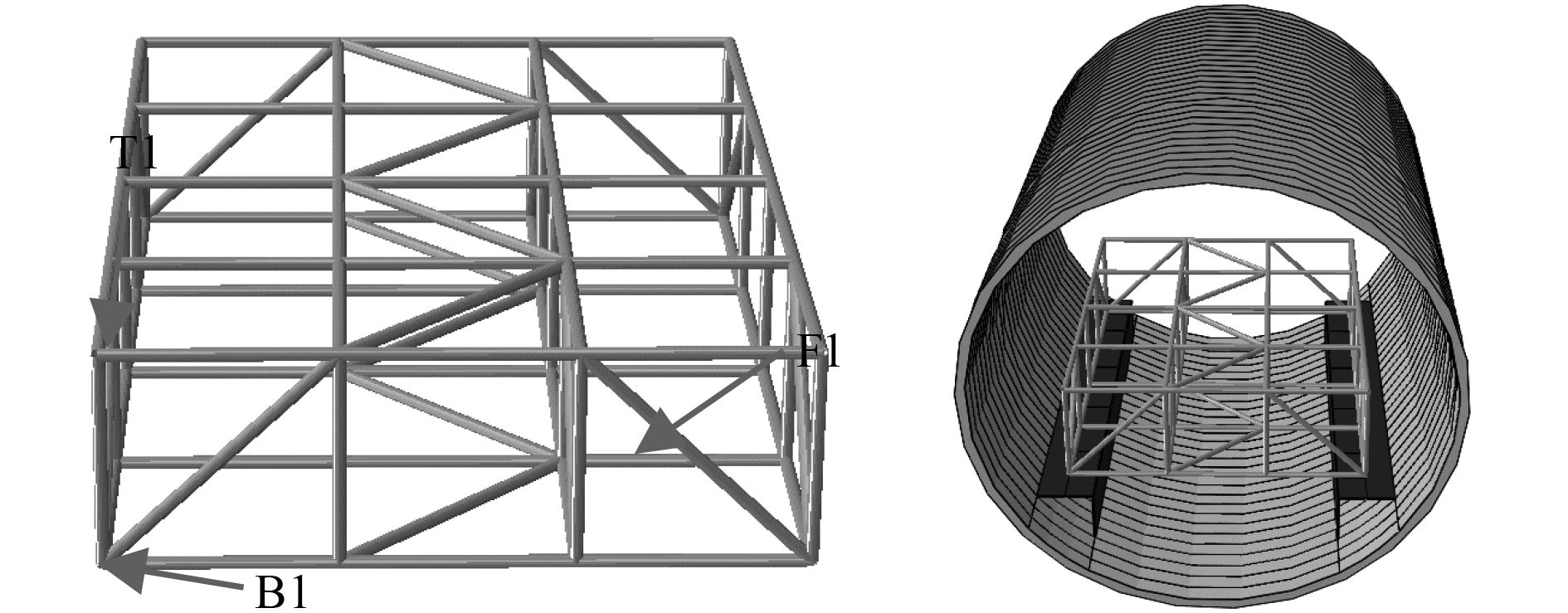
可知,矩形桁架式浮筏隔振性能优越,因此在此基础上对矩形桁架浮筏结构进行优化。在保证桁架安装基座和舱段壳体结构不变的情况下,对桁架浮筏结构优化如图10所示。
|
图 10 优化桁架浮筏示意图 Fig. 10 Schematic diagram of optimized truss floating raft |
|
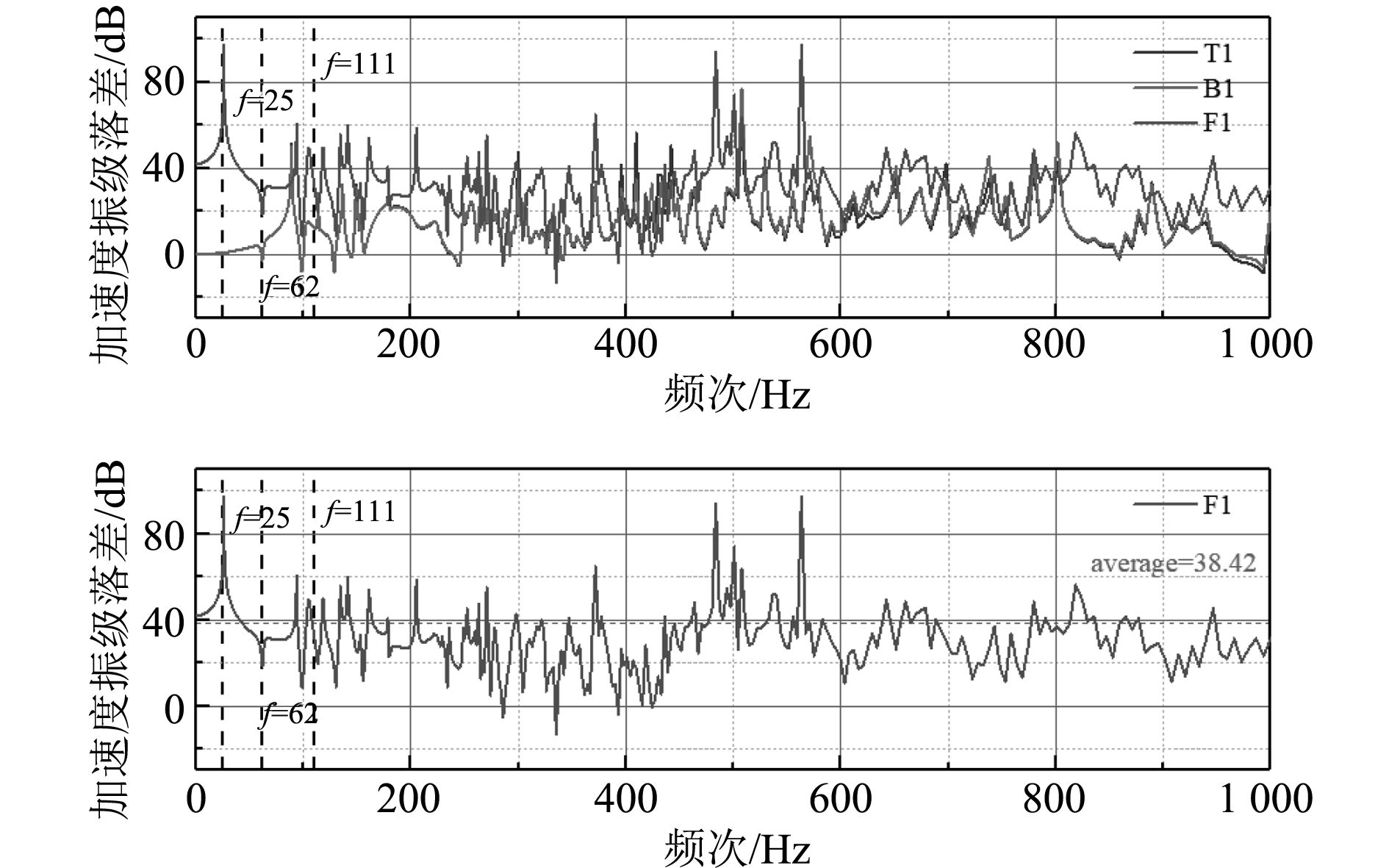
图 11 优化桁架浮筏各点加速度振级落差 Fig. 11 Acceleration vibration level difference of each point of the truss optimization floating raft |
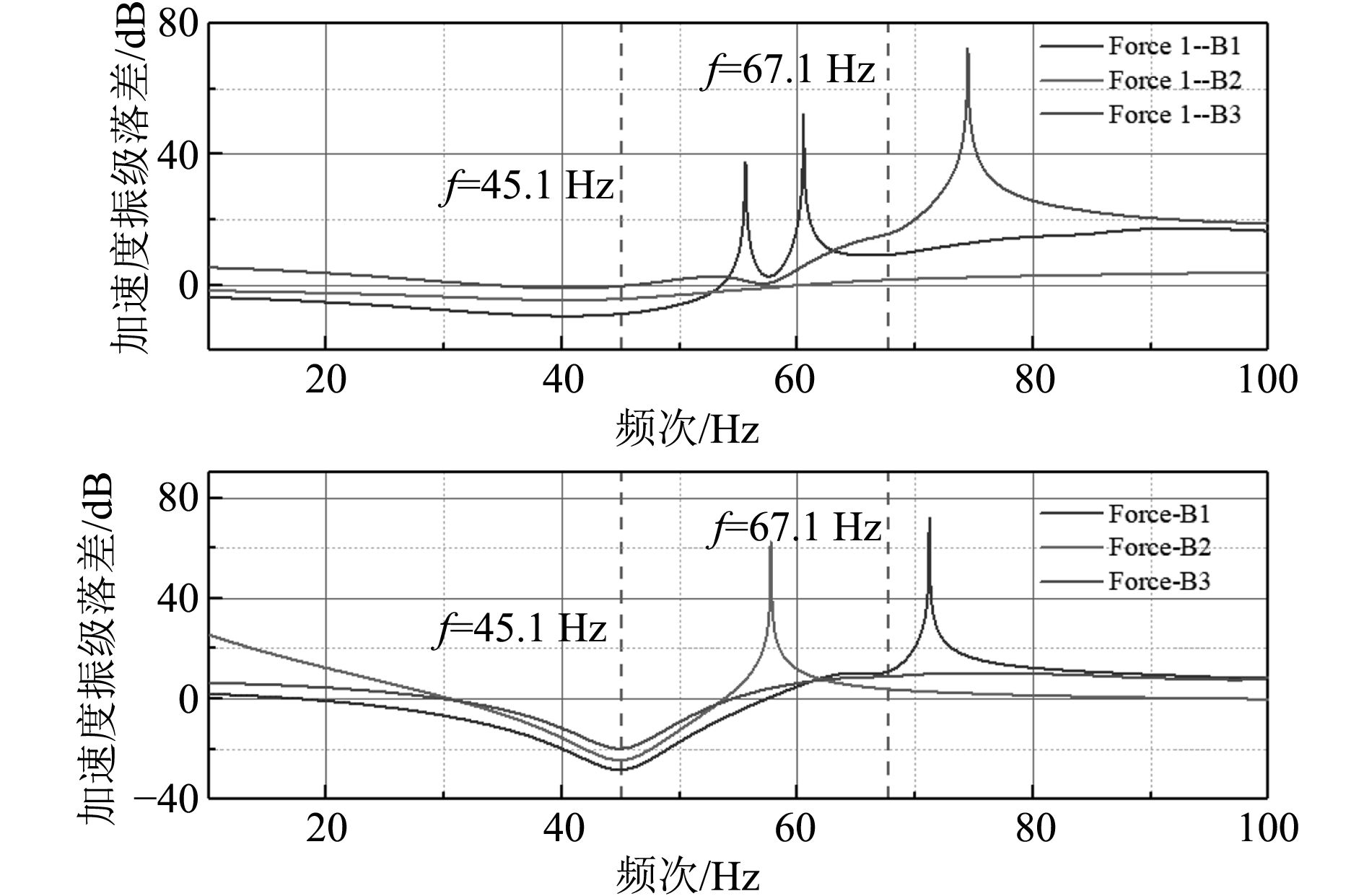
运用Abaqus进行静力强度校核和振动传递研究,同样舱段两端采用简支约束,得到其前3阶固有频率为41.73 Hz,62.12 Hz,68.85 Hz。以Force点为激励点,分析激励点Force传递至桁架B1点及基座F1点的加速度振级落差,在0~1 000 Hz范围内F1点的加速度振级落差为38.42 dB。
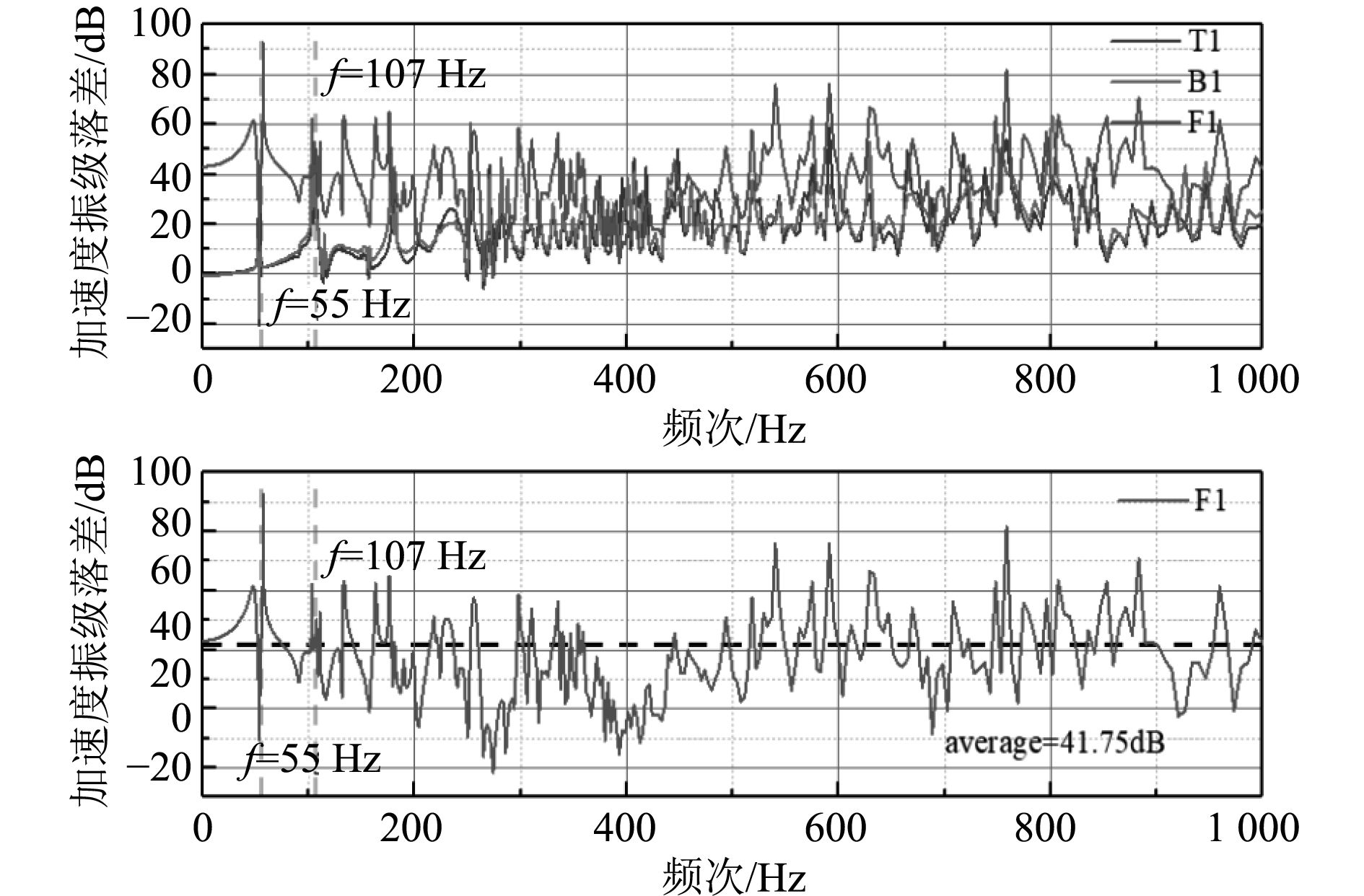
4.2 复材桁架浮筏仿真用复合材料代替钢材,采用相同约束,仿真结果表明F1在1~1000 Hz内的平均加速度振级落差为41.75 dB,且在复合材料桁架顶部承受1 000 kg静载下最大等效应力值为69.56 MPa,最大变形值为0.332 mm,复合材料在减轻重量的同时隔振性能提高了3.33 dB,达到41.75 dB。

|
图 12 复材桁架浮筏静力强度校核 Fig. 12 Check of static strength of truss floating raft |
|
图 13 复材桁架浮筏各点加速度振级落差 Fig. 13 Acceleration vibration level difference at each point of the floating raft |
将测试复材桁架独立条件下的振动传递特性,采用吊带约束浮筏桁架顶部两侧的垂向自由度。
在复合材料桁架浮筏材料管内装配上述含沙量75%的周期振子,周期振子采用周期均匀布置,并将周期振子与复材管内壁胶接固定,为保证装配的精度和内部材料的连续性,在碳纤维复合材料管靠近端面的空隙部分填充树脂胶。

|
图 14 复合材料桁架浮筏装配图 Fig. 14 Assembly drawing of composite truss floating raft |
以Force1为激励点进行频响试验得到B1,B2,B3响应点的加速度随时间衰减曲线做快速傅里叶变换得到加速度随频率的变化曲线,以10 E−6 m/s2为参考值得到各响应点的加速度振级,继而得到各响应点对于激励点的加速度振级落差。
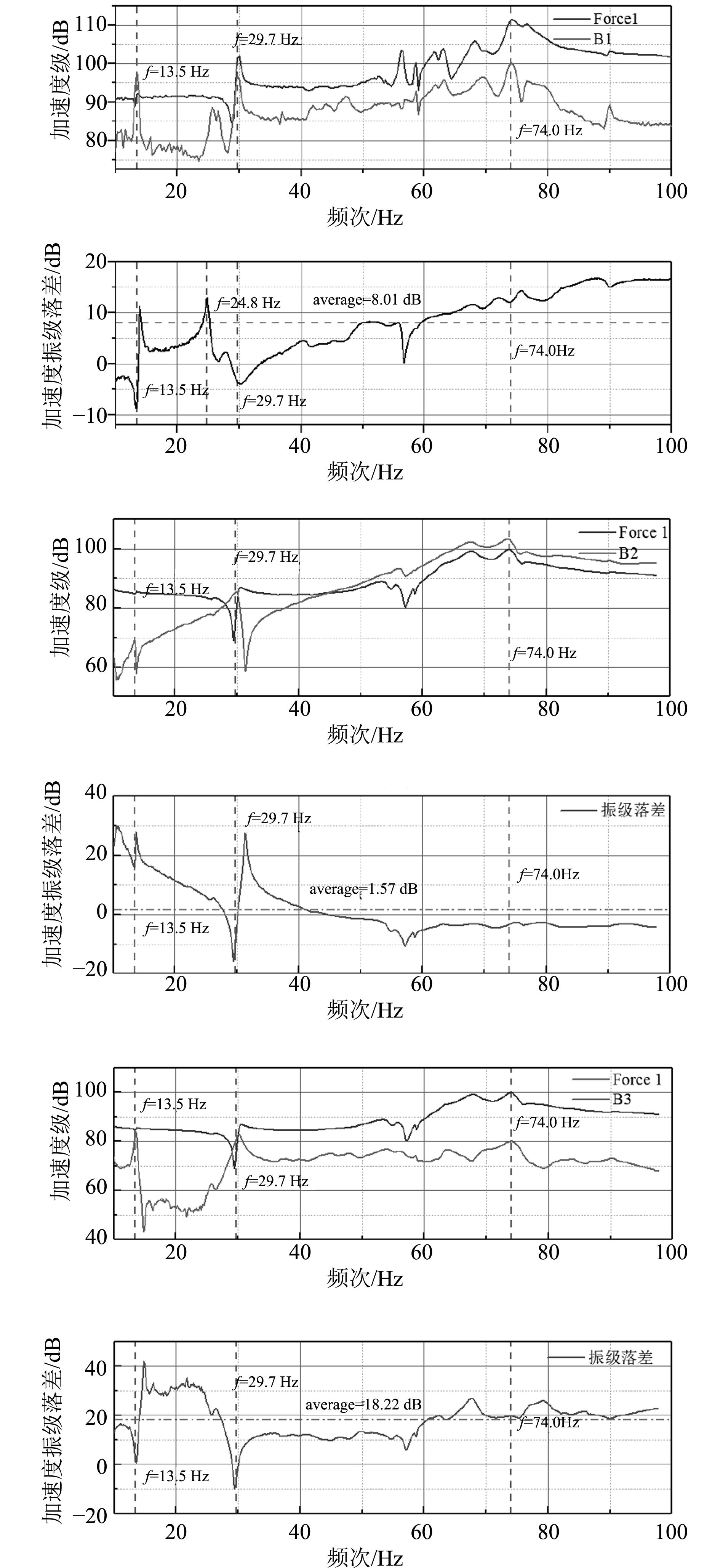
|
图 15 Force1至B1,B2,B3加速度振级落差 Fig. 15 Force1 to B1, B2, B3 acceleration vibration level difference |
在低频段10~100 Hz范围内,Force 1点加速度响应总体远远大于B1,其平均加速度振级落差为8.01 dB,在10~100 Hz范围内,B2点的加速度响应大于激励点Force1,其平均加速度振级落差为1.57 dB,在10~100 Hz范围内,B3点的平均加速度振级落差为18.22 dB,这是由于复合材料桁架浮筏在顶部横向两侧采取吊装简支约束,加之B3点距激励点Force1点远大于B2点,且传递途径中横向构件较多。
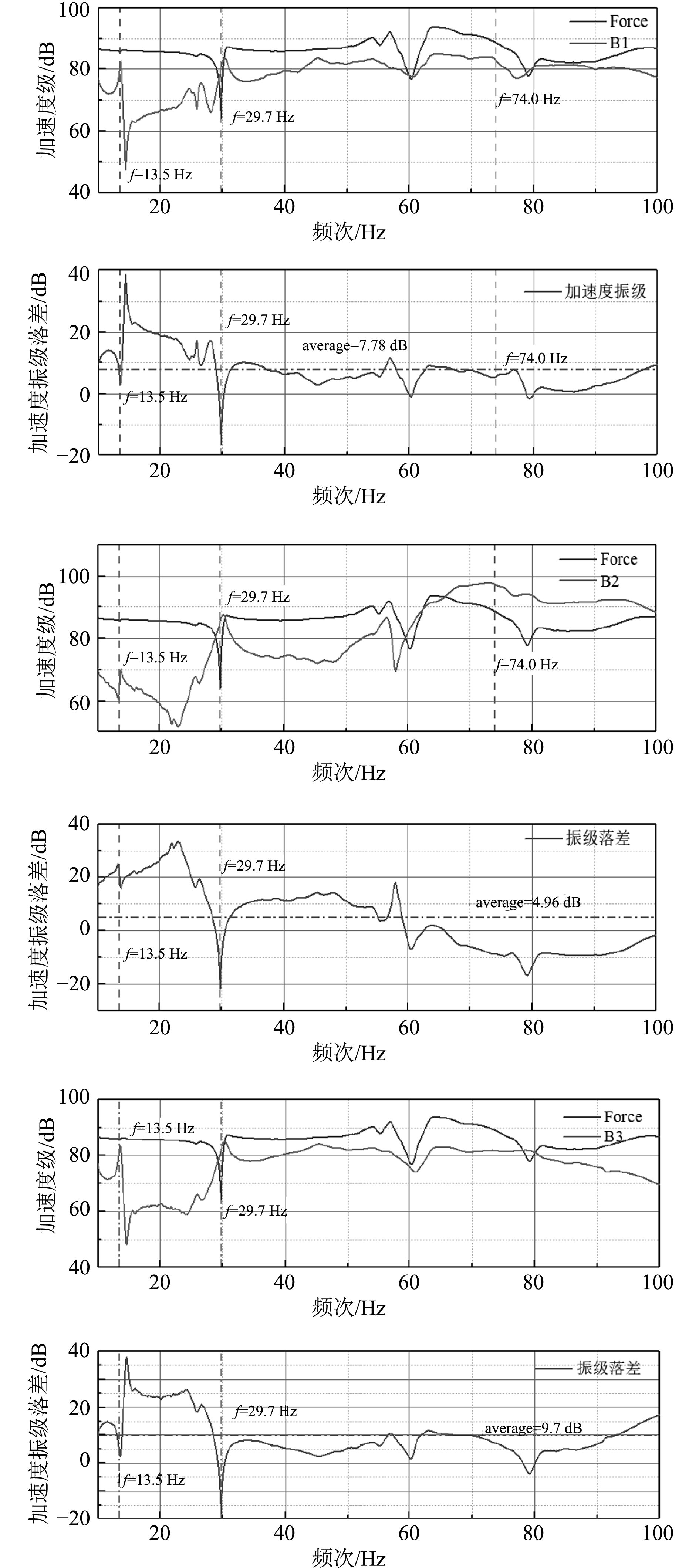
|
图 16 Force至B1,B2,B3加速度振级落差 Fig. 16 Force to B1, B2, B3 acceleration vibration level difference |
以Force为激励点进行频响试验得到B1,B2,B3各响应点的加速度振级落差。在10~100Hz范围内,激励点Force至B1点的平均加速度振级落差为7.78 dB,小于Force1点至B1点的加速度振级落差,激励点Force至B2点的平均加速度振级落差为4.96 dB,激励点Force至B3点的平均加速度振级落差为9.7 dB。
复合材料桁架浮筏在未填充均质沙时,Abaqus仿真结果如图17所示。
|
图 17 复合材料桁架浮筏加速度振级落差仿真 Fig. 17 Simulation of acceleration vibration level difference of composite truss floating raft |
仿真结果与试验结果如表5所示,均表明结构的振级落差在第一阶固有频率后逐渐增大,在填充均质沙后,各激励点至各响应点的加速度振级落差均有增加。
|
|
表 5 10~1 000 Hz范围内各激励点下的加速度振级落差 Tab.5 Acceleration vibration level difference under each excitation point in the range of 10~1 000 Hz |
本文通过测试钢制圆管和复合材料管以及添加阻尼振子后,管件的固有频率和阻尼比的变化规律,求解其固有频率和阻尼比。由试验结果可得,复合材料的振动衰减性能远高于钢制管件。
探究复合材料管件内部填充不同比例的阻尼沙对管件阻尼性能的影响,结果表明,随着阻尼块中阻尼沙填充率的增加,管件的固有频率随之降低,但管件的阻尼比在填充率75%达到最大值为0.0229。
在对桁架浮筏结构进行优化时可将加速度振级落差提升3.61 dB,且用复材代替钢制材料时振级落差仍可提升3.33 dB。
在复合材料管中填充含沙量为75%的阻尼振子进行动态试验时各激励点至响应点的加速度振级落差均有增加。
| [1] |
牟文珺. 复合材基座对船舶设备振动传递的控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
|
| [2] |
GIBSON R F. Modal vibration response measurements for characterization of composite materials and structures[J]. Composites Science and Technology, 2000, 60(15): 2769-2780. DOI:10.1016/S0266-3538(00)00092-0 |
| [3] |
ABRAMOVICH H, GOVICH D, GRUNWALD A. Damping measurements of laminated composite materials and aluminum using the hysteresis loop method[J]. Progress in Aerospace Sciences, 2015, 78: 8-18. DOI:10.1016/j.paerosci.2015.05.006 |
| [4] |
HONG Y, HE X D, WANG R G. Vibration and damping analysis of a composite blade[J]. Materials and Design, 2012, 34(2): 98-105. |
| [5] |
VESCOVINI, RICCARDO, BISAGNI, et al. A procedure for the evaluation of damping effects in composite laminated structures[J]. Progress in Aerospace Sciences, 2015.
|
| [6] |
赵树磊, 郭万涛, 吴医博. 复合材料基座减振性能试验研究[J]. 材料开发与应用, 2009, 24(04): 8-13. DOI:10.3969/j.issn.1003-1545.2009.04.003 |
| [7] |
洪明, 陈浩然, 寇长河. T300/QY8911复合材料层合板梁动力响应试验研究[J]. 玻璃钢/复合材料, 2000(5): 3-5. |
| [8] |
BHUDOLIA S K, GOHEL G, LEONG K F , et al. Damping, impact and flexural performance of novel carbon/Elium® thermoplastic tubular composites[J]. Composites Part B, 2020, 203. |
| [9] |
杨睿, 王壮, 李晓彬, 等. 舰艇浮筏隔振系统的发展与趋势[J]. 船舶工程, 2020, 42(7): 28-34. |
| [10] |
陈剑, 邓海华, 程用超, 等. 浮筏减振装置减重及控制方法研究[J]. 机电设备, 2019, 36(4): 12-15+19. |
| [11] |
方同, 薛璞. 振动理论及应用[M]. 西安: 西北工业大学出版社, 1998.
|
| [12] |
况成玉, 张志谊, 华宏星. 周期桁架浮筏系统的隔振特性研究[J]. 振动与冲击, 2012, 31(2): 115-118+135. DOI:10.3969/j.issn.1000-3835.2012.02.023 |
 2022, Vol. 44
2022, Vol. 44
