2. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003
2. School of Civil Engineering and Architecture, Jiangsu University of Science and Technology, Zhenjiang 212003 , China
随着现代反舰武器的发展,航空炸弹、超高音速反舰导弹等反舰武器对大型水面作战舰船的威胁越来越大。上层建筑作为舰船指挥控制中心,最易受到空中武器的攻击,虽然上层建筑在全船中所占比例较小,但功能划分区域较多,一旦受损舰船将迅速失去战斗能力。因此,舰船上层建筑的防护性能将直接影响到舰船的整体安全和作战性能。
国内外学者对舰船在爆炸载荷作用下的结构响应开展了大量的研究。Houlston和Slater[1-2]对空中爆炸载荷作用下的加筋板结构响应进行试验,将试验结果与数值结果进行对比,发现二者基本吻合。吴迪等[3]利用MSC.Dytran对空中非接触爆炸载荷作用下舰船动态响应过程进行了数值模拟,对船体结构应力情况、能量吸收以及冲击环境进行分析。柯力[4]以船舶上层建筑结构为研究对象,对远场爆炸载荷作用下舰船结构的防护性能进行研究,得到爆炸参数和结构参数对夹层板结构抗爆性能的影响规律。
本文以某舰船上层建筑为研究对象,通过Dytran模拟空中爆炸载荷作用下舰船上层建筑结构的动态响应过程。分别从冲击波的传播、结构应力分布和结构毁伤变形等方面进行分析,得到其结构的响应规律及力学特性。
1 空中爆炸理论爆炸冲击波的破坏能力主要通过冲击波的峰值超压
| $ {I_ + } = \int_0^{{\tau _ + }} {P\left( t \right)} {\rm{d}}t 。$ | (1) |
Hopkinson[6]提出爆炸相似定律:对于2个几何相似的填充炸药,如果两者的炸药成分相同,尺寸不同,则在同一大气环境中发生爆炸时,在相同比例距离处的冲击波相似。Henrych[7]通过大量试验数据,总结空中爆炸现象及爆炸载荷传播规律,得到冲击波峰值超压、正压持续时间、比冲量等参数的函数表达式。
| $ \Delta p(t) = \Delta {p_m}\left(1 - \frac{t}{\tau }\right){{\rm{e}}^{ - \alpha t/\tau }} 。$ | (2) |
正压区的作用时间即冲击波正压持续时间,
| $ {\tau _ + } = B \cdot \sqrt R \sqrt[6]{W} 。$ | (3) |
比冲量
| $ \begin{split}& \dfrac{{I}_+}{\sqrt[3]{W}}=663-\dfrac{1115}{Z}+ \dfrac{629}{{Z}^{2}} - \dfrac{100.4}{{Z}^{3}}\quad(0.4 \leqslant Z \leqslant 0.75),\\ &\dfrac{{I}_+}{\sqrt[3]{W}}=-32.2+\dfrac{211}{Z}-\dfrac{216}{{Z}^{2}}+\dfrac{80.1}{{Z}^{3}}\quad(0.75 < Z\leqslant 3)。\end{split}$ | (4) |
式中:
基于舰船设计图纸利用有限元软件Patran建立上层建筑有限元模型,采用笛卡尔直角坐标系,X轴与船体基线重合,船首方向为正方向;Y轴与中线面垂直,左舷方向为正方向;Z轴与水线面垂直,向上为正方向。该舰船上层建筑舱室共分3层,自上而下分别为驾驶甲板及其下围壁、上桥楼甲板及其下围壁、下桥楼甲板及其下围壁,板架结构为横骨架式。整个上层建筑为船体结构的FR134~FR158部分,长22.55 m,宽18.6 m,高7.5 m,如图1所示。
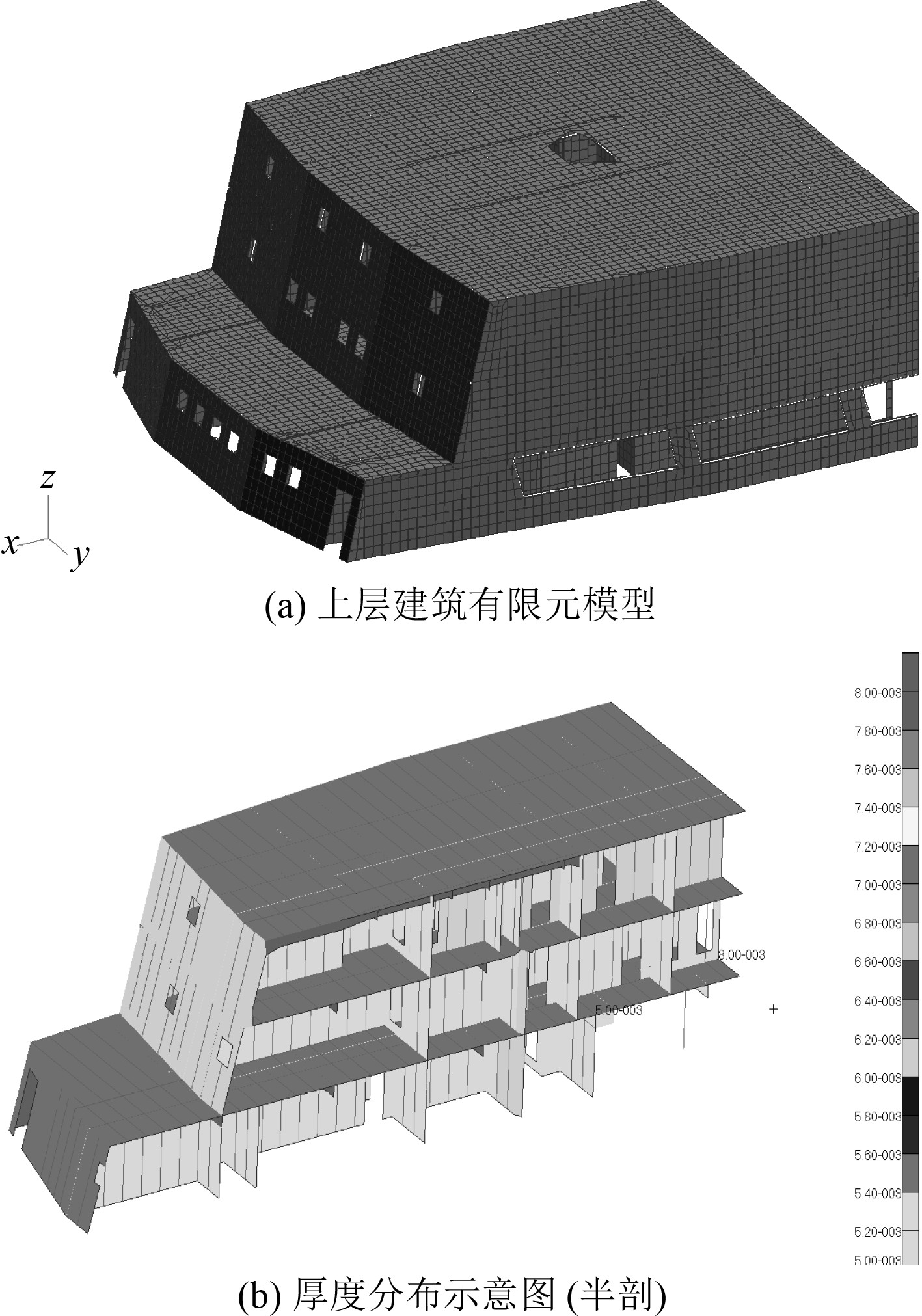
|
图 1 舰船上层建筑有限元模型 Fig. 1 Finite element model of warship superstructure |
舰船上层建筑结构所用材料为高强度907A钢,材料的弹性模量为
| $ \frac{{{\sigma _d}}}{{{\sigma _y}}} = 1 + {\left( {\frac{{\dot \varepsilon }}{D}} \right)^{\frac{1}{p}}} 。$ | (5) |
式中:
空气和炸药材料采用Gamma律状态方程来进行描述,Gamma律状态方程为:
| $ P = \left( {\gamma - 1} \right)\rho e 。$ | (6) |
式中:e为单位质量比内能,其中空气比内能为
本文采用多欧拉耦合方法数值模拟舰船上层建筑结构与爆炸冲击载荷的相互作用,将上层建筑外部空气设为欧拉域,尺寸为24 m×20 m×20 m,欧拉域中网格采用BOX卡片进行划分,在保证计算精度的前提下,为了节省计算时间,通过BIAS卡片将空气域设为渐变分布。将上层建筑外表面结构与空气域之间定义耦合面,耦合面上的开口用哑元单元进行封闭;在爆炸载荷作用下,结构可能会出现破损失效,因此耦合面需要定义失效模式。同时在空气域边界定义流入、流出命令来避免爆炸冲击波在欧拉域的边界发生反射。
2.4 计算工况进行水面舰艇空中爆炸工况设计时,综合考虑不同舱室受攻击的概率、结构强度和对舰艇生命力的重要程度,选取上层建筑结构中的指挥舱室作为研究对象。炸药设在指挥舱室上甲板(Fr155和L3P交点)正上方3.5 m处,沿-Z轴方向选取N1(驾驶甲板)、N2(上桥楼甲板)、N3(下桥楼甲板)为观测点,在结构外表面(L3S)上选取S1,S2,S3,S4为测点,如图2所示。
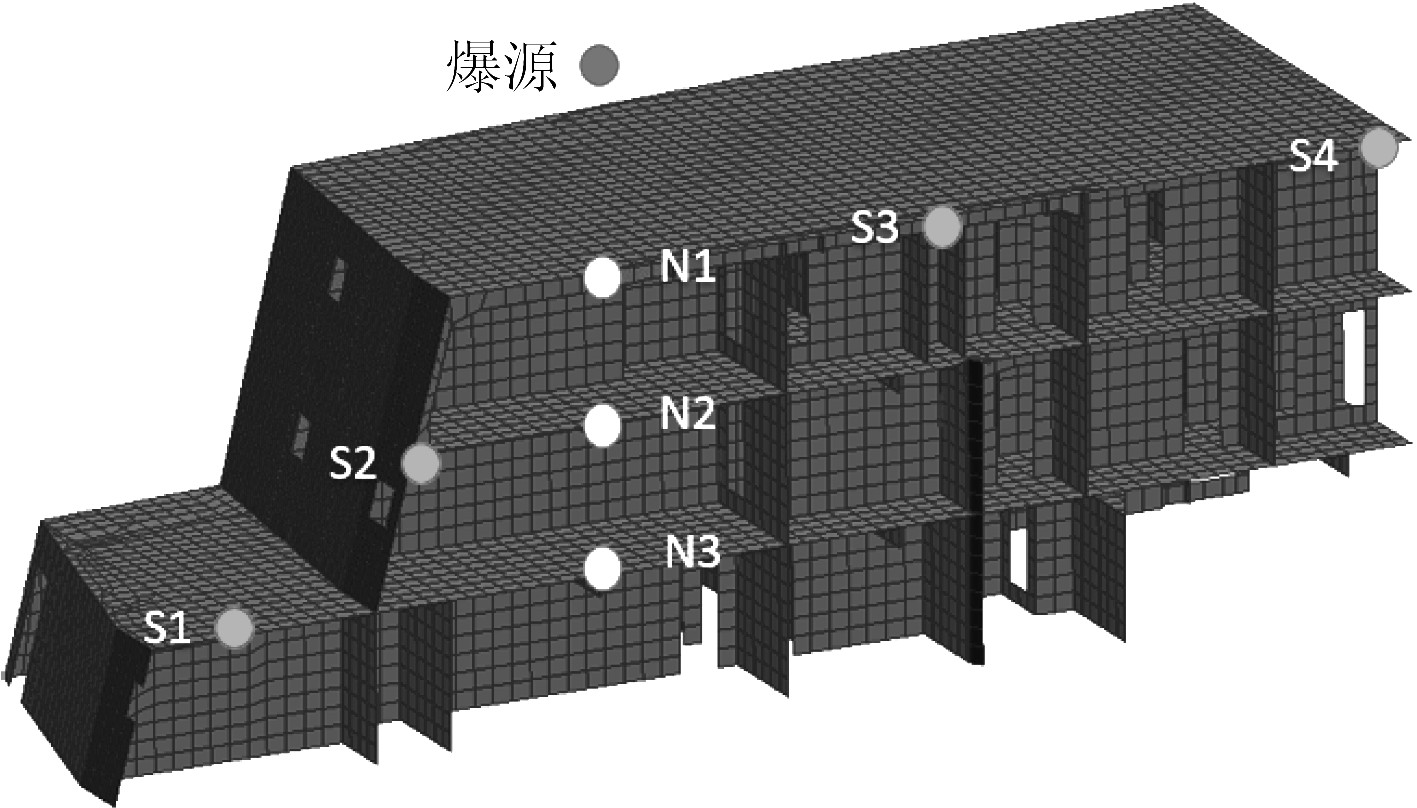
|
图 2 特征点位置示意图 Fig. 2 Schematic diagram of feature point location |
因炸药种类较多,在实际计算中采用能量相似原理进行等效,根据炸药的比爆热将其实际装药量转换为相应的TNT装药量,计算工况如表1所示。
|
|
表 1 计算工况 Tab.1 Calculation conditions |
上层建筑结构在不同炸药量作用时的冲击波传播具有相似性,因此以S40结果为例进行说明,图3为空中爆炸冲击波作用下舰船上层建筑结构在不同时刻的压力分布云图。可以看出:压力波以爆源为中心呈球形向外扩散,随着正压区面积增大,其波阵面的超压峰值不断衰减。当波阵面到达驾驶甲板时,流场质点运动受阻碍而产生反射和绕射现象,反射波和后续入射波叠加形成反射超压现象;绕射波和入射波在驾驶甲板发生汇聚,形成高密度能量团,同时冲击波沿结构围壁发生绕射现象。随着冲击波能量的耗散、转化,空气域压力逐渐恢复正常。
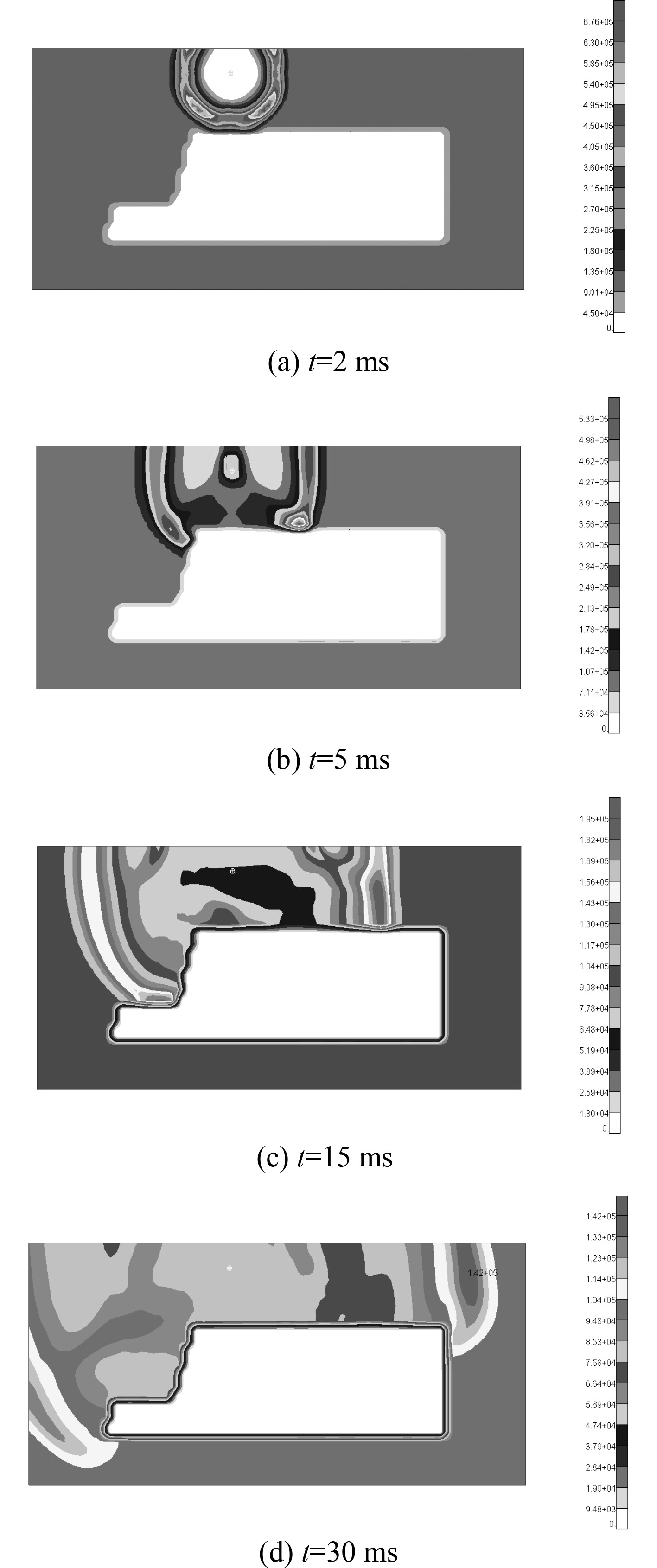
|
图 3 空气域压力分布云图 Fig. 3 Cloud map of air pressure distribution |
图4为舰船上层建筑结构特征点压力时间历程曲线,表2为L3S特征点参数表。可以看出,冲击波到达距爆源最近的N1测点,其压力迅速达到0.645 MPa,但其正压时间最短,只有1.3 ms。冲击波在上层建筑前围壁结构传播时,没有产生明显的能量汇聚,测点S2的压力峰值(0.172 MPa)只有N1测点的25.9%;随着冲击波继续传播,绕射波和入射波在下桥楼甲板汇聚,测点S1的压力峰值(0.198 MPa)比测点S2提高15%,且正压时长增加0.5 ms,如图4(a)所示。冲击波在驾驶甲板沿−X轴方向传播时,N1测点绕射波和S4测点入射波发生汇聚,S4测点压力仅次于N1测点,其压力峰值(0.326 MPa)。综上所述,峰值超压
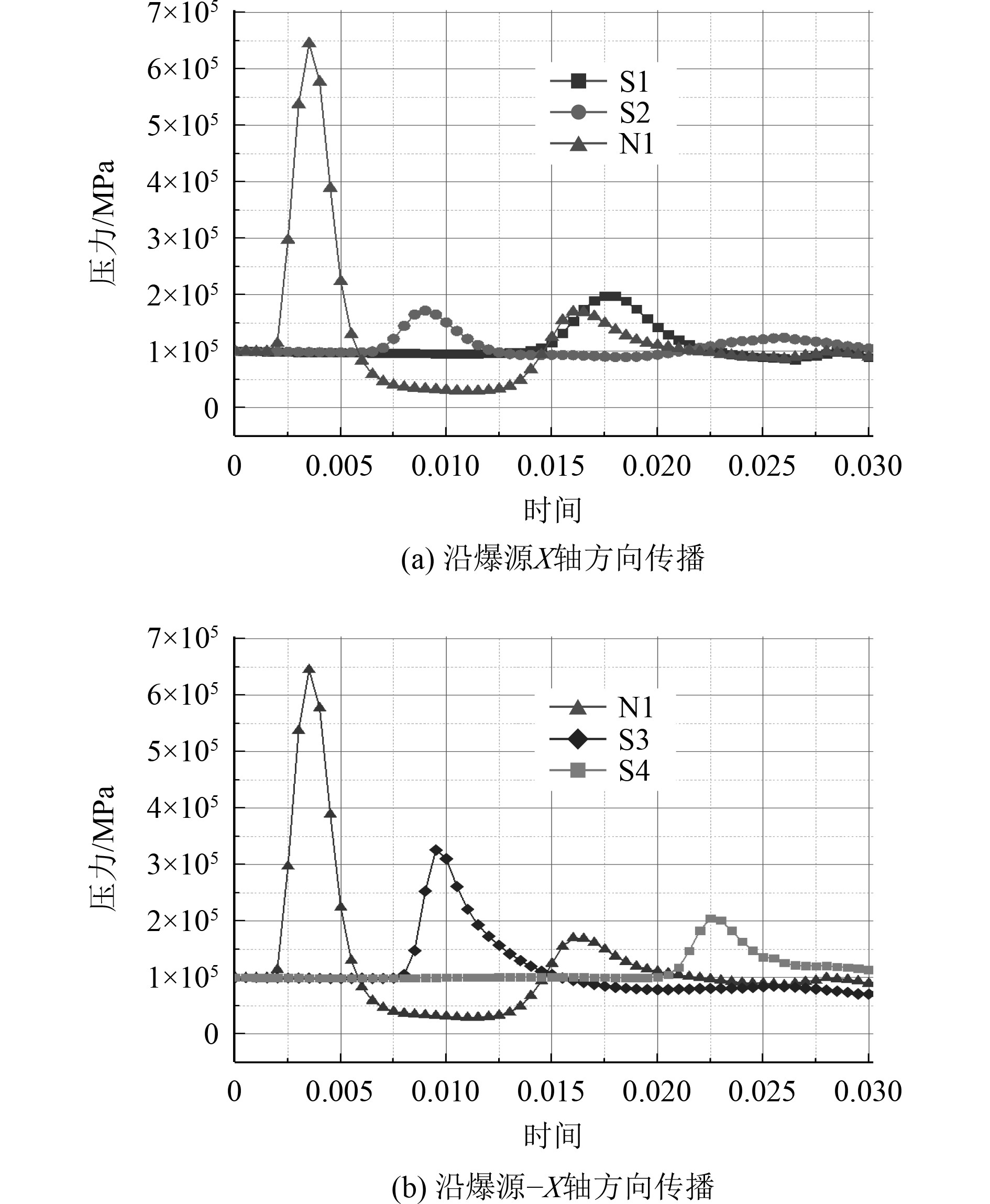
|
图 4 特征点压力时间历程曲线 Fig. 4 Pressure history curve of characteristic points |
|
|
表 2 L3S特征点参数 Tab.2 Parameter at characteristic points of L3S |
图5为空爆载荷作用下舰船上层建筑结构在不同时刻的应力分布云图。为了清楚地观察内部结构应力分布情况,以半剖模型为例进行说明。从图中可以看出,在爆炸初始时刻,舰船上层建筑在冲击波的作用下产生结构响应,应力波以近似圆形向四周传播,在30 ms时结构趋于稳定。图中显示结构最大应力(504 MPa)大于静态屈服应力,强应力区域主要集中在迎爆面、舱室角隅和强力构件交接处。从图5(b)可以看出,Z轴作为冲击波正压方向,其应力的传递速度大于X,Y轴方向。在5 ms时,冲击波传播至驾驶甲板围蔽结构时,应力已传至下桥楼横舱壁结构,说明应力波的传播速度大于冲击波的传播速度。
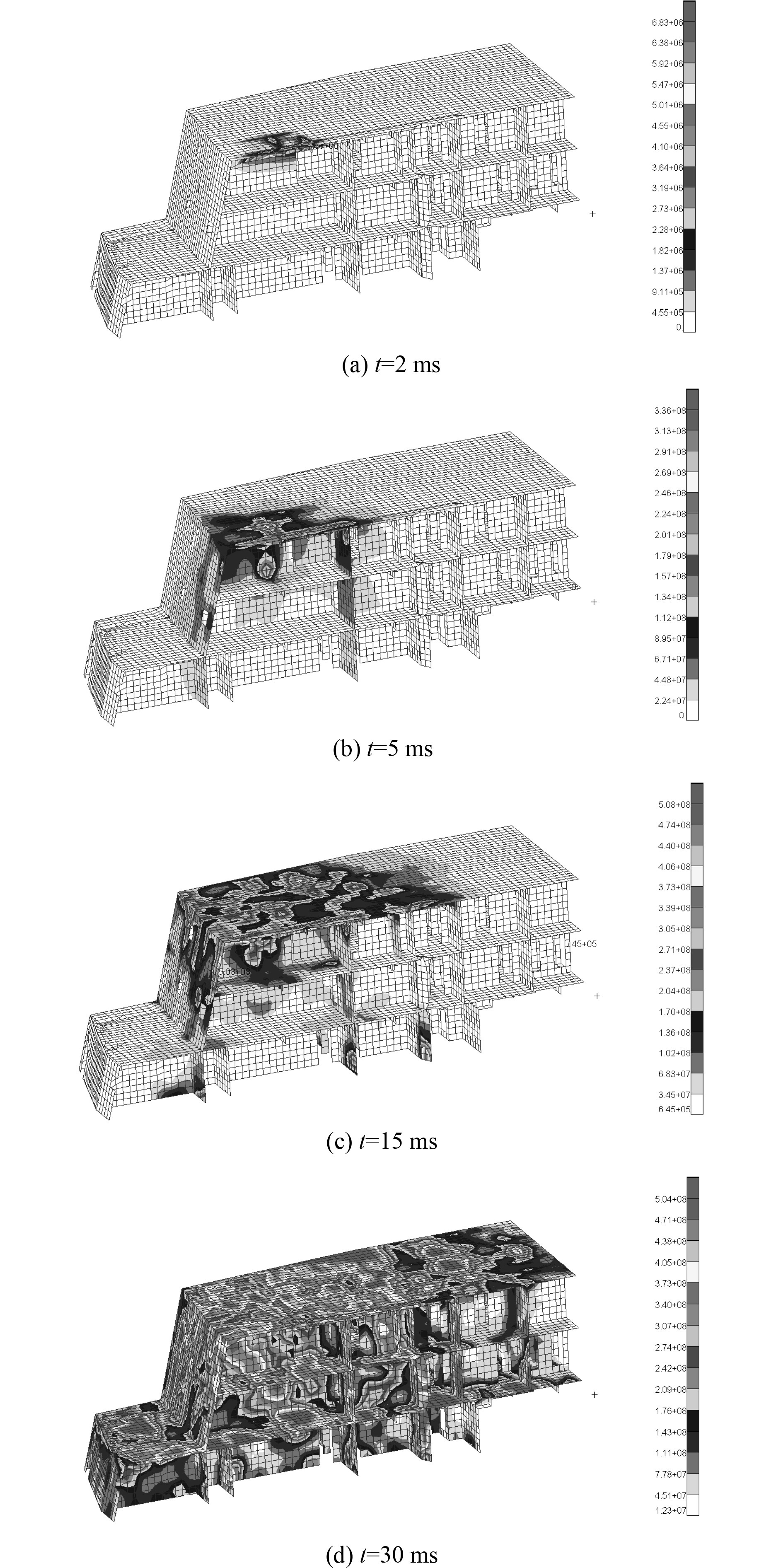
|
图 5 结构应力分布云图(S40) Fig. 5 Stress distribution of superstructure(S40) |
为了观测上层建筑结构在爆炸载荷下的响应,在结构不同位置选取特征点,其应力变化规律如图6所示。驾驶甲板作为迎爆面,其测点应力迅速达到峰值398 MPa,正压时间结束后出现衰减。应力通过与驾驶甲板相连的舱壁结构向上、下桥楼结构传递,N2和N3测点应力稳步增长,但能量在传递过程不可避免发生转移扩散和衰减现象,因此N2和N3测点应力增长速率相对N1测点较缓,如图6所示。
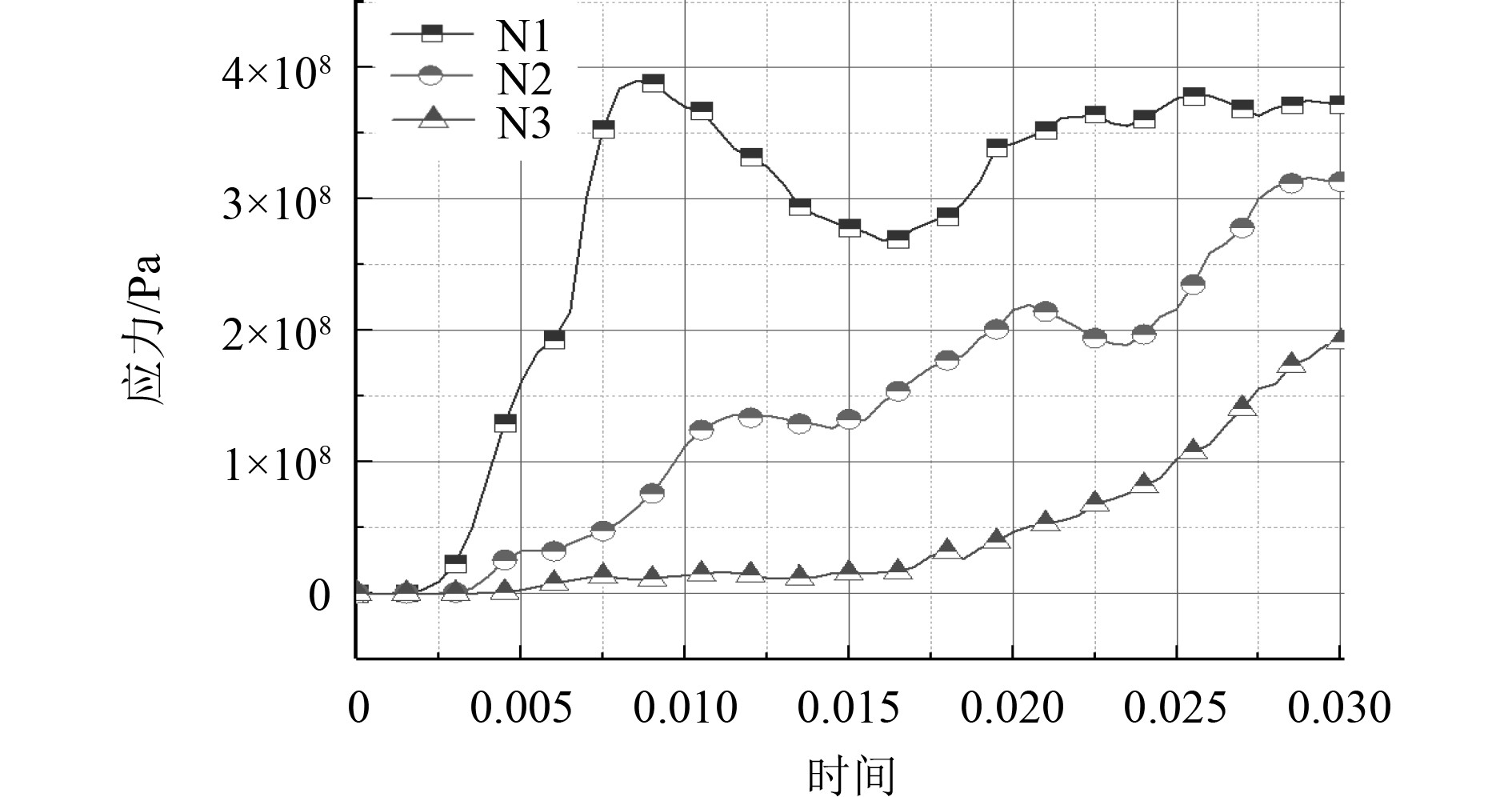
|
图 6 特征点应力时间历程曲线(S40) Fig. 6 Pressure-time history curve of characteristic points (S40) |
爆炸冲击波会使舰船上层建筑结构产生一定的塑性变形,图7为30 ms时舰船上层建筑结构在空爆载荷作用下毁伤变形云图。上层建筑结构作为舰船指挥控制中心,内部舱室复杂,较多的开口导致结构整体强度下降,因此塑性变形较大。结构塑性变形主要集中在驾驶甲板结构,结构最大应变没有达到材料的失效应变,因此没有产生失效单元。迎爆面受冲击载荷的直接作用,面内结构发生拉伸凹陷变形,且具有明显的局部效应。与迎爆面连接的舱壁结构在驾驶甲板结构的挤压和爆炸冲击波的作用,舱壁结构边部单元出现压溃变形,中心区域单元产生凸起膨胀变形。上层建筑结构开口结构出现折皱变形。舰船上层建筑结构的变形单元主要集中在裸露在空外部气域中的甲板结构,其内部结构和围蔽结构变形面积和形变量相对较小。
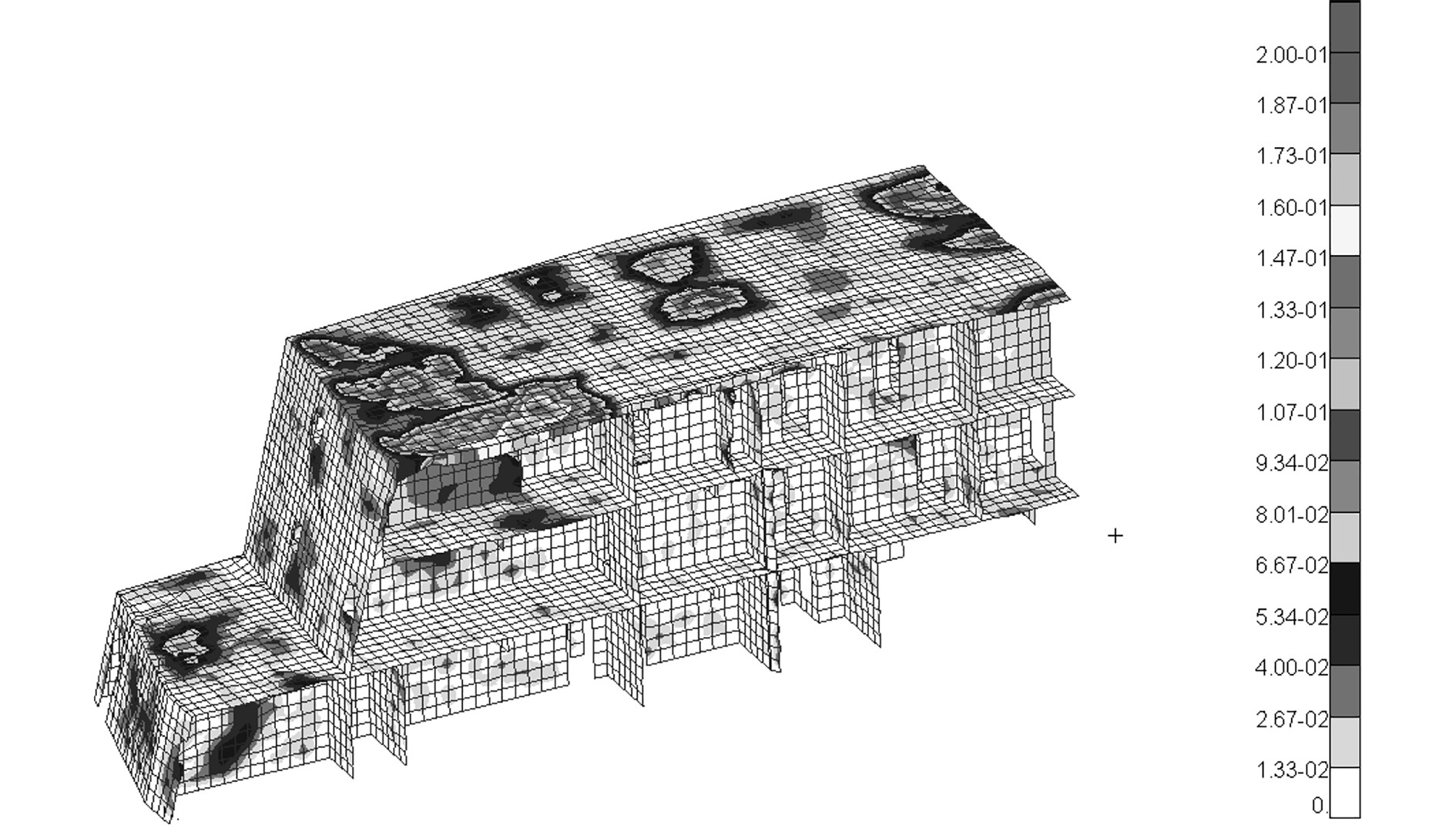
|
图 7 上层建筑结构毁伤变形云图(S200) Fig. 7 Cloud image of damage and deformation of superstructure (S200) |
驾驶甲板结构作为迎爆面,其变形面积和形变量最大,N1测点最大变形为0.242 m,由于此时结构材料处于弹塑性阶段,当正压作用结束后,N1测点变形量有较大的回弹。随着应力的传递和结构的挤压作用,上桥楼甲板结构出现塑性变形,N2测点最大变形为0.052 m,N3测点变形量相对较小,可忽略不计,如图8(a)所示。不同爆炸工况下,N1测点在12 ms时变形量达到峰值,此后压缩区介质开始反向压缩,N1测点上部空气域压强开始回升,在结构内外压力差和材料弹塑性的共同作用下,NI测点位移开始回落。如图8(b)所示。
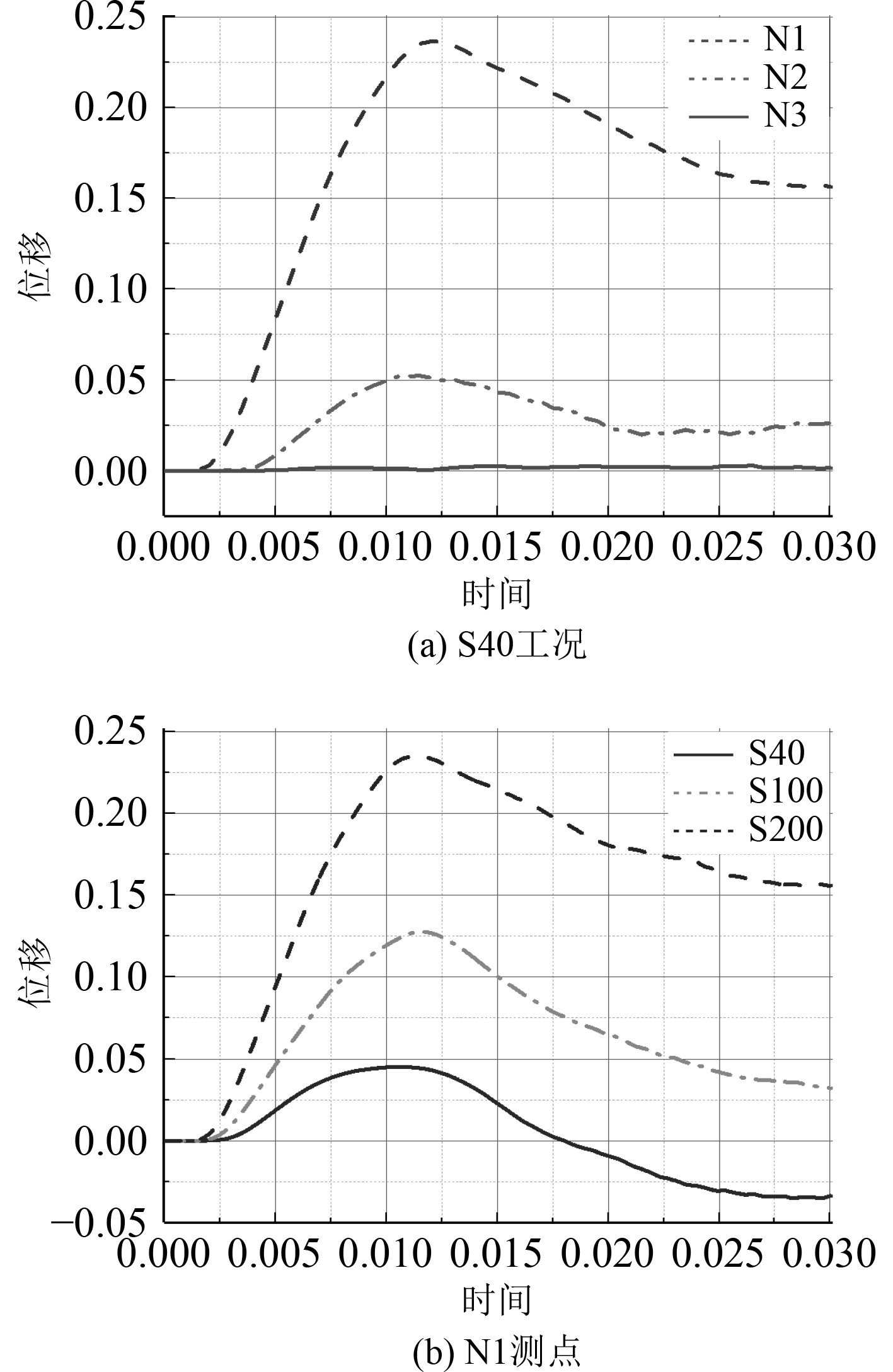
|
图 8 特征点位移时间历程曲线 Fig. 8 Displacement history curve of characteristic points |
舰船结构主要通过破损、变形等形式消耗、吸收冲击波能量,为了说明空中爆炸载荷对舰船结构所造成的损伤,表3统计了不同工况下舰船上层建筑结构的塑性变形能吸收情况。可以看出,驾驶甲板结构是主要的吸能构件,占比70%以上,其次是下桥楼结构,上桥楼结构吸能量占比最少,不足10%。结构整体吸能量随着炸药量的增加而增加,在冲击波反射超压作用下,驾驶甲板结构形变量增大,吸能占比由71.6%增长到81.7%,同时上、下桥楼结构吸能占比都出现不同程度的降低。
|
|
表 3 上层建筑结构吸能表(MJ) Tab.3 Energy absorption table of offshore platform structure |
本文以某舰船上层建筑作为研究对象,开展了空中爆炸载荷作用下舰船上层建筑结构的响应规律及力学特性研究。通过从冲击波的传播规律、结构应力分布和结构毁伤变形特性等方面进行分析,得到的主要结论如下:
1)空中爆炸冲击波在舰船上层建筑结构的空气流场中传播时,峰值超压
2)冲击波在舰船上层建筑结构外部流场中传播时,结构与冲击波入射夹角越小,发生能量汇聚概率越低;上层建筑围壁结构处的压力峰值和正压时长低于距爆源相同距离的甲板结构,说明结构与冲击波入射夹角越小。
3)空中爆炸冲击波对舰船上层建筑的结构毁伤模式以压溃变形为主,其驾驶甲板结构吸能量占比70%以上,而下桥楼结构次之,上桥楼结构占比低于10%。
| [1] |
HOULSTONHE R. Finite strip analysis of plates and stiffened subjected to air-blast loads[J]. Composite Structure, 1989, 32(3): 647-659. |
| [2] |
HOULSTONHE R, SLATER J E, PEGG N, et al. On analysis of structural response of ship panels subjected to air blast loading[J]. Composite Structure, 1995, 21: 273-289. |
| [3] |
吴迪, 张世联. 空中爆炸下舰船动态响应数值模拟[J]. 舰船科学技术, 2007, 29(6): 165-168. |
| [4] |
柯力. 钢质夹层板上层建筑结构防护性能优化及抗爆试验研究[D]. 镇江: 江苏科技大学, 2019.
|
| [5] |
韩阳. 爆炸载荷及其作用下的舰船结构响应数值模拟[D]. 武汉: 华中科技大学, 2019.
|
| [6] |
孙业斌. 爆炸作用与装药设计[M]. 北京: 国防工业出版社, 1987.
|
| [7] |
HENRYCH J, ABRAHAMSON G R. The dynamics of explosionand its use[M]. Amsterdam Elsevier Scientifi Pub, 1979.
|
| [8] |
李营, 汪玉, 吴卫国. 船用907A钢的动态力学性能和本构关系[J]. 哈尔滨工程大学学报, 2015, 36(1): 127-129. |
| [9] |
朱锡, 张振华, 梅志远. 舰船结构毁伤力学[M]. 北京: 国防工业出版社, 2013.
|
 2022, Vol. 44
2022, Vol. 44
