2. 广东理工学院 信息技术学院,广东 肇庆 526100
2. Department of Information Technology, Guangdong Polytechnic College, Zhaoqing 526100, China
船舶遥感图像监测是通过无人机、卫星等航空航天设备对水面船舶进行识别监测的技术。船舶遥感图像的特点在于信息获取速度快、识别范围广、受地形影响小、信息更新周期短等,因此遥感图像监测识别技术可以实现全天候、高分辨率、实时精准的监控目标。但是遥感图像由于图像分辨率高,如果监测目标的尺度、倾斜度以及高宽比变化比较大,则可能会出现漏检、误检等现象。随着遥感图像技术的快速发展,遥感图像的数量急剧上升,因此如何从数据量巨大并且背景干扰强、监测目标特性不确定的情况下,快速且准确地自动识别出船舶,这对遥感图像识别技术有着巨大挑战。作为一种回归分析方法,多元线性拟合方法以数理统计为基础,将多个变量拟合成线性相关关系,实现相关信息的加工处理。本文以多元线性拟合方法为基础,研究船舶遥感图像条带噪声分离技术。
1 多元线性拟合方法 1.1 多元线性拟合模型常用的多元线性拟合数学模型如下式:
| $ {y_i} = {\alpha _0} + {\alpha _1}{x_{1i}} + \cdots + {\alpha _k}{x_{ki}} + {\varepsilon _i},i = 1,2,\cdots,n\text{。} $ | (1) |
式中:yi为因变量;x1i,…,xki为自变量;当k值为1时,式(1)则是一元线性拟合模型;当
和一元线性拟合模型相比,多元线性拟合的参数估计要复杂很多,可以通过矩阵,将单变量总体扩展到多变量总体。假设存在一个样本集(yi,x1i,x2i,…,xki),i=1,2,…,n,则该样本集可以转换成下式:
| $ \begin{array}{*{20}{c}} {{y_1} = {\alpha _0} + {\alpha _1}{x_{11}} + \cdot \cdot \cdot + {\alpha _k}{x_{k1}} + {\varepsilon _1}}\text{,} \\ {{y_2} = {\alpha _0} + {\alpha _1}{x_{12}} + \cdot \cdot \cdot + {\alpha _k}{x_{k2}} + {\varepsilon _2}}\text{,} \\ \vdots \\ {{y_n} = {\alpha _0} + {\alpha _1}{x_{1n}} + \cdots + {\alpha _k}{x_{kn}} + {\varepsilon _n}} \text{。} \end{array} $ | (2) |
式中:k为自变量的个数;α0,α1,…,αk为自变量的系数;εi为随机变量。式(2)的矩阵形式如下式:
| $ \left[ {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ \vdots \\ {{y_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{{x_{11}}}& \cdots &{{x_{k1}}} \\ 1&{{x_{12}}}& \cdots &{{x_{k2}}} \\ \vdots & \vdots &{}& \vdots \\ 1&{{x_{1n}}}& \cdots &{{x_{kn}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _0}} \\ {{\alpha _1}} \\ \vdots \\ {{\alpha _k}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ \vdots \\ {{\varepsilon _n}} \end{array}} \right]\text{。} $ | (3) |
式(3)可以表示为下式:
| $ {{{\boldsymbol{y}} = {\boldsymbol{x}}\alpha + \varepsilon }}\text{。} $ | (4) |
如果存在样本
| $ {\mathbf{\hat \alpha }} = \left[ {\begin{array}{*{20}{c}} {{{\hat \alpha }_0}} \\ {{{\hat \alpha }_1}} \\ \vdots \\ {{{\hat \alpha }_k}} \end{array}} \right]\text{,}{\mathbf{\hat \varepsilon }} = \left[ {\begin{array}{*{20}{c}} {{{\hat \varepsilon }_1}} \\ {{{\hat \varepsilon }_2}} \\ \vdots \\ {{{\hat \varepsilon }_n}} \end{array}} \right] ,$ |
则可以得到样本矩阵,如下式:
| $ {{{\rm{y}} = {\rm{x}}\hat \alpha + \hat \varepsilon }}\text{,} $ | (5) |
式中的回归方程可以表示为:
| $ {\hat y_i} = {\hat \alpha _0} + {\hat \alpha _1}{x_{1i}} + \cdots + {\hat \alpha _k}{x_{ki}}\text{。} $ | (6) |
式中:
得到多元线性拟合模型之后,则需要对公式中的各项参数进行估计。
1.2 多元线性模型拟合优度和显著性检验得到多元线性拟合模型的估计参数之后,则可以构建出多元线性拟合方程,得到的多元线性拟合方程需要进行显著性检验。
在多元线性拟合模型的拟合优度检验中,通过判定系数R2来判断多元线性拟合方程的好坏,根据拟合度优先检验方式,可以得到下式:
| $ SST = SSR + SSE\text{。} $ | (7) |
式中:SST为离差和;SSR为回归平方;SSE为残差平方。优合度系数可以用下式表示:
| $ r = \frac{{{cov} \left( {X,Y} \right)}}{{\sqrt {DX \cdot DY} }}\text{,} $ | (8) |
判定系数R2可以用下式表示:
| $ {R^2} = 1 - \frac{{SSE}}{{SST}}\text{。} $ | (9) |
在一元线性拟合模型中,判定系数R2的值越接近1,则线性拟合模型和实际的测量值之间的拟合度就越好,如果判定系数R2的值越靠近0,则说明拟合度越差。在多元线性拟合模型中,如果自变量增加,则判定系数R2也会变大,但是此时的判定系数R2的数值增大和多元线性模型的拟合度没有直接关系,因此需要对判定系数R2的公式进行调整,则可以得到调整之后的多元线性拟合模型的拟合优度,如下式:
| $ R_1^2 = 1 - \frac{{SSE}}{{n - k - 1}}/\frac{{SST}}{{n - 1}}\text{,} $ | (10) |
式中:
在多元线性拟合模型的显著性检验中,F检验和可以用下式表示:
| $ {\sum\limits_{i = 1}^n {\left( {{y_i} - \bar y} \right)} ^2} = {\sum\limits_{i = 1}^n {\left( {{y_i} - {{\hat y}_i}} \right) + \sum\limits_{i = 1}^n {\left( {{{\hat y}_i} - \bar y} \right)^2} } }\text{,} $ | (11) |
假设Lyy=Q+U,则可以得到下式:
| $ F = \frac{U}{{Q/\left( {n - 2} \right)}} \sim F\left( {1,n - 2} \right)\text{。} $ | (12) |
当拒绝域ε0={F>F1-∝(1,n−2)},则表示多元线性拟合模型的拟合效果比较好。
2 船舶遥感图像技术 2.1 船舶遥感图像信号特征分析船舶遥感图像系统的特点在于三高以及三多,三高是指空间分辨率高、时间精度高以及光谱分辨率高,三多是指平台多、传感器多、角度多,因此船舶遥感图像信号的特征主要有高空间分辨率、几何形状、数学统3个。
作为船舶遥感图像的主要特征之一,高空间分辨率是指分辨率可以达到10 m以内的船舶遥感图像。
船舶遥感图像的几何特点包括大小、形状、边缘、纹理、位置、组合以及活动等,在所有这些船舶遥感图像的特征中,边缘特征和纹理特征是船舶遥感图像最重要的特征。
船舶遥感图像本质上是其电磁辐射的能量图,并且这种电磁辐射能量的分布在时间和空间上都是连续的,在任意时刻t、不同的极化方向P以及波长λ下,船舶传感图像能够收集到坐标(x,y)目标辐射出来的能量值L,可以用下式表示:
| $ L\left( {x,y,t,\lambda ,p} \right) = (1 - \beta )E + \beta I\text{。} $ | (13) |
式中:β为目标船舶反射率;E为船舶的电磁波发射能量;I为船舶的入射量;P为极化方向;λ为电磁波的波长,t为船舶遥感图像的成像时间。
2.2 船舶遥感图像信号噪声分析船舶遥感图像信号的噪声主要是在获取遥感图像的过程中采集数据受到了多重干扰导致的,这些数据干扰信号主要来自于各类人造干扰源、空间环境干扰以及遥感设备自身的因素等。船舶遥感设备通过CCD图像传感器进行船舶图像的获取,在获取船舶图像的过程中不可避免地产生了各类图像噪声,根据船舶传感图像的噪声类型,可以将船舶传感图像噪声分成光电散粒、条带以及脉冲噪声。
其中船舶遥感图像条带噪声是一种原始的船舶遥感图像数据在一定程度上出现连续地偏高或者偏低的现象。船舶遥感图像的条带噪声无法使用斑点噪声降噪方法进行消除,并且船舶遥感图像的条带噪声和斑点噪声叠加在一起,会将真实的船舶图像信息进行掩盖,极大地降低了船舶遥感图像的质量,增加了船舶遥感图像的解读难度,会对船舶遥感图像的应用产生影响,因此在对船舶遥感图像进行解读之前,需要对船舶遥感图像进行条带噪声降噪处理。含有条带噪声的船舶遥感图像的模型可以用下式表示:
| $ {I_j}[i] = {S_j}[i] + R\left[ {i;{S_j}[i]} \right] + {N_j}[i],\begin{array}{*{20}{c}} {}&{i = 1, \cdots {N_c}} \end{array}\text{。} $ | (14) |
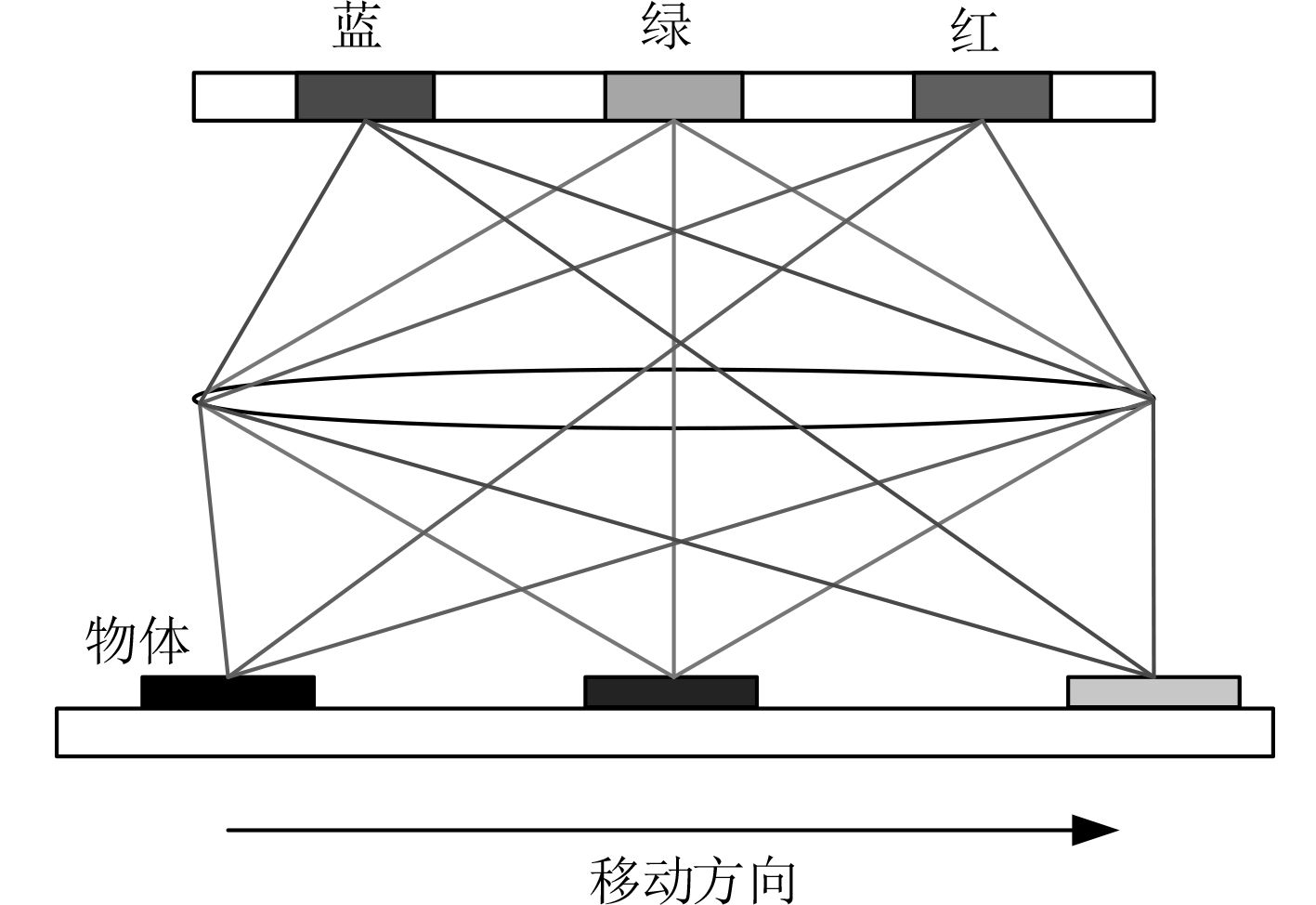
式中:Ij[i]为船舶遥感图像的像素值;Sj[i]为图像信号的入射幅值;Nj[i]为船舶遥感图像的点噪声;R[i;Sj[i]]为船舶遥感图像的条带噪声。CCD成像示意图如图1所示。
|
图 1 CCD成像示意图 Fig. 1 Schematic diagram of CCD imaging |
船舶遥感图像条带噪声的产生机制和其他点噪声的产生机制不一样,因此条带噪声和其他点噪声相比具有不同的特点,这也导致在图像中的表现不一样。假设船舶遥感图像中任意像素点的坐标为f(x,y),则理想的船舶遥感图像垂直条带噪声数学模型如下式:
| $ {f}_{v}\left(x,y\right)=\left\{\begin{array}{c}A\text{,}\\ 0,\end{array}\begin{array}{c}\forall x\in \left[{x}_{a},\cdots,{x}_{n}\right]\text{,} \\ {\rm{others}}\text{。} \end{array} \right.$ | (15) |
理想的船舶遥感图像水平噪声数学模型如下式:
| $ {f}_{{h}}\left(x,y\right)=\left\{\begin{array}{c}A\text{,}\\ 0,\end{array}\begin{array}{c}\forall y\in \left[{y}_{a},\cdots,{y}_{n}\right]\text{,}\\ {\rm{others}}。\end{array} \right.\text{,} $ | (16) |
实际的船舶遥感图像的垂直条带数学模型可以用下式(17)表示:
| $ {f}_{v}\left(x,y\right)=\left\{\begin{array}{l}f\left(x,y\right)\pm A\text{,}\hfill \\ f\left(x,y\right),\hfill \end{array}\begin{array}{c}\forall x\in \left[{x}_{a},\cdots,{x}_{n}\right],\\ {\rm{others}}。\end{array}\right. \text{,} $ | (17) |
水平条带的数学模型可以用下式:
| $ {f}_{\text{h}}\left(x,y\right)=\left\{\begin{array}{l}f\left(x,y\right)\pm A\text{,}\hfill \\ f\left(x,y\right),\hfill \end{array}\begin{array}{c}\forall y\in \left[{y}_{a},\cdots,{y}_{n}\right]。\\ others。\end{array}\right. \text{,} $ | (18) |
从船舶遥感图像的垂直条带数学模型以及水平条带的数学模型可以看出,船舶遥感图像的条带噪声的灰度值和相邻区域的非条带图像数值相比会偏大或者偏小,同时这种现象会导致船舶遥感图像的条带噪声的行和列的灰度均值或大或小,从而使得整个船舶遥感图像的灰度值变大或者变小。
4 船舶遥感图像条带噪声分离技术基于空间域和变换域是常用的两种船舶遥感图像去除噪声的方法。针对船舶遥感图像的像素,直接处理的方法是基于空间域的船舶遥感图像去噪方法;基于变换域的方法是将船舶遥感图像从空间域转换到变换域,然后基于变换域对船舶遥感图像中的噪声数据信息的表现形式进行分析,计算船舶遥感图像噪声数据的变换系数,最后再将船舶遥感图像进行变换域的逆变换,则可以得到分离噪声之后的船舶遥感图像数据信息。常见的变换域方法有余弦、小波以及傅里叶变换等,在船舶遥感图像去除条带噪声技术中,最常用的变换域方法是傅里叶和小波变换。
作为船舶遥感图像变换域中最基本的去噪方法,傅里叶变换去噪的基本思路是对船舶遥感图像进行傅里叶变换,获得噪声在遥感图像频谱中的频率分布,然后根据船舶遥感图像的图像数据信息和噪声数据信息在频域中不同的分布,将频域信息经过合适的滤波器进行滤波,滤除船舶遥感图像中的噪声信息之后,再将经过滤波之后的数据信息进行傅里叶逆变换,将船舶遥感图像从频域再次转换到空间域,最终获得去噪之后的船舶遥感图像。
作为线性系统分析的重要方法,傅里叶变换可以实现船舶遥感图像的空间域和频域之间的自由转换,部分无法在空间域中分析的遥感图像信息可以转换到频域中进行频谱分析,一维离散傅里叶变换如下式:
| $ F\left( u \right) = \frac{1}{N}\sum\limits_{x = 0}^{N - 1} {f\left( x \right)} {e^{ - j2\pi \frac{u}{N}x}}\text{,} $ | (19) |
一维离散傅里叶数学逆变换公式如下式:
| $ f\left( x \right) = \sum\limits_{x = 0}^{N - 1} {F\left( u \right){e^{ - j2\pi \frac{x}{N}u}}} \text{。} $ | (20) |
对船舶遥感图像进行傅里叶变换之后,则需要利用滤波器对船舶遥感图像中的噪声进行抑制或者消除。基于卷积定理,船舶遥感图像的噪声滤波器数学模型如下式:
| $ {\boldsymbol{G}}\left( {{\boldsymbol{u,v}}} \right){{ = {\boldsymbol{F}}}}\left( {{{{\boldsymbol{u}},{\boldsymbol{v}}}}} \right){\boldsymbol{H}}\left( {{{{\boldsymbol{u}},{\boldsymbol{v}}}}} \right)\text{。} $ | (21) |
式中:F(u,v)为含有噪声的船舶遥感图像的傅里叶变换之后的形式;H(u,v)为船舶遥感图像在频率域的滤波传递函数,该函数可以将遥感图像频域内的噪声进行衰减处理,然后得到降噪之后的形式G(u,v)。
最后将降噪之后的G(u,v)经过傅里叶逆变换,则可以得到降噪之后的船舶遥感图像,其基本原理如图2所示。

|
图 2 傅里叶滤波去噪原理 Fig. 2 Principle of Fourier filter denoising |
小波是指长度有限并且均值等于0的小区域波形,并且小波函数在时域中存在紧支集。对基波函数进行平移以及伸缩变换之后,则可以得到小波函数Ψa,b(t),如下式:
| $ {\psi _{a,b}}\left( t \right) = \frac{1}{{\sqrt {\left| a \right|} }}\psi \left( {\frac{{t - b}}{a}} \right)\text{。} $ | (22) |
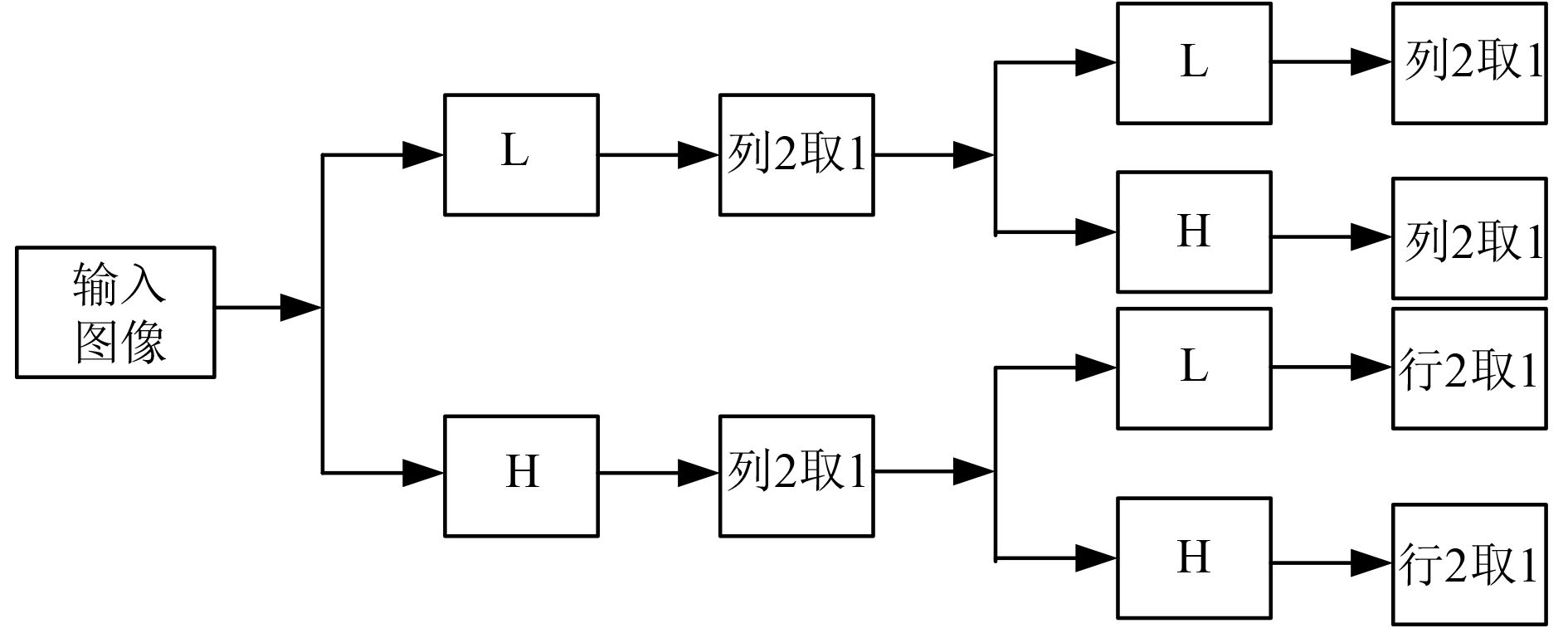
式中:a为缩放因子;b为平移因子。二维离散小波分解流程如图3所示。
|
图 3 二维离散小波分解流程 Fig. 3 Two dimensional discrete wavelet decomposition process |
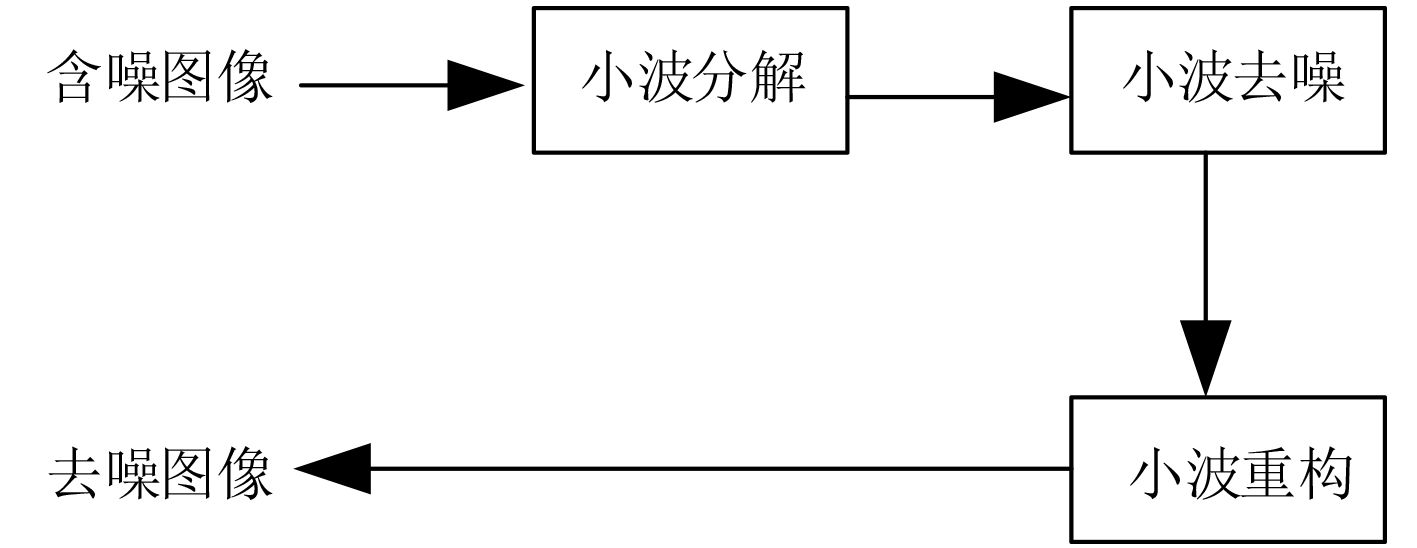
利用小波函数去噪主要有极大值、相关性以及阈值3种图像去噪方法,3种方法中小波阈值去噪方法由于方法简单得到了广泛的应用,其基本原理如图4所示。
|
图 4 基于阈值的小波去噪原理 Fig. 4 Wavelet denoising principle based on threshold |
遥感图像是对船舶进行监测的重要方式之一。但是由于船舶遥感图像系统的工作环境复杂、CCD器件自身的缺陷等原因,导致在对船舶遥感图像进行实际采集的时候产生多种噪声,这些噪声会降低船舶遥感图像的质量,严重影响后期对船舶遥感图像的应用,因此需要使用图像降噪技术对船舶遥感图像进行加工处理,以增加船舶遥感图像的清晰度。本文基于多元线性拟合模型,研究船舶遥感图像的条带噪声分离技术,提高图像质量。
| [1] |
严青, 张体强, 丁少华等. 一种基于多元线性拟合的多源噪声分离方法[J]. 噪声与震动控制, 2020, 40: 194-198. |
| [2] |
赵言, 花向红, 尹志永. 基于定权的多因子线性拟合方法研究[J]. 测绘工程, 2012, 21: 5-8. |
| [3] |
杨丽民, 郭志军. 多元离散函数的线性拟合及应用[J]. 当代化工, 2006, 35: 305-308. DOI:10.3969/j.issn.1671-0460.2006.04.025 |
| [4] |
兰红, 王璇. 基于多元线性回归的昆虫图像分割方法[J]. 计算机应用与软件, 2013, 30: 193-196. |
| [5] |
于希明, 洪硕, 于金祥等. 可见光遥感图像船舶目标数据增强方法研究[J]. 仪器仪表学报, 2020, 41: 261-269. |
| [6] |
陈跃. 基于光学遥感图像的船舶目标检测技术研究[J]. 舰船科学技术, 2016, 38: 121-123. |
| [7] |
孔祥阳, 彭群聂, 徐保根. 基于方向和结构特征的遥感图像条带噪声分离方法[J]. 电光与控制, 2020, 27: 6-11. |
| [8] |
王昶, 张永生, 王旭等. Landsat影像垂直方向条带噪声去除方法研究[J]. 华中科技大学学报, 2019, 47: 121-126. |
 2022, Vol. 44
2022, Vol. 44
