2. 北部湾大学 电子与信息工程学院,广西 钦州 535011
2. College of Electronic and Information Engineering, Beibu Gulf University, Qinzhou 535011, China
船舶航迹是内河船舶交通管理的关键依据。在实际船舶运行过程中,由于海风、海浪、天气等因素的影响,导致船舶航迹变化较大,获取的AIS数据会出现复杂、混乱的现象,无法准确地显示船舶航迹信息[1]。另外,AIS数据体量较大,已经达到了大数据级别,对其处理、应用难度较大,成为船舶航迹信息获取的主要阻碍因素之一。如何精确拟合船舶航迹,获取准确船舶航迹线,是目前船舶领域亟待解决的问题之一。
1 基于大数据分析的船舶航迹拟合方法 1.1 船舶航迹AIS数据获取与处理AIS数据是船舶航迹拟合的基础与前提,原始AIS数据是一串复杂晦涩的字符串,无法对其进行直接地理解与应用[2]。因此,在船舶航迹拟合之前,需要对AIS数据进行获取与处理,为后续目标船舶航迹拟合需求数据提取做准备。AIS数据获取过程即为ASCⅡ码解码过程,如图1所示。

|
图 1 AIS数据获取流程图 Fig. 1 AIS data acquisition flow chart |
通过图1所示流程即可获得船舶航迹AIS数据,为了方便研究的进行,对主要AIS数据进行适当的说明,具体如表1所示。
|
|
表 1 AIS数据说明表 Tab.1 AIS data description table |
由于人为、外界以及AIS设备自身等因素的影响,使得获取的AIS数据存在着一定的错误、偏差、冗余等现象,故在AIS数据应用之前,需要对其进行一定的预处理,以此来保障船舶航迹拟合的精准度[4]。经过大数据分析可知,AIS数据明显错误类型主要包含4种,具体如下:
1)船舶标识码错误,主要表现在MMSI长度上,常规MMSI长度为9位数,大于或小于9位数的MMSI均为错误数据;
2)经纬度超出合理范围。其中,经度合理范围为
3)航速与航向错误,例如航速小于0,航向大于360o;
4)AIS数据采集时间错误,不在规定采集时间内或者采集时间记录错误。
依据上述所展示的错误类型,对AIS数据进行处理,将错误数据进行删除,对缺失数据进行插补,以此来保障AIS数据的完整性与准确性,为后续航迹拟合需求数据提取奠定基础[4]。另外,经过大数据分析可知,AIS数据中包含时间、航向、航速、纬度、经度等多种船舶航迹相关信息,但是每种信息量纲均不同,故需要对其进行统一化处理:
| $ {R_i} = {\alpha ^ * }\lg {r_i} 。$ | (1) |
式中:Ri与ri为统一化处理后与前AIS数据集合;α*为辅助参数。
1.2 船舶航迹拟合需求数据提取以上述处理完成后的AIS数据为基础,应用数据挖掘算法对船舶航迹拟合需求数据进行提取,方便后续船舶航迹的拟合[5]。AIS数据中包含多种船舶航迹信息,但并不是每种信息均与航迹拟合有关系。根据已有文献研究可知,船舶航迹拟合只需要时间、经度与纬度信息[6]。船舶航迹由一系列点构成,呈现随机性、非线性、相关性、周期性等特征,具体特征内容如下:
1)随机性
船舶航迹容易受到不可控因素的影响,例如交通事故、驾驶员偏好、交通管制、天气环境等,致使船舶航迹具有随机性,很难对其进行预测;
2)非线性
在航道环境、天气、海浪等多种因素的共同作用下,船舶航迹具有较强的波动性,即非线性。
3)相关性
在一定时间内,船舶航迹呈现着出发地→目的地的整体大趋势[7]。因此,每一时刻的航迹之间存在着必然的联系,即相关性特征。
4)周期性
在较长时间区间角度出发,对于同一艘船舶来说,其航迹随着时间呈现着周期性的变化特征,主要体现在往返航迹中[8]。
对时间、经度与纬度信息进行提取[9]。其中,时间信息提取式为:
| $ T = \frac{{\left( {{\rm{Unix}}\_{\rm{time}} + {8^ * }3\;600} \right)}}{{86\;400}} + {70^ * }365 + 19 。$ | (2) |
式中:T是时间数据集合;Unix_time为AIS数据中的时间字段。
经度与纬度数据提取式为:
| $ \left\{ {\begin{array}{*{20}{c}} {L{o_i} = \dfrac{{{\rm{Unix}}\_{\rm{Longitude}}}}{{600\;000}} * \beta } ,\\ {L{a_i} = \dfrac{{{\rm{Unix}}\_{\rm{Latitude}}}}{{600\;000}} * \chi } 。\end{array}} \right. $ | (3) |
式中:Loi与Lai分别是提取的经纬度数据;Unix_Longitude与Unix_Latitude分别是AIS数据中的经度与纬度字段;β与χ是经度与纬度提取辅助参量,取值范围为[0,1]。
以时间为自变量,对船舶航迹拟合需求数据进行整理与集合,记为集合QT=(Lot,Lat),为后续船舶航迹拟合提供精确的数据支撑。
1.3 船舶航迹拟合实现采用线性拟合法与最小二乘曲线拟合法对船舶航迹进行分段拟合,获取准确的船舶航迹线[10]。应用高斯投影换算方法将经纬度数据转化为船舶坐标信息(大地坐标系),记为(xt,yt)。以此为基础,将船舶航迹划分为2个阶段,分别为直线阶段与曲线阶段,分别应用线性拟合法与最小二乘曲线拟合法进行航迹拟合[11]。
船舶航迹划分主要依据的是相邻时刻航向角(航向与水平坐标之间的角度)差值,划分依据为:
| $ \Bigg\{\begin{array}{cc}\mathrm{arctan}\dfrac{{y}_{t+1}}{{x}_{t+1}}-\mathrm{arctan}\dfrac{{y}_{t}}{{x}_{t}}=0,& 直线阶段,\\ \mathrm{arctan}\dfrac{{y}_{t+1}}{{x}_{t+1}}-\mathrm{arctan}\dfrac{{y}_{t}}{{x}_{t}}\ne 0,& 曲线阶段。\end{array} $ | (4) |
式中:
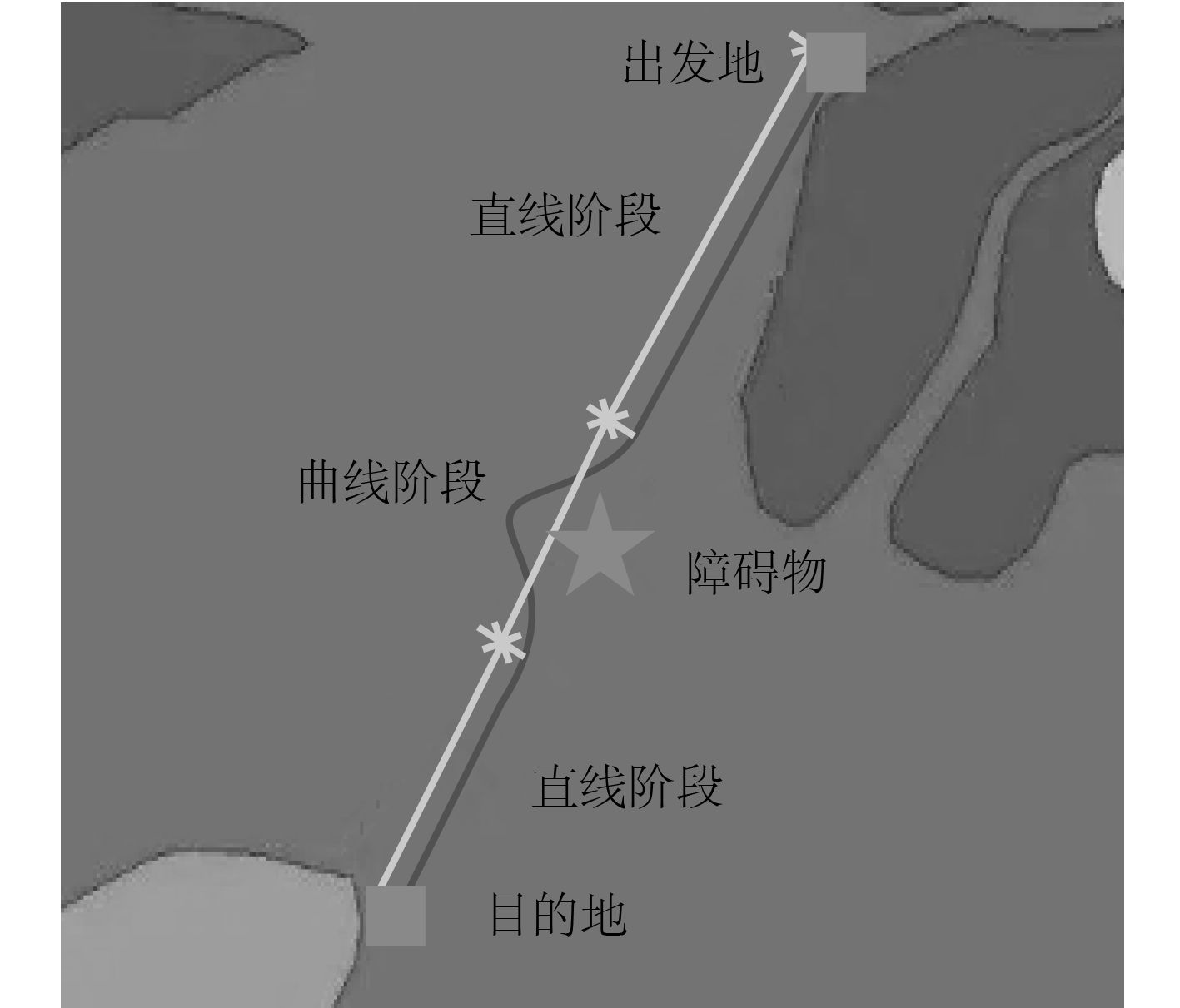
应用式(4)规则对船舶航迹进行划分,如图2所示。
|
图 2 船舶航迹划分示例图 Fig. 2 Example diagram of ship track division |
直线阶段船舶航迹拟合方程为:
| $ y = {a_1}x + {b_1} ,$ | (5) |
式中:a1与b1是航迹拟合方程的辅助参数。
当拟合残差平方和达到最小时,即可获得最佳的a1与b1参数值,求解方程表达式为:
| $ \min P = \sum\limits_{t = 1}^n {{{\left( {{y_t} - {a_1} - {b_1}{x_t}} \right)}^2}} 。$ | (6) |
求解式(6)即可获得参数a1与b1,计算结果为:
| $ \left\{ {\begin{array}{*{20}{c}} {{b_1} = \frac{{\displaystyle\sum\limits_{t = 1}^n {\left( {{x_t} - \bar x} \right)\left( {{y_t} - \bar y} \right)} }}{{\displaystyle\sum\limits_{t = 1}^n {{{\left( {{x_t} - \bar x} \right)}^2}} }}} ,\\ {{a_1} = \bar y - {b_1}\bar x} 。\end{array}} \right. $ | (7) |
式中:
将式(7)结果代入式(5),即可得到直线阶段船舶航迹拟合方程。
应用最小二乘法对船舶曲线阶段航迹进行拟合,有效去除干扰因素造成随机波动,使得拟合航迹更加平滑,与实际航迹更加契合,反映船舶的真实航行轨迹。曲线阶段船舶航迹拟合方程表达式为:
| $ y = \sum\limits_{t = 1}^n {{\delta _t}x} ,$ | (8) |
式中,δt是航迹拟合辅助参数,求解式为:
| $ \left[ {\begin{array}{*{20}{c}} {\sum {x_t^1} }& \cdots &{\sum {x_t^n} } \\ \vdots & \ddots & \vdots \\ {\sum {x_t^{n + 1}} }& \cdots &{\sum {x_t^{2n}} } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _1}} \\ \vdots \\ {{\delta _t}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sum {x_t^0{y_t}} } \\ \vdots \\ {\sum {x_t^n{y_t}} } \end{array}} \right] 。$ | (9) |
求解式(9)即可获得参数δt,代入式(8),即可得到曲线阶段船舶航迹拟合方程。
通过式(5)与式(8)即可实现船舶航迹的分段拟合,提供精准的船舶航迹信息。
2 实验与结果分析 2.1 实验准备阶段根据船舶航迹拟合实验需求,确定实验水域及其航迹数据获取装置。选取的实验水域应该有较少的障碍物,减少干扰因素对实验结论的影响。实验水域如图3所示。

|
图 3 实验水域图 Fig. 3 Experimental water area map |
航迹数据获取装置即AIS设备。根据航迹拟合需求,选取b-900型号AIS设备作为航迹数据获取装置。
2.2 实验结果分析 2.2.1 航迹拟合需求数据提取时延分析航迹拟合需求数据提取时延反映航迹拟合方法的数据分析效率。常规情况下,航迹拟合需求数据提取时延越短,表明航迹拟合方法的数据分析效率越高;反之,航迹拟合需求数据提取时延越长,表明航迹拟合方法的数据分析效率越低。通过实验获得航迹拟合需求数据提取时延如表2所示。可知,在不同实验工况背景下,应用提出方法获得的航迹拟合需求数据提取时延均小于最大限值,表明提出方法数据分析效率较高。
|
|
表 2 航迹拟合需求数据提取时延表 Tab.2 Delay table for data extraction of track fitting requirements |
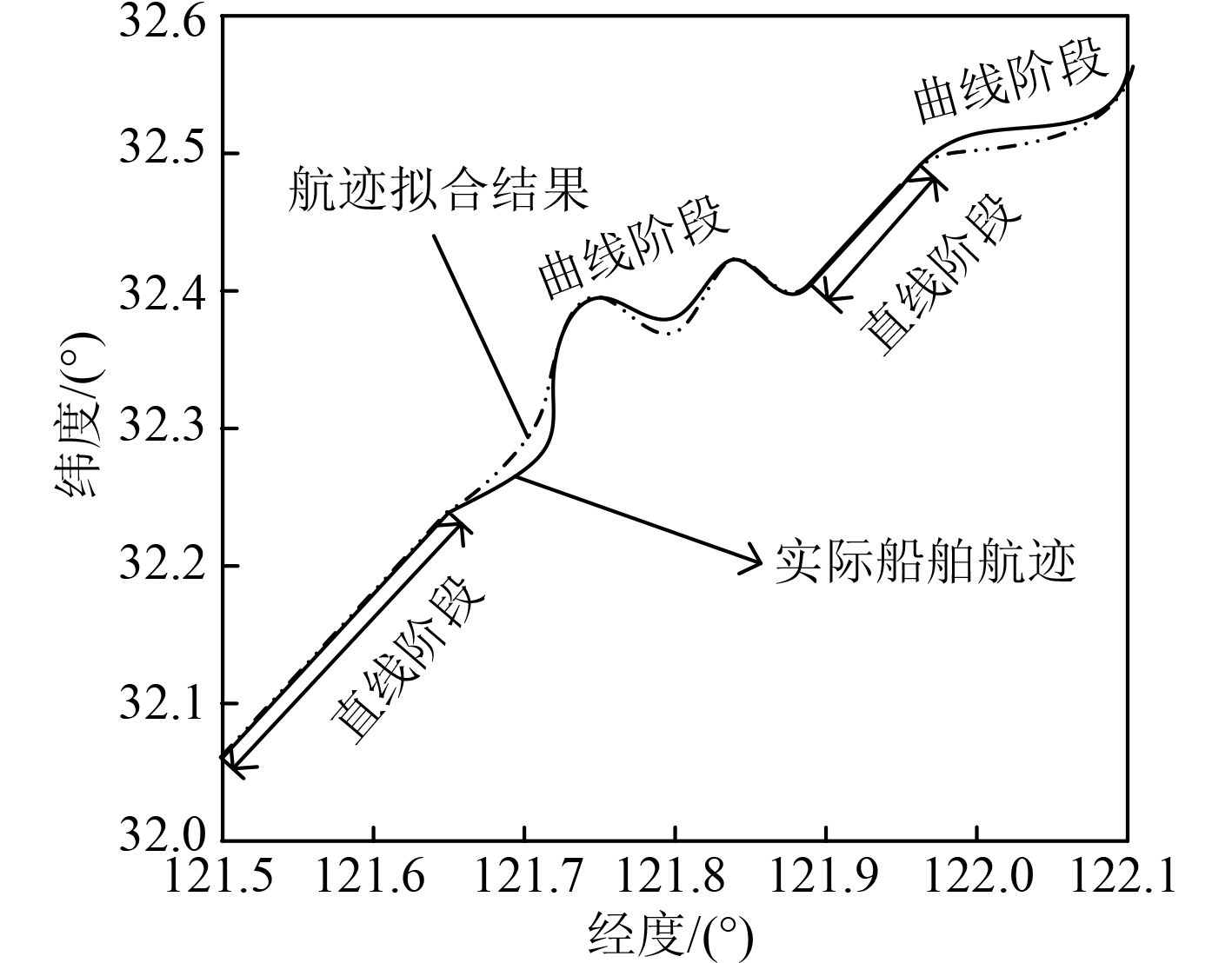
通过实验获得航迹拟合结果如图4所示。可知,应用提出方法获得的航迹拟合结果与实际船舶航迹几乎保持一致(直线阶段一致,曲线阶段存在些许误差),表明提出方法船舶航迹拟合效果较佳。
|
图 4 航迹拟合结果示意图 Fig. 4 Schematic diagram of track fitting results |
本文研究应用大数据分析技术(数据挖掘算法)提出新的船舶航迹拟合方法,应用提出方法获得的航迹拟合需求数据提取时延与航迹拟合误差均符合要求。
| [1] |
牟红梅, 胡青. 基于神经网络的异常船舶航迹特征因子模型[J]. 科学技术与工程, 2021, 21(34): 14610-14617. DOI:10.3969/j.issn.1671-1815.2021.34.021 |
| [2] |
胡玉可, 夏维, 胡笑旋, 等. 基于循环神经网络的船舶航迹预测[J]. 系统工程与电子技术, 2020, 42(4): 817-877. |
| [3] |
潘良, 唐星祝, 曾伟, 等. 基于大数据的配网电压智能分析及诊断应用研究[J]. 工程技术研究, 2021, 6(4): 20-21. DOI:10.3969/j.issn.1671-3818.2021.04.008 |
| [4] |
刘娇. 基于DE-SVM的船舶航迹预测模型[J]. 上海海事大学学报, 2020, 41(1): 34-39. |
| [5] |
李晓娜, 杨焱煜, 潘越. 基于机器学习算法的海空目标航迹数据分析技术研究[J]. 中国电子科学研究院学报, 2020, 15(1): 29-35. DOI:10.3969/j.issn.1673-5692.2020.01.006 |
| [6] |
王森杰, 何正伟. 基于生成对抗网络的船舶航迹预测模型[J]. 中国航海, 2021, 44(2): 72-77. DOI:10.3969/j.issn.1000-4653.2021.02.012 |
| [7] |
祝亢, 黄珍, 王绪明. 基于深度强化学习的智能船舶航迹跟踪控制[J]. 中国舰船研究, 2021, 16(1): 105-113. |
| [8] |
于琛, 付玉慧, 张逸飞, 等. 基于ARIMA-BIGRU的船舶航迹预测[J]. 船海工程, 2021, 50(6): 147-152. DOI:10.3963/j.issn.1671-7953.2021.06.030 |
| [9] |
张黎翔, 朱怡安, 陆伟, 等. 基于AIS数据的船舶轨迹修复方法研究[J]. 西北工业大学学报, 2021, 39(1): 119-125. DOI:10.3969/j.issn.1000-2758.2021.01.015 |
| [10] |
马兴民, 张勇. 基于光滑核函数多支持向量机的船舶航迹预测[J]. 数学的实践与认识, 2021, 51(20): 143-150. |
| [11] |
周宇, 曹英楠, 王永超. 面向大数据的数据处理与分析算法综述[J]. 南京航空航天大学学报, 2021, 53(5): 664-676. |
 2022, Vol. 44
2022, Vol. 44
