无线网络以其高精度、容错性和远程监控能力等特点,在船舶监控系统中得到广泛应用。无线传感器网络可以利用节点的时间和位置信息,获得基本的监控数据。但是在船舶监测中心的无线网络中,由于计算、存储、网络等方面的原因,导致了对数据进行定位的效率不高。王磊等[1]研究了基于高斯滤波的三维水声无线传感网络节点定位算法,利用高斯滤波算法对数据进行处理和距离估算,并利用多边形位置法求出未知节点的坐标;李娜等[2]研究了布谷鸟算法在无线传感器网络中的定位方法,基于最优对象的数学模型,利用杜鹃搜索法求出适应值函数,通过求取步长、推算概率等参数,从而确定未知节点的位置。上述方法虽然能够实现数据定位,但是容易受到周围环境等因素的影响,常出现定位错误等现象,为此设计一个无线网络的船舶监控中心多源数据定位方法,解决当前存在的问题,为数据定位提供参考。
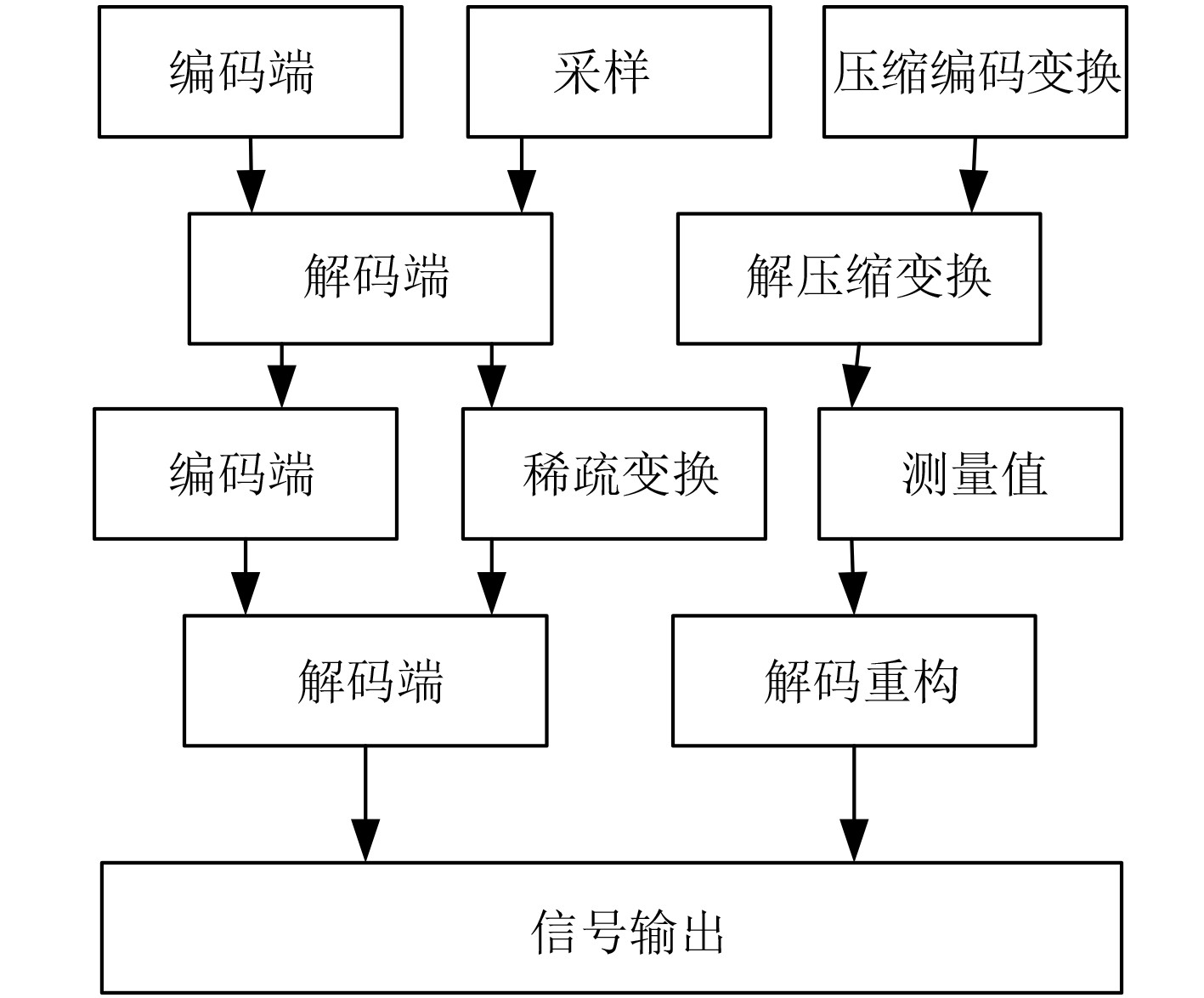
1 无线网络的船舶监控中心多源定位方法 1.1 基于压缩感知的多源数据收集在无线网络中,需要通过一跳或者多跳方式传输数据,这个过程中受到数据量大、节点能耗不均等原因导致能量消耗较大,为减少网络中的数据量,降低节点消耗,在采集数据的基础上,采用压缩感知理论压缩数据[3]。整个过程如图1所示。
|
图 1 基于压缩感知的采样过程 Fig. 1 Sampling process based on compressed sensing |
为确保在模拟信号的采集过程中不发生畸变,必须保证采样频率比模拟信号的峰值频率高1倍以上。在此基础上,采集数据,假定节点每秒会产生一个数据包,将数据包长度设定为
|
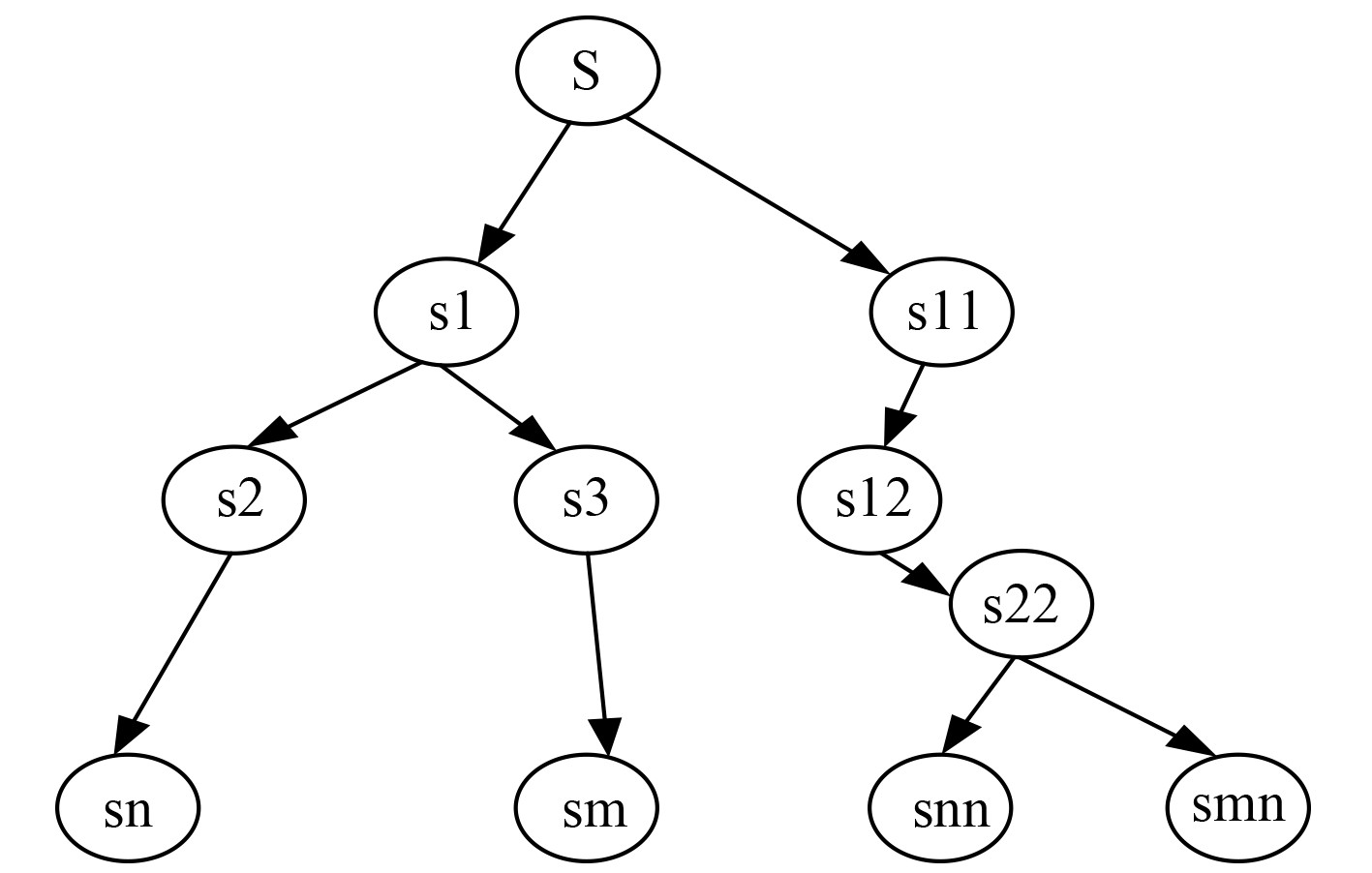
图 2 数据传递模型 Fig. 2 Data transfer model |
采用最小生成树进行数据传递,在数据收集过程中采用多对一的特征对数据传递,父节点会接收到子节点数据传输的信息,采用数据压缩技术压缩,将压缩公式表示为:
| $ {C_{ij}} = {\beta _1} + {\beta _2}D_{ij}^\alpha 。$ | (1) |
式中:
经过压缩后向sink转发[4],减少转发的数据量。为了保证整个过程是连续的,要保证每个节点能量是足够的,为此需要补充能量[5],将能量补充周期表示为:
| $ \tau ={\tau }_{P}+{\tau }_{vac}+\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\tau }_{k} 。$ | (2) |
式中:
采用D-S证据理论算法对数据融合,核心思想是证据组合规则,能够组合从不同信息源上采集得到的信息,使融合结果更加可靠、准确。预先对采集的信息预处理,求出各个证据数据的基本概率赋值
| $ m(\text{Θ})=0,\underset{A\subset \text{Θ}}{{{\displaystyle \sum }}^{\text{}}}m(A)=1 。$ | (3) |
式中:
将
| $ Bel(A)=\underset{B\subseteq A}{{{\displaystyle \sum }}^{\text{}}}m(B)Pl(A)=\underset{A{{\displaystyle \cap }}^{\text{}}B\ne \text{Φ}}{{{\displaystyle \sum }}^{\text{}}}m(B) ,$ | (4) |
式中,
采用D-S证据理论中的合成规则[8],融合证据,公式表示为:
| $ \left\{\begin{array}{l}m(A)=\dfrac{\underset{{A}_{i}{{\displaystyle \cap }}^{\text{}}{B}_{j}{{\displaystyle \cap }}^{\text{}}{C}_{i}=A(i\ne j)}{{{\displaystyle \sum }}^{\text{}}}{m}_{1}\left({A}_{i}\right){m}_{2}\left({B}_{j}\right){m}_{3}\left({C}_{l}\right)}{1-k},\\ m(\text{Φ})=0 。\end{array} \right.$ | (5) |
式中:m1,m2,m3分别代表冲突因子;Ai,Bj,Cl分别代表第i个、第j个、第l个数据的上限函数;
在船舶监控中心多源定位中,存在时间漂移和时间延迟的不确定性,在长时间监控中,会受到间隔时间不确定性的影响,为此需要对发送节点与接收节点之间的时间表转换[9],步骤如下:
1)转换接收点的时间信标与实际时间[10],计算公式表示为:
| $ \rho (t) = f(t) - 1,$ | (6) |
式中,f(t)代表实际时刻
2)把传输节点的时间变换成真实的时间,任何一个节点的本地时钟读数表示为:
| $ {C}_{i}(t)=\frac{1}{{f}_{0}}{{{\displaystyle \int }}^{\text{}}}_{{t}_{0}}^{t}f(t){\rm{d}}t+{C}_{i}\left({t}_{0}\right) 。$ | (7) |
式中:f0代表结点晶体振荡额定频率;t0代表目前的实际时间;Ci代表第i个时刻节点的时钟读数。
3)测量数据的距离,重构信号测量值为:
| $ \left[ {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ \vdots \\ {{y_M}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\varphi _{11}}}&{{\varphi _{12}}}& \cdots &{{\varphi _{1N}}} \\ {{\varphi _{21}}}&{{\varphi _{22}}}& \cdots &{{\varphi _{2N}}} \\ \vdots &{}& \vdots &{} \\ {{\varphi _{M1}}}&{{\varphi _{M2}}}& \cdots &{{\varphi _{MN}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{d_1}} \\ {{d_2}} \\ \vdots \\ {{d_N}} \end{array}} \right] 。$ | (8) |
式中:
4)由于在多跳路径上,时间戳每经过一跳都会得到更新,因此在转换过程中只能够得到一个上下界限值,即偏差范围会扩大,推导出下述公式:
| $ 1 - {\rho _{\max }} \leqslant \frac{{{{\Delta }}h}}{{{{\Delta }}t}} \leqslant 1 + {\rho _{\max }} 。$ | (9) |
式中:
5)消息传输延迟估计,公式表示为:
| $ {D_s}{\text{ = }}\left( {h\left( t \right) - {h_r}\left( t \right)} \right)\frac{{1 - {\rho _s}}}{{1 + {\rho _r}}} 。$ | (10) |
式中:h(t),hr(t)分别代表携带的信息;ρs,ρr分别代表发送节点与接收节点的时钟漂移值。
在实际场景中,一些节点通信情况较少,时间漂移情况会加大,导致估计的时间延迟值估计结果不准确,针对这种情况发送一个空白消息,缓解该问题。
1.3 船舶监控中心多源定位实现移动节点实时发送自己坐标信息给邻居节点,邻居节点接收到移动节点的位置坐标信息,经过时间转换后,调整位置坐标。而未知节点接收到的信息来自不同位置的移动节点,所以对于自身位置坐标节点的计算精确度也不同,未知节点与移动节点的方程组表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2} + {{\left( {{z_1} - z} \right)}^2} = d_1^2} ,\\ {{{\left( {{x_2} - x} \right)}^2} + {{\left( {{y_2} - y} \right)}^2} + {{\left( {{z_2} - z} \right)}^2} = d_2^2},\\ \vdots \\ {{{\left( {{x_n} - x} \right)}^2} + {{\left( {{y_n} - y} \right)}^2} + {{\left( {{z_n} - z} \right)}^2} = d_n^2} ,\end{array}} \right. $ | (11) |
式中,(x,y,z)代表未知节点坐标。
将上述方程组转换为矩阵乘法,做如下处理:
| $ {\boldsymbol{A}} * {\boldsymbol{B}} = \left( {\begin{array}{*{20}{c}} {{x_1} - {x_n}}&{{y_1} - {y_n}}&{{z_1} - {z_n}} \\ {{x_2} - {x_n}}&{{y_2} - {y_n}}&{{z_2} - {z_n}} \\ \vdots & \vdots & \vdots \\ {{x_{n - 1}} - {x_n}}&{{y_{n - 1}} - {y_n}}&{{z_{n - 1}} - {z_n}} \end{array}} \right) ,$ | (12) |
求解齐次方程,公式如下:
| $ {\boldsymbol{X}} = {\left( {{{\boldsymbol{A}}^\prime }{\boldsymbol{A}}} \right)^{ - 1}} * {{\boldsymbol{A}}^\prime }{\boldsymbol{B}} 。$ | (13) |
经过上述计算,求得初始坐标,同时,节点移动是一个连续的过程,后续不同位置的移动节点信息对未知节点定位的影响会不同,为此将多源定位数据问题转换为连续性后验概率计算问题。预先设置数据的初始坐标,将其记作
| $ x_m^c(t) = \cos {\theta _m} * dis + x_m^c(t - 1) 。$ | (14) |
式中:
在计算过程中,每个未知节点接收到节点广播的数据包,采用后验概率公式,实时调整自己坐标,后验概率公式为:
| $ p = p\left( {\left( {x_m^c(t),y_m^c(t)} \right)} \right) * p\left( {\left( {{x_u}(t),{y_u}(t)} \right)\mid \left( {{x_m},{y_m}} \right)} \right) 。$ | (15) |
式中:
经过上述过程不断迭代,实现船舶监控中心多源数据定位。
2 实验结果与对比为验证船舶监控中心多源数据定位方法的有效性,将基于高斯滤波的算法、基于布谷鸟算法的定位算法与本文方法进行对比实验。利用模拟工具,在10 m×10 m×10 m的环境中,在该区域中任意分布位置节点,该节点之间的通信半径为5 m,该节点可以与其他锚点进行直接通信。实验共分为2部分,第一部分采用3种方法对数据点测距,第二部分对比不同迭代次数下的定位误差,第三部分对比3个方法在不同锚节点下定位的平均总误差。3种测距误差对比结果如表1所示。可知,本文定位方法最大的测距误差为0.03 m,另2种方法的定位误差基本都在0.11左右,测距误差较大,没有本文方法的测距效果好。
|
|
表 1 测距误差对比 Tab.1 Comparison of ranging errors |
定位误差的计算公式为:
| $ {e_i} = \sqrt {{{\left( {{x_{ie}} - {x_{it}}} \right)}^2} + {{\left( {{y_{ie}} - {y_{it}}} \right)}^2} + {{\left( {{z_{ie}} - {z_{it}}} \right)}^2}} 。$ | (16) |
式中:
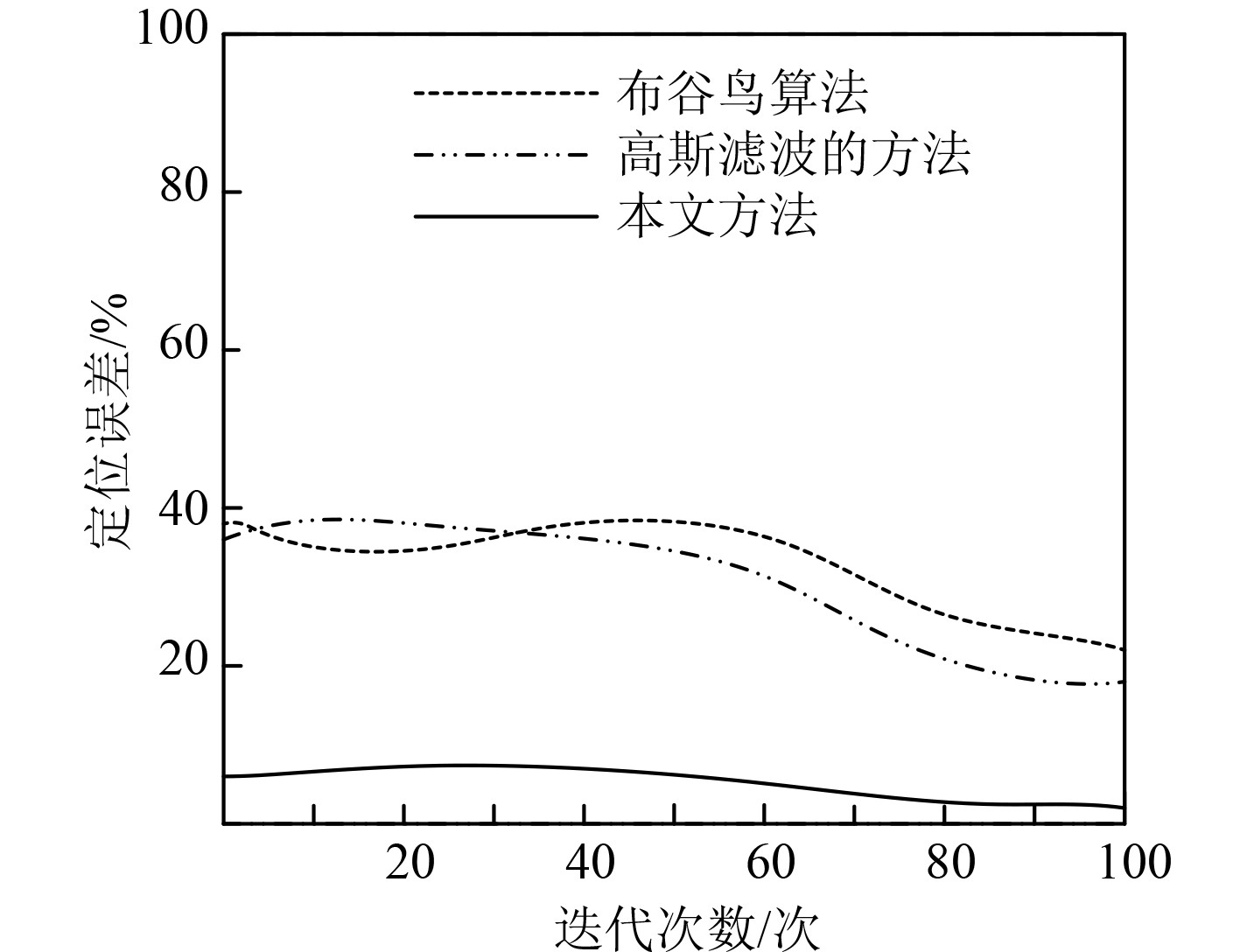
3个方法在不同迭代次数下的定位误差对比结果如图3所示。可知,随着迭代次数的增加,3种方法的定位误差都在逐渐降低,本文方法节点定位误差较低,较另2种方法定位准确度都高。本文方法获得较好的定位效果的原因是,所提出方法预先对定位数据采集与整理,并对数据采集的时间进行了转换,从而降低了数据定位的误差。
|
图 3 不同迭代次数下定位误差 Fig. 3 Node positioning error |
进行不同锚节点数量下的定位实验,通过模拟软件,可以产生100 m×100 m×100 m的网络节点,在给定的区域中,随机配置100个节点,使锚点能覆盖到整个网络的50%。节点分布如图4所示,基本的参数如表2所示。
|
|
表 2 实验参数 Tab.2 Experimental parameters |
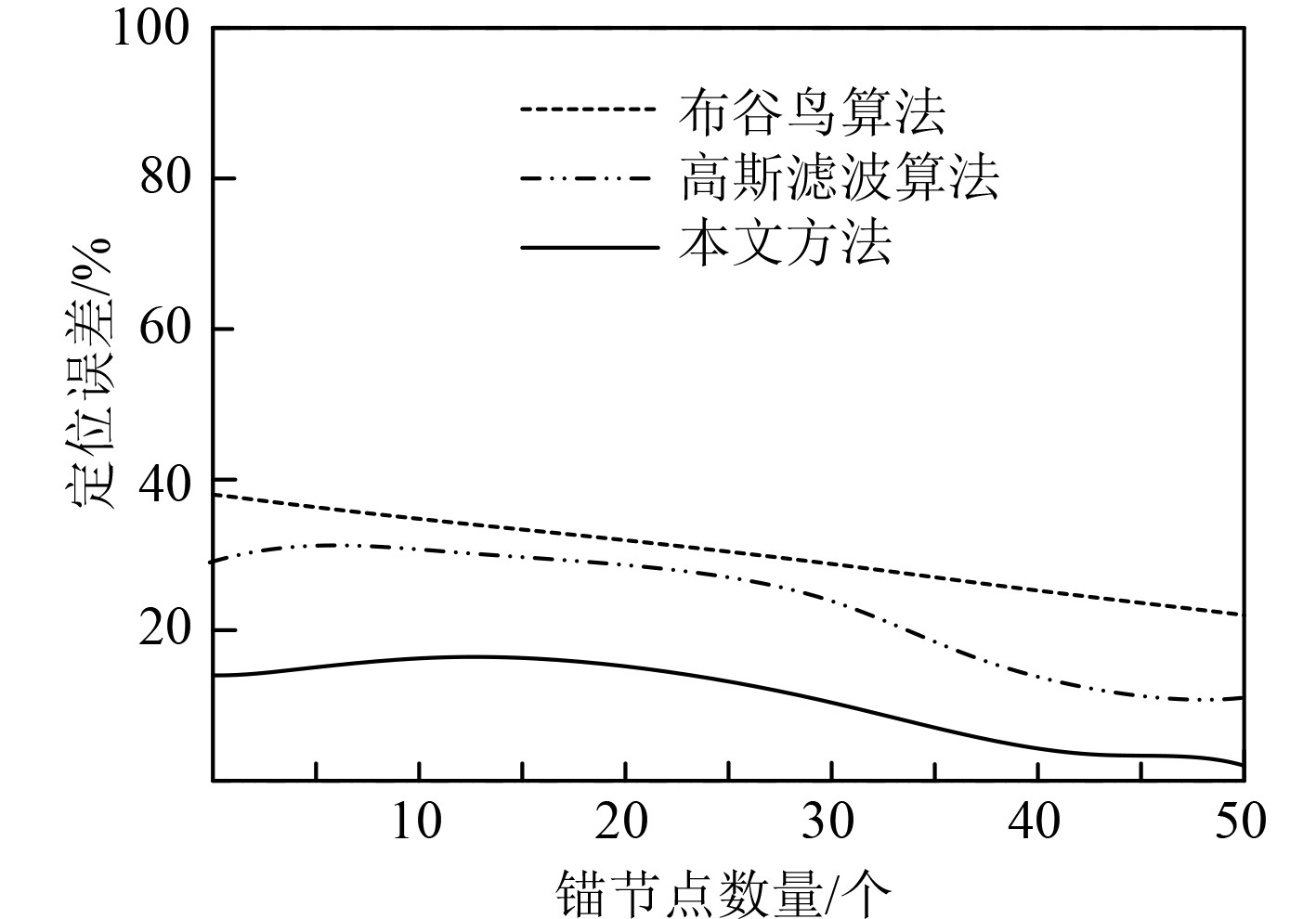
3个方法在不同锚节点数量下的定位误差对比结果如图5所示。可知,随着锚节点数量的增加,3种方法的定位误差逐渐减小,在锚节点数量为20个时,本文方法误差趋于稳定。另2个方法的定位误差虽然有逐渐降低的趋势,但是误差仍然高于本文方法。

|
图 4 节点分布图 Fig. 4 Node distribution diagram |
|
图 5 不同锚节点数量下定位误差对比 Fig. 5 Comparison of positioning errors with different anchor node numbers |
本文设计了无线网络的船舶监控中心多源定位数据方法,实验结果表明所研究的方法有效提高了定位的准确性。
| [1] |
王磊, 刘利利, 齐俊艳, 等. 基于高斯滤波的三维水声无线传感网络节点定位算法[J]. 河南理工大学学报:自然科学版, 2021, 40(4): 147-153. |
| [2] |
李娜, 贾伟. 布谷鸟算法在无线传感器网络中的定位研究[J]. 数据采集与处理, 2020, 35(2): 315-321. |
| [3] |
陈暄, 顾锦, 毛科技, 等. 一种改进鲸鱼算法的无线传感器网络定位优化研究[J]. 传感技术学报, 2021, 34(10): 1366-1373. |
| [4] |
田圳, 李丛林, 王伟力, 等. 基于多源监控数据的设备状态感知方法[J]. 电力系统及其自动化学报, 2020, 32(7): 145-150. |
| [5] |
刘期烈, 万志鹏, 周文敏, 等. 一种改进的多源信息融合室内定位方法[J]. 电讯技术, 2021, 61(12): 1526-1533. DOI:10.3969/j.issn.1001-893x.2021.12.010 |
| [6] |
刘宇, 惠鸿飞, 路永乐, 等. 基于遗传算法优化神经网络的多源信息融合室内定位方法[J]. 中国惯性技术学报, 2020, v.28(01): 73-79. |
| [7] |
石兆军, 周晓俊, 李可, 等. 基于多源信息融合的网络安全监控技术[J]. 计算机工程与设计, 2020, 41(12): 3361-3367. |
| [8] |
胡正平, 张乐, 李淑芳, 等. 端对端SSD实时视频监控异常目标检测与定位算法[J]. 燕山大学学报, 2020, 44(5): 493-501. DOI:10.3969/j.issn.1007-791X.2020.05.010 |
| [9] |
张俊豪, 罗国富, 杨幸博, 等. 基于深度学习和机器视觉的多源数据感知技术研究[J]. 河南理工大学学报:自然科学版, 2021, 40(4): 107-113. |
| [10] |
高美凤, 尹持俊. 基于UAV的无线传感器网络加权质心定位算法[J]. 传感技术学报, 2021, 34(4): 539-545. DOI:10.3969/j.issn.1004-1699.2021.04.016 |
 2022, Vol. 44
2022, Vol. 44
