0 引　言

随着遥感技术的不断完善及其升级，获得的遥感图像也逐渐向高清晰分辨度方向发展，其应用范围也在逐渐扩张，尤其是海洋领域^[1]。由于海上环境的多变，很难对目标进行精确的探测，不但威胁着海上船舶的安全性，也为海上航运事业的发展带来了一定的制约影响^[2]。就已有研究成果来看，由于应用技术的落后，无法精准地识别船舶目标，因此提出卷积神经网络的船舶遥感图像目标检测方法研究。

1 卷积神经网络船舶遥感图像目标检测方法 1.1 船舶遥感图像增强处理

遥感图像具有信息量复杂、图像覆盖范围大、存储信息庞大、目标干扰因素多等特点，加之船舶目标颜色与海洋表面较为接近，使得船舶目标检测困难较大。为了方便后续船舶目标特征提取，采用拉普拉斯算子增强处理船舶遥感图像^[3]。将遥感图像定义为三维函数f(x,y,z)，其中，(x,y)代表遥感图像中的某一个点，a代表(x,y)像素的维度数值。拉普拉斯算子表达式为：

$ {\nabla ^2}f = \frac{{{\partial ^2}f}}{{\partial {x^2}}} + \frac{{{\partial ^2}f}}{{\partial {y^2}}} 。$

(1)

拉普拉斯算子呈现为线性特征，在 $ x $ 方向及其 $ y $ 方向将其转换为差分形式，将差分形式代入式(1)，即可获得更加精确的拉普拉斯算子，表达式为：

$ \begin{aligned} & {\nabla }^{2}f=f\left(x,y+1\right)+f\left(x,y-1\right)+\\ & f\left(x+1,y\right)+f\left(x-1,y\right)-4f\left(x,y\right)。\end{aligned}$

(2)

依据式(2)即可获得滤波模板，有效结合拉普拉斯算子，最终获得拉普拉斯滤波，表达式为：

$ g\left( {x,y} \right) = f\left( {x,y} \right) + \alpha \left[ {{\nabla ^2}f\left( {x,y} \right)} \right] 。$

(3)

式中， $ \alpha $ 为拉普拉斯算子的辅助因子。

应用拉普拉斯滤波，对船舶遥感图像进行增强处理，如图1所示。

由图1可知，在船舶遥感图像增强后，遥感图像中依然存在着大量的噪声点，这些噪声点的存在会极大影响船舶目标检测的精度。经过分析可知，遥感技术应用过程中，遥感设备容易受到脉冲噪声的干扰，从而致使遥感图像中包含较多的噪声点，降低遥感图像的质量。为了消除噪声点的不利影响，利用中值滤波处理增强后的遥感图像。中值滤波表达式为：

$ g'\left( {x,y} \right) = {\rm{med}}\left\{ {g\left( {x - k,y - l} \right),\left( {k,l} \right) \in W} \right\} 。$

(4)

式中： $ g'\left( {x,y} \right) $ 为经过中值滤波处理后的遥感图像；med{}为取中值函数表达式；W为卷积核规模大小；(k,l)为中值滤波每次移动步长大小数值^[4]。

1.2 船舶遥感图像目标特征提取

以增强处理后的船舶遥感图像为基础，基于Snake模型分割出遥感图像中的船舶目标，采用Gabor滤波器提取船舶遥感图像目标特征，为后续船舶目标检测提供直接依据^[5]。在Snake模型应用过程中，依据遥感图像船舶目标分割需求初始化活动轮廓线，以能量泛函为依据，通过不断演化对船舶目标边缘轮廓进行逼近，直到能量泛函达到最小值为止，输出结果即为遥感图像船舶目标分割结果^[6]。Snake模型能量泛函表达式为：

$ \left\{ {\begin{array}{*{20}{c}} {{E_{Snake}} = \displaystyle\int\nolimits_0^1 {{E_{{int} }}\left( {v\left( s \right)} \right) + {E_{ext}}\left( {v\left( s \right)} \right){\rm{d}}s} } ，\\ {{E_{{int} }}\left( {v\left( s \right)} \right) = \lambda \left( s \right){{\left| {v'\left( s \right)} \right|}^2} + \zeta \left( s \right){{\left| {v''\left( s \right)} \right|}^2}} 。\end{array}} \right. $

(5)

式中：E_snake为Snake模型的能量泛函；Ei_nt(v(s))与E_ext(v(s))分别为活动轮廓线的内部约束力与外部约束力； $ v\left( s \right) $ ， $ v'\left( s \right) $ 与 $ v''\left( s \right) $ 分别为控制弹性系数及其1阶与2阶导数； $ \lambda \left( s \right) $ 与 $ \zeta \left( s \right) $ 为归一化弧长参数。

当E_snake达到最小值时，活动轮廓线在内部约束力与外部约束力的作用下，逐渐逼近船舶目标轮廓，最终使两者基本重合，即可实现船舶目标的分割。

以分割后遥感图像船舶目标为基础，应用Gabor滤波器提取船舶遥感图像目标特征^[7]。Gabor滤波器能够对船舶目标进行Gabor变换，变换后遥感图像梯度更加明显，边缘更加突出，为船舶目标特征向量提取提供极大便利。另外，Gabor滤波器不会受到光照信息的影响，对不同光照遥感图像具有同样的应用效果，充分证实了Gabor滤波器具备强大的适应性^[8]。

常规情况下，Gabor变换后遥感图像变为灰度图像，信息量呈现急剧减少的趋势，船舶目标轮廓、纹理等信息变得突出，有效地滤除了干扰信息，如光照信息、颜色信息等，有助于船舶目标特征向量的提取^[9]。基于Gabor滤波器提取船舶目标特征，具体步骤如下：

1) Gabor变换处理遥感图像，获取Gabor核对应数量的纹理图像；

2) 依据步骤一获得Gabor纹理图像生成特征向量。特征向量由响应矩阵元素绝对值和及其平方和顺序排列构成。响应矩阵元素绝对值和及其平方和计算公式为：

$ \left\{ {\begin{array}{*{20}{c}} {\beta = \sum\limits_i {\sum\limits_j {\left| {{n_{ij}}} \right|} } }，\\ {\chi = \sum\limits_i {\sum\limits_j {{n_{ij}}^2} } } 。\end{array}} \right. $

(6)

式中： $ \beta $ 与 $ \chi $ 分别为响应矩阵元素绝对值和及其平方和； $ {n_{ij}} $ 为坐标为 $ \left( {i,j} \right) $ 的元素数值。

3) 标准化处理Gabor特征向量。每个特征向量取值范围、量纲均存在着差异，无法对其进行直接应用，故对其进行标准化处理，消除差异化影响^[10]。标准化处理公式为：

$ {n'_{ij}} = \frac{{{n_{ij}} - \delta }}{\sigma }。$

(7)

式中： $ {n'_{ij}} $ 与 $ {n_{ij}} $ 分别为标准化处理后、前的特征向量元素； $ \delta $ 与 $ \sigma $ 分别为特征向量元素的均值与标准差。

完成船舶遥感图像目标的分割与特征提取后，为后续船舶遥感图像目标检测的实现做好充足的数据准备^[11]。

1.3 船舶遥感图像目标检测实现

以提取的船舶遥感图像目标特征为依据，基于卷积神经网络搭建船舶遥感图像目标检测架构，对卷积神经网络进行训练，获取最优权重系数。将遥感图像输入至训练好的卷积神经网络中，即可实现船舶目标的检测^[12]。船舶遥感图像目标检测架构如图2所示。可知，搭建船舶遥感图像目标检测架构包含双分支卷积神经网络，从2个方向增强船舶目标的特征，并对其进行有效提取，从而提升目标检测方法的整体性能^[13]。

其中，显著性重建分支网络主要是通过模拟人类视觉感知系统，对遥感图像中的显著性区域进行精准定位。而显著性区域即为覆盖船舶目标区域，不但能够引导检测分支网络关注到船舶目标区域，也能抑制非显著性区域冗余信息的干扰。由此可见，显著性重建分支网络是船舶目标检测架构中必不可少的部分^[14]。

另外，显著性重建分支网络可以有效的优化显著性信息提取方式，是能够有效降低卷积神经网络的迭代次数，提升船舶目标检测的效率^[15]。

在卷积神经网络应用过程中，为了保障显著性重建分支网络与检测分支网络的一致性，获得更精准的船舶目标检测结果，对2分支网络置信度进行统一化处理，表达式为：

$ \kappa = \frac{{{e^{{p_i}\left( k \right)}}}}{{{e^{{p_i}\left( 1 \right)}} + {e^{{p_i}\left( 2 \right)}}}} 。$

(8)

式中： $ \kappa $ 为统一化处理后的卷积神经网络置信度； $ {e^{{p_i}\left( k \right)}} $ 为第 $ i $ 像素对应的像素值； $ {e^{{p_i}\left( 1 \right)}} $ 与 $ {e^{{p_i}\left( 2 \right)}} $ 分别为显著性重建分支网络与检测分支网络输出像素值。

由图2可知，卷积神经网络训练过程是在像素级、目标级损失函数的共同约束下进行的，能够提升卷积神经网络训练的准确性，为船舶目标检测提供最佳的卷积神经网络支撑。两级损失函数确定对船舶目标检测具有至关重要的作用，其表达式为：

$ L = \gamma {L_p} + {L_b} 。$

(9)

式中： $ L $ 为两级损失函数；L_p与L_b分别为像素级、目标级损失函数； $ \gamma $ 为权重系数。

通过循环迭代训练即可确定最优权重系数，将待检测遥感图像输入至卷积神经网络中，即可获得船舶目标检测结果。

2 实验与结果分析

设计实验验证本文方法的应用性能。在实验准备阶段完成实验数据的准备与卷积神经网络最优权重系数的确定，为后续实验顺利进行提供支撑。随机选取150幅遥感图像作为实验数据，设置训练集合遥感图像数量为50幅，测试集合遥感图像数量为100幅。部分实验数据如图3所示。

权重系数直接关系着船舶目标检测的精度。通过训练获取权重系数与目标检测精度之间的关系曲线，如图4所示。可知，当权重系数为0.26时，获得船舶目标检测精度最高，因此确定最优权重系数为0.26。

选取F1 Score参量与IoU参量作为评价指标，F1 Score参量可以反映船舶目标检测的精度，IoU参量能够有效反映船舶目标检测定位的准确性。F1 Score参量与IoU参量计算公式为：

$ \left\{ {\begin{array}{*{20}{c}} {F1Score = \dfrac{{2 \times precision \times recall}}{{precision + recall}}} ，\\ {IoU = \dfrac{{{S_{{int} er\sec tion}}}}{{{S_{union}}}}} 。\end{array}} \right. $

(10)

式中：precision与recall分别为船舶目标检测的精准率与查全率；S_intersection与S_union分别为预测框与真实目标框。

通过实验获得F1 Score参量数据如表1所示。可知，应用本文方法获得的F1 Score参量数值均高于标准数值，表明本文方法船舶目标检测精度较高。

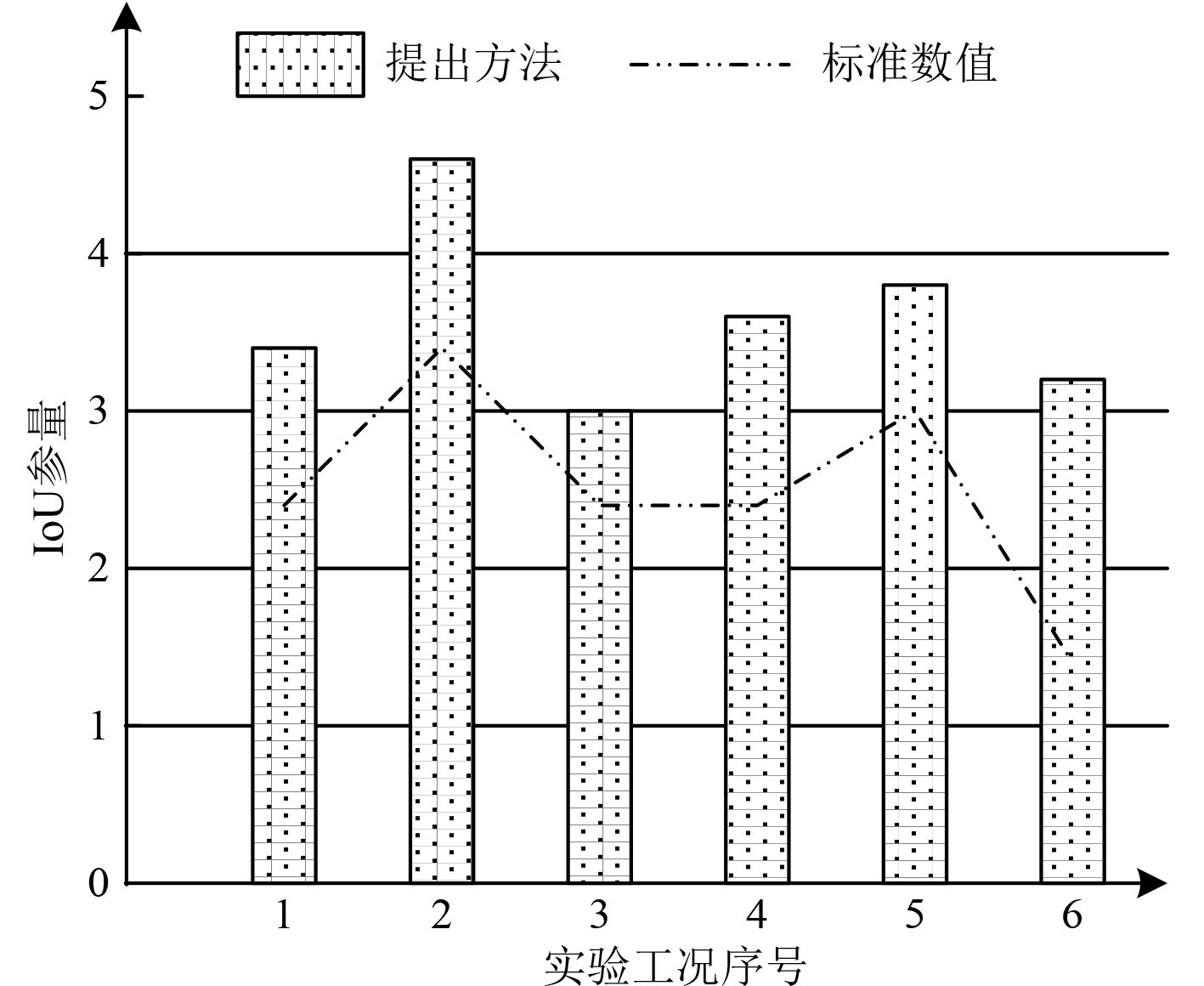
通过实验获得IoU参量数据如图5所示。可知，应用本文方法获得的IoU参量数值均高于标准数值，表明本文方法船舶目标检测定位准确性较高。

实验数据表明：相较于给定标准数值来看，应用本文方法获得的F1 Score参量与IoU参量数值较大，充分证明本文方法船舶目标检测效果较好。

3 结　语

本文引入卷积神经网络设计了新的船舶遥感图像目标检测方法，极大提升了F1 Score参量与IoU参量数值，可以更好检测船舶目标，为目标检测相关研究提供一定的参考。