2. 江苏科技大学 计算机学院,江苏 镇江 212000
2. School of Computer Science, Jiangsu University of Science and Technology, Zhenjiang 212000, China
在声呐信号采集和传输的过程中,数字信号经常被各种噪声所污染,且海洋环境复杂多变,混合的声音信号使声呐图像不同于光学图像。针对声呐图像分辨率低、背景噪声高、边缘对比度差及缺少有用信息等特性,结合光学图像的研究成果,提出了一些去噪增强理论和算法,包括线性与非线性函数[1]、多尺度retinex[2]、形态学方法[3]等,由于声呐图像本质与光学图像有很大的差别,因此对声呐图像处理的应用受到限制,效果也并不理想。从20世纪末开始发展起来的多分辨率分析理论,例如傅里叶变换[4]、小波变换[5]、Ridgelet变换[6]和Curvelet变换[7],为处理信号奇异性提供强大的分析工具。近年来,小波在声呐图像降噪和识别中取得了一定的成功,由于小波的局限性,并不能有效地解决线奇异性和有限的方向选择性。为了克服这些缺点,Donoho等[8]提出一种新的图像表示方法Ridgelet,可以有效处理线或超平面奇点并以足够精细的比例以局部方式分析曲线。Da C等[9]以Contourlet 变换为基础进行改进提出了具有多尺度、多方向和平移不变性的非下采样Contourlet变换(NSCT),使用非下采样拉普拉斯金字塔(LP)和方向滤波器组(DFB)构造分解结构。该过程可以避免下采样过程,从而使变换具有平移不变性,并进一步提高Contourlet变换在图像去噪领域的性能。基于传统贝叶斯原理的NSCT系数方差估计算法存在一个问题,即如何选择合适的原始图像先验概率系数模型和噪声系数[10-11]。为了解决此问题,可以使用变贝叶斯方法。V-Bayes的基本思想[12]是用更容易近似的分布近似真实的后验概率,通过最小化近似分布和实际后验概率分布之间的Kullback-Leibler Divergence(KL散度)[13]差异来预测估计。
本文结合NSCT二元模型和V-Bayes估计,提出了一种图像去噪算法,对声呐图像进行了仿真分析,并与现有的经典方法进行了比较。结果表明,该算法可以有效去除图像中的噪声,获得最高的PSNR值和噪声抑制能力。
1 相关介绍 1.1 非下采样轮廓波NSCTContourtlet变换可以以最佳方式稀疏地表示图像,并且能有效捕获和刻画图像中弯曲和定向的几何结构,其结构中LP和DFB都进行了下采样操作,因此Contourtlet系数的冗余大大降低,以至于Contourlet 变换缺少平移不变性,使增强后的图像在不连续的点边缘产生伪“Gibbs”现象。为了解决上述问题,NSCT舍弃了Contourtlet变换中的下采样操作,将非下采样金字塔(NSP)和非下采样方向滤波器组(NSDFB)组合,在采样的比例上与原始图像比例相同。
NSP可确保NSCT的多尺度特性,NSP分解阶段生成2个子带:低频子带和高频子带,利用NSDFB对高频子带进行方向分析,从各个方向展示图像的轮廓细节和边缘特征。NSP对图像进行n级尺度分解,可得到n+1个子带图像。图1为2层NSCT变换的原理图。

|
图 1 NSCT分解原理图 Fig. 1 NSCT decomposition schematic |
小波变换系数存在一定程度的相关性,其中,双变量模型充分利用了图像小波系数的尺度相关性,使用非高斯密度函数对“父”和“子”系数的分布进行建模,并使用贝叶斯统计理论获得解析表达式最大后验估计。
NSCT分解相邻尺度之间的各级系数有很强的相关性,即NSCT变换域中的系数具有与小波系数相似的分布特性。因此,小波域中的双变量模型的处理思想可用于将其扩展到NSCT变换域中。
为了估计NSCT系数复方差
| $ y = w + n, $ | (1) |
其中
在NSCT域,根据贝叶斯最大后验估计(MAP),从
| $ \hat w(y) = {\rm{argmax}}[{\rm{log}}({p_n}(y{\text{ - }}w)) + {\rm{log}}({p_n}(w))]。$ | (2) |
上面的方程式中,首先必须知道噪声的NSCT分解系数的概率分布。在此假设噪声密度函数
| $ {p_n}(n) = \frac{1}{{2{\text{π}} \sigma _n^2}}{\rm{exp}}\left( - \frac{{n_1^2 + n_2^2}}{{2\sigma _n^2}}\right) 。$ | (3) |
Sendur等提出双变量模型对小波上下级系数进行描述,NSCT内系数概率分布用联合概率密度函数
| $ {p_w}(w) = \frac{3}{{2{\text{π}} {\sigma ^2}}}{\rm{exp}}( - \frac{{\sqrt 3 }}{\sigma }\sqrt {w_1^2 + w_2^2} ), $ | (4) |
式中:
| $ {\hat w_1} = \frac{{\left(\sqrt {y_1^2 + y_2^2} - \dfrac{{\sqrt 3 \sigma _n^2}}{\sigma }\right)}}{{\sqrt {y_1^2 + y_2^2} }} + {y_1} 。$ | (5) |
式(5)是双变量模型中当前系数
MAP估计方法不需要显示求出后的后验密度函数,只要得出最大概率密度的点值,属于点估计范畴,对模型参数没有给出一个很好的估计准则,而变分贝叶斯方法是对整个后验密度的求解,因此可以利用更多的信息.为了解决传统贝叶斯估计问题,变分贝叶斯方法提供了有效的解决方案。
对给定的原始图像w,噪声图像y,根据贝叶斯定理:
| $ p\left( {\nabla \left. w \right|\nabla y} \right) = \frac{{p\left( {\nabla \left. y \right|\nabla w} \right)p\left( {\nabla w} \right)}}{{p\left( {\nabla y} \right)}}。$ | (6) |
其中:
用易于处理的近似分布q(
| $ \begin{split} &KL\left\{q(\nabla w,{\sigma }^{2})\Vert p(\nabla w|\nabla y)\right\}=\\ &\qquad \int q(\nabla w,{\sigma }^{2})\mathrm{ln}\dfrac{q(\nabla w,{\sigma }^{2})}{p(\nabla w|\nabla y)}{\rm{d}}\nabla w+\mathrm{ln}p(\nabla y)\geqslant 0,\end{split} $ | (7) |
当且仅当q(
| $ \begin{split} {C}_{KL}=&KL\{q(\nabla w,{\sigma }^{2})\Vert p(\nabla w|\nabla y)\}-\mathrm{ln}p(\nabla y)=\\ & \int q(\nabla w,{\sigma }^{2})\mathrm{ln}\dfrac{q(\nabla w,{\sigma }^{2})}{p(\nabla w|\nabla y)}{\rm{d}}\nabla w+\\ & \int q(-{\sigma }^{2})\mathrm{ln}\dfrac{q(-{\sigma }^{2})}{p(-{\sigma }^{2})}{\rm{d}}(-{\sigma }^{2})。\end{split} $ | (8) |
贝叶斯变化估计通过迭代方法(即贝叶斯期望最大化定理)使成本函数最小,从而估计噪声函数。使用变分贝叶斯方法进行噪声参数估计,特点在于可以求出后验密度分布的逼近分布,存在闭合形式的解,可以更好地估计后续的高频子带噪声参数。
2 模糊对比度增强NSCT分解后,其低频子带具有
| $ X = \mathop \bigcup \limits_{m = 1}^M \mathop \bigcup \limits_{n = 1}^N \frac{{{u_{mn}}}}{{{x_{mn}}}} ,$ | (9) |
模糊集的隶属度函数将低频带图像映射到模糊特征平面,从而使图像特征更容易识别和提取。采用一种改进的正余弦结合模糊隶属函数:
| $ {u_{mn}} = \frac{1}{2}\left[{\rm{sin}}\left(\frac{{\text{π} ({x_{mn}} - {x_{{\rm{min}}}})}}{{2({x_{{\rm{max}}}} - {x_{{\rm{min}}}})}}\right) - {\rm{cos}}\left(\frac{{\text{π} ({x_{mn}} - {x_{{\rm{min}}}})}}{{2({x_{{\rm{max}}}} - {x_{{\rm{min}}}})}}\right) + 1\right] 。$ | (10) |
改进的隶属度函数曲线为“S”型,符合模糊理论对隶属度函数凹凸性的要求,且具有效果较好的去噪性。
运用模糊增强算子正弦函数的回归调用来修正隶属度:
| $ \begin{split} u_{mn}^{'} =& {T^r}\left( {{u_{mn}}} \right) = T\left( {{T^{r - 1}}\left( {{u_{mn}}} \right)} \right) = \\ &\frac{{{\rm{sin}}(\text{π} ({u_{mn}}{{ - }}0.5)) + 1}}{2}。\end{split} $ | (11) |
式中,r=
将图像从模糊域映射到空间域,其逆变换为:
| $ {x_{mn}} = {x_{{\rm{min}}}} + ({x_{{\rm{max}}}} - {x_{{\rm{min}}}})\frac{{{\rm{arcsin}}{{[1 - {{\left( {2{u_{mn}} - 1} \right)}^2}]}^{\sqrt r }}}}{{\text{π}}} 。$ | (12) |
NSCT具有多方向选择性和平移不变性的优点,而双变量模型可以充分利用图像小波系数的尺度间相关性。
步骤1 对噪声图像进行NSCT,可以设置每个尺度上的NSP分解层数和NSDFB分解方向子带数。
步骤2 估算噪声的NSCT系数方差
步骤3 对于每个高频方向子带,使用局部自适应方法来估计每个系数的模型边缘方差,即
步骤4 将
步骤5 建立模糊域特征平面矩阵,将低频分量带入到模糊域中,再利用改进的正余弦结合隶属度函数并对其特征增强,最后模糊逆变换为空间域矩阵。
步骤6 重建去噪的非下采样Contourlet系数矩阵,并执行逆NSCT变换以获得去噪够的图像。
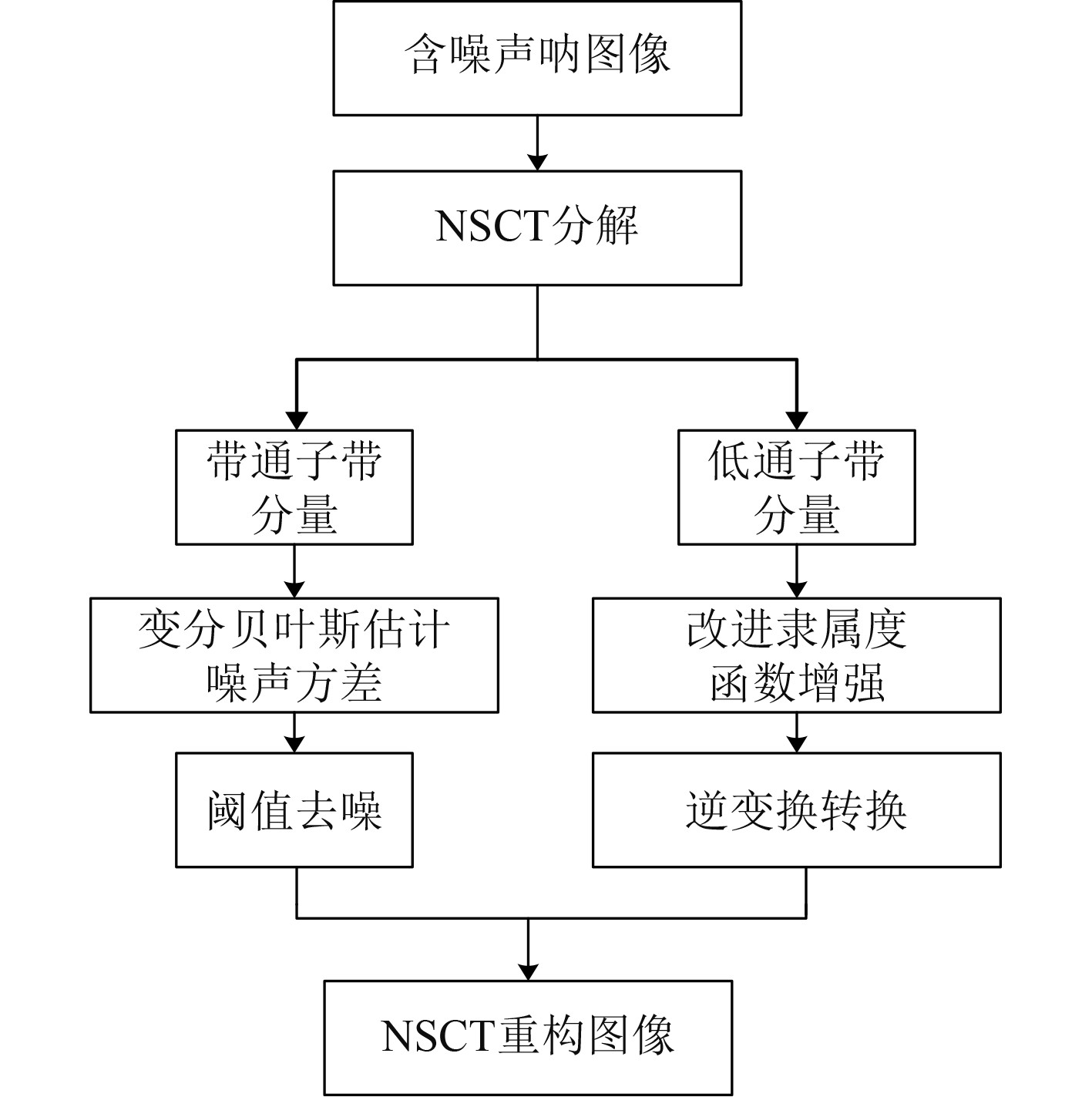
|
图 2 图像增强方法流程图 Fig. 2 The image enhancement method flow chart |
为了演示本文算法的去噪和增强性能,采用Matlab R2019b,计算机内存16 GB,处理器为intel(R)Core(TM)i7,主频为2.2 GHz作为实验环境。选择以灰度等级为512×512像素的声呐图像为测试样本,NSCT分解层数为3层。为了便于比较和分析,该算法与直方图均衡(HE)、离散小波(DWT)、双树复数小波(DTCWT)、非下采样轮廓波(NSCT)进行比较。表1比较了不同方法增强后图像计算信息熵以及峰值信噪比(PSNR)和平均绝对误差(MAE)三项性能指标。
|
|
表 1 五种算法的客观指标 Tab.1 Objective index of five algorithms |
水下恶劣环境下,声呐图像会产生伪Gibbs和目标边缘模糊的现象,图3为对前视声呐图像进行实验结果。
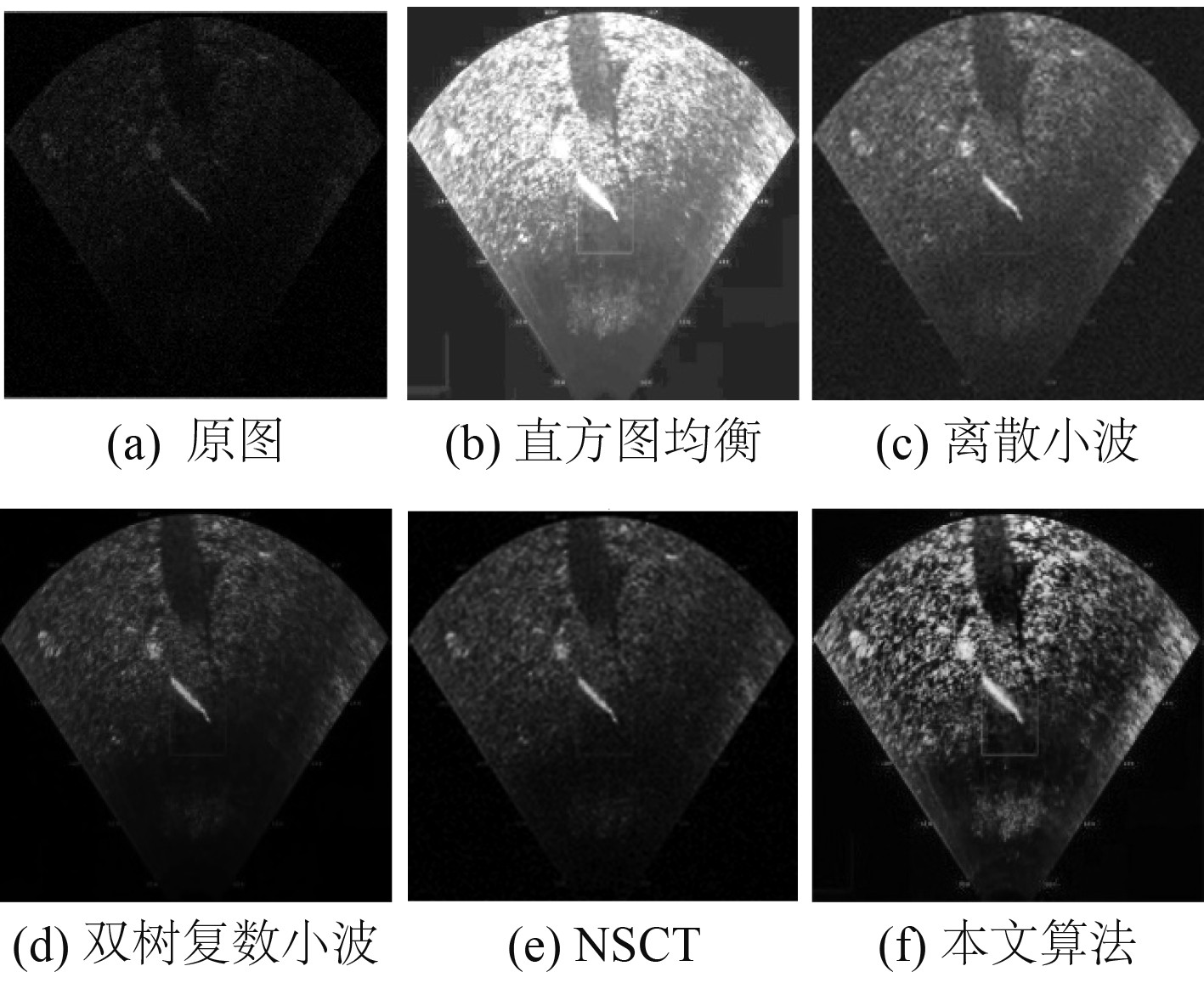
|
图 3 前视声呐图像5种增强方法的结果比较 Fig. 3 Comparison of results of five enhancement methods for forward-looking sonar images |
可以看出,NSCT变换能实现图像的最优稀疏分布逼近,其系数的双变量模型根据信息能量的不同,充分表示了尺度间以及尺度内的尺度相关性,实现变换系数自适应收缩,改进的隶属域函数不仅解决了传统模糊增强中参数因子计算复杂问题,同时采用正余弦结合“S”型函数,低灰度像素值有效保留。实验结果表明,该算法在去除噪声的同时尽可能的保留边缘细节,做到了整体和局部的增强,提高了恢复图像PSNR值,算法的主观视觉效果和客观评价标准都好于对比算法。
4 结 语本文通过对含噪声呐图像进行NSCT分解,并在低频分量和高频分量上分别进行模糊集增强和变分贝叶斯阈值去噪增强。通过在模糊集上构造新的隶属度函数,并改进高频子带阈值自适应取值,使图像的纹理细节突出,图像的边缘更加清晰,对于舰船声呐图像的后续应用有重要意义。
| [1] |
陈鹏, 张建伟. 结合核函数与非线性偏微分方程的图像去噪方法[J]. Computer Science, 2018, 45(11): 278-282. DOI:10.11896/j.issn.1002-137X.2018.11.044 |
| [2] |
WANG Y, WANG H, YIN C, et al. Biologically inspired image enhancement based on Retinex[J]. Neurocomputing, 2016, 177(177): 373-384. |
| [3] |
杨蕴, 李玉, 王玉. 一种数学形态学的量子图像去噪方法[J]. 遥感信息, 2018, 33(2): 17-25. DOI:10.3969/j.issn.1000-3177.2018.02.003 |
| [4] |
李利, 杨恢先, 何雅丽, 等. 结合FT与NSCT的自适应阈值去噪算法[J]. 计算机工程, 2012, 38(17): 238-241. DOI:10.3778/j.issn.1002-8331.2012.17.048 |
| [5] |
姜三平, 郝晓剑. 应用小波系数GSM统计模型的混合傅里叶-小波图像降噪[J]. 中国图象图形学报, 2009, 14(3): 448-451. |
| [6] |
MA Guangsheng, ZHAO Jiman. Quaternion ridgelet transform and curvelet transform. [J].Adoances in Applied Clifford Algebras, 2018, 28(4): 1-21.
|
| [7] |
SHAHDOOSTI H R, HAZAVEI S M. Image denoising in dual contourlet domain using hidden Markov tree models[J]. Digital Signal Processing, 2017, 17-29. |
| [8] |
STARCK J L , CANDES E J , DONOHO D L . The curvelet transform for image denoising[J]. IEEE Transaction on image processing a publication of the IEEE signal processing society, 2002, 11(6): 670-684.
|
| [9] |
DA, C, ARTHUR, et al. The nonsubsampled contourlet transform: theory, design, and applications.[J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089-3101. DOI:10.1109/TIP.2006.877507 |
| [10] |
吴炜, 杨晓敏, 陈默, 等. 基于改进的非下采样Contourlet变换的超分辨率复原算法[J]. 光学学报, 2009, 29(6): 1493-1501. |
| [11] |
HUANG Yun-hu, CHEN De-wang. Image fuzzy enhancement algorithm based on contourlet transform domain[J]. Multimedia Tools and Applications, 2019.
|
| [12] |
杨建雷. 基于非采样Contourlet变换和模糊逻辑的图像增强算法研究[D]. 保定:河北大学, 2011.
|
| [13] |
FRAYSSE A, RODET T . A measure-theoretic variational Bayesian algorithm for large dimensional problems[J]. SIAM Journal on Imaging Sciences, 2013, 7(4).
|
| [14] |
霍冠英, 李庆武, 王敏, 等. Curvelet域贝叶斯估计侧扫声呐图像降斑方法[J]. 仪器仪表学报, 2011, 32(1): 170-177. |
| [15] |
李庆武, 马国翠, 霍冠英, 等. 基于NSCT域边缘检测的侧扫声呐图像分割新方法[J]. 仪器仪表学报, 2013(8): 1795-1801. DOI:10.3969/j.issn.0254-3087.2013.08.016 |
| [16] |
LYU Zhiyu, ZHANG Chengkun, HAN Min. A nonsubsampled countourlet transform based CNN for real image denoising[J]. Signal Processing:Image Communication, 2020, 82. |
| [17] |
LU Huimin, YAMAWAKI A, Serikawa S. Curvelet approach for deep-sea sonar image denoising, contrast enhancement and fusion[J]. Journal of International Council on Electrical Engineering, 2013, 3(3).
|
 2022, Vol. 44
2022, Vol. 44

